多向思维,多种方法,多类拓展*

丘建旺

福建省石狮市华侨中学

有关多变元代数式(特别是双变元)的最值(或取值范围)问题,是高考、竞赛等数学试卷中比较常见的一类题型.此类问题常以函数或方程的形式出现,巧妙融合函数与方程、不等式等基本知识,常考常新,变化多端,难度中等及偏上,具有较好的选拔性与区分度,同时又有一定的技巧方法,是很好考查学生数学基础知识、思想方法与能力的一类创新综合性问题,备受关注.

1 问题呈现

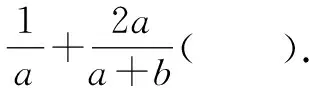
此题以双变元所满足的方程为背景条件,结合分式代数式来确定对应的最值问题.具体破解时,关键是结合题设条件中相应双变元代数式的结构特征,合理联想与巧妙转化,综合逻辑推理与数学运算,并结合相关的知识等,利用代换法、消参法、判别式法以及导数法等常见的基本技巧与方法加以切入与破解.

2 问题破解

思维视角一：基本不等式思维.

解法1：常数代换法.

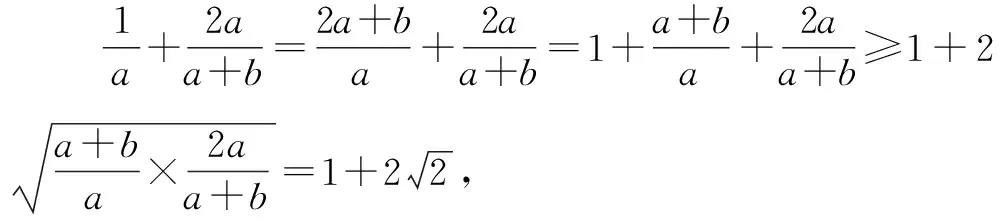
点评：根据题目条件,通过常数“1”的代换,借助所求关系式的恒等变形与转化,利用基本不等式的条件合理配凑,并通过基本不等式来放缩处理.常数“1”的巧妙代入以及关系式的配凑,是破解此类问题的关键所在,也是利用基本不等式确定最值的常用技巧.

解法2：消参法1.

点评：结合题目条件,合理转化,代入所求的代数关系式进行消参处理,进而结合关系式的恒等变形与合理配凑,利用基本不等式来合理放缩应用,进而确定相应代数式的最值.结合条件合理转化,巧妙消参,将双变量代数式问题转化为单变量代数式问题,合理配凑,利用基本不等式来确定最值.

解法3：消参法2.

点评：结合题目条件,合理转化,代入所求的关系式,通过代数关系式的恒等变形与巧妙转化,综合基本不等式的应用条件并通过基本不等式来合理放缩处理.借助基本不等式时的合理配凑,形式多样,变化多端,注意配凑的目的就是使对应的代数式的积为定值,方便利用基本不等式来确定最值.

思维视角二：方程思维.

解法4：判别式法.

点评：根据题目条件,合理转化,代入所求的关系式进行合理消参,巧妙将所求代数式进行整体化处理,进而加以变形转化为二次方程问题.利用方程的判别式法来构建对应的不等式,借助不等式的求解来达到求解最值的目的.构建对应的方程,借助方程思维,通过判别式建立相关的二次不等式,为进一步确定最值提供条件.

思维视角三：函数思维.

解法5：导数法.

点评：根据题目条件,合理转化,代入所求的代数关系式进行消参处理,构建函数,通过求导处理,结合导函数的零点以及函数单调性确定函数的最小值,从而求解相应的最值问题.构建对应的函数,借助函数思维,通过求导处理确定函数的单调性来求解对应代数式的最值问题,是破解一些涉及函数问题的常用技巧方法.

3 变式拓展

保留题目条件,改变原来以选择题形式出现的判断问题为以填空题形式出现的最值题,得到以下更加直接的变式问题.

保留题目条件,改变所求代数关系式中的系数,使得结果更加简捷,可以得到以下相应的变式问题.

当然,变式2中,随着所求代数关系式中系数的适当改变与合理应用,可以得到更多与之相关的变式问题.

4 解后反思

(1)总结方法技巧及其破解策略,形成思维习惯

基于以上问题的分析与解决,我们知道解决此类和定或积定背景下双变元代数式的最值(或取值范围)问题,经常可以通过基本不等式思维、方程思维以及函数思维等来分析与处理,这也是解决此类问题中最为常用的基本思维方式.抓住题设条件中代数式的结构特征,合理选用相应的思维方法,结合与之对应的技巧方法来分析与解决,合理放缩处理,巧妙变形转化,形成解决此类问题的思维习惯.

(2)提升解题技巧及其基本能力,培养学科素养

在实际解决一些数学问题时,要从具体问题入手,从问题背景中展开,挖掘问题的内涵与实质,借助“一题多解”与“一题多思”“一题多用”等方式,深入研究,可以适度展开“一题多变”“多题一解”以及“多类一法”等的应用,从本质上归纳并总结解决相关问题的技巧与方法.

合理根据问题的类型与应用,科学总结解题技巧与策略方法,从而不断提升解题能力,学会举一反三,巧妙融会贯通,全面提升数学能力,培养数学学科核心素养.