一道高考圆锥曲线题的解法探究与反思
高玉立
安微省芜湖市无为县第二中学
高考数学真题是众多优秀命题专家精心设计出来的.其中解析几何压轴题,紧扣教材,立足考查学生的能力.
1 试题呈现

(1)求E的方程;
(2)证明:直线CD过定点.
2 解法探究

思路一:如图1,注意到kPB=3kPA,以及A,B是椭圆的左、右顶点,从而可以借助椭圆第三定义,利用kAC与kAD关系进行求解.

图1
解法1:利用椭圆的第三定义将非对称式转化为对称式问题.
设P(6,t),C(x1,y1),D(x2,y2).

①
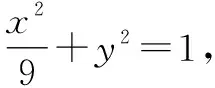
(m2+9)y2+2mny+n2-9=0.
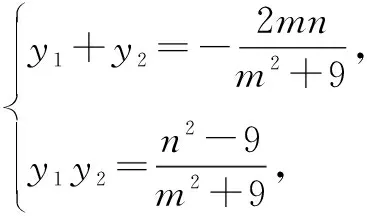
代入①,化简可得2n2+3n-9=0.
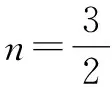
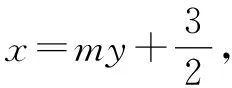
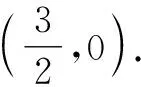
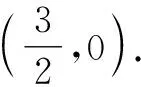
评注:本解法通过椭圆的第三定义巧妙得到直线AC和AD的斜率之积为常数,从而转化为我们熟悉的斜率之积问题.
思路二:如图2,注意到kPB=3kPA,利用椭圆的方程实现斜率的转换,建立kAC与kAD的关系进行求解.

图2
解法2:利用椭圆的方程将非对称式转化为对称式问题.
设P(6,t),C(x1,y1),D(x2,y2).
(ⅰ)若t≠0,设直线CD:x=my+n(-3 ② 3y1y2=-(x1-3)(x2-3). ③ (m2+9)y2+2mny+n2-9=0. 代入③,化简可得2n2+3n-9=0. 评注:本解法通过椭圆的方程,将非对称性韦达定理转化成传统的对称性韦达定理,从而通过基础联立使问题得到解决. 解法3:利用椭圆的方程构造对偶式. 设P(6,t),C(x1,y1),D(x2,y2). (ⅰ)若t≠0,设直线CD:x=my+n(-3 ④ x1y2+3y2=3x2y1-9y1. ⑤ 3x1y2-9y2=x2y1+3y1. ⑥ 评注:本解法通过两次使用椭圆方程得到斜率的两个对称式,真正实现了设而不求,大大简化了计算. 思路四:从题干中的构图顺序,按图索骥,逐个计算出各个点的坐标,从而使问题得到解决. 解法4:从构图顺序逐点计算. 设P(6,t),C(x1,y1),D(x2,y2). (ⅰ)若t≠0,设直线CD:x=my+n(-3 (t2+9)x2+6t2x+9t2-81=0, 评注:本解法依据题干中图形的形成顺序,从直线PA与椭圆方程联立求出点C坐标,再从直线PB与椭圆方程联立求出点D坐标,进而求出直线CD的方程,这种思路更加自然,不足之处是运算量比较大,因此需要学生平常反复训练计算. 对于上述四种思路,前三种思路都是直接从直线CD:x=my+n出发. 思路一利用了椭圆的第三定义kDAkBD=e2-1将非对称式x1y2+3y2=3x2y1-9y1转化成了对称式. 思路四是基于图形的形成顺序,依次算出C,D两点的坐标,然后求出CD的方程,最后算出定点坐标. 四种思路的关联如图3所示: 图3 很多学生之所以认为解析几何问题较难,是因为不会使用题中的条件.因此,教师需要引导学生加强用代数运算的方式解决几何曲线问题这一思想的渗透,用合理的代数方式转化条件中的几何表述,在注重积累的基础上提高条件转化的合理性.比如,本题中通过椭圆定义的使用,将非对称的韦达定理问题转化成对称性的韦达这理问题,从而简化了计算. 数学运算是指在明晰运算对象的基础上,依据法则解决数学问题的素养[1]. 高考试题是为了选拔适合高校并为将来社会服务的人才,因此对计算能力的要求很高.在平常的教学中,要加强学生计算能力的培养,让学生在遇到复杂运算时不畏惧并保持高度的细心,这也是今后从事科研工作所不可或缺的品质. 这类非对称的定点与定值问题,其实并不是全新的问题,这就要求我们在日常教学中对于一些典型性问题要精编精整理,以微专题的形式实现知识方法的串联、整合,由易到难,层次分明,循序渐进,力求贴近学生的知识经验和能力基础,贴近学生的情感态度与思维水平,使得学生的技能水平自然而然得到提高. 高考是选拔性考试,是为了给高等学校尤其是高水平大学挑选合适的人才.我们的数学教学也要培养学生的思维能力,能够创新性地解决问题.通过对一道题的多角度、多方法的思考,不断提升数学学科素养,以适应时代发展的要求. 当然,本题也涉及到极点、极线的背景,对于一些学有余力的学生,在日常教学中也不妨给他们适当补充点课外知识,激发他们的兴趣.教师要让学生尽可能完成“跳一跳”可以完成的任务[2].总之,这道高考题内容丰富,解法多样,立足基础,又能充分发挥学生的创新性,让人回味无穷,实在是一道好题!
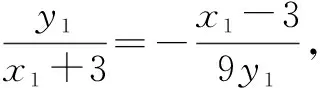
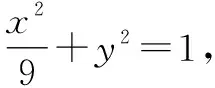
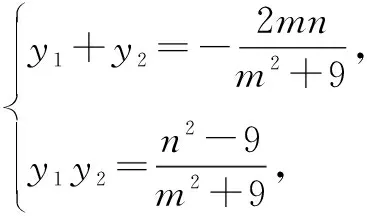
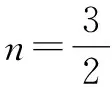
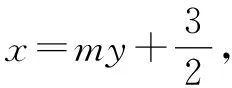
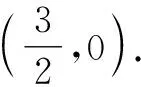
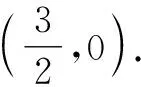
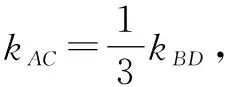





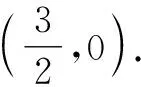
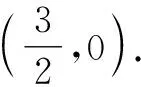

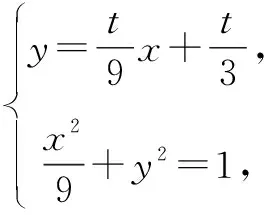


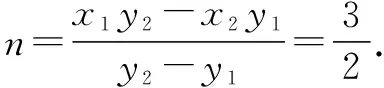
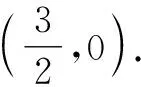
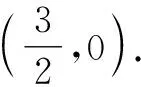
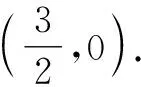
3 思路总结
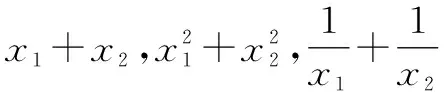
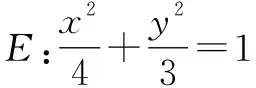
4 解后反思
4.1 注意条件的转化
4.2 注重计算能力的训练
4.3 注重微专题的变式精讲
4.4 注重学生思维能力的培养,适应新高考要求

