发挥学生主体作用,助推学生深度学习——以“等比数列的前n项和”的教学设计为例

韩雪梅

山东省济南市莱芜第一中学

目前,数学教学中依然存在着程序化、形式化、碎片化的浅层学习方式,影响了学生学习能力的提升和思维能力的发展.为了帮助学生获得更好的学习效果,数学课堂上需要对数学知识的深度学习,以此提高学生学习层次,强化学生学习能力,建构知识体系,让学生获得可持续学习能力,促进终身学习目标的达成[1].笔者以“等比数列的前n项和”教学为例,谈谈自己对深度学习的一些认识,供参考.

1 教学过程

1.1 联系旧知,明晰方向

问题1回顾已学的等差数列和等比数列的相关知识,完成表1.

表1

设计意图：引导学生回顾已学知识,以期通过新旧知识的有机融合让学生对数学知识的理解更加系统化、结构化,培养学生良好的思维习惯.

1.2 创设情境,让学引思

问题2为了让全世界(约75亿人)的人都能了解南京,南京某校欲开展“信息传递”活动.小明作为第1天的“传递官”需要将南京的人文历史介绍给两个人.第2天包括小明在内就有3人知道信息了,两名新的“传递官”将之前获得的信息分别传递给两个人,这样第3天就有7人得知信息,以此类推,多少天后能够实现目标呢?请尝试用数学语言表述.

问题给出后,学生积极思考,很快就有了发现.

生1:第1天1人,第2天新增2人,第3天新增22人,第4天新增23人,……,第n天新增2n-1人,问题可以转化为不等式问题,即求1+2+22+……+2n-1≥7.5×109.

师:分析得很有道理,不过这个不等式该如何求解呢?(学生陷入沉思)

师:64天后会有多少人知道呢?S64=1+2+22+23+……+263=?

问题给出后,让学生分组探索求解方法.在教师的启发和引导下,学生给出了如下解法:

解法1：错位相减.

S64=1+2+22+23+……+263,

①

2S64=2+22+23+……+263+264.

②

②-①,得S64=264-1.

解法2：猜测归纳.

S1=1=21-1,S2=3=22-1,S3=7=23-1,……,猜测S64=264-1.

解法3：内部结构分析.

S64=1+2+22+23+…+263

=1+2(1+2+22+23+…+262)

=1+2S63,

所以S64=1+2(S64-263).

故S64=264-1.

设计意图：活动与体验是发展学生学习能力、提升学生数学素养的重要途径.教学中,教师以贴近学生的生活情境为背景,引导学生用数学语言去表述,用数学思维去思考,提高学生数学能力.在问题的解决过程中,教师没有直接呈现问题分析和解决的过程,而是放手让学生去思考、去合作,鼓励学生从不同角度探寻解决问题的方法,以此提高思维活力,引发深度学习[2].

1.3 公式推导,揭示本质

问题3如果将推导等比数列前n项和公式转化为一道数学题,可以怎样转化呢?

生2:已知等比数列{an}的首项为a1,公比q(q≠1),记Sn=a1+a2+a3+……+an,求Sn=f(n)(n∈N*)的解析式.

问题4请结合探索“S64=1+2+22+……+263=?”的经验,求Sn=f(n)(n∈N*)的解析式.

问题给出后,预留充足的时间让学生思考.通过积极思考与交流,学生给出了如下推导过程:

证法1：当q≠1时,

Sn=a1+a2+a3+……+an+0,

③

qSn=0+a2+a3+……+an+an+1.

④

③-④,得(1-q)Sn=a1-qan=a1-a1qn.

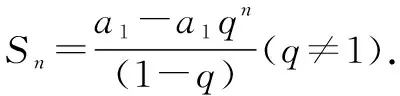
证法2：当q≠1时,

因为Sn=a1+a2+a3+……+an

=a1+q(a1+a2+a3+……+an-1)

=a1+qSn-1,

所以Sn=a1+q(Sn-an).

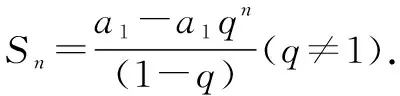
问题5当q=1时,如何求等比数列的前n项和?请写出等比数列的前n项和公式.

学生归纳总结,得到等比数列的前n项和公式:

设计意图：公式推导是本节课的重难点内容,是诱发深度思考的重要途径.在本课教学中,教师一改往日以师为主的讲授模式,引导学生通过小组合作自主推导公式,以此通过经历公式推导的过程,理解公式的本质属性.在以上教学过程中,引导学生用精准的数学形式进行问题的表征,用不同的方法证明,让学生体验了等比数列前n项和的本质,为后期应用打下了坚实的基础.同时,不同角度的证明方式,拓宽了学生的视野,实现了数学思维的进阶.

1.4 公式应用,提高能力

问题6回归最初的问题2,按照以上传递方式,多少天后可以让全世界的人认识人文荟萃的南京呢?

学生根据公式求解:2n-1≥7.5×109,所以n≥log2(7.5×109+1)≈32.8,故33天后可以完成.

问题解决后,教师又给出例题帮助学生巩固强化,题目如下:

例1判断下列各式中公式的使用是否正确?若不正确,请给出理由.

例2已知数列{an}是等比数列,首项为a1,公比为q,Sn为数列{an}的前n项的和.

(1)若a1=1,ak=243,q=3,求Sk;

设计意图：例题是课堂教学的重要组成部分,通过问题的解决既能达到巩固强化的目的,又能帮助学生积累丰富的解题经验.教师设计以上题目旨在引导学生辨析公式的本质属性,加强公式理解的深度,进一步提高学生数学抽象素养.

2 教学思考

在高中数学教学中,教师要打破传统的“讲授+题海”,提供机会让学生去思考、去探索、去交流,以此通过亲身经历逐步培养“四基”、落实“四能”.为了实现这一目标,教师在教学设计中应注意以下几点:

2.1 重视突破重难点

公式的推导是本课教学的重点,也是难点.为了凸显重点、突破难点,教师没有直接将教材中的推导过程呈现给学生,而是让学生结合已有的知识和能力寻找适合的推导方法,以此激发学生探究兴趣,让学生更加全面、深刻地理解公式.推导公式时,学生给出了3种不同的推导方案,获得了对公式不同角度的理解,充分展示了思维的创新性,提高了自身的思维品质.

2.2 重视公式本质的理解

数学公式具有高度的抽象性,教学中需要引导亲身经历数学公式抽象的过程,以此帮助学生把握数学公式的本质.本课教学中,教师将公式推导的主动权交给学生,学生得到了不同的推导方案,对数学公式获得了本质的理解.

总之,数学教学中,教师要认真研究教学内容,认真研究学生,结合教学实际创设有效的问题,让学生在问题的驱动下积极思考、积极合作,通过深度学习加深学生对数学本质的理解,提升教学品质.