关于n-纯同调维数的注记
吕家凤, 金欣怡
(1.浙江师范大学 数学科学学院,浙江 金华 321004;2.浙江师范大学 初阳学院,浙江 金华 321004)
0 引 言
自20世纪六七十年代纯模与纯正合列的概念提出后,其性质引起了广泛关注.值得注意的是,纯正合列的定义是基于有限表现模的.为了研究诺特环、凝聚环以及更一般环上的同调性质,模的有限表现性的研究越来越受到人们的关注[1-5].例如,Bravo等[4]建立了n-凝聚环与n-表现模之间的联系,并研究了其同调性质.设n为非负整数,如果存在一个正合列Pn→Pn-1→…→P1→P0→M→0,使得每个Pi都是有限生成的投射模,那么称一个模M为n-表现的[2].易见,0-表现模是有限生成的,1-表现模即为有限表现模,每个(n+1)-表现模是n-表现的.反之不成立,文献[3]给出了反例.最近,为了研究n-纯导出范畴的同调性质,文献[5]引入了n-纯正合列、n-纯投射模以及n-纯内射模等概念.受此启发,本文运用同调的方法,研究了模与环的n-纯投射维数与n-纯内射维数,并证明了环R的n-纯投射整体维数不超过1的充分必要条件是R的n-纯内射整体维数不超过1.
本文中,环R指的是含单位元的结合环,除特别说明外,R-模表示的是左R-模,m与n均为非负整数.其他未说明的概念与术语参见文献[6-8].
1 预备知识
定义1若对任意n-表现模M,有正合列
0→HomR(M,A)→HomR(M,B)→HomR(M,C)→0,
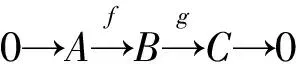
定义2设M为R-模,若对任意n-纯正合列0→A→B→C→0,都有正合列
0→HomR(M,A)→HomR(M,B)→HomR(M,C)→0,
则称M为n-纯投射模.类似地,若对任意n-纯正合列0→A→B→C→0,都有正合列
0→HomR(C,M)→HomR(B,M)→HomR(A,M)→0,
则称M为n-纯内射模.
以下分别用PPn与PIn表示所有n-纯投射模与n-纯内射模.
命题1[5]设η:0→A→B→C→0为R-模正合列,则下列条件等价:
1)η是n-纯正合列;
2)对任意n-纯投射模P,有正合列
0→HomR(P,A)→HomR(P,B)→HomR(P,C)→0;
3)对任意n-纯内射模E,有正合列
0→HomR(C,E)→HomR(B,E)→HomR(A,E)→0.
设X为由一些R-模组成的类,M为R-模.M的X-预覆盖[7]是指一个模同态φ:X→M,其中X∈X,并且对任意的X′∈X,HomR(X′,φ):HomR(X′,X)→HomR(X′,M)都是满同态.若φ:X→M是M的一个X-预覆盖且满足φg=φ的自同态g:X→X只能是X的自同构,则称φ为M的X-覆盖.如果对于任意的R-模,它的X-(预)覆盖都存在,那么称X是(预)覆盖类[7].对偶地,可定义X-预包络、X-包络以及X是(预)包络类等概念.
命题2[5]设R为环,则下列结论成立:
1)PPn与PIn均对直和项封闭;
2)PPn是预覆盖类;
3)PIn是包络类.
设M是非零R-模,M的n-纯投射分解是指一个n-纯正合列
其中,P0,P1,P2,…都是n-纯投射模.
由于PPn是预覆盖类,所以每个模都有PPn投射分解.
定义3若M有长度为m(0≤m< ∞)的n-纯投射分解
则称M的n-纯投射分解的最小长度为M的n-纯投射维数;若M没有长度有限的n-纯投射分解,则M的n-纯投射维数定义为∞.通常用PPn-pdR(M)表示M的n-纯投射维数.所有R-模的n-纯投射维数的上确界称为环R的n-纯投射整体维数,记作PPn-PD(R),即
PPn-PD(R)=sup{PPn-pdR(M)|M为任意R-模}.
对偶地,M的n-纯内射分解是指一个n-纯正合列
使得E0,E1,E2,…都是n-纯内射模.
由于PIn是包络类,所以每个模都有n-纯内射分解.
定义4若M有长度为m(0≤m<∞)的n-纯内射分解
则称M的n-纯内射分解的最小长度为M的n-纯内射维数;若M没有长度有限的n-纯内射分解,则M的n-纯内射维数定义为∞.通常用PIn-idR(M)表示M的n-纯内射维数.称所有R-模的n-纯内射维数的上确界为环R的n-纯内射整体维数,记作PIn-ID(R),即
PIn-ID(R)=sup{PIn-idR(M)|M为任意R-模}.
2 主要结论
主要结果如下:
定理1设R为环,则下列叙述等价:
1)LPPn-PD(R)≤1;
2)LPIn-ID(R)≤1;
3)对M的每个n-纯投射分解
都有Ker(f)∈PPn;
4)对M的每个n-纯内射分解
都有Coker(g)∈PIn.
首先,讨论模M的n-纯投射维数与n-纯内射维数.
引理1设M为R-模且m为非负整数,则下列叙述等价:
1)PPn-pdR(M)≤m;
2)对M的每个n-纯投射分解
都有Ker(∂n-1)∈PPn.

于是有下面的行与列均是正合的交换图:

因为0→Ker(f)→P0→M→0是n-纯正合的,所以由命题1知,0→Ker(f)→X→Q0→0也是n-纯正合的.由于Q0是n-纯投射模,从而0→Ker(f)→X→Q0→0是可裂的,所以X≅Ker(f)⊕Q0.类似可证明X≅Ker(g)⊕P0.由此可知,Ker(f)⊕Q0≅Ker(g)⊕P0.由Ker(g)存在长度为s的n-纯投射分解可知,PPn-pdR(Ker(g))≤s.因此,PPn-pdR(Ker(f))≤s.故由归纳假设可知,Ker(∂n-1)∈PPn.引理1证毕.
对偶地,易得下述引理:
引理2设M为R-模且m为非负整数,则下列叙述等价:
1)PIn-idR(M)≤m;
2)对M的每个n-纯内射分解
都有Coker(∂m+1)∈PIn.
引理3设M为左R-模,则下列叙述等价:
1)M是n-纯投射模;
2)对任意n-纯正合列0→K→E→F→0,其中E是n-纯内射模,都有正合列
0→HomR(M,K)→HomR(M,E)→HomR(M,F)→0.
证明1)⟹2)显然成立,只需证明2)⟹1).设0→A→B→C→0是n-纯正合列.由命题2知,存在n-纯正合列0→B→E→K→0,其中E是n-纯内射模.于是有下面的行与列均是正合的交换图:
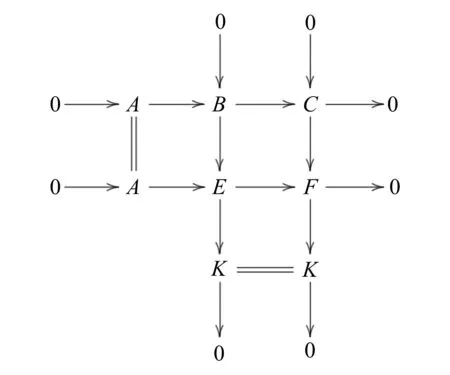
因为0→A→B→C→0与0→B→E→K→0均是n-纯正合的,所以0→A→E→F→0也是n-纯正合的.由2)知,0→HomR(M,A)→HomR(M,E)→HomR(M,F)→0与0→HomR(M,B)→HomR(M,E)→HomR(M,K)→0均为正合列.用函子HomR(M,-)作用上述交换图可得下面的交换图:
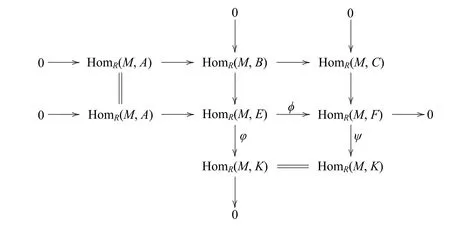
由于φ=ψφ是满同态,从而ψ也是满同态,所以由3×3引理可知,0→HomR(M,A)→HomR(M,B)→HomR(M,C)→0是正合列.因此,M是n-纯投射模.引理3证毕.
对偶地,有下述引理:
引理4设N为左R-模,则下列叙述等价:
1)N是n-纯内射模;
2)对任意n-纯正合列0→K→P→L→0,其中P是n-纯投射模,都有正合列
0→HomR(L,N)→HomR(P,N)→HomR(K,N)→0.
定理1的证明1)⟸⟹3)由引理1可得.2)⟸⟹4)由引理2可得.
3 结 语
本研究是基于前人的成果下,运用同调方法,通过探讨n-纯投射模与n-纯内射模的一些同调性质,给出了模的n-纯投射维数与n-纯内射维数的一些刻画,并证明了环R的n-纯投射整体维数不超过1的充分必要条件是R的n-纯内射整体维数不超过1.在本研究的基础上,将来还可以进一步探讨环R的高维n-纯投射整体维数与高维n-纯内射整体维数之间的关系.

