求解分裂可行问题的次梯度投影松弛算法
陈进作, 王元恒
(浙江师范大学 数学科学学院,浙江 金华 321004)
0 引 言
分裂可行问题[1]自提出以来,得到越来越多学者的关注[2-8],并且在信息[2]、医疗[3]等领域得到了广泛应用.分裂可行问题的数学模型是
寻找x∈C使得Ax∈Q.
(1)
式(1)中:C,Q分别为Hilbert空间H1与H2的非空闭凸集;A是有界线性算子.Byrne[3]提出CQ算法,
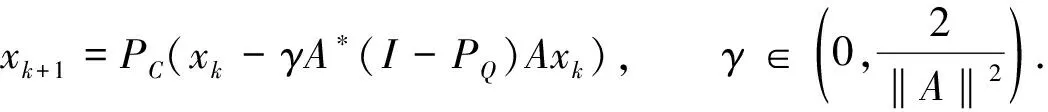
(2)
式(2)中:PC是空间H1在C上的投影算子;PQ是空间H2在Q上的投影算子;I是恒等算子.后续的算法研究多数是在CQ算法基础上的完善与改进,其中有较大影响的是Yang[4]提出的建立在半空间上的松弛CQ算法,
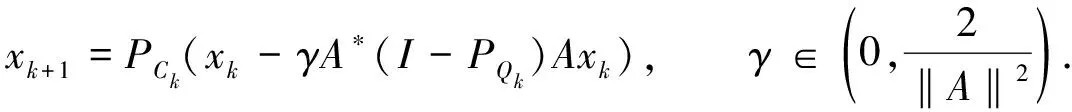
(3)
式(3)中:Ck是C与一族半空间的交集;Qk是Q与一族半空间的交集.相对非空闭凸集C与Q,半空间上投影的计算更加简单.注意到CQ算法(2)与松弛CQ算法(3)中的步长依赖于算子范数‖A‖,Lpez等[5]提出自适应步长,改进了松弛CQ算法,
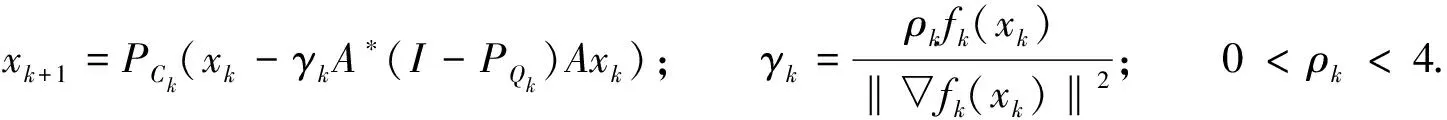
(4)
注意到算法(2)~算法(4)中的投影都是正交投影,本文提出次梯度投影算法求解分裂可行问题.
1 预备知识
定义次梯度投影,需要以下概念及命题:
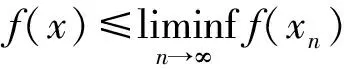
定义2[10]水平集C0={x∈H1|c(x)≤0},其中c:H1→(-∞,+∞]为下半连续凸函数;水平集Q0={y∈H2|q(y)≤0},其中q:H2→(-∞,+∞]为下半连续凸函数.
定义3[10]给定函数f:H1→(-∞,+∞],当
f(y)≥f(x)+〈u,y-x〉,y∈H1
成立时,称u为f在点x的次梯度.称f在点x的所有次梯度构成的集合为f在点x的次微分,记为∂f(x).
定义4[10]设H为Hilbert空间,给定水平集C0,给定函数f:H→R,取定s(x)∈∂f(x),定义关于函数f的次梯度投影为:
G:H→H;

如果f为Gateaux可微,那么关于f的次梯度投影为:
G:H→H;
引理1[6]给定函数f:H1→(-∞,+∞],则f为下半连续凸函数当且仅当f为弱下半连续凸函数.
定义5[8]给定H1中非空闭凸集C,若{xk}⊂C,则当
‖xk+1-z‖≤‖xk-z‖, ∀z∈C
成立时,称{xk}是Fejer单调的.
引理2[7]若{xk}在C中是Fejer单调的,则{xk}弱收敛于z∈C当且仅当{xk}的每一个弱聚点都在C中.
性质1[7]设H为Hilbert空间,Fix(T)为T的不动点集,给定非线性算子T:H→H,若〈Tx-x*,Tx-x〉≤0,x∈H,x*∈Fix(T),则称T具有cutter性质.
2 主要结果
接下来引入次梯度投影松弛算法来解决分裂可行问题(1).假设问题(1)是有解的,解集为Γ;假设问题(1)中的C与Q分别定义为水平集C0与Q0,它们由定义2给出;对任意x∈H1,假设至少存在1个φ∈∂c(x),对任意y∈H2,假设至少存在1个φ∈∂q(y);假设∂c(x)与∂q(y)在有界集上是有界的[10].
定义半空间
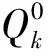
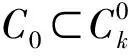
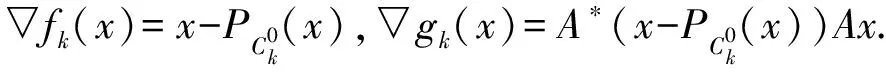
Gfk:H1→H1;
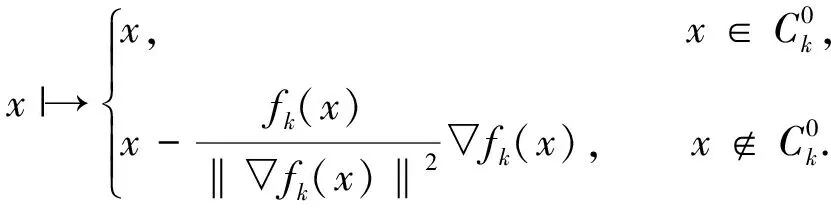
定义关于gk的次梯度投影为:
Ggk:H2→H2;

记Rμkfk=I+μk(Gfk-I),Rλkgk=I+λk(Ggk-I),通过Rμkfk与Rλkgk构造次梯度投影松弛算法,
xk+1=Rμkfk∘Rλkgk(xk),k≥1.
(5)
定理1设序列{xk}由算法(5)迭代生成,当μk∈(0,2),λk∈(0,2)时,序列{xk}弱收敛于分裂可行问题(1)的解.
证明第1步,证明Ggk和Gfk具有cutter性质.
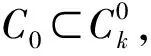
下面证明Ggk具有cutter性质.
〈Ggk(xk)-τ,Ggk(xk)-xk〉≤0,
(6)
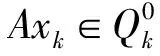
〈Ggk(xk)-τ,Ggk(xk)-xk〉=〈Ggk(xk)-τ,xk-xk〉=0;
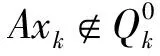
〈Ggk(xk)-τ,Ggk(xk)-xk〉=
综上所述,式(6)成立.记wk=Rλkgk(xk),同理可得
〈Gfk(wk)-τ,Gfk(wk)-wk〉≤0.
(7)
第2步,证明序列{xk}关于Γ是Fejer单调的.
由式(6)得
‖wk-τ‖2=
‖xk-τ‖2-λk(2-λk)‖Ggk(xk)-xk‖2.
由式(5)与式(7)得
‖xk+1-τ‖2=
‖xk-τ‖2-λk(2-λk)‖Ggk(xk)-xk‖2-μk(2-μk)‖Gfk(wk)-wk‖2≤
‖xk-τ‖2.
(8)
由假设μk∈(0,2),λk∈(0,2)得序列{xk}关于Γ是Fejer单调的,故序列{xk}是有界的.
第3步,证明Ax*∈Q0.
由式(8)得
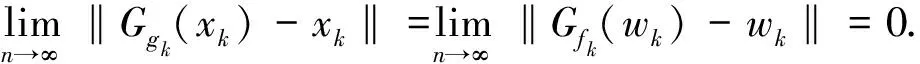
(9)
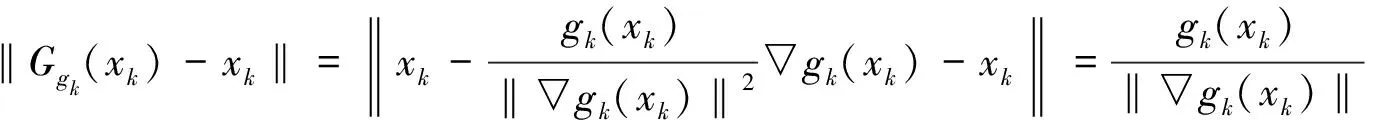
‖▽gk(xk)‖=‖▽gk(xk)-▽gk(τ)‖≤‖A‖2‖xk-τ‖,
(10)
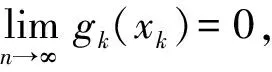
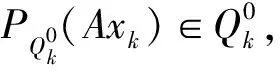
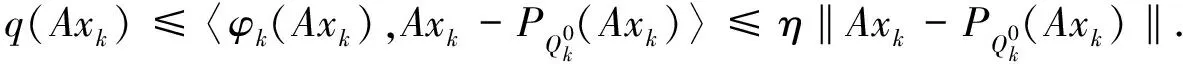
(11)
因为函数q是凸的且下半连续,所以由引理1得q是弱下半连续的.由式(11)得
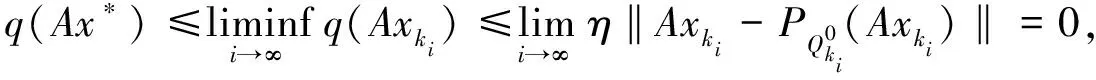
(12)
这说明Ax*∈Q0.
第4步,证明x*∈C0.
由wk=Rλkgk(xk)及式(9)得

(13)
这说明{wki}弱收敛于x*.下面证明x*∈C0.
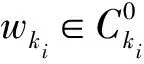
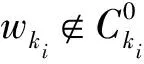
再由式(11)~式(13)得c(x*)≤0,即x*∈C0.
最后,由引理2得序列{xk}弱收敛于x*,从而说明x*是分裂可行问题(1)的解.定理1证毕.
3 结 语
在无限维Hilbert空间中,利用次梯度投影技巧,提出求解分裂可行问题的松弛算法,并证明算法生成的序列收敛于分裂可行问题的解.
定理1的证明分为4步.第1步,采用分类讨论的数学思想证明了次梯度投影算子的cutter性质; 第2步,根据cutter性质,证明了关于gk与fk的复合次梯度投影松弛算法生成的序列具有Fejer单调性,从而说明序列的有界性;第3步,证明了Ax*∈Q0;最后一步,采用分类讨论的思想证明了x*∈C0,从而说明x*是分裂可行问题(1)的解.
CQ算法(2)、松弛CQ算法(3)和改进的松弛CQ算法(4)中的投影都是正交投影,本文使用的是由次梯度投影构造的算法来求解分裂可行问题.本文给出的算法迭代收敛于问题(1)解的方法及证明过程与上述算法有所不同.

