爬缆机器人运动规划的几何优化方法
徐滨
(合肥职业技术学院 机电工程学院,安徽 合肥 230012)
软体机器人主要由杨氏模量较低的材料组成,应用于众多领域,例如机器人辅助微创手术、激光导航等[1-3]。利用机器人按照指定的规划路径进行轨迹跟踪是最常见的一种应用场景,在实践中也取得了很好的效果,但对于软体机器人的轨迹跟踪来说仍然存在许多挑战,如软材料的弹性、特殊的驱动方式等。对于电缆驱动的软体机器人,需要至少3根驱动缆索才能实现空间的可操作性,通常采用几何推导的分段常数曲率方法来获得建模的闭合解[4-7]。
本文通过观察由驱动和段之间的耦合效应引起的被动轴向压缩现象,推导出一个线性的多段缆索驱动机器人运动学模型。传统的分段常数曲率方法为连续体机器人的模型控制提供了基础框架,但对于缆索驱动的连续体机器人,其适用性不够好,尤其是应用在弯曲的多个缆索驱动时,将不可避免地引入轴向压缩和耦合问题。为此,本文考虑了上述条件的任务空间,提供了更高的精度,并开发了多段缆索驱动机器人模拟器来验证机器人在不同约束条件下的性能,包括固定末端的轨迹跟踪方向、在末端轨迹跟踪过程中避开障碍物等。
1 可压缩曲率模型
利用文献[4]中的分段常数曲率模型,对于具有N段的多段软体机器人,其第k个段(k≤N) 可以在配置空间中通过ψk=[θk,φk,κk]T进行几何参数化,其中,θk∈[0,θmax]表示弯曲角度,φk∈[-π、π)表示弯曲方向的角度,κk是与段Lk的初始未变形长度相关的弯曲曲率,且κk=θk/Lk。因此,第k段相对于基础框架∑k-1的位置可以表示为
(1)
如图1所示,第k个段ψk的配置可由电缆驱动推导如下:
(2)
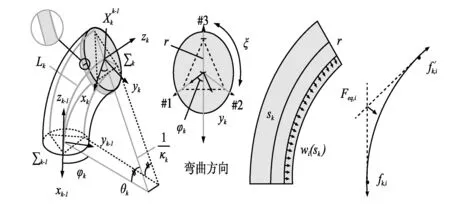
图1 缆索驱动软体机器人示意,深色部分表示轴向压缩
(3)
(4)
式中:r为横截面中心和电缆通道之间的对称距离(常量);qk,i⊆qk为第k段第i根缆索长度的驱动,通过用体内缆索长度Lk,i减去中性线Lk的长度得到
qk,i=Lk,i-Lk=-θkrcos(φk+(i-1)ξ)
(5)
式中:i∈{1,2,3};ξ=2π。
对于n段耦合在一起的多段软机器人,由于累积张力,其(k-1)段的轴向应变比k段大。假设第k段缆索的拉力为fk=[fk,1,fk,2,fk,3]T,当缆索被驱动并处于平衡状态时,候选函数fk:Q3→R3可以将关节变量映射为满足所有qk,i∈Q3准静态平衡的力向量,其表示为
(6)
在准静态状态下,如图1所示,可以得到单根缆索的静力平衡方程:
(7)

(8)
式中:Kb=EI为结构的抗弯刚度;Μk=|τk|为第k段的局部弯矩;Мk为受可变长度影响的第k段的弯矩。段压缩会导致局部弯曲刚度变化,越靠近底座越硬。因此,对于带有耦合电缆的多段软机器人,如果不是最末端的段,则每个段的局部弯曲刚度应不同且相关。本文没有单独确定局部弯曲刚度,而是制定了响应轴向压缩的可变刚度。式(8)表明,轴向压缩不仅会影响末端的定位效果,还会影响到实际应用中逆解的推导。
2 机器人描述
本文利用两段式的缆索驱动软体机器人作为原型来进行方法验证,且安装了3个带驱动电缆的伺服电机(偏移量ζ为180°)。机械手垂直安装在线性滑块上,形成插入-收缩的组合运动,记为q0,且q0≥0。因此,执行器空间可表示为
q=[q0q1,1q1,2q1,3q2,1q2,2q2,3]T
(9)
式中:qc∶=[q1,1q1,2q1,3q2,1q2,2q2,3]T定义为电缆驱动。使用的电缆材料是编织鱼线,其在轴向上相对坚硬(最大拉力为30 kg)。假设在所选伺服电机的驱动下,它们不可拉伸,最大扭矩为10 N·m。因此,电缆的张力可以类似地定向为电机驱动。末端关于空间固定世界框架∑0的齐次变换矩阵可表示为
(10)
式中:H=[0,0,q0]T为滑动运动。
3 基于优化的轨迹跟踪约束运动规划
(11)
式中:J(q)∈3×7为推断冗余机器人的雅可比矩阵;(·)†为右伪逆算子,即JT(JJT)-1。第二项将的分量投影到J的零空间,I是一个7×7的单位矩阵。每次更新雅可比矩阵时,末端位置在无限短时间内的变化Δx可以根据驱动的变化Δq进行近似计算,使得Δq=J†Δx。
由于系统冗余,上述等式可能存在无穷解,可以通过一些数值方法来解决。例如基于雅可比矩阵的满秩伪逆方法J(q)来求解机器人的逆运动学;或利用最小阻尼-平方逆方法,可以通过正确选择阻尼参数λ来避免奇点,并提供了一种选择Δq的数值稳定策略。为了获取达到理想路径χd所需的驱动q,该方法通过求解一个凸最小二乘优化问题来计算逆运动学:
(12)
式中:λ∈>0为非零的阻尼常数。这个二次优化问题通过最小化生成的末端位置和期望的末端位置之间的误差,同时考虑到驱动空间中可行的最小运动问题,从而生成满足末端路径跟踪要求的解Δq。此外,通过式(11)中介绍的零空间来包含更多的子目标,以满足环境和机器人上所施加的不同约束。
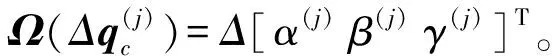
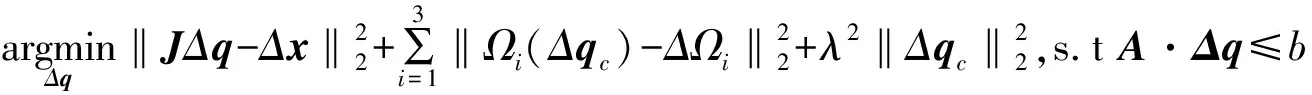
(13)
其中,A=diag(10-3,1,1,1,1,1,1),b=(0.01) ×7,这两个变量都分别定义了线性不等式的约束。Ωi表示列向量的第i行,ΔΩi是末端方向预期的变化量。基于机器人末端的工作区域,有界条件分别设置为qmin=-[0,2,2,2,2,2,2]T,qmax=[60,0,0,0,0,0,0]T。
与式(12)相比,式(13)中的附加项在线性不等式和有界条件的约束下,可以最小化生成的任务空间方向变化与期望的任务空间方向变化之间的误差。
4 实验验证与分析
4.1 模型验证
使用改进的可压缩曲率模型的两段式缆索驱动机器人,其基本弯曲运动如图2所示,其中图2a 为只有近段弯曲;图2b为只有远段弯曲;图2c为两个段均有弯曲,但近段弯曲补偿了远段弯曲;图2d为两段都朝着同一方向弯曲。由图2可看出,由于耦合效应,驱动的远端节段将导致近端节段被动弯曲。
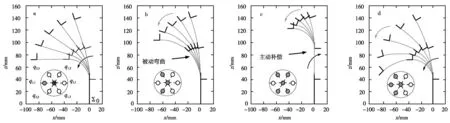
图2 两段缆索驱动机器人的耦合效应
本文对软段上的可压缩曲率模型进行了实验验证,首先在缆索驱动机器人的近段上进行平面弯曲试验。由于材料柔软,当驱动电缆时,管段将承受轴向压缩。这里使用了一个不可伸缩的分段常数曲率模型,该模型排除了机器人运动时弧长的变化,即sk(f≠0)=Lk。如图3所示,组1和组2分别表示总弧长为98,96 mm。

图3 在软机器人上验证可压缩曲率模型
由图3可知,一般连续体机器人的不可伸缩分段常数曲率模型对于软体机器人来说不够友好。然而,本文提出的可压缩曲率模型可以更好地预测在给定驱动输入下的末端位置。
4.2 约束运动规划
由于施加在不可伸缩缆索上的拉力可以视为缆索的位移,先通过实验测量施加的拉力和缆索位移之间的比例,即qc=μf,其中μ=18 mm/N,为基于调谐的缆索张力。为了给电机产生平滑的输入,使用移动中值滤波器来减少其中的周期性趋势和异常值。接着对固定方向约束下的轨迹跟踪性能进行了测试。使用时间步长的参数化函数来表示运动轨迹,验证了计算得到的输入能够产生预期的受约束机械手运动,并且达到了满意的精度水平。
图4显示了末端执行器对末端方向垂直于地面的椭圆形的跟踪结果。图5显示了在相同路径下为缆索驱动机器人分配20°倾斜角时,椭圆形的跟踪情况。

a 不同时间下位置误差和方向误差 b 整体跟踪性能 a 不同时间下位置误差和方向误差 b 整体跟踪性能
由图4可知,通过目视测量得出,轴向误差在2 mm以内,方向误差在10°以内。由图5可知,由于机械手试图在跟踪过程中弯曲自身以保持特定的末端方向,尽管椭圆路径长端的定位精度不如垂直情况下的定位精度,但最终结果还是满足了固定方向的要求。
5 结语
本文提出了一种结合可压缩曲率建模的方法,用于分段耦合效应下的多段缆索驱动软机器人的运动规划。机器人建模主要解决由弹性材料和缆索驱动结构导致的段缩短现象。基于缆索和柔体的力学原理,推导了执行器空间、构形空间和任务空间之间的解耦映射。在此基础上,设计了一种基于几何优化的运动规划算法,以扩展冗余度软机器人在约束条件下的可控性,包括使用固定方向的末端轨迹跟踪执行器和操纵器来避免障碍物碰撞。基于一个两段式的机器人原型进行了数值仿真实验,验证和评估所提出的末端轨迹跟踪算法。该方法可以推广到约束条件下任意的多段缆索驱动软机器人运动规划。

