高后坐过载下硅基MEMS后坐保险装置响应特性

强 甲,赵 旭,田中旺,王晓霞

(西安机电信息技术研究所,陕西 西安 710065)

0 引言

随着高新科技武器的不断发展,引信的功能需求也越来越多,对于引信体积使用率也有了更高的要求。微机电系统(MEMS)[1-2]具备微小型化、低功耗、多功能、高集成等特点,与引信小型化和智能化的需求十分吻合。MEMS安全系统[3-4]是采用MEMS加工技术实现引信的安全系统功能,硅基MEMS的集成通过微系统封装工艺实现,可以与微电子一体化加工,应用前景广阔。MEMS后坐保险装置作为MEMS安全系统的一个功能部件,用来感知发射环境,解除第一道保险。但硅材料弹性相较于金属基材料,延展性不足;硅基后坐保险装置集成后,在上万g的过载环境下,很容易发生失效。研究高后坐过载环境下硅基后坐保险装置的响应特性,可以为硅基结构设计优化提供支撑。

MEMS后坐保险装置最初由Charles H. Robinson团队[5-8]于1998年在其专利中提出,通过几代改进设计已较为成熟。近些年国内对于后坐保险装置进行了大量研究,南京理工大学团队着重对悬臂梁结构MEMS后坐保险装置进行分析,文献[9-11]将悬臂梁等效为弹簧质量块系统,并推导出MEMS后坐保险装置最大响应位移与固有角频率之间的关系;文献[12]研究了影响固有角频率的结构因素和固有角频率之间的关系;文献[13]通过瑞利商法计算固有角频率并完整预测了后坐保险机构在冲击载荷下的位移时间过程曲线;文献[14]建立了闭锁机构可靠闭锁的临界阈值能量模型并进行了试验验证;文献[15-16]对MEMS后坐保险装置进行了马歇特锤击性能测试。针对垂直基板式MEMS后坐保险装置,文献[17]建立了影响MEMS后坐保险装置后坐加速度的表达式,得到了相关因素与加速度的关系,并采用离心机对MEMS后坐保险机构进行解除保险性能试验,通过观察试验结果验证了方程和仿真的合理性;文献[18]对MEMS后坐保险装置进行了正常发射和跌落两种环境的失效模式仿真,并进行了锤击试验验证;文献[19]对齿形制动的硅基后坐保险装置进行了仿真研究,完善了质量块位移响应计算公式。综上可知,目前国内的设计主要集中在镍基方面,技术已较为成熟,但对于硅基MEMS后坐保险装置的研究主要集中在理论分析和仿真研究,基于目前资料,尚不能解决垂直基板式硅基MEMS后坐保险装置高后坐过载下响应特性问题。

本文提出了一种硅基后坐保险装置,对其进行了理论模型分析,勤务跌落和发射环境动力学仿真和试验测试,研究了其失效形式,并提出了一种优化方案,为该装置的进一步改进提供理论支撑。

1 MEMS安全系统工作原理

本文研究的对象为垂直基板式后坐保险装置,根据GJB 373B-2019《引信安全性设计准则》要求,其组成框图如图1所示,主要由后坐保险装置、离心保险装置、指令锁机构和隔爆滑块等组成。

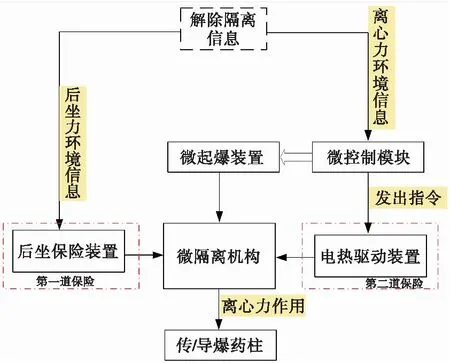
图1 硅基MEMS安全系统组成框图Fig.1 Silicon based MEMS security block diagram

其工作原理:当弹药发射时,后坐保险装置在后坐力的作用下,质量块运动至闭锁机构并闭锁,解除微隔离机构的第一道保险;到达设定延期解除隔离距离,微控制模块发出指令,电热驱动装置逐步释放隔爆滑块,达到延期解除隔离的作用,微隔离机构在离心力作用下运动到闭锁机构并闭锁,此时传爆序列对正,引信处于待发状态。

2 理论模型

后坐保险装置主要由基板、质量块、弹簧及闭锁机构构成,如图2所示。

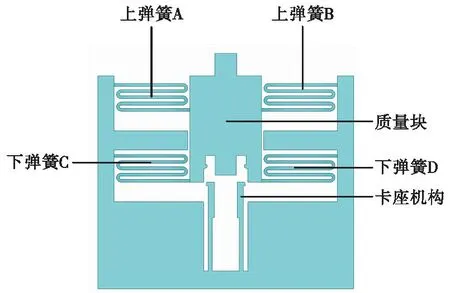
图2 后坐保险装置Fig.2 Setback arming device

在发射过程中,后坐保险装置中的可动部件质量块受到后坐力、弹簧抗力、接触反力和摩擦力的综合作用,当质量块运动到闭锁机构时受到卡座的约束,可将卡座视作悬臂梁机构,质量块基本运动可以简化为弹簧质量块阻尼系统,如图3所示。

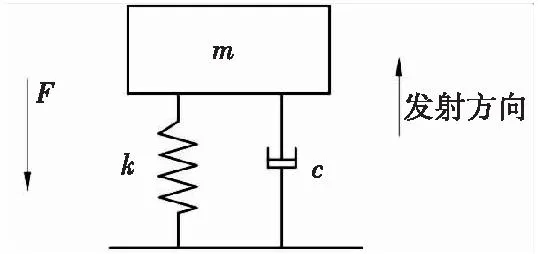
图3 弹簧质量块阻尼系统Fig.3 Spring-mass block damping system

该阻尼系统的运动微分方程为

(1)

而质量块移动时,A,B,C,D四个弹簧均受力拉伸,因此

k=k1+k2+k3+k4,

(2)

式(1)、式(2)中,m为质量块的质量,x为质量块的响应位移,c为阻尼系数,k为弹簧总刚度,F(t)为质量块受到外力的合力,k1,k2,k3,k4分别为A,B,C,D四个弹簧的刚度。

后坐保险装置受到的作用力可以用半正弦波来表示,系统阻尼为0时,在质量块运动到闭锁机构前,质量块卡头不受卡座作用,因此此时质量块受到外力的合力为F(t)=ma(t),a(t)为平行于弹轴方向的后坐加速度。

质量块运动方程可写为

(3)

(4)

质量块的最大响应位移为

(5)

后坐保险装置能够完全解除隔离的条件是卡头完全进入卡座。卡头进入卡座并被闭锁过程中,首先与卡座梁末端的卡钩碰撞,而卡头沿原方向继续运动,卡座梁受到卡头挤压作用发生偏转,直至卡头完全进入后卡座梁复位。为了便于分析,可假定卡头在冲击卡座时弹簧的拉力和卡座梁的弹力不变,弹力的大小取卡头刚好进入卡座时的临界状态,此时的受力状态如图4所示。

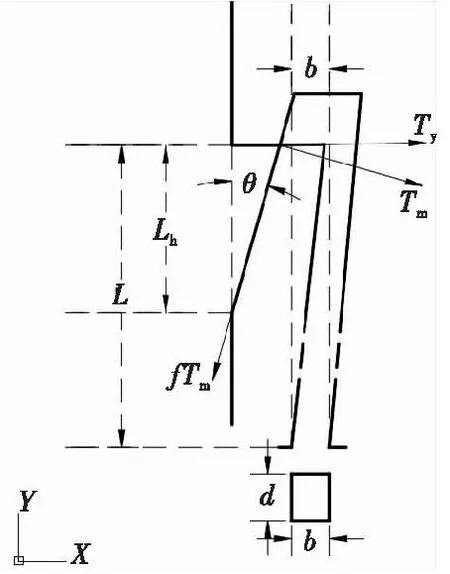
图4 质量块卡头与卡座卡头临界作用力示意图Fig.4 Schematic diagram of critical force between mass block clamp and holder clamp

质量块卡头进入卡座的阈值能量表达式为

(6)

式(6)中,E为质量块的阈值能量,E1为质量块的冲击能量,xa为质量块从静止状态到闭锁临界状态的轴向位移,Tm为临界状态下闭锁机构卡头的弹性抗力,Lh为质量块卡头顶端至卡头末端的距离,θ为卡头斜边与弹轴方向的夹角,f为动摩擦系数,d为卡座梁截面的高度,b为卡座梁等截面梁的宽度,Ty为卡座梁卡头受到的合力,L为卡座卡头底端到卡座梁末端的距离。

根据冲击能量公式E=mv2/2,质量块的冲击能量为

(7)

当质量块在进入卡座临界时刻,此时作用力最大。此时卡座梁卡头对质量块卡头的作用反力为[20]

(8)

因此,质量块卡头进入卡座的阈值能量表达式也可写为

(9)

当阈值能量E>0时,此时质量块卡头可完全进入卡座。

式(5)和式(9)为位移-能量数学模型,式(5)可用来判断后坐保险装置质量块的运动位移能否达到解除隔离位移,在可以达到解除隔离位移的前提下,式(9)可以用来判断质量块能否达到解除隔离状态,此数学模型可用来指导弹簧质量块型后坐保险装置的设计。

由无阻尼系统固有角频率计算公式可知,wn与k值有关,此外由式(9)可知,阈值能量也与k值有关,增加k值,从而减小无阻尼系统固有角频率和质量块卡头进入卡座的阈值能量,即闭锁时的冲击能量,进而提升后坐保险装置的抗过载能力。

设定典型载荷:勤务跌落载荷幅值为12 000g,脉冲宽度为200 μs;正常发射解除隔离阈值载荷幅值为20 000g,脉冲宽度为2 ms。勤务跌落载荷和正常发射载荷可简化为半正弦波形式,如图5所示。

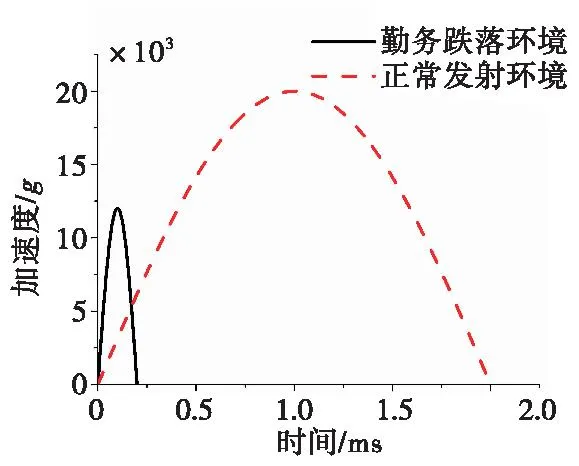
图5 后坐加速度曲线Fig.5 Setback acceleration curve

3 仿真分析

理论模型可以基本分析后坐保险装置的运动位移和闭锁条件,但较难分析后坐保险装置应力情况,为了更清楚了解后坐保险装置的解除隔离运动过程和应力情况,从而研究后坐保险装置的动态响应特性,本文利用ABAQUS有限元分析软件建立后坐保险装置有限元模型进行显示动力学分析。

由于硅材料弹性模量较低,因此弹簧形变量不能太大,结合以往设计经验,后坐保险装置的模型如图6所示。

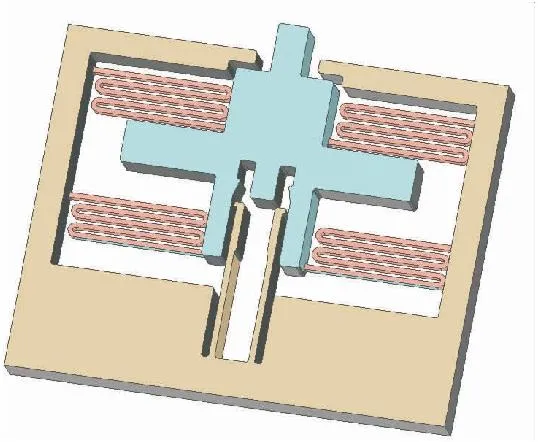
图6 后坐保险装置模型Fig.6 Setback arming device model

3.1 仿真模型

该后坐保险装置是基于单晶硅材料的MEMS机构,采用MAT-PLASTIC-KINEMATIC本构模型描述其物理行为,单晶硅材料参数如表1所示。

表1 单晶硅材料参数Tab.1 Monocrystalline silicon material parameters

由于弹簧和闭锁机构的悬臂梁部分尺寸较小,因此此处的网格为0.02 mm,其余网格为0.05 mm,如图7所示。基座为不可动件,弹簧和质量块均为可动件,且仅限制其垂直表面方向的移动自由度,摩擦系数取0.16,载荷形式为跌落和发射环境的后坐加速度,作用于质量块。

图7 网格划分Fig.7 Mesh generation

3.2 勤务和发射环境响应特性分析

本文重点对勤务跌落过载和正常发射过载下的后坐保险装置进行分析。在跌落过载和发射过载环境下后坐保险装置的应力云图和质量块的解除隔离位移如图8-图11所示。

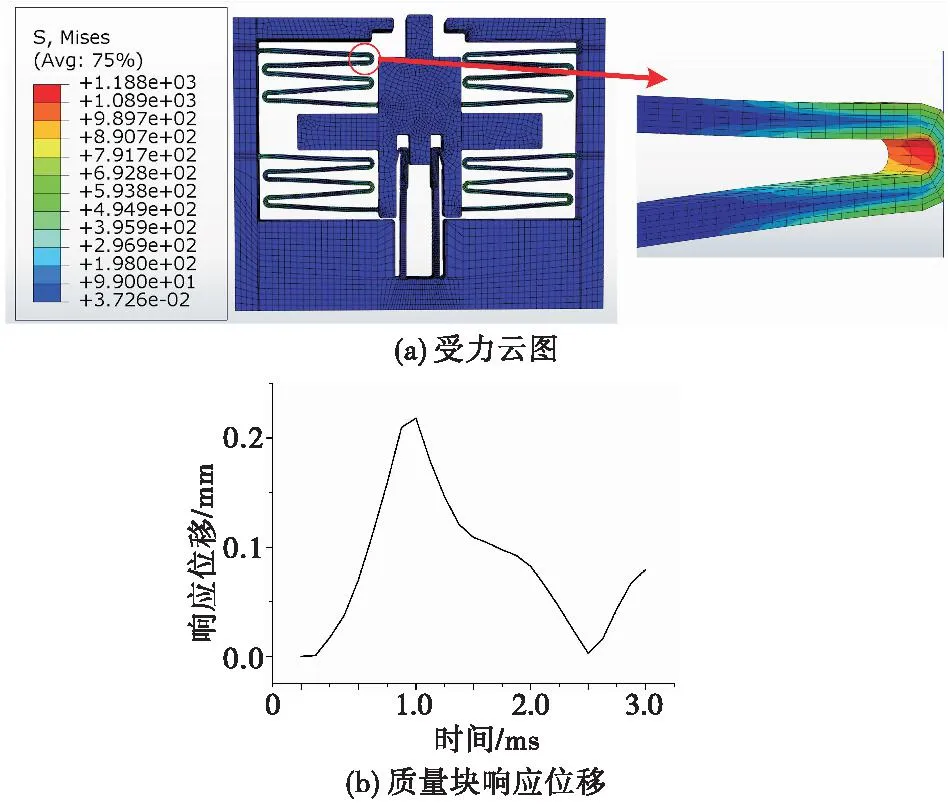
图8 勤务跌落过载仿真Fig.8 Drop overload simulation

由仿真结果图8(b)和图9(b)可知,该后坐保险装置可以区分两种环境,而从图9(b)可知,在外过载作用下,质量块运动到闭锁位置,但撤去外力后质量块离开闭锁位置,出现了闭锁脱钩的现象。

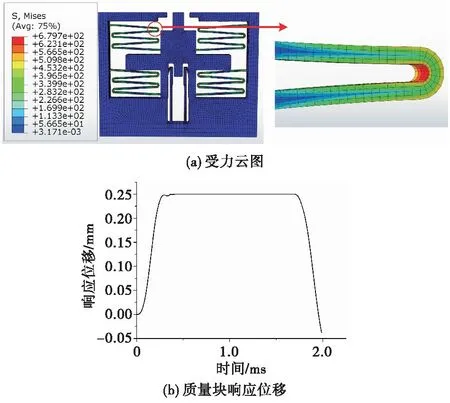
图9 正常发射过载仿真Fig.9 Launching load simulation

从图8(a)和图9(a)可知,在勤务跌落过载和正常发射过载下,弹簧受到的应力远大于其他部件,且最大应力点在靠近质量块的弹簧第一拐弯处(见图8(a)和图9(a)圆圈,以下称弹簧拐弯处),此外弹簧与基板的连接处(以下称弹簧根部)也有一定的应力集中情况,因此对这两个地方进行取点应力分析。

从图10可得,跌落环境下弹簧的最大应力值为1 188 MPa,弹簧根部的应力值也超过了硅材料的屈服极限;而从图11可得,发射环境下弹簧的最大应力值为679.7 MPa,并未超出弹簧的屈服极限。

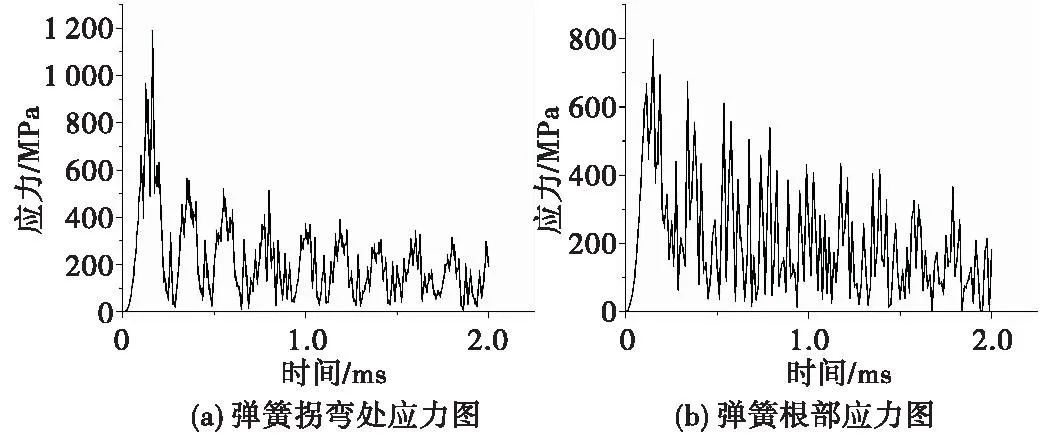
图10 勤务跌落环境下应力图Fig.10 Stress diagram in the drop environment

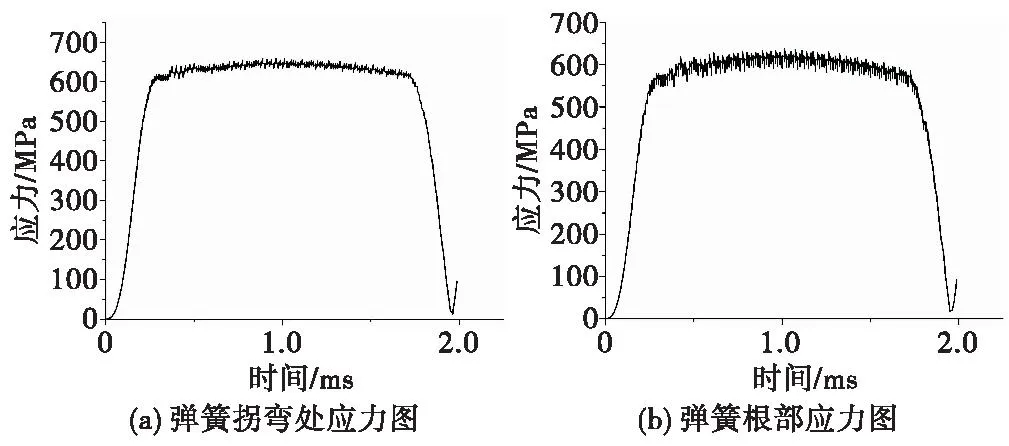
图11 正常发射环境下应力图Fig.11 Stress diagram in the launch environment

通过图10(a)和图10(b)以及图11(a)和图11(b)之间的对比可得,弹簧根部的应力峰值小于弹簧拐弯处,但随后的应力震荡程度明显强于弹簧拐弯处。从图10(a)和图11(a)对比可知,跌落环境下最大应力值高于发射环境,弹簧拐弯处更容易出现跌落环境下断裂失效问题。

3.3 弹簧厚度对应力集中的影响

由3.2节仿真结果可知,弹簧有应力集中现象,最大应力值位于弹簧拐弯处,因此接下来仿真将研究不同弹簧厚度对后坐保险装置最大应力值的影响。

初始结构弹簧厚度为0.08 mm,而基板厚度为0.3 mm,因此弹簧厚度不能超过0.3 mm,图12为不同弹簧厚度对应的勤务跌落过载和正常发射过载下后坐保险装置最大应力值图。

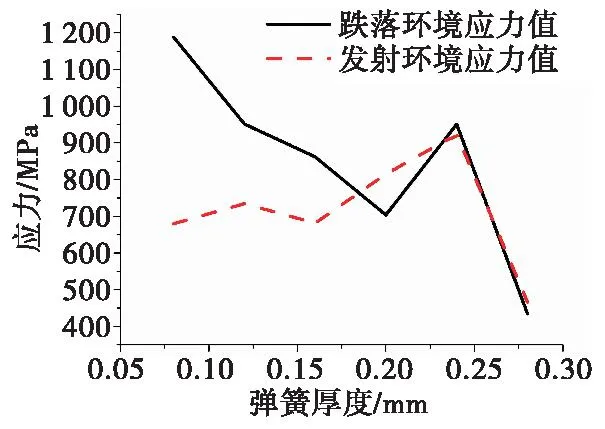
图12 弹簧厚度对最大应力值的影响Fig.12 Effect of spring thickness on maximum stress value

从图12可知:当弹簧厚度由0.08 mm增加到0.20 mm时,跌落环境下弹簧最大应力值由1 188 MPa降为703.8 MPa,最大应力值降低了40.76%,应力集中现象得到有效缓解;当弹簧厚度达到0.24 mm时,跌落环境下弹簧最大应力值急剧增加;当弹簧厚度达到0.28 mm后,在发射环境下后坐保险装置无法正常解除隔离;且最大应力值点一直位于弹簧拐弯处,此处应力集中现象严重,为后坐保险装置薄弱点。

3.4 样件测试

样机采用单晶硅体硅刻蚀工艺加工,样机成品如图13所示。

图13 样机图片Fig.13 Prototype photo

对样机进行高后坐过载失效测试,对同一批次的三组样机进行试验,载荷幅值20 000g,载荷脉宽50 μs,试验结果如图14所示。

图14 高后坐过载试验结果Fig.14 Stress diagram in the launch environment

由图14可知,两个下弹簧已完全断裂,说明弹簧根部受力严重,有应力集中现象。从放大图可知,右上方弹簧从拐弯处断裂而非根部断裂,说明弹簧拐弯处受力比弹簧根部更严重,为应力最大集中点。同时对装置进行仿真,结果表明,后坐保险装置最大应力值为1 322 MPa,最大应力点位于弹簧拐弯处,弹簧根部应力值也超出了800 MPa,均超出了硅材料的屈服强度,仿真结果与试验结果相符。

4 结论

本文对一种垂直基板式硅基MEMS后坐保险装置进行理论、仿真分析和试验测试。根据工作原理,建立了MEMS后坐保险装置的位移-能量理论模型,获取了后坐保险装置的频域运动位移响应特性和闭锁能量阈值特征。通过仿真分析和试验结果发现,靠近质量块的弹簧拐弯处为硅基后坐保险装置的最大应力集中点;闭锁机构直角卡钩易发生闭锁后弹性脱钩。当弹簧厚度不超过0.2 mm时,增加弹簧厚度,可以有效降低跌落环境下弹簧的应力集中现象,为设计提供了理论依据。未来将针对进一步降低弹簧应力集中现象开展研究,对闭锁机构直角卡钩进行结构改良,增加缓冲结构,减少闭锁时冲击碰撞的次数,提高闭锁的可靠性,改善硅基后坐保险装置的综合性能。