弹体斜侵彻弹道偏转曲线及轴向过载计算方法

王 森,崔少康,徐蓬朝,2,李睿成

(1.西安机电信息技术研究所,陕西 西安 710065;2.机电动态控制重点实验室,陕西 西安 710065)

0 引言

随着防御系统的发展,地面建筑、地下防御设施等目标建造形式普遍采用多层间隔有限厚混凝土结构。钻地武器战斗部是打击这类多层间隔混凝土目标的主要武器之一。该类武器利用其自身携带的动能以及炸药装药,使弹体侵彻目标后延时起爆,实现对地面以及地下防御设施内部装备的高效毁伤[1]。受弹靶关系及侵彻作用过程中诸多因素的影响,弹体侵彻介质时通常不是垂直入射,而是带攻角和入射角的非正规斜侵彻状态[2-3]。弹体以一定角度斜侵彻靶标时,由于弹体受到靶标的反向作用力与弹体轴向方向不一致,导致弹体在侵彻靶标的过程中弹道方向发生偏转[4-5],尤其在弹体斜侵彻多层靶标或者深层目标时,弹道方向偏转较大。

目前研究弹体斜侵彻特性比较成熟的方法为数值计算,然而在使用Ls-Dyna等有限元仿真软件进行弹体斜侵彻仿真时,求解完成后一般只能输出沿坐标轴方向的过载数据,而弹体在试验测试时一般采集的是弹体轴向或者径向的过载。当弹体在侵彻过程中,弹道偏转角度较小时,弹体轴向或者径向的过载可以用弹体沿坐标轴方向的过载数据进行近似代替;但是当弹体在侵彻过程中,弹道偏转角度较大时,两者差别较大,无法用弹体沿坐标轴方向的过载数据来代替弹体轴向或者径向的过载数据。由于弹体在斜侵彻过程中,弹道偏转角是时时变化的,因此为了获得弹体轴向或者径向的过载,就必须准确地知道弹体在任意时刻的弹道偏转角。

文献[6]建立了弹体非正侵彻混凝土薄靶有限元模型,通过仿真获得弹体斜侵彻4层混凝土靶后的弹道偏转曲线,获得弹体偏转曲线的方法是将弹体穿完每一层靶后的质心位置连成一条曲线,通过测量曲线与水平线的夹角来获得弹体的偏转曲线,这样获得的弹体偏转角与实际偏转角存在一定的误差。文献[7]利用有限元仿真软件Ls-Dyna,对弹体在不同着角和速度的初始条件下斜侵彻3层混凝土靶板的过程进行数值计算,通过仿真获得了弹体偏转角与着角和速度的关系,但是文中弹体偏转角是通过测量弹体穿透每一层靶板后那一时刻弹体的姿态与水平线的夹角获得的,不能反映弹体在穿靶过程中每一时刻的弹道偏转角。文献[8]在空腔膨胀理论基础上,基于三向加速度信息,推导出刚性弹丸零攻角斜侵彻的侵彻轨迹实时计算公式,但是是以弹丸质心的轨迹曲线代表弹丸的运动轨迹的,由于弹丸具有一定的长度,所以在斜侵彻过程中不能用弹丸质心的轨迹曲线来代表弹丸实际的运动轨迹。

针对以上问题,本文提出弹体斜侵彻弹道偏转曲线及轴向过载计算方法,用于计算弹体斜侵彻过程中弹道偏转曲线及弹体沿轴向和径向的过载曲线。

1 理论基础

1.1 弹体斜侵彻过程的运动微分方程[9]

弹体在斜侵彻过程中,由于攻角和倾角的存在会导致侵彻过程中弹体的受力不均匀,导致问题的复杂化,为使问题不失一般性,作如下假设:

1) 弹体为刚性体;

2) 弹体在侵彻过程中入射角与攻角始终处于同一平面内;

3) 弹体在侵入靶板的过程中只受质心阻力的作用,可以分解为速度方向上Ft和垂直于速度方向上的Fd,另外有一个垂直于入射平面的力矩Md,如图1 所示;

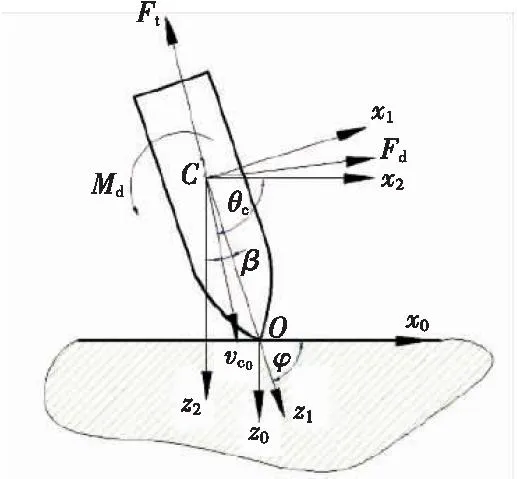
图1 弹靶坐标示意图Fig.1 Schematic diagram of missile target coordinates

4) 忽略弹体侵彻过程中的旋转带。

为方便研究问题,在弹靶作用平面建立如图1 所示的坐标系,即两组动坐标系x1Cz1和x2Cz2,与一组定坐标系x0Oz0,其中C为弹体质心,m为弹体质量,IO为绕质心轴的转动惯量,θc为弹体速度方向与水平方向的夹角,β为弹体速度方向与弹体轴线之间的夹角,φ为弹体轴线方向与水平方向的夹角。

那么弹体质心在x2Cz2坐标系下的运动方程为

(1)

(2)

IOα=-Md,

(3)

其中,α是弹体对质心的角加速度,且

(4)

由式(3)中可以看出,翻转力矩Md直接影响弹体在侵彻过程中的偏转情况。若弹体为刚体,则IO为定值,将式(4)代入式(3)得

(5)

对式(5)左右同时二次积分得

(6)

弹体为刚体,则IO为定值。由式(6)可以看出翻转力矩Md的二次积分直接影响弹体在侵彻过程中的偏转角度。

1.2 质点的运动轨迹

假设一质点以一定速度在XY平面内运动,运动轨迹如图2所示。在t=0时刻,质点沿X轴方向的位移为X0=0,沿Y轴方向的位移为Y0=0;在t=1时刻,质点沿X轴方向的位移为X1,沿Y轴方向的位移为Y1,在t=i时刻,质点沿X轴方向的位移为Xi,沿Y轴方向的位移为Yi。则在t=1时刻,质点的运动方向与X轴的夹角θ1满足方程tanθ1=Y1/X1;在任意t=i时刻,质点的运动方向与X轴的夹角θi满足方程tanθi=Yi/Xi。

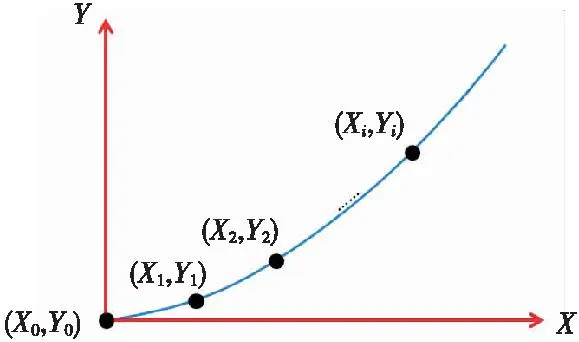
图2 质点的运动轨迹Fig.2 The motion trajectory of particles

2 弹体斜侵彻弹道偏转曲线及轴向过载计算方法

本文提出的弹体斜侵彻弹道偏转曲线及轴向过载计算方法是在动力学仿真的基础上实现的,首先需要完成弹体斜侵彻靶标的动力学仿真计算,获得弹体沿坐标轴方向的过载曲线及弹体上沿弹体轴向任意两点的位移曲线,然后计算出弹体斜侵彻过程中的弹道偏转曲线及弹体沿轴向和径向的过载曲线,计算流程如图3所示。

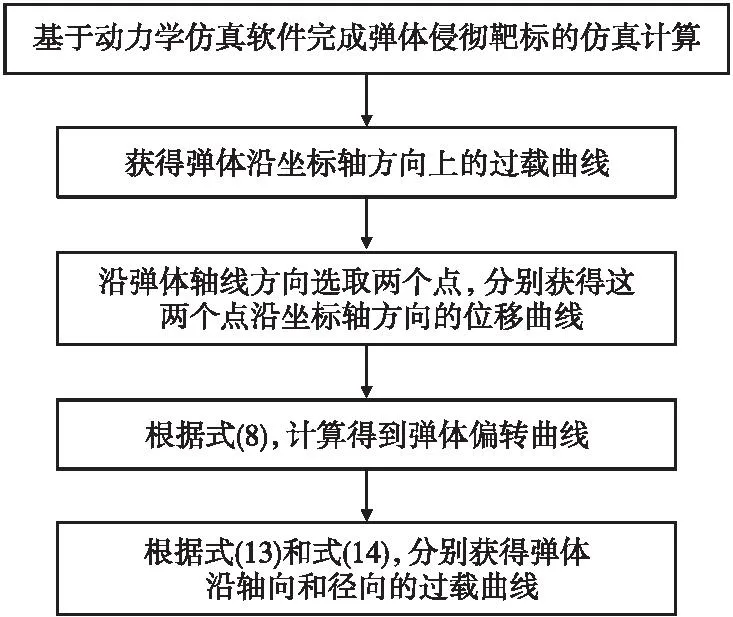
图3 弹道偏转曲线及过载计算流程Fig.3 Ballistic deflection curve and overload calculation process

在进行弹体侵彻靶标仿真分析时,为了方便获得弹体过载数据和弹体弹道偏转曲线,建模时初始时刻弹体轴线方向与坐标轴X轴方向重合,如图4所示。斜侵彻计算时,假定弹体长度为L,弹体轴线方向与X轴方向夹角为θ,t为时间,t0为初始时刻,ti为任意时刻,弹体在侵靶过程中不同时刻的姿态如图5所示。沿弹体轴向选取两个点,分别为A点和B点,为方便计算,本文选取弹底正中心位置为A点,选取弹尖位置为B点,这样A点与B点沿弹体轴向的距离就等于弹长L,AXi为ti时刻A点沿X轴方向的位移,AYi为ti时刻A点沿Y轴方向的位移,BXi为ti时刻B点沿X轴方向的位移,BYi为ti时刻B点沿Y轴方向的位移。

图4 初始时刻弹体位置与坐标轴关系Fig.4 The relationship between the initial position of the projectile and the coordinate axis

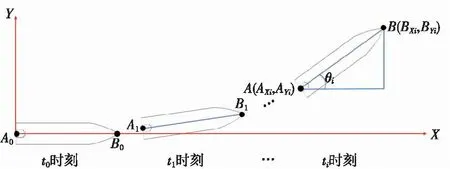
图5 任意时刻弹体姿态Fig.5 Body attitude at any time

如图5所示,初始时刻,弹体的弹轴方向与X轴方向一致,在ti时刻,弹体的弹轴方向与X轴方向夹角为θi,则

(7)

(8)

假定通过动力学仿真软件获得的弹体沿X轴方向的过载为axi,沿Y轴方向的过载为ayi,按照图6所示将弹体沿X轴方向的过载axi和沿Y轴方向的过载ayi分解到沿弹轴方向和垂直于弹轴方向(径向)上的两个分量,则

图6 弹体沿坐标轴方向过载的分解图Fig.6 Decomposition diagram of projectile overload along the coordinate axis direction

axi在弹体轴向的分量为

axi轴=axi·cosθi。

(9)

axi在弹体径向的分量为

axi径=-ayi·sinθi。

(10)

ayi在弹体轴向的分量为

ayi轴=ayi·sinθi。

(11)

ayi在弹体径向的分量为

ayi径=ayi·cosθi。

(12)

因此,弹体沿轴向的过载ai轴等于axi在弹体轴向的分量与ayi在弹体轴向的分量之和,即

ai轴=axi·cosθi+ayi·sinθi。

(13)

弹体沿径向的过载ai径等于axi在弹体径向的分量与ayi在弹体径向的分量之和,由于两个分量方向相反,即

ai径=ayi·cosθi-axi·sinθi。

(14)

3 算例验证

3.1 基于Ls-Dyna的弹体侵靶仿真计算

本文以弹体斜侵彻深层土壤为例,进行弹体侵靶动力学仿真计算,仿真时使用的软件为有限元仿真软件Ls-Dyna,弹体长度为1.25 m,直径0.3 m,初速为800 m/s,着角为20°,土壤厚度为6 m,仿真模型如图7(a)所示,图7(b)-图7(i)为弹体侵彻过程中典型时刻的穿靶姿态图。

图7 弹体仿真模型及不同时刻弹体姿态Fig.7 Simulation model of projectile and posture diagram of projectile at different times

通过测量弹体轴线与X轴夹角的方式得到弹体不同时刻的弹道偏转角,具体方法:首先将弹尖和弹体尾部中心点连成一条直线,用该直线方向代表弹体的轴向;其次过弹体尾部中心点作一条水平线;最后用高精度角度尺测量这两条线之间夹角,该夹角即为弹体的偏转角度,测量示意图如图8所示,具体测量结果如表1所示。

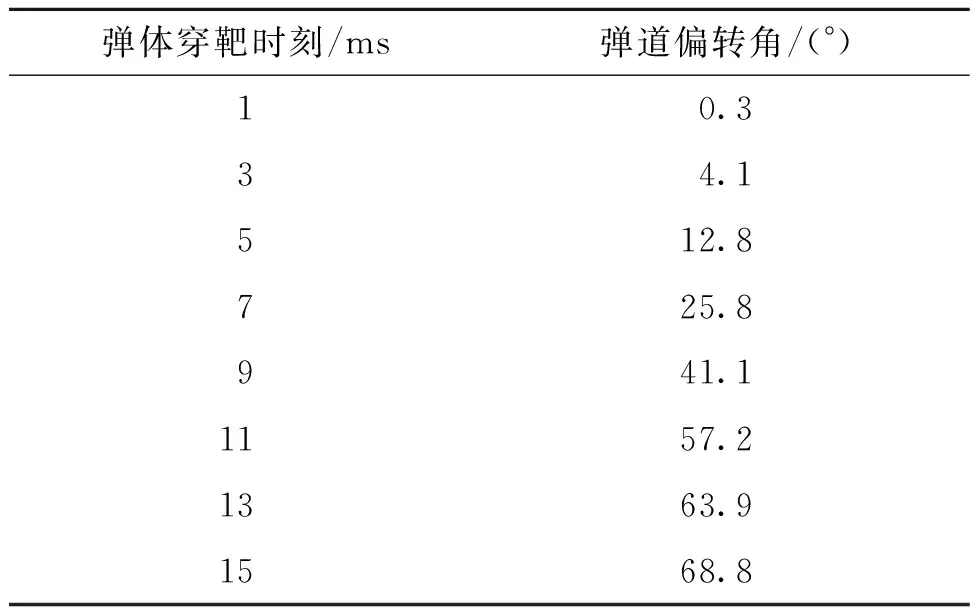
表1 不同时刻弹体弹道偏转角Tab.1 Comparison table of test and simulation results

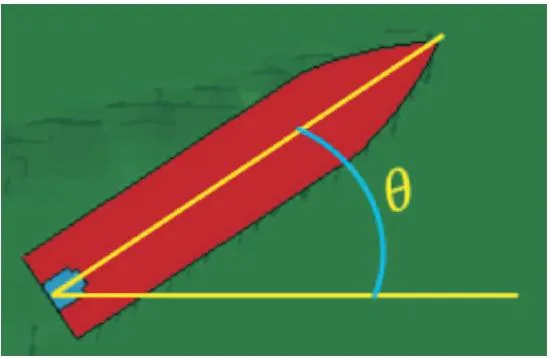
图8 弹体弹道偏转角测量示意图Fig.8 Measurement diagram of projectile deflection angle

通过仿真,获得弹体沿X,Y轴方向的过载如图9所示,弹体上A点沿X,Y轴方向的位移曲线如图10所示,弹体上B点沿X,Y轴方向的位移曲线如图11所示。

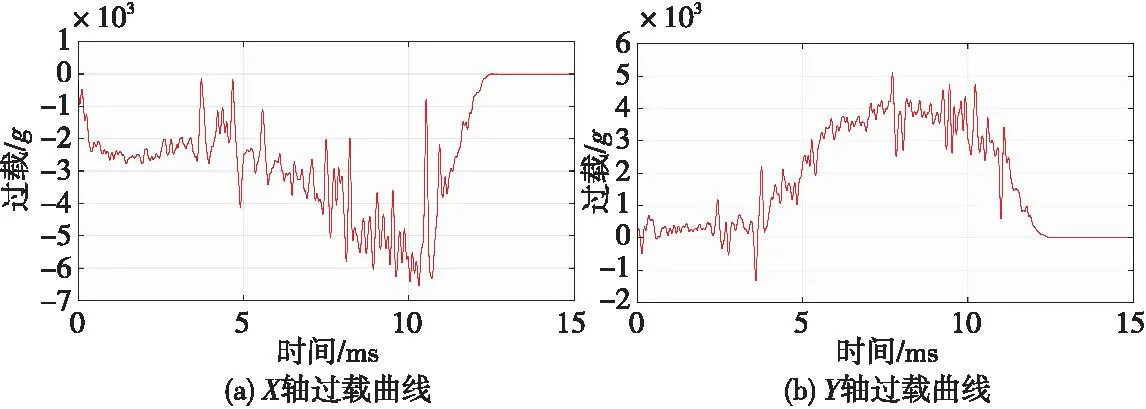
图9 弹体沿X轴、Y轴过载曲线Fig.9 Overload curve of the projectile along the X-axis and Y-axis

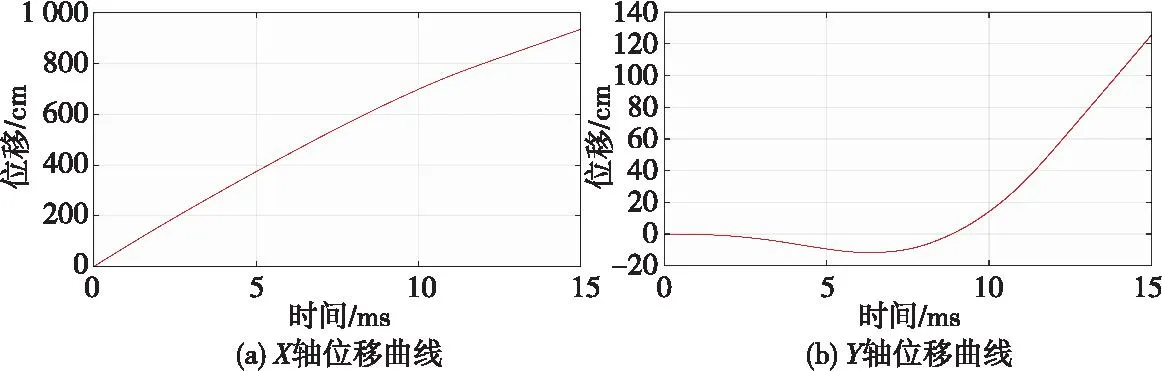
图10 A点沿X轴、Y轴位移曲线Fig.10 Displacement curves of point A along the X-axis and Y-axis

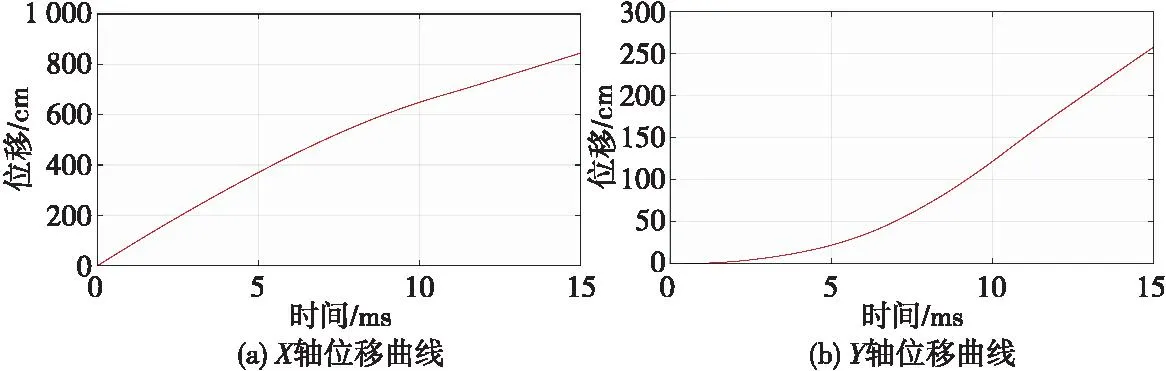
图11 B点沿X轴、Y轴位移曲线Fig.11 Displacement curves of point B along the X-axis and Y-axis

3.2 弹道偏转角和轴向过载计算

1) 弹体弹道偏转角的计算

将弹体A点和B点的位移曲线,代入式(8),经过计算,得到弹体的弹道偏转曲线如图12所示。

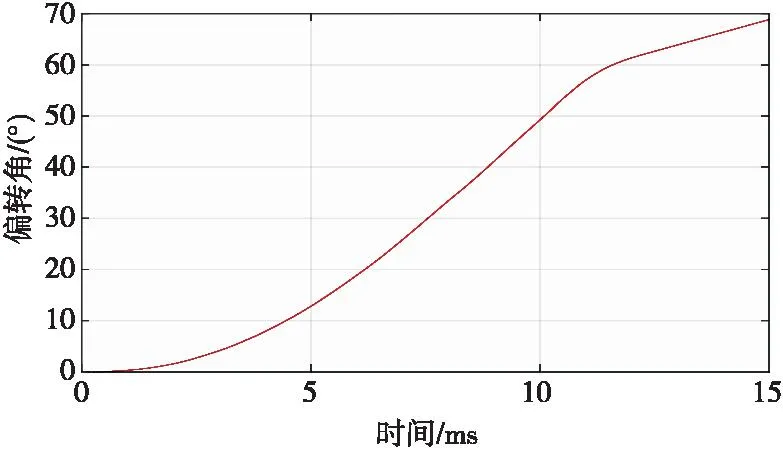
图12 本文方法计算出的弹道偏转曲线Fig.12 The ballistic deflection curve calculated by the method in this article

由图12可知,弹体在侵彻土壤的过程中,弹体的弹道发生了较大的偏转,将图12的结果与表1中的数据进行对比,结果如表2所示。由表2可知,通过本文方法计算出的弹体弹道偏转角与测量出来的偏转角误差较小,最大误差不超过4%,说明本文的计算方法可以较准确地计算出弹体斜侵彻过程中的弹道偏转角。

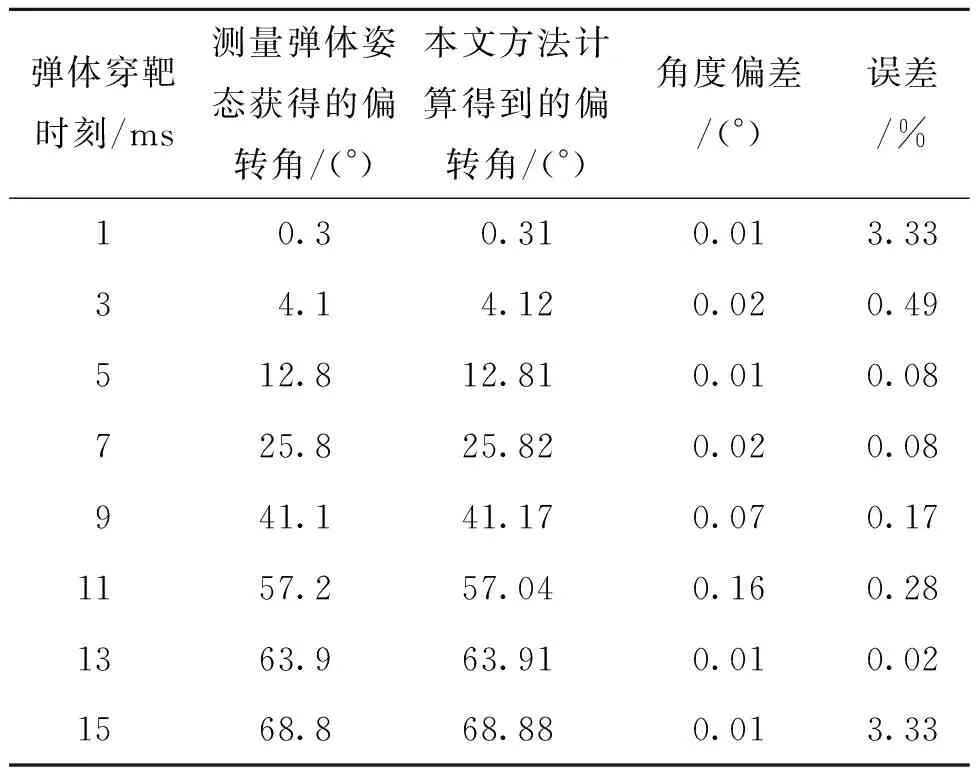
表2 弹道偏转角对比表Tab.2 Comparison table of ballistic deflection angle

2) 弹体沿轴向和径向的过载曲线

将图12的弹道偏转角代入式(13)和式(14),分别获得了弹体在侵靶过程中的轴向过载和径向过载,如图13所示。将弹体轴向过载与X轴方向过载对比分析,结果如图14(a)所示。由图中可以看出初始时刻,轴向过载与X轴方向过载大小一致;大概在弹体侵靶5 ms以后,随着弹道偏转角的增大,轴向过载与X轴方向过载发生明显差异,弹体轴向过载明显小于弹体沿X轴方向的过载。将弹体径向过载与Y轴方向过载对比分析,结果如图14(b)所示。由图中可以看出:初始时刻,径向过载与Y轴方向过载大小一致;大概在弹体侵靶5 ms以后,随着弹道偏转角的增大,径向过载与Y轴方向过载发生明显差异,弹体径向过载明显大于弹体沿Y轴方向的过载。

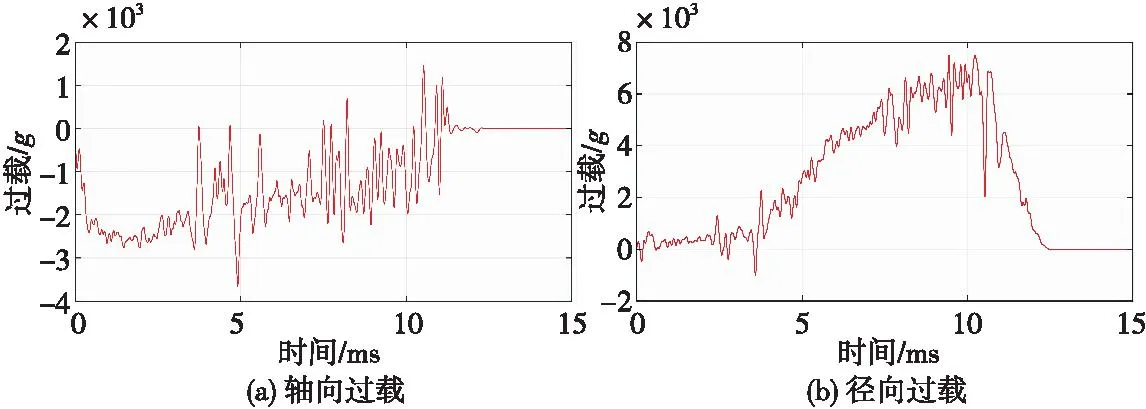
图13 弹体轴向、径向过载曲线Fig.13 Axial and radial overload curves of the projectile

4 结论

本文提出弹体斜侵彻弹道偏转曲线及轴向过载计算方法,通过该方法较准确地计算出弹体在斜侵彻靶标过程中的弹道偏转曲线,并且根据弹道偏转曲线获得弹体轴向和径向的过载曲线,将获得的弹体轴向和径向的过载与弹体沿坐标轴方向的过载进行对比,发现在弹体偏转角度较大的情况下,两条曲线的峰值和走势差别较大,因此当弹体在斜侵彻过程中弹道偏转角度较大的情况下,不能用弹体沿坐标轴方向的过载曲线代来代替弹体轴向和径向的过载曲线。