外圆磨削非线性动力学模型与实验验证*
封 超 张金峰 许芝令 王保义
(①山东科技大学工程实训中心,山东 青岛 266590;②山东科技大学机电工程学院,山东 青岛 266590;③青岛海空压力容器有限公司,山东 青岛 266000;④济南重工集团有限公司,山东 济南 250100)
颤振思想源于对切削加工的研究,切削颤振是在20 世纪初由Taylor F[1]提出的。Arnold R N[2]对车削过程中颤振的产生机理进行了较为详细的描述,并构建了颤振理论的动力学基础。系统开始失稳后,颤振就随之发生,表现形式不尽相同,最终表现在零件成型后的表面质量上。Arnold 指出,每轮完成的加工表面转成下一轮切屑的上表面。由于切屑的厚度会影响切削力,因此表面再生的现象造成切削力不仅与当前工件和刀具间的相对位置有关,还与上个切削周期的相对位置有关。根据Arnold 的理论,Tobias S A[3]、Tlustry J[4]、Altintas Y[5]分别建立了关于车削再生颤振的结构稳定性和动力学模型。
在微磨削过程中,微磨削系统的不稳定是直接影响微磨削的加工质量和精度的原因之一,研究磨削颤振对提高磨削加工的稳定性以及提升工件质量有重要的意义。最初是以Snoeys R[6]模型为基础对系统稳定性展开研究并揭示颤振的过程。Inasaki I[7]等利用磨削过程的特征方程研究方程解从而得出磨削加工的稳定极限和不稳定增长指数。Hashimoto F[8]对砂轮和工件间的动态干涉的表述、颤振的增长速率以及接触刚度的处理都进行了理论研究和实验分析。Srinvasan K[9]系统研究了特征方程及其根的分布规律。Weck M[10]和Chung K[11]分别对工件和砂轮的再生颤振理论展开了系统性研究。近几年,外圆磨削在模型构建[12],摩擦效应[13],检测方法与分析[14],表面质量[15]及纳米磨削[16]等方面有很大进展,但是从非线性动力学出发探究外圆磨削特性的较少,因此,本文对外圆磨削颤振展开详细建模与实验分析。
1 动力学模型的建立与求解
1.1 动力学模型建立
磨削加工中,砂轮安装在砂轮机上,工件被夹具固定。为了实现连续磨削,工作过程中砂轮以较高的转速旋转,并沿工件的轴线做直线往复运动。将磨削系统等效为弹簧质量模型,如图1 所示。
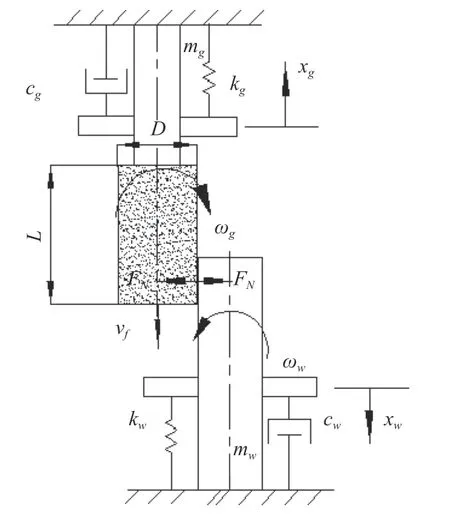
图1 磨削加工动力学模型
被加工工件w以恒定角速度ωw旋转,视为质量弹簧振子之一,其质量是mw、阻尼是cw、刚度是kw。砂轮装到机床上且平行于工件,定义为另一个质量弹簧振子,以转速ωg旋转,同时沿工件水平方向以速度vf移动,砂轮质量是mg、等效直径是D、刚度是kg、磨粒有效长度是L、阻尼是cg。根据磨削过程动力学[11],计算得出磨削系统的非线性延迟微分方程为
式中:砂轮质量m1,mg;工件质量m2,mg;砂轮阻尼c1,Ns/mm;工件阻尼c2,Ns/mm;砂轮刚度k1,N/mm;工件刚度k2,N/mm;δxs指机床施加初始进给后产生的静态切削深度,mm;δxd是工件与砂轮动态作用下的动态切削深度,mm;磨削加工某一瞬时的总切削深度δ为二者之和,在研究线性稳定边界时二者是关键因素。
式中:K是磨削力系数,N/mm;s1是微砂轮刃密度,mm-2;γ、ε是指数参数;vw是工件线速度,mm/s;vg是微砂轮的线速度,mm/s;D是等效砂轮直径,mm。
经验系数β是介于0 和1 之间的因子(0<β<1)。FNS是静态接触力,N,其表达式为
式中:Sf是机床对工件施加的初始进给量,mm。
式中:τ1表示砂轮因材料损失而产生位移所引起的时间延迟,s;τ2表示工件的时间延迟,s;τ1=2π/ω1,τ2=2π/ω2;ω1是砂轮转速,rad/s;ω2是工件转速,rad/s;α是重叠因子,定义为
式中:w2表示砂轮的横向宽度,mm;vf是砂轮的横向速度,mm/s。
1.2 动力学模型微分方程
假设(x1,x2)=(δxsp,δxdq)是式(1)的平衡点,那么p和q应该满足如下关系:
进行坐标变换把平衡点移到原点,得到式(1)的三阶展开式为
式(8)中: δy=x-xτ1-(y-αyτ2),h=K′ε(δxsr)ε-1,ε11=
由于非线性方程无法用来直接研究加工参数对磨削过程稳定性的影响,根据稳定边界理论求特征值,需要对非线性模型进行数值线性处理,然后在特征参数的基础上研究各个加工参数对磨削过程稳定性的影响。对时滞微分方程进行线性化处理,得到系统稳定性方程为
1.3 方程特征根
用数值分析对参数(ωg,ωw,vf,δxs) 进行稳定区域的确定,具体方法为:对于给定的控制参数值,根据Thompson 颤振理论,假设λd为特征值,引入Faddeev 算法求解方程,通过特征值的实部F(ωg,ωw,vf,δxs) =Re(λd)来定义实函数F,多项式λ通过递归公式推出:
欧拉公式对F(ωg,ωw,vf,δxs) =Re(λd)进行数值处理,得出各参数微分方程特征值的具体表达式如下:
综上所述,影响非线性模型参数稳定的变量除了进给速度、等效砂轮长度、等效砂轮直径外,初始进给量以及磨粒分布密度等也起关键作用,针对不同参数展开多因素研究才能对加工稳定性影响因素有更全面的掌握。
2 实验验证
根据 Kuhn H W 的算法[17],分别对时域响应图以及特征根分布图进行Matlab 数值模拟,通过改变参数,得到不同的特征值位置图,分析特征值的变化规律对参数稳定图的影响,得出预测方法的可行性、结果的准确性。
2.1 进给速度实验
为了得到参数空间中不同速度下的(ωg,ωw,vf)空间曲线,设定初始加工参数分别是:砂轮刃密度s1=1 300 mm-2,砂轮转速ωg=3 140 rad/s,进给速度vf=10 mm/min,等效砂轮长度L=12 mm,初始进给量Sf=0.002 mm,等效砂轮直径D=0.5 mm,磨削力系数K=2 400 N/mm。为了判断磨削过程的稳定性,绘制出一组以vf为变量的参数稳定图,如图2a和图2b 所示的用函数曲面的截面研究参数空间中当曲面F为0 的轮廓。
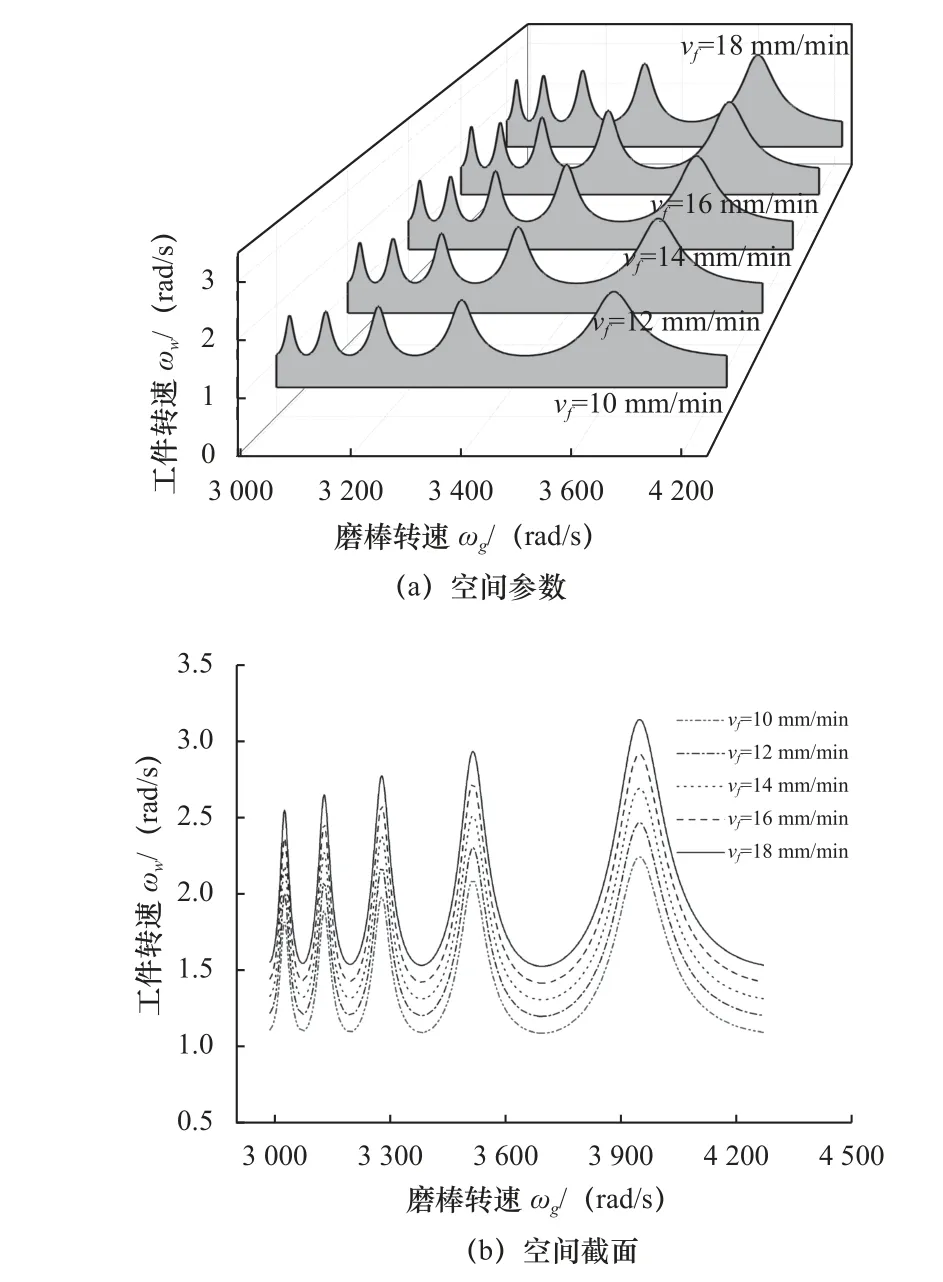
图2 不同进给速度下的参数稳定图
图2 a 中,水平线是保证磨削过程重叠的下限,曲线是代表加工是否稳定的上限,阴影区域是磨削加工过程中不发生颤振的有效空间。综合图2,vf=10 mm/min 时的阴影面积最小,vf=12 mm/min 时阴影面积增加,而vf=18 mm/min 时阴影面积最大,即稳定区域是随进给速度的增大而增加的。
下面分别从时域和特征值两方面对图2 的正确性进行验证。
设定ωw=1.2 rad/s,ωg=3 140 rad/s,L=12 mm,D=0.5 mm,s1=1 300 mm-2初始进给量sf=0.002 mm,比例系数K=2 400 N/mm,如图3 所示。选取不同的进给速度,发现进给速度为10 mm/min 时,磨削中出现颤振现象,如图3a 所示;进给速度增至12 mm/min 时磨削过程趋于稳定,如图3b 所示。
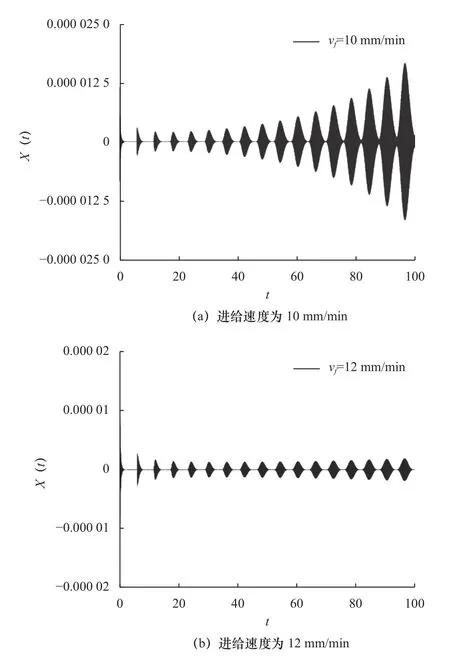
图3 不同进给速度下的时域响应图
图4 为选取与图3 相同的参数设置,进给速度从10 mm/min 提高到12 mm/min 所绘制的特征值位置图,观察发现图4a 存在部分特征值实部大于零,即磨削过程有不稳定现象,而图4b 的特征值实部均为负数,可见图4b 是稳定磨削加工。进给速度的提高使特征值向左移动引起磨削过程从不稳定到稳定状态的转变。
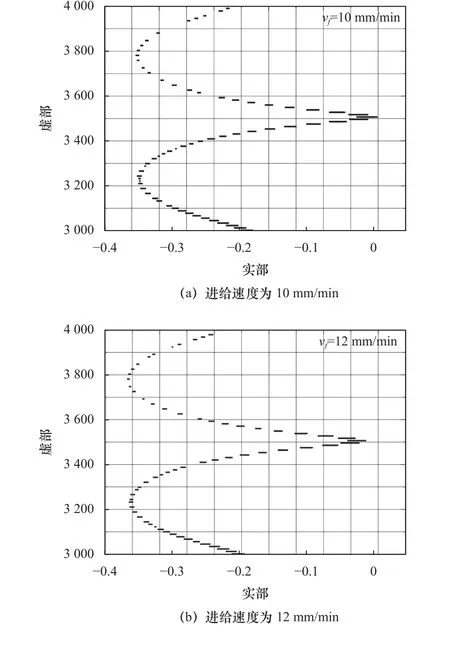
图4 不同进给速度下的特征值位置变化图
综合图2~图4 的研究结果,得出参数稳定图、时域响应图和特征值位置图三者关于进给速度对磨削加工过程稳定性的结论是一致的。
2.2 砂轮长度实验
式(6)中砂轮的长度影响重叠因子大小,最终影响预测模型的稳定性,图5 对不同砂轮长度时加工稳定性变化研究。砂轮刃密度s1=1 300 mm-2,砂轮转速ωg=3 140 rad/s,进给速度vf=10 mm/min,工件转速ωw=1.25 rad/s,初始进给量Sf=0.002 mm,等效砂轮直径D=0.5 mm,磨削力系数K=2 400 N/mm。为了判断磨削过程的稳定性,绘制出一组以砂轮长度L为变量的参数稳定图如图5a 所示,图5b 所示为用函数曲面的截面研究参数空间中当曲面F为0的轮廓绘制的截面图。
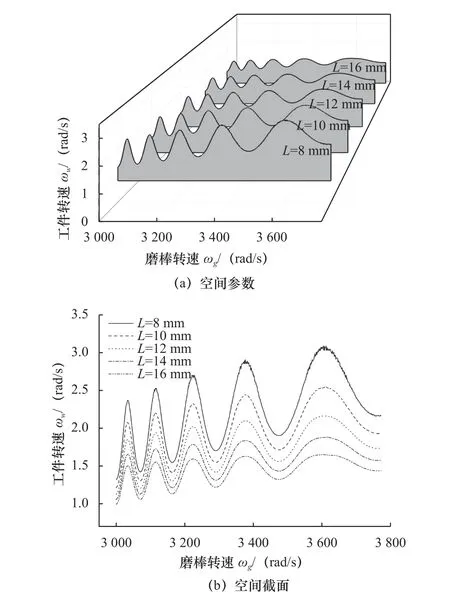
图5 不同砂轮长度时的空间参数稳定图
图5 中,砂轮长度增加,极限稳定性曲线上限在减小,表示磨削重叠下限的水平线也是减小的。综合图5,砂轮长度L为16 mm 时的阴影面积最小,L为14 mm 时阴影面积增加,实验数据中L为8 mm时阴影面积最大,即稳定区域是随砂轮长度的增大而减少的。
下面分别从时域和特征值两方面对图5 的正确性进行验证。
设定工件转速ωw=1.3 rad/s,砂轮转速ωg=3 140 rad/s,砂轮直径D=0.5 mm,进给速度vf=10 mm/min,砂轮刃密度s1=1 300 mm-2,初始进给量sf=0.002 mm,比例系数K=2 400 N/mm。如图6 所示,选取不同的砂轮长度L,发现L=12 mm 时,过程趋于稳定,如图6a 所示;但砂轮长度增至14 mm 时磨削过程出现颤振现象,如图6b 所示。
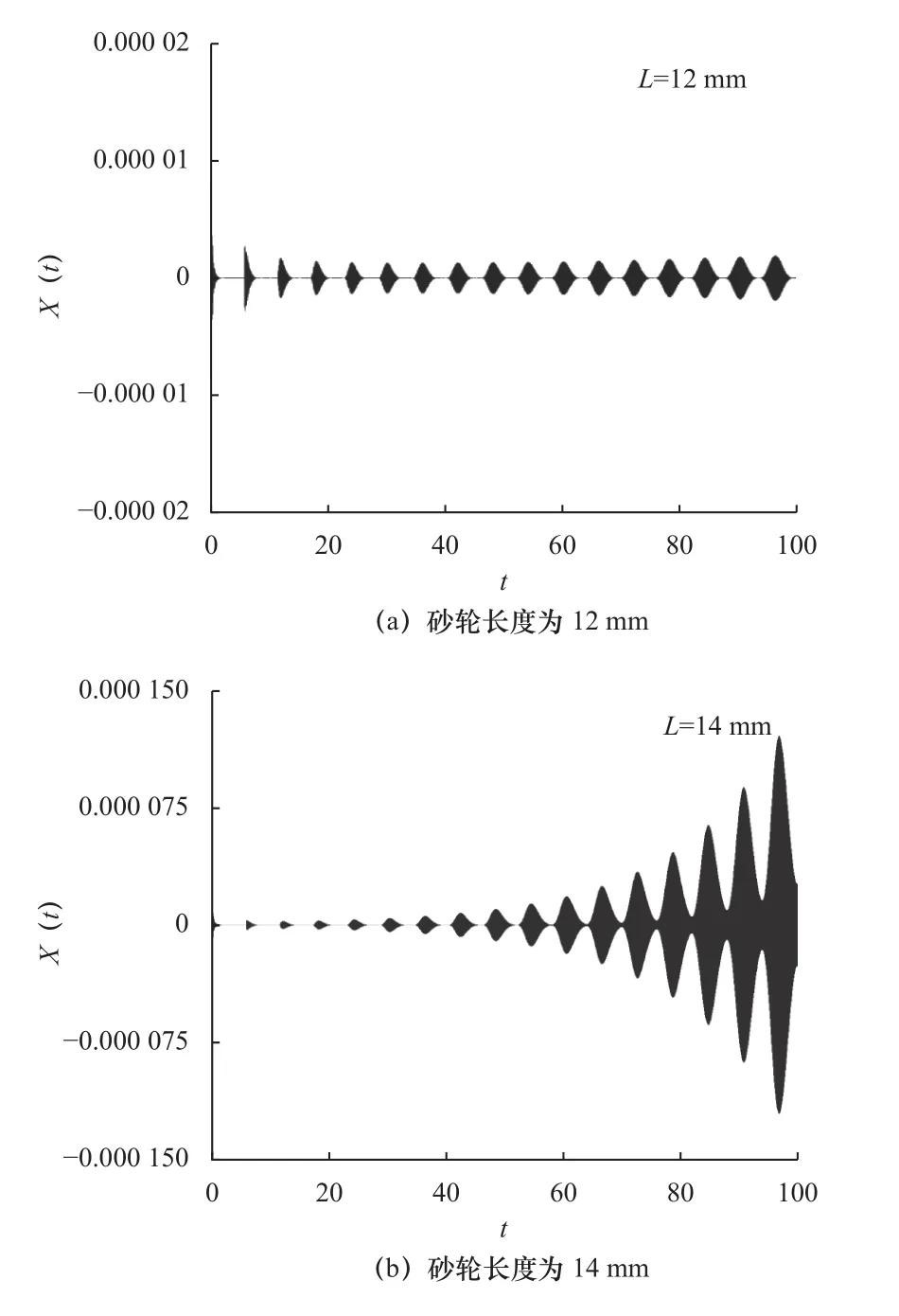
图6 不同砂轮长度的时域响应图
图7 为选取与图6 相同的参数设置,砂轮长度从12 mm 增大到14 mm 所绘制的特征值位置图,观察发现图7a 特征值实部均为负数,是稳定磨削加工;而图7b 存在部分特征值实部大于零的现象,即磨削过程不稳定。砂轮长度的增加使特征值向右移动引起磨削过程从稳定到不稳定状态的转变。
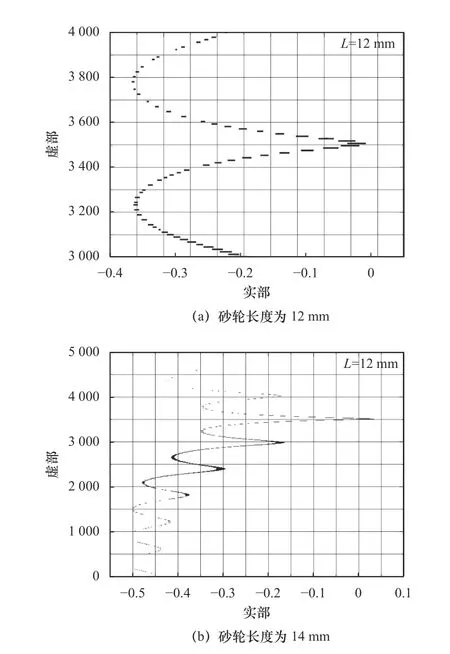
图7 不同砂轮长度的特征值位置图
综合图5~图7 的研究结果,得出参数稳定图、时域响应图和特征值位置图三者关于砂轮长度对磨削加工过程稳定性的结论是一致的。
3 结语
为了提高磨削加工的产品表面质量,从3 个方面开展研究并取得结论如下:
(1)对比磨削动力学宏观结构构建起非线性动力学微观模型,并推导出磨削非线性动力学方程。
(2)对非线性动力学方程进行线性化处理计算出系统特征值,并进行稳定性预测,得出影响系统稳定性的因素,主要包括等效砂轮长度、砂轮转速、进给速度、磨粒分布密度、等效砂轮直径、初始进量、磨削力系数和工件转速等。
(3)以进给速度和砂轮长度为例,使用Matlab绘制出各因素不同取值时一系列的稳定区域图,并研究各参数在状态变化转折点所对应的时域响应图和特征值位置图,发现进给速度从10 mm/min 提高到12 mm/min 时磨削过程从不稳定转变为稳定状态,而砂轮长度从12 mm 增大到14 mm 时磨削过程从稳定转变为不稳定状态;对稳定图、时域响应图、特征值位置图三者综合分析,发现得到的结论均一致,由此证明动力学模型的正确性。

