基于匝数气隙双分段的改进绕组函数解析分析方法*

倪荣刚 蔡亚倩 韩思雨 赵 咏

(1.青岛大学电气工程学院 青岛 266071；2.大连海事大学船舶电气工程学院 大连 116026)

1 引言

近年来，随着高端制造业的飞速发展，位置伺服系统已广泛应用于航空航天、电动汽车、机器人等领域[1]。位置检测是位置伺服系统最主要的需求之一[2-5]。目前常用的位置传感器有三种，分别为光学编码器、霍尔传感器[6]和旋转变压器[7]。光学编码器基于光电原理，具有体积小、精度高等优点。然而，光学编码器由于复杂的光学结构、较高的制造成本以及对应用环境的苛刻要求等缺点，其广泛应用受到了限制[8]。相比之下，旋转变压器性能更加优越。在所有的旋转变压器中，可变磁阻式旋转变压器(Variable reluctance resolvers，VRRs)凭借其结构简单、可靠性高以及经久耐用等优点脱颖而出[9-11]，并被广泛应用于高温、高湿、强振动等工作环境[12-14]。

解析分析法和有限元法[15-18](Finite element analysis，FEA)都可用于分析VRR 的电磁性能。前者最具代表性的方法是绕组函数法[19](Winding function approach，WFA)和改进的绕组函数法[20-22](Modified winding function approach，MWFA)。WFA 于1998年被提出[23]，主要用于分析均匀气隙电机。为了准确分析非均匀气隙，在 WFA 的基础上提出了MWFA。文献[24]提出了一种基于WFA 建立电机数学模型的方法，并利用该方法建立了可变磁通磁阻电机的数学模型。文献[25]在WFA 的基础上建立了具有对称绕组结构的双三相永磁同步电机解析模型，计算了相间自感和互感，并与FEA 分析结果进行对比，验证了计算结果的准确性。文献[26]利用MWFA 对三相凸极同步电机进行建模，并考虑了多种非理想因素。

众所周知，永磁同步电机(Permanent magnet synchronous machines，PMSMs)具有效率高、功率因数高、起动转矩大等优点[27-29]，在功率转换方面具有优势[30-32]。因此，文献[33]提出了一种将VRR作为内电机径向集成在PMSM 内部的混合双定子电机结构，而后采用MWFA 对其内电机进行解析分析。然而，槽开口处的气隙磁通密度以及励磁绕组自感波形与FEA 结果存在拓扑差异。针对上述问题，本文对线圈匝数分布函数和气隙函数进行修正，并提出分段绕组函数法(Segmented winding function method，SWFM)。

本文结构安排如下。首先，介绍电机模型及其主要参数，并给出MWFA 和漏感的计算公式。然后，阐述线圈匝数分布函数的修正过程，并计算气隙磁通密度。最后，对气隙函数进行修正后提出SWFM，并采用该方法对VRR 进行解析分析，将计算结果与FEA 分析结果进行对比，验证其有效性。

2 解析模型与传统计算方法

2.1 模型及主要参数

将VRR 集成到PMSM 中，可以减少安装位置传感器所占用的轴向空间，提高系统转矩密度。混合双定子电机的结构如图1 所示。

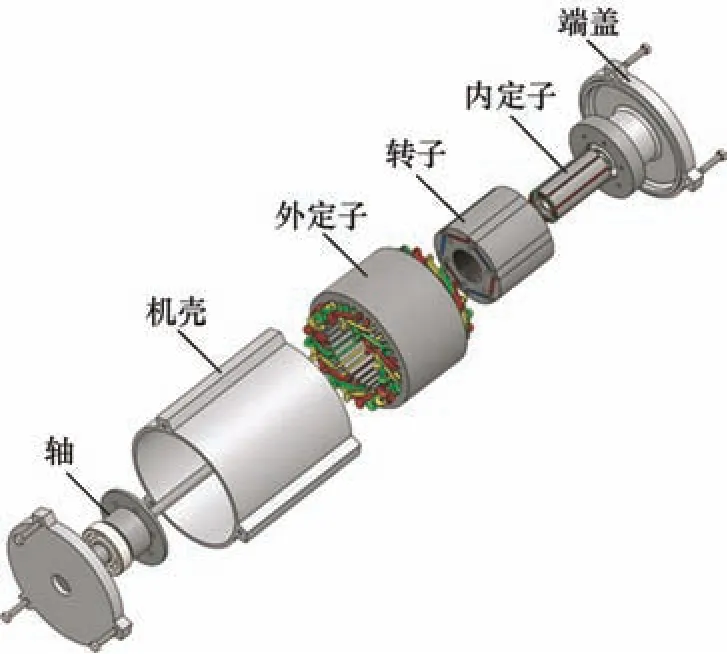
图1 混合双定子电机结构图

混合双定子电机的横截面如图2 所示。外电机为6极36槽的PMSM，内电机为8槽的内定子VRR。其中，内定子VRR 三维模型如图3 所示，其中ϕRef为静止坐标系参考点，取为励磁绕组和余弦绕组的公共轴线；θRef为旋转坐标系参考点，取为最小气隙与ϕRef重合处。S为旋变定子外缘的圆柱面。路径abcd为在静止参考系中绘制的一个扇形，其中直线和直线分别沿径向垂直穿过气隙，被气隙截取为直线和直线。

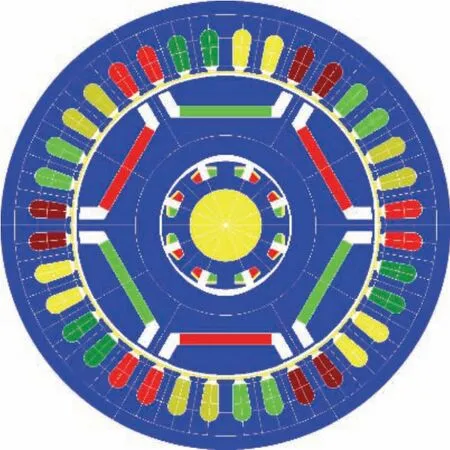
图2 混合双定子机器的横截面图

图3 VRR 三维模型及标注

图3 中，sφ和tφ分别表示一个定子槽和一个定子齿所跨过的角度，二者满足

式中，Z为定子槽数，由模型可知其值为8。

VRR 共有三套绕组，分别为励磁绕组、正弦绕组和余弦绕组，其最大每齿匝数分别用Nexc、Nsin和Ncos表示。VRR 的主要参数如表1 所示。

表1 VRR 的主要参数

该VRR 的气隙长度随机械角度的变化而变化，即气隙长度是不均匀的。气隙长度与机械角度的关系定义为气隙函数，用g(ϕ,θ)表示为

式中，θ和ϕ分别表示从θRef和ϕRef开始的角度；K代表调整因子，综合考虑各种因素，K取值为1.6。

图3 中提出的模型是基于MWFA 的。在分析之前，作出如下假设：① 磁性材料的磁导率无穷大；② 端部漏感忽略不计；③ 线圈匝数分布函数为阶跃函数；④ 气隙函数不计槽开口。

2.2 常规计算方法

由于正弦绕组和余弦绕组电流几乎为零，因此只考虑励磁电流。由安培定律可知，沿闭合路径abcd的磁场强度H满足

式中，iexc代表励磁绕组电流；nexc是励磁绕组的线圈匝数分布函数；F为磁动势。

对于图3 中的S，根据高斯定律可得

式中，B为磁通密度；H(ϕ,θ)为气隙磁场强度的径向分量；μ0为空气磁导率。Rso和Lef的取值参考表1。

经分析计算，可得改进绕组函数为

这里有

其中

因此，气隙磁通密度为

励磁绕组中的磁链为

励磁绕组的电枢自感为

同理可得，励磁绕组和正余弦绕组磁链为

励磁绕组和正余弦绕组之间的电枢互感为

2.3 漏感的计算

漏感主要由槽漏感、齿顶漏感和端部漏感组成。根据假设②可知端部漏感忽略不计。由于漏感的计算不是本文重点，因此只给出了槽漏感和齿顶漏感的基本计算公式，不再详细分析。

槽漏感为

式中，λσs为槽比漏磁导。

齿顶漏感为

式中，λσt为齿顶比漏磁导，可以表示为

式中，gavg为VRR 的平均气隙长度，可以表示为

3 修正线圈匝数分布函数

根据假设③，线圈匝数分布函数被视为阶跃函数。MWFA 计算得到的气隙磁通密度曲线在定子槽开口处与FEA 拟合结果较差，为解决此问题，需要对线圈匝数分布函数进行修正。

励磁绕组线圈匝数与机械角度之间的关系定义为线圈匝数分布函数，用nexc(ϕ)表示。正弦绕组和余弦绕组的线圈匝数函数分别用nsin(ϕ)和ncos(ϕ)表示。本节主要描述励磁绕组线圈匝数分布函数的修正过程。为便于表述，修正励磁绕组线圈匝数分布函数时，将不展示正弦绕组和余弦绕组。

未经修正的励磁绕组线圈匝数分布函数如图4中 的nexc(Con)所 示， 当ϕ的 取 值 范 围 为[(2i–3)ϕt/2+(i–1)ϕs]～[(2i–1)ϕt/2+(i–1)ϕs]，且定子齿标号i取奇数时，nexc(Con)(ϕ)为

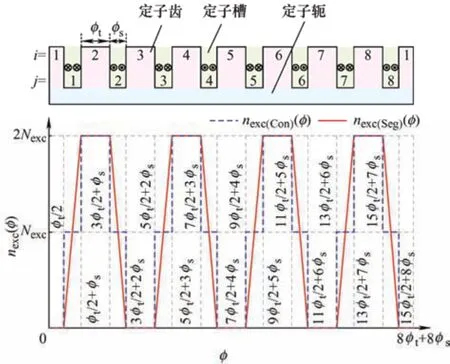
图4 定子展开图及修正前后的线圈匝数分布函数

当定子齿标号i取偶数时，nexc(Con)(ϕ)为

当ϕ的取值范围为[(2j–1)ϕt/2+(j–1)ϕs]～[(2j–1)·ϕt/2+jϕs]时，其中j为定子槽标号，nexc(Con)(ϕ)为

定子展开图以及修正前后的励磁绕组线圈匝数分布函数如图4 所示，其中绕组函数过渡区域为ϕs。

从图4 可以看出，定子槽中两个励磁绕组的极性相同，而相邻两个槽中绕组的极性则不同。以第1、2 号两个定子槽为例，分析线圈匝数分布函数的表达式。线圈匝数在第一个定子槽的位置开始逐渐增加，虽然第二个槽中的线圈匝数也增加了，但由于极性不同，表现在线圈匝数分布函数中便是匝数逐渐减少。其他六个槽也以这种方式依次分析。考虑到这些因素，将图4 中的线圈匝数分布函数nexc(Con)(ϕ)修改为nexc(Seg)(ϕ)。

只有当ϕ的取值范围为[(2j–1)ϕt/2+(j–1)ϕs]～[(2j–1)ϕt/2+jϕs]时，nexc(Seg)(ϕ)的表达式与nexc(Con)(ϕ)不同，其余范围均相同。

由MWFA 计算得到的气隙磁通密度为

式中，M(Con)(ϕ,θ)为线圈匝数分布函数未修正分段时的改进绕组函数。

仅修正线圈匝数分布函数之后的气隙磁通密度为

式中，M(SegO)(ϕ,θ)为只修正线圈匝数分布函数时的改进绕组函数。

当转子位置θ=0、励磁电流iexc=0.05 A 时，气隙磁通密度计算结果如图5 所示。在槽开口处，通过MWFA 计算的气隙磁链密度为恒定值，显然与FEA 的计算结果不符。而修正线圈匝数分布函数后的计算结果Br(SegO)与Br(FEA)非常接近，充分证明对线圈匝数分布函数进行修正的有效性。

图5 转子位置θ=0、励磁电流iexc=0.05 A 时，气隙磁通密度波形计算对比

4 修正气隙函数

在之前的工作中，通过MWFA 计算得到的励磁绕组自感在完整机械周期中为恒定值，虽然其平均值与FEA 计算结果较为吻合，但波形仍有出入。为解决此问题，本节将考虑假设④中提到的槽开口影响，并修正气隙函数。

未修正时的气隙函数用g(Con)(ϕ,θ)表示为

定子槽内及其附近气隙处的磁通分布如图6 所示。由图6 可以看出，在槽开口处仍有部分磁通通过气隙，因此应考虑槽开口的影响。定子槽的尺寸如表2 所示。

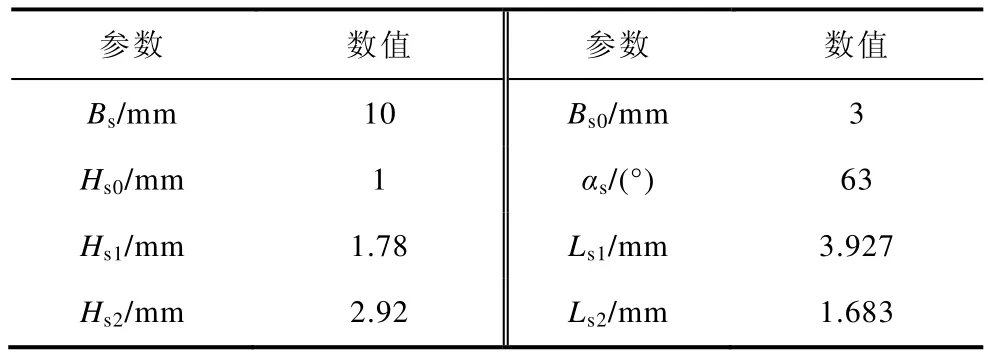
表2 定子槽尺寸

图6 定子槽内以及槽开口附近的磁场分布

为了使计算结果更加准确，槽开口处气隙长度应充分考虑磁场分布和定子槽开口的影响，而定子齿处的气隙长度则应保持不变。因此，修正后的气隙函数为分段函数。分段的气隙函数用g(Seg)(ϕ,θ)表示

式 中，ϕ的 取 值 范 围 为[(2j–1)ϕt/2+(j–1)ϕs]～[(2j–1)ϕt/2+jϕs]，j为定子槽标号。

当转子位置θ=0 时，气隙函数如图7 所示，其中g(Con)和g(Seg)分别表示修正前后的气隙函数。

图7 当转子位置θ=0 时，修正前后的气隙函数

可见，所提方法是在常规计算方法的基础上，对线圈匝数分布函数和气隙函数进行了分段修正，因此将所提方法定义为分段绕组函数法(Segmented winding function method，SWFM)。

由SWFM 计算出的气隙通量密度为

式中，M(SegA)(ϕ,θ)为将线圈匝数分布函数和气隙函数同时分段时的修正绕组函数。

当转子位置θ=0、励磁电流iexc=0.05 A 时，采用SWFM计算得到的气隙磁通密度波形Br(SegA)如图8 所示。由图8 可以发现，解析得到的气隙磁通密度在定子槽开口处与FEA 结果的吻合程度明显改善，且Br(SegA)与Br(FEA)曲线在整体上吻合良好，充分验证了所提出方法的有效性。

图8 转子位置θ=0、励磁电流iexc=0.05 A 时，所提SWFM 方法有效性验证

采用MWFA 计算的励磁绕组电枢自感为

采用SWFM 计算的励磁绕组电枢自感为

在此基础上，进一步考虑漏感，可以得到励磁绕组自感。由之前工作可知，解析计算得到的励磁绕组自感直流分量与FEA 非常接近，相对误差约为1%；而交流分量则误差较大。因此，提取MWFA和SWFM 计算得到的励磁绕组自感交流分量，对比如图9 所示。从图9 可以看出，修正线圈匝数分布函数和气隙函数后，励磁绕组自感交流分量幅值相较于常规MWFA 更为准确，且其相位与FEA 结果一致，进一步验证了所提方法的有效性。

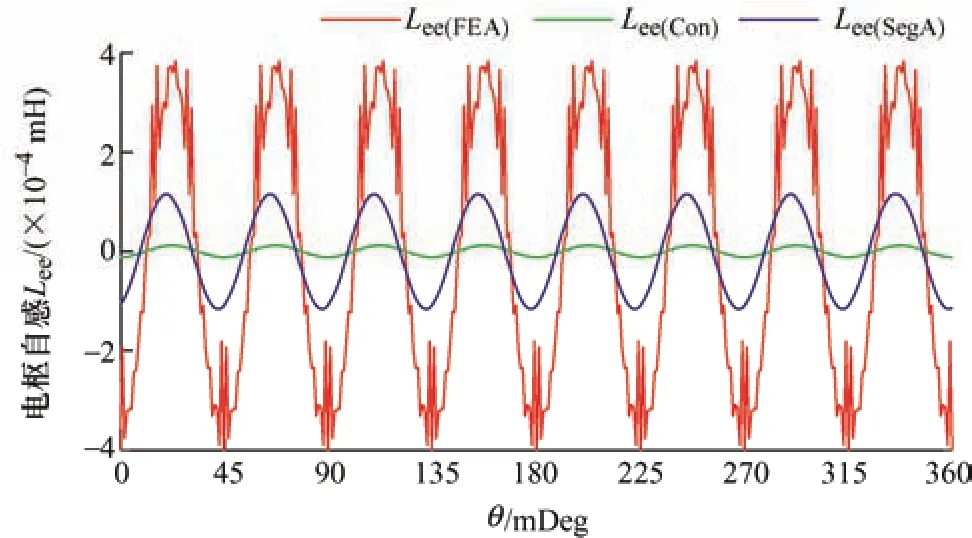
图9 励磁绕组自感交流分量对比

5 结论

在MWFA 基础上，通过修正线圈匝数分布函数和气隙函数，本文提出了分段绕组函数法，用于分析VRR 的气隙磁通密度和励磁绕组自感，并将SWFM、传统MWFA 方法的计算结果与FEA 结果进行对比，得到如下结论。

(1) MWFA 未能较好考虑槽开口对气隙磁密的影响，导致解析计算的气隙磁密在槽开口处存在突变。

(2) 受槽内导体分布和槽开口影响，励磁绕组自感存在周期性脉动，MWFA 亦无法体现。

(3) 采用SWFM 计算得到的气隙磁密和电感波形更为精确丰富，与FEA 计算得到的波形拓扑更为吻合。