三相电压型PWM 整流器的模型预测滑模控制*

徐 鹏 苏 鑫 郭 铖 袁利兵 但远宏

(1.重庆理工大学电气与电子工程学院 重庆 400054；2.重庆理工大学计算机科学与工程学院 重庆 400054；3.南京理工大学瞬态物理国家重点实验室 南京 210094)

1 引言

全球环境恶化，我国提出了碳达峰、碳中和的战略目标[1]。目前清洁能源被广泛关注，如风电、水利发电和光伏发电。三相电压型PWM 整流器因其具有高功率输出、低谐波线电流、直流链路电压可调节等特点[2-3]，目前被广泛应用于新能源汽车[4-5]、海上风力发电[6-7]、直流输电系统[8-9]等。

目前已有许多的控制策略应用在整流器上，如电压定向矢量控制(Voltage oriented control, VOC)、自抗扰控制(Active disturbance rejection control,ADRC)、滑模变结构控制(Sliding mode control, SMC)和模型预测控制(Model predictive control, MPC)等都得到了广泛的研究。文献[10]对电压矢量控制进行了研究，通过坐标变换建立数学模型设计了双闭环PI 控制，验证了算法的可行性，但PI 控制的参数整定困难，对于外部干扰不能快速地跟踪难以达到较好的控制效果。文献[11]提出了预测直接功率控制，针对功率跟踪偏差问题设计了优化模型，并使用空间矢量调制实现定频率控制。文献[12]针对数字处理延迟问题，设计两步预测消除延迟，同时设计了消除功率偏差校正环节和无网压传感器算法减少了耗费成本。文献[13]结合预测控制算法提出改进滑模控制和死拍预测直接功率控制的复合算法，提高了系统的响应速度和抗干扰的能力。文献[14-15]针对外部干扰设计了线性自抗扰控制，利用观测器进行扰动补偿提升了系统鲁棒性。文献[16]针对脉冲负载设计了自适应自抗扰控制，通过自适应与自抗扰结合对其参数调节，提高了系统的动态响应速度，降低了稳态时网侧电流谐波，但自抗扰控制器参数较多，参数整定较为困难。文献[17]提出了高阶积分端末滑模控制和高阶滑模趋近律，有效降低了系统稳态误差和滑模面的抖振。文献[18]提出了滑模观测器和滑模控制结合的控制策略，提高了整流器直流电压抗干扰能力和运行时网侧电流的稳定性，使其能在多工况下正常运行。文献[19]针对五电平整流器的传统模型预测动态性能差的问题，提出滑模模型预测控制，提升了整流器动态响应速度和抗干扰性能。文献[20]针对传统模型预测功率控制的预测目标不精确，存在电压波动较大的问题，提出了优化模型预测功率，同时电压外环采用自适应模糊控制，优化后显著提升了系统的稳态性能和动态抗干扰性，但是该控制策略的算法较复杂，计算量大，实用比较困难。

综上所述，针对传统模型预测PI 控制(Model predictive PI control, MPPIC)存在寻优过程计算复杂、动态响应速度较慢、抗干扰的能力较差等问题，本文设计了优化的模型预测控制和滑模变结构控制相结合的模型预测滑模控制(Model predictive sliding mode control, MPSMC)算法。首先，通过对三相电压型PWM 整流器的拓扑原理分析，得出了其控制数学模型。然后，针对传统有限集模型预测控制的遍历寻优计算复杂的问题，采用无差拍控制原理简化了模型预测寻优次数。之后，针对传统PI 控制动态响应较慢、抗干扰能力较差的问题，外环设计了快速幂次趋近率的积分滑模控制。最后，对提出的MPSMC 和传统的MPPIC 进行了仿真和试验对比，验证了所提算法的可行性和有效性。

2 三相电压型PWM 整流器数学模型

图1 为三相电压型PWM 整流器主电路结构。主电路采用对称三相三线制，6 个绝缘栅双极管(Insulated gate bipolar transistor, IGBT)和6 个二极管反并联的方式。图1 中，ea、eb和ec分别为三相对称交流侧电源电压；Va、Vb和Vc分别为整流器输入侧三相电压；ia、ib和ic分别为三相交流电流；R和L分别为线路等效电阻参数和进线电感等效电感参数；C为直流滤波电感等效参数；RL为直流负载等效阻值参数，Vdc为直流侧电压。

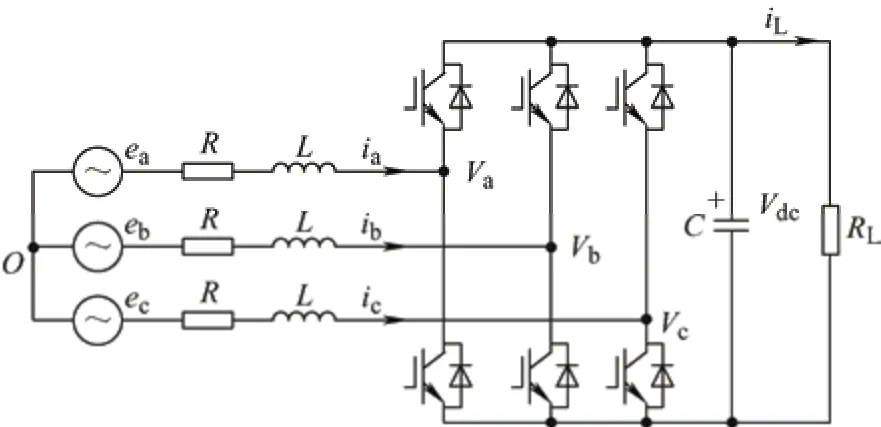
图1 三相电压型PWM 整流电路原理图

由基尔霍夫电压定律和电流定律，建立每相回路方程，得到三相电压型PWM 整流器的数学模型，其表达式为

式中，iL为负载电流；Sa、Sb和Sc分别为开关的开关状态。

为了便于分析，将开关的状态定义为开关函数

式中，k代表a，b，c 相。

通过坐标变换将三相的开关状态转换到两相静止坐标系中

将三相VSR 的数学模型转换到两相静止坐标系中

式中，eαβ为电网电压矢量；iαβ、Vαβ分别为输入电流矢量和电压矢量。

结合上述分析，三相VSR 的动态模型用αβ轴分量表示为

由空间电压矢量原理可得，输入电压矢量可由固定的αβ轴坐标系上的8 条电压空间矢量表示，如图2 所示。其中V0与V7为零电压矢量。

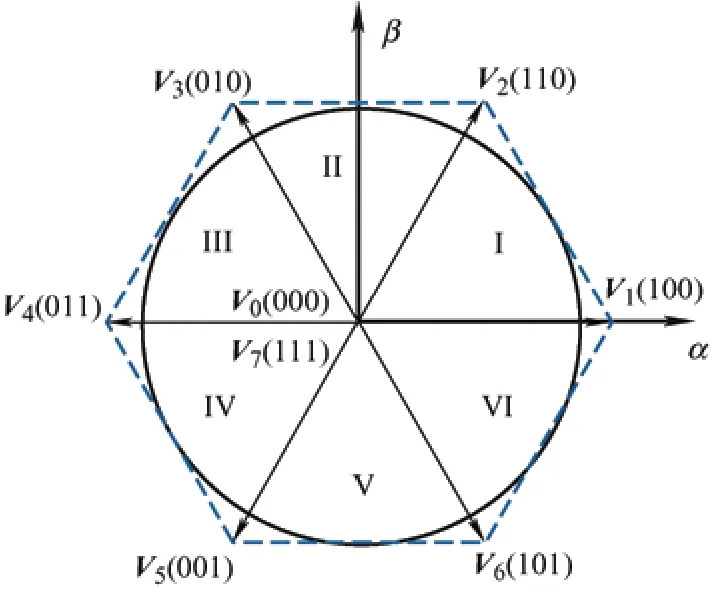
图2 αβ 轴坐标系空间矢量扇区

3 模型预测控制器的设计

3.1 整流系统结构框图

如图3 所示为模型预测PI 双闭环控制系统的结构图。外环PI 控制得到有功功率参考值，为了实现单位功率因素运行，无功功率设置为0 Var。内环输入两相静止坐标系下的电压Vαβ、电流iαβ，通过三相电压型整流器的离散预测模型，预测计算出8 条电压矢量作用下的输入功率，通过代价函数选择最优的开关状态作为下一时刻功率变换器的控制信号。

图3 模型预测PI 控制结构框图

3.2 模型预测控制器

预测控制可以实现输出电压控制，还能控制有功功率和无功功率控制达到期望值。设系统采样时间为Ts，在k+1 时刻，网侧电流的离散模型可表示为

由此，可以计算出系统的有功功率和无功功率

控制有功功率和无功功率，建立成本函数

式中，Pref、Qref分别为有功功率和无功功率参考值。

传统的有限集模型预测控制通过遍历寻优，每个控制周期会对8 个电压矢量进行比较选取最优电压矢量，然后输出其对应的开关序列控制IGBT 工作。这种方式寻优准确度较高，但需要计算8 个电压失量对应的电流进行功率计算寻优比较，计算量较大，控制效果较差。为了减少寻优次数，本文设计了优化的模型预测控制算法，将每个控制周期8次寻优减少到3 次，提高了系统稳态性能。

由无差拍控制理论可得，本文目标控制有功功率和无功功率误差值最小。设有功功率和无功功率误差为零，即有

将式(8)、(9)代入式(11)可得

如表1 所示，每一个扇区都由两个非零电压矢量和一个零电压矢量合成，将最优电压矢量与所在扇区相邻的两个非零电压矢量和零电压矢量代入代价函数

表1 扇区和电压矢量关系表

式中，Vα*、Vβ*分别为α、β轴上的最优电压参考值。通过代价函数可以选取出该扇区最接近参考电压矢量的最优电压矢量，然后输出对应的开关序列。

4 滑模控制器设计

4.1 滑模控制律设计

如图3 所示，传统的控制系统外环有功功率参考值由PI 控制器得出，PI 为线性控制策略，当系统参数和运行状态变化时，系统的动态性能跟踪速度比较缓慢。相对而言，滑模控制更符合非线性系统，因控制器到达滑模面后对系统参数不太敏感而具有较强鲁棒性，动态性能较好。因此为了提高系统的动态性能，将外环改用滑模控制器。

由图1 所示三相电压型PWM 整流电路原理图，建立直流侧瞬时功率方程

根据功率守恒定律，整流器的输入瞬时功率等于输出瞬时功率。为便于分析，本文忽略整流器的功率损耗。

为了实现输出电压跟踪期望电压值，跟踪误差e可表示为

为了使控制稳态误差为零，根据滑模变结构控制原理，设计了电压误差的比例积分滑模面

式中，c1>0，c2>0，对滑模面求导将式(15)代入得

为了改善系统到达滑动模态的性能，采用快速幂次趋近律来设计电压外环控制器，即

式中，k1>0，k2>0，0<α<1，sgn 为符号函数，通过α值的调整，可以保证当系统状态远离滑模面时，能够较快地趋近于滑动模态，当系统状态趋近滑模面时，保证较小的控制增益，以达到较小抖振的效果。

由式(15)、式(18)和式(19)可得

进一步转化得

通过上式得出了滑模控制器的控制律和参考功率Pref。考虑到三相整流器实际复杂工况，采用饱和函数sat(s)代替不连续的sgn(s)符号函数以削弱抖振。

式中，Δ为边界层厚度且Δ>0，替换开关函数后可将式(21)改写为

4.2 滑模存在条件证明

滑模存在条件是设计滑模控制的前提，为了保证滑模面附进的轨迹点都能在有限的时间到达滑模面，对其滑模的存在条件证明。

选取李雅普诺夫函数为

对式(24)求导并将式(19)代入，可得

如果到达点在所创建开关面的领域中处于正位置，即s>0。则有

如果到达点在所创建开关面的领域中处于负位置，即s<0。则有

由式(27)和式(29)可以得出结论，满足滑模的存在条件。

5 仿真及实物试验验证

5.1 仿真结果与分析

为了验证三相电压型PWM 整流器模型预测滑模控制策略的有效性，通过Matlab/Simulink 搭建了仿真平台，其所用参数如表2 所示。

表2 三相电压型PWM 整流器的参数

图4 为启动响应直流电压波形，两种控制方法都能将输出电压控制到参考值，其中MPPIC 输出电压在48 ms 到达给定稳态值，而MPSMC 输出电压到达给定稳态值的速度较MPPIC 快很多，仅用了20 ms。MPSMC 输出电压到达给定稳态值的过程比较平滑且几乎没有出现电压超调，而MPPIC 输出电压到达给定稳态值的过程中存在18 V 的电压超调。

图4 启动响应直流电压波形

图5 为稳态a 相电压电流波形，两种控制都能使整流器的交流侧电流和电压同相位，实现了单位功率因素运行，其中MPSMC 的电流波形更为平滑。图6 为a 相输入电流总谐波含量，通过快速傅里叶变换分析得出，MPPIC 的电流总谐波(Total harmonic distortion, THD)含量为4.11%，MPSMC 的THD 为2.63%，两种控制的电流谐波含量都满足国家对谐波总含量不超过5%的要求，其中MPSMC 总谐波含量更低，提高了网侧电流质量。

图5 稳态a 相电压电流波形

图6 a 相输入电流总谐波含量

当系统运行到0.1 s 时突变负载，将直流侧负载电阻从40 Ω 突减到20 Ω，图7 为突变负载直流电压波形，图7a 中MPPIC 和MPSMC 的直流电压都有跌落，然后在有限时间内又恢复到给定参考值，其中MPPIC 的恢复时间约为120 ms，电压跌落约为36 V，而MPSMC 的恢复时间约为14 ms，电压跌落约为2.2 V。可以看出MPSMC 具有较强的抗负载扰动性能，能更快跟踪负载的突变。同时为了验证本文提出的外环滑模的控制性能，将外环采样指数趋近律滑模的MPSMC-IC 和MPSMC 进行对比，图7b 中MPSMC-IC 负载突变电压的恢复时间为22 ms，但电压跌落为3.8 V，MPSMC 的恢复时间约为14 ms，电压跌落约为2.2 V；MPSMC 静态误差和抖振幅度较MPSMC-IC 更小，可以看出MPSMC 的外环滑模降低了静态误差，减小了系统的抖振。

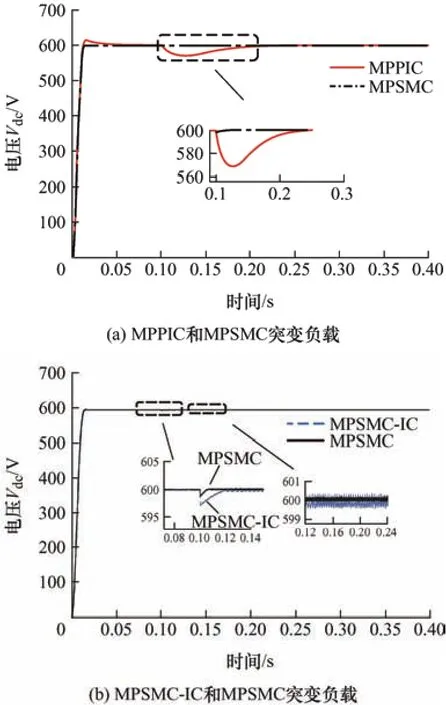
图7 突变负载直流电压波形

综上所述，MPSMC 和MPPIC 都能控制整流器单位功率因数运行，MPSMC 减少了电流谐波，具有更好的稳态性能；在启动响应和突变负载响应时，MPSMC 较MPPIC 具有更快的跟踪速度和更强的抗负载干扰等特性，提高了整流器的运行性能，为后续进行实物控制设计提供了理论依据。

5.2 实物试验结果与分析

为了验证设计的MPSMC 算法的可行性，基于以上理论分析搭建了小功率的三相整流器的试验平台。DSP 采用德州仪器(TI)公司的TMS320F28335处理芯片，IGBT 采用安森美公司的FGH40N60UFD型号。由于试验条件受限，实物参数设计如下：交流输入电压幅值为40 V，直流侧输出电压为150 V，滤波电容和电感和仿真参数保持一致，直流侧负载为75～150 Ω，采样周期为50 μs。

图8 为启动响应直流电压波形，整流器由不控整流状态然后启动控制器，电压到达给定参考电压。可以看出MPPIC和MPSMC到达稳态电压的时间分别为400 ms 和200 ms，MPPIC 存在8 V 电压过冲，MPSMC 的启动速度更快，电压更为平滑且未出现过冲现象。

图8 启动响应直流电压波形

图9 为整流器稳态运行时网侧相电压电流波形，可以看出两种控制下电压和电流相位保持一致，波形均为正弦波，都实现了单位功率因素运行，其中MPSMC 的电流波形更加平滑。

图9 稳态时网侧a 相电压电流波形

图10 为负载突变试验波形，直流负载电阻首先由150 Ω 跳变为75 Ω 然后又跳变为150 Ω，采用MPPIC 策略时，负载突减后直流电压经过320 ms 电压跌落后重新回到给定电压值，负载突增后直流电压经过300 ms 电压超调后恢复到给定电压值。采用MPSMC 策略时，负载突减后直流电压经过120 ms电压跌落后重新回到给定电压值，负载突增后直流电压经过120 ms 电压超调后恢复到给定电压值。验证了MPSMC 在负载突变时具有更好的抗干扰能力。

图10 负载突变试验波形

6 结论

针对传统的模型预测控制寻优过程复杂，导致静态性能较差；外环的PI 控制不能快速跟踪系统状态变化，导致抗干扰能力较差等问题，提出了MPSMC 控制策略。该方法将模型预测控制和滑模控制结合，极大地提高了三相电压型PWM 整流器的控制性能。仿真和试验表明，与传统模型预测控制策略相比，本文所提控制策略具有以下特点。

(1) 简化了寻优次数，提升了系统稳态性能，降低了网侧的电流谐波，实现了单位功率因数运行。

(2) 采用外环积分滑模控制器的设计，系统能够更快地跟踪动态变化，提升了系统的抗干扰能力。