考虑参数失配的永磁同步电机电流预测控制研究*

顾子杰 卜飞飞 张得礼 董兆鹏 徐振缘 孙鹏宇

(1.南京航空航天大学自动化学院 南京 210016；2.南京航空航天大学机电学院 南京 210016)

1 引言

永磁同步电机因其特有优势在高性能伺服领域得到越来越多的应用，具体特点包括功率密度大、效率高、体积小、过载能力强等。严苛的运行环境与高标准的控制精度对永磁同步电机的控制策略提出了更高要求，其中电机电流内环的控制性能直接影响了永磁同步电机的动态响应速度与稳态控制精度等，因此，考虑到电流环控制策略在高性能伺服领域的关键影响，国内外专家学者对于电流控制方法展开了大量深入的研究。常见的电流控制策略包括滞环控制、无差拍电流预测控制、模糊控制、神经网络控制等。文献[1]通过改进的滞环控制策略在保证永磁同步电机直接转矩控制系统良好的静、动态性能的前提下，提高了系统的抗扰性能，但其开关频率不固定，输出谐波分散，滤波器设计困难。文献[2]采用了一种非级联结构的无差拍电流预测控制策略，舍弃了转速环PI 控制器，极大程度提高了转速动态响应速度，但其方法在面对相对复杂的电机模型时，电流工作点求解难度高。文献[3]通过引入模糊前馈控制器，大大降低了无差拍电流控制系统的参数敏感性，提高了系统的抗干扰性与鲁棒性，但在突加负载时d轴与q轴电流会产生较大超调。文献[4]通过径向基(Radial basis function，RBF)神经网络对永磁同步电机在线辨识，进而实现电流内环控制器参数整定，仿真结果证明其RBF-PID 控制策略拥有更快的响应与良好的抗干扰能力，但提高响应速度的同时带来了更大的转速超调。其中，电流预测控制策略具有动态响应快、控制精度高的特点，且其控制效果仅依赖于少量电机电气参数，系统结构设计简单，得到了广泛关注。

电流预测控制策略的控制效果极大程度上受采样误差影响，即信号的采集延时与数字处理器的计算延时[5-7]，除此以外，电流预测控制策略作为一种基于模型的控制方法，其对于电机本身电气参数的敏感性不可忽略，而被控永磁同步电机在高性能伺服控制环境中，例如机电作动伺服领域等高强度、长时间运行下，其实际参数会产生客观变化[8-9]。文献[10-12]指出，在参数失配的情况下，电流预测控制会出现较大的电流预测误差，使电流控制失稳，系统鲁棒性差，因此，众多专家学者对于电机参数辨识策略展开了相关研究。文献[13]采用了一种结合自适应正态云模型的樽海鞘群辨识算法进行电机参数在线辨识，避免陷入局部最优且收敛精度高，但其算法复杂且存在辨识静差。文献[14]提出了一种混沌映射与信息传递相结合的混沌遗传粒子群算法，结合分步辨识与循环更新解决了参数欠秩问题且拥有较低的参数辨识误差，但未考虑逆变器死区时间的影响，导致辨识结果不够准确。文献[15]提出了一种基于有效信息迭代的快速粒子群优化算法对永磁同步电机进行参数辨识，通过迭代有效电机参数信息和增添新的迭代终止条件改进标准粒子群优化算法的收敛快速性，虽然降低了系统算法计算量但辨识精度不高。文献[16]提出了一种基于扩展卡尔曼滤波的在线参数辨识方法，通过转动惯量实时更新电感与磁链的辨识结果，所设计系统的辨识误差小于1%，但其辨识效果受转动惯量获取准确性的限制。

本文以永磁同步电机伺服驱动系统模型为基础，提出了考虑参数失配的电流两步预测控制策略，弥补了控制系统采样延时与数字处理器的计算延时，通过模型参考自适应的辨识策略实现了对永磁同步电机伺服驱动系统电机运行参数的准确、快速辨识，对于提高基于电流预测控制策略的永磁同步电机伺服驱动系统的电流控制精度与系统鲁棒性具有重要意义。

2 永磁同步电机数学模型

对于永磁同步电机，其在d-q旋转坐标系下的数学模型如式(1)所示

式中，ud、uq分别为d-q轴电压矢量分量；id、iq分别为d-q轴电流矢量分量，Rs为定子电阻，Ld、Lq为d-q轴电感，ωe为电机电角速度，Ψf为永磁体磁链，考虑到本文的研究对象为表贴式永磁同步电机，对于d-q轴电感有

根据式(1)与式(2)，选择d-q轴电流为状态变量，可以得到被控对象的状态方程为

3 两步预测的电流环控制策略

3.1 系统延时分析

通过电流预测控制算法能够在不进行复杂调节器参数整定的情况下，获取更快的电流响应，而在实际数字控制系统中，其控制效果受电流采样延时、脉宽调制(Pulse width modulation，PWM)占空比更新延时等环节的影响[17]，如图1 所示。

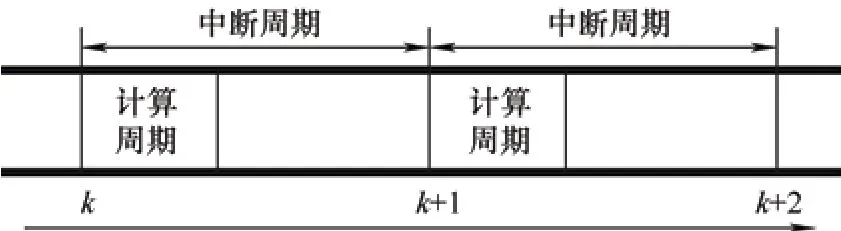
图1 数字控制系统延时时序图

k时刻计算得到的电压矢量经过一个采样周期才能实现逆变器加载，即k+1 时刻，而该加载电压矢量作用产生的电压电流信号在k+2 时刻才能完成采集，该延时的存在直接导致了电流预测误差较大，甚至导致系统失稳，因此本文采用了电流两步预测控制策略。

3.2 电流两步预测控制策略

对式(1)进行离散化，得到k+1 时刻的电流为

根据前文对于数字控制系统延时的分析，需要对k+2 时刻的电流进行预测，并以此电流值作为k+1时刻电流采样值的替代，通过两步预测完成控制策略的延时补偿，在预测k+2 时刻的期望电压时，由于相邻控制周期的时间间隔极小，可以将电机参数与转速视为恒值，因此k+2 时刻的电压预测方程为

在系统延时得到补偿后，实现了k+2 时刻的电流实际值对于电流给定值的无差跟踪，即

式中，为电流给定值。

由式(4)与式(5)计算可得两步预测控制下的控制电压矢量为

由控制策略推导过程可知，电流两步预测控制策略所需参数仅涉及电机永磁体磁链、定子电阻等已知参数，避免了传统控制器繁琐的参数整定，易于实现与应用。

4 参数失配与参数辨识策略

4.1 参数失配

虽然通过电流两步预测算法能够在不进行复杂控制器参数整定的情况下，实现永磁同步电机伺服驱动系统控制性能的优化，但由上文推导的预测控制策略可知，电机参数的准确性将对控制效果产生直接影响，随着电机运行温度变化，铁磁材料的磁导率也将随着温度变化而出现非线性变化，进而导致磁链与电感参数的变化，尤其是在电机功率密度较高的应用领域，电机温度变化范围大，受其影响，电枢电阻与永磁体材料会出现较大范围的变化。因此，参数失配问题极大限制了电流预测控制策略的控制效果与应用环境。

4.2 参数辨识策略

由式(7)可知，电阻Rs、磁链fψ、电感Ls若存在参数失配将对电流两步预测控制策略产生直接影响，电感参数失配与控制系统的动态性能与稳定性降低密切相关，磁链参数失配主要影响了q轴电流的稳态误差，而电阻误差的影响并不明显，其参数误差在实际应用中可以忽略不计[18-20]，因此本文将基于模型参考自适应策略对电机磁链与电感进行参数辨识策略研究。

图2 为模型参考自适应策略原理框图，主要结构包括参考模型、可调模型与参数自适应律，三者共同组成了能够实现参数实时动态反馈的自适应结构，其中，参考模型不包含待观测量，而可调模型包含待观测量。在同一信号u的输入作用下，自适应律将进行快速调节，直至参考模型与可调模型在相同输入下的输出偏差为0 时，可调模型中的参数为最佳辨识值。

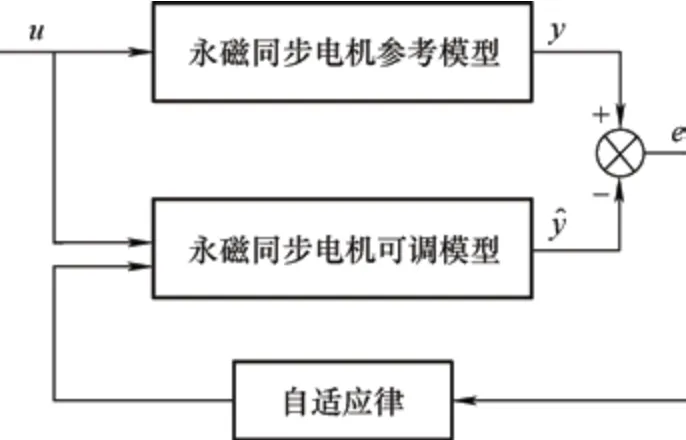
图2 永磁同步电机两步预测控制策略框图

目前，常用自适应律设计准则主要包括MIT 自适应律、基于Lyapunov 稳定性理论的设计准则与基于Popov 超稳定性理论的设计方法。由于采用Popov超稳定性理论进行自适应律设计能够兼顾系统稳定性与设计便捷性，因此本文采用该设计准则实现参数自适应律设计。

令i，由式(3)可得参考模型为

由式(8)得到可调模型为

定义广义误差e=i，由式(8)、式(9)作差得到

为了满足该系统的全局稳定，由Popov 超稳定性理论可得

式中，0r为不随时间变化的正常数，t0>0 。

一般情况下，为使广义误差等于0 时，调节作用仍然起效，采用如下的比例积分形式对自适应律进行设计

将e与w代入Popov 积分不等式，推导可得、的自适应律为

式中，kpa、kpb为相应自适应参数的比例系数，kia、kib为相应自适应参数的积分系数，与为参数的初始值。

通过第3、4 节的两步电流预测与考虑参数失配的控制策略设计，得到系统控制框图如图3 所示。

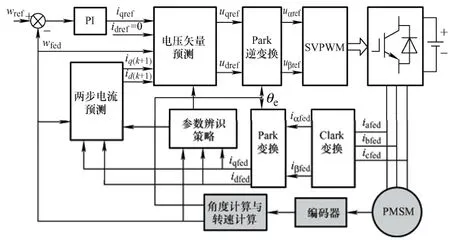
图3 考虑参数失配的永磁同步电机电流预测控制策略框图

5 仿真分析

为了验证上述分析与研究策略的有效性与可行性，在Simulink 中搭建了仿真模型进行验证，所采用的永磁同步电机参数设置如表1 所示。

表1 永磁同步电机参数

电机以1 000 r/min 的转速空载阶跃起动，在0.2 s 时刻突加负载。令电流预测模型电感参数为电机实际电感参数的两倍，图4 为电感参数失配条件下q轴电流的响应波形；令电流预测模型磁链参数为电机实际磁链参数的两倍，图5 为磁链参数失配条件下的q轴电流响应波形。

图4 电感参数失配条件下q 轴电流响应波形

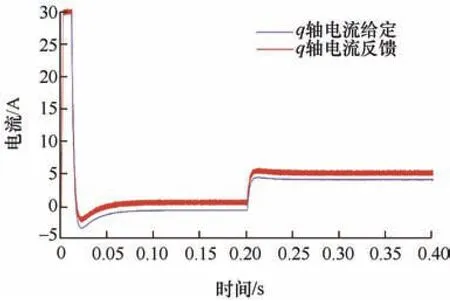
图5 磁链参数失配条件下q 轴电流响应波形

由图4 可知，电感参数的失配会导致较大的电流预测误差，电流稳态控制性能差；而磁链参数失配虽然未影响电流反馈的稳态性能，但会导致电流反馈值小于电流给定值，使得电流反馈出现静差。

因此采用本文提出的模型参考自适应策略对永磁同步电机磁链与电感参数进行辨识。

使电机以1 000 r/min 的转速空载阶跃起动，确保参考模型参数与电机真实值一致，基于模型参考自适应算法的磁链与电感辨识波形分别如图6 与图7 所示，磁链与电感辨识值均在30 ms 内收敛于真实值附近，磁链稳态辨识误差约为1.9%，电感辨识误差约为1.4%，仿真结果说明，在电机稳态运行时，本文提出的参数辨识策略所观测的电机参数能够迅速收敛至真实值，取得了良好效果。

图6 电机磁链参数辨识波形图

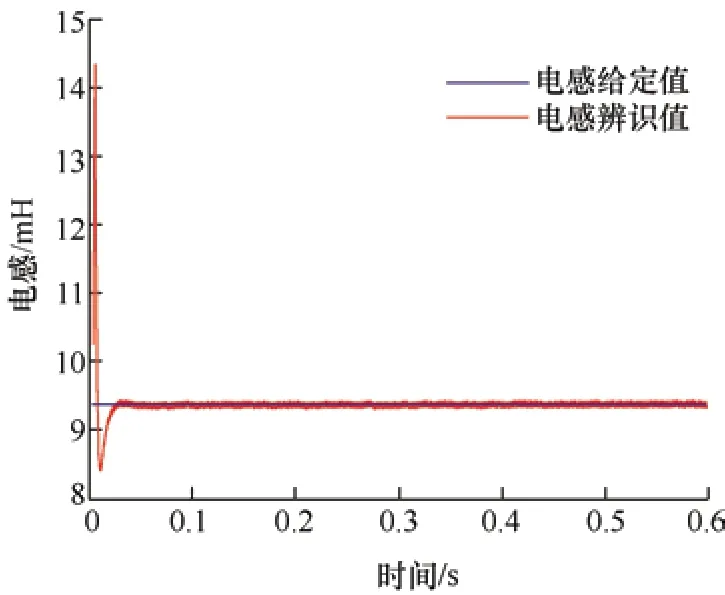
图7 电机电感参数辨识波形图

考虑到电机突加突卸负载时，电流的给定值在电机机械时间常数的限制下响应缓慢，不易突显控制策略的快速性与跟随特性，因此主要针对转速突变下q轴电流响应情况进行仿真。在仿真软件中，设置电机的给定转速为1 000 r/min 且空载阶跃起动，并于0.08 s 时突降转速至700 r/min。

如图8 所示为传统PI 控制策略下永磁同步电机q轴电流响应波形，图9 所示为考虑参数失配的电流预测控制策略下永磁同步电机q轴电流响应波形，在0.08 s 发生转速突减时，本文所提预测控制策略能够快速且准确地跟踪上电流指令，而在传统PI 策略下面对给定电流突变，反馈电流未能实现准确跟踪且响应速度较慢；在稳态阶段，传统控制策略的电流反馈波形出现了电流振荡，电流纹波较大，而本文所提的电流预测控制策略拥有更小的电流纹波，具备良好的稳态性能。

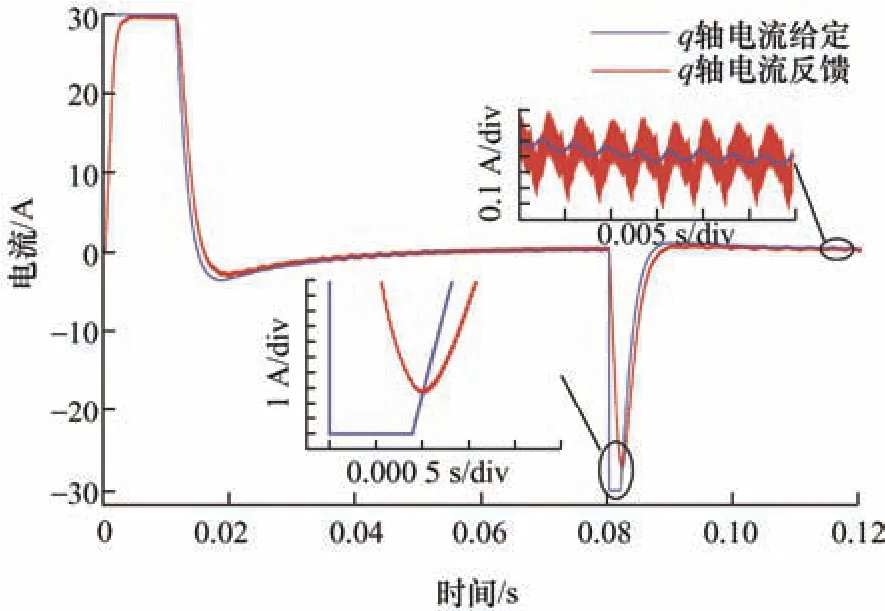
图8 传统PI 控制策略下永磁同步电机q 轴电流响应波形

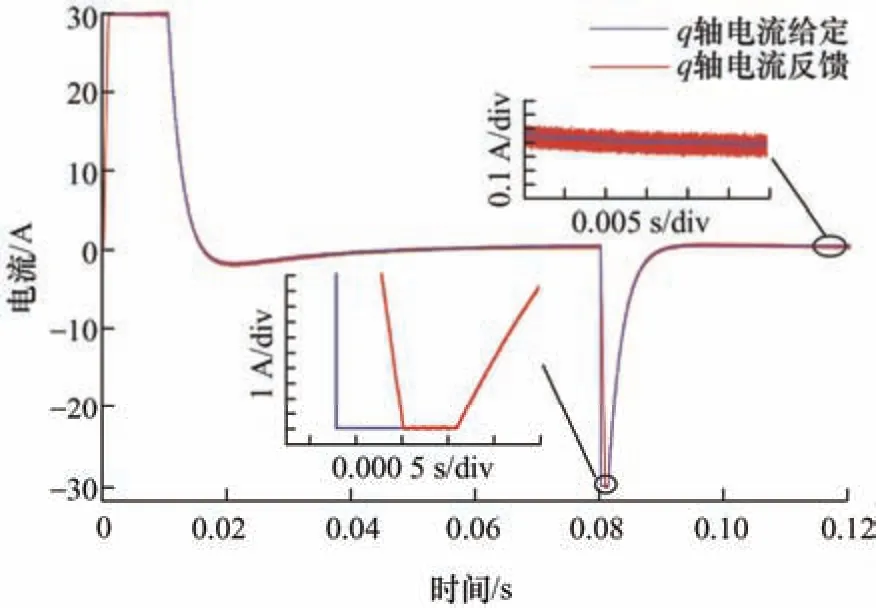
图9 考虑参数失配的电流预测控制策略下永磁同步电机q 轴电流响应波形

使电机以1 000 r/min 的转速空载阶跃起动，并在0.3 s 时突加负载，图10、图11 分别为传统PI控制策略与本文所提电流预测控制策略的三相电流仿真波形。

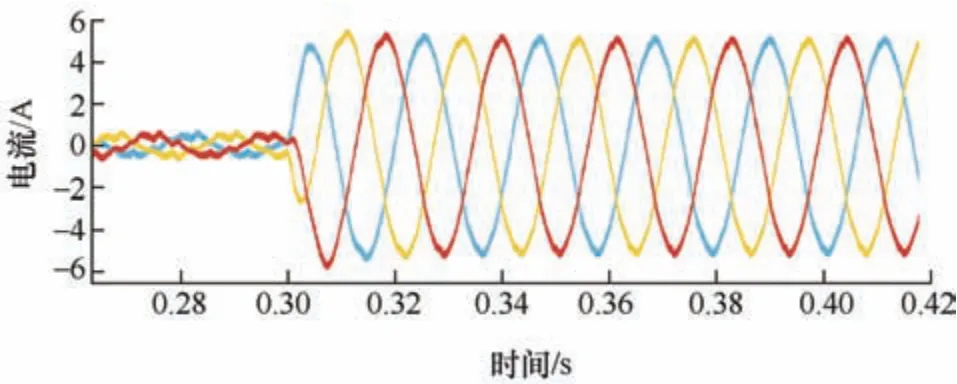
图10 传统PI 控制策略下永磁同步电机三相电流波形

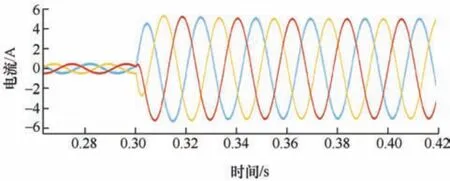
图11 考虑参数失配的电流预测控制策略下永磁同步电机三相电流波形

由图10 可知，传统PI 控制策略下的三相电流波形会发生不同程度的畸变，在加载过程之前，三相电流较小，而畸变程度较大，在0.3 s 对电机进行加载后，三相电流突增，但仍存在电流畸变现象；而由图11 可知，本文提出的考虑参数失配的电流预测控制策略在电机加载前后输出的三相电流正弦波效果更优，能够对电流畸变进行有效抑制。

6 结论

为了实现永磁同步电机伺服驱动系统电流内环的优化设计，克服传统控制器参数整定繁琐且性能较差的问题，本文以永磁同步电机模型为基础，通过电流两步预测控制策略进行电流控制器设计，对考虑参数失配的改进电流预测控制策略展开研究与验证，得到如下结论。

(1) 通过提出的模型参考自适应辨识策略能够对电机参数进行快速、准确辨识，为永磁同步电机电流预测控制策略下存在的参数失配问题提供了有效解决途径。

(2) 针对数字系统延时对于电流预测控制策略预测误差的影响，采用了两步预测的控制方法，与参数辨识策略相辅相成，在保证电流控制响应快速性的同时，获得了良好的电流跟随特性与稳态特性。