传输线方程高精度直接积分的数值求解方法*

张 萍 刘 宁 聂鑫鹏 吉增强

(1.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学) 天津 300130；2.河北工业大学人工智能与数据科学学院 天津 300130；3.中电建(海口)新能源有限公司 海口 570100；4.河北燃气有限公司 石家庄 050000)

1 引言

单/多导体传输线的数学模型—传输线方程，作为一阶双曲型偏微分方程组，并没有固定的求解方式，利用现有的数学手段并不能得到其精确的解析解[1-2]，但是可以利用数值计算方式，得到其较为准确的数值解。

用于求解传输线方程的数值方法分为两类：频域法和时域法。对于频域分析方法，就是利用拉普拉斯变换将传输线方程转化为纯代数方程，在频域内求得电压、电流的频率响应，再通过拉氏反变换得到其时域解[3-4]。

对于大规模集成电路电压、电流的计算，频域分析法存在计算量较大的问题。因此一般考虑在时域内求解传输线方程。比较常用的时域分析方法有时域有限差分法、Lax 差分法、Upwind 差分法和Lax-Wendroff 差分法等。上述方法均需要利用一定的离散方法将传输线方程转换成一阶拟线性偏微分方程组，然后进行计算，其推导过程较为复杂，并且在计算过程中涉及到大量状态矩阵求逆运算，数值计算精度以及计算效率较低，并且对离散的时间步长和空间步长有一定的稳定性要求[5-7]。

为解决传统数值运算中出现的推导过程复杂、大量的状态矩阵求逆运算以及计算时间、空间步长影响数值稳定性等问题，本文提出利用求解一阶线性常微分方程组的数值方法对单/多传输线的数学模型-传输线方程进行数值分析[8]。求解过程主要有两个步骤：一是将传输线方程利用紧致有限差分法进行空间四阶离散，将得到的状态方程组利用矩阵转换得到一阶线性常微分方程组[9]；二是利用精细积分法与微分求积法(Differential quadrature method,DQM)相结合的高精度单步积分法对一阶线性常微分方程组进行求解[10-11]。通过理论分析可以得出，本文算法有固定的计算格式，且没有涉及到状态矩阵的求逆运算，其稳定性和计算时间步长无关等优势，可提高计算精度以及计算效率，最后通过仿真实例验证本文算法的优越性。

2 高精度单步积分法

针对一阶常系数微分方程的初值问题[12]

式中，t、tf分别为时间变量和截止时间；f(t,X(t))为时间变量t对状态变量X的函数；X0为状态变量X在初始时间t0的函数值。

经过一系列的数值变换可将式(1)变成常系数微分方程形式

式中，H为n阶定常数矩阵；r(X,t)为关于X、t的非线性函数。

在一个时间积分区间[tk,tk+1]，运用矩阵指数函数和卷积运算可得到式(3)精确的时域动态响应[13]。

式中，τ为时间积分区间[tk,tk+1]内任意时刻；Xk为时间tk时刻函数值，为给定值。Xk+1为tk+1时刻函数值，为待求值。

将式(3)等号右边第一项用精细积分法计算[10]，可得Xk+1计算公式为

其中，T=exp[(tk+1－tk)H]=exp(ΔtH)可用精细积分法求得，等式右边第一项计算精度可以达到计算机精度，故数值误差主要来源于等式右边的第二项积分，此积分又被称为Duhamel 积分。本文采用时域微分求积法对Duhamel 积分项进行近似求解。

2.1 Duhamel 积分项计算格式

对于式(1)中一阶常微分方程的初值问题，s阶时域微分求积法可以表示为[11]

式中，Δt是积分时间步长；cj是网格点；mij和nj是与网格点相关的积分系数[14]。

故式(4)中Duhamel 积分项的计算公式可写为

式中，i=1,2,…,s；t i=t k+i×Δt/s。

对于式(6)中的Xˆk+i/s，采用4 阶Runge-Kutta进行预估，此时s=4，故i=1,2,3,4。Xˆk+i/s计算公式为[15]

式中，

根据指数矩阵乘法可得以下关系式

再次利用精细单步求积法计算指数矩阵T3=exp(HΔt/4)，然后利用式(9)的方法求得T1、T2。当求出Duhamel 积分项的近似值后，将其代入式(4)得到Xk+1。

尤为注意的是，上述算法不涉及到矩阵的求逆，不会因多次求逆而导致数值误差，并且对于线性常微分方程组，式(7)的预估过程可以省略，因此在很大程度上提高了计算效率。

2.2 算法稳定性分析

根据傅里叶方法可得迭代公式的稳定性条件，故本文方法稳定性条件为[16-17]

从式(10)可知只要Re( Δt⋅λi) ≤ 0即能满足算法的稳定性要求。其中λi为矩阵H的特征值；Δt为计算时间步长，是正实数。所以本文算法稳定只需要Re(λi) ≤ 0，即时间步长Δt的取值并不影响算法的稳定性。

3 电报方程空间离散格式

描述传输线的电报方程时域形式为[18]

式中，L0、G0、C0、R0分别为变压器绕组的单位长度电感、电导、电容、电阻参数；t为时间变量；x为空间变量；u(x,t)、i(x,t)为传输线上关于空间、时间的电压和电流列矢量。

为了获得线路沿线的电压和电流变量，将整条传输线均匀分成N段。假设传输线长度为L，则每段长度Δx=L/N，设un为x=n⋅Δx处的电压值，n∈处的电流值，n∈[1,N]，如图1 所示。

图1 传输线分段模型

本文采用紧致有限差分法(Compact finite difference, CFD)对电报方程进行离散，基于CFD 的空间四阶差分公式为

式中，Y(x)为u(x)或i(x)，k1= 1/24，k2= 1 -2k1。

电报方程的空间四阶离散格式为

对传输线的首尾端采用空间二阶插值公式

传输线首尾的离散格式为

式中，0i、ni分别为首端和尾端电流。

根据式(13)、(15)、(16)可得2N+1 个状态方程，故可得其矩阵形式的线性常微分方程组

式中，H1、H2、s(t) 参数分别为

矩阵H1、H2中的参数分别为

将式(17)转化为以下标准形式

式中，r(t) 为离散后的源项；，H为常数矩阵，H=-H1-1，r(t) =H1-1s(t)。

以上推导没有结合实际线路的边界条件，下文将给出具体线路的边界条件。

4 仿真算例

4.1 单导体传输线模型

如图2 所示，单相高压长输电线路系统在t=0.0 s 时断路器接通，实际输电线路空载，在空载线路首尾两端分别连接电阻Rs和RL，电阻值为10 Ω。空载输电线路长度为l，假设输电线路为均匀线路，其参数R0、L0、C0分别为输电线路单位长度的电阻、电感和电容值。为了计算空载输电线路的末端电压uN，采用传输线方程对输电线路系统进行建模。

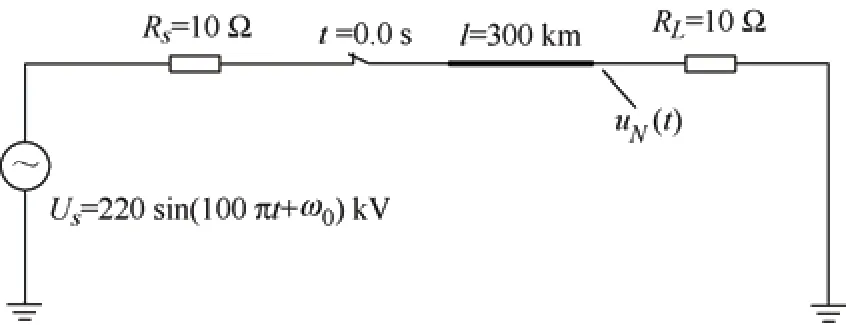
图2 单相高压长输电线路系统示意图

当进行合闸操作时，线路系统两端满足以下条件

将整个线路平均分成30 段，即N= 30。系统输入正弦电压信号US，其初始相位ω0= π/2。

采用本文方法对上面空载线路的末端电压uN进行计算，计算时间步长为Δt，并在不同的时间步长内与时域有限差分法(Finite difference time domain，FDTD)结果做对比，具体仿真结果如图3～6 所示。

图3 空载线路末端电压uN 仿真结果(Δt=1 μs)

图4 空载线路末端电压uN 仿真结果(Δt=40 μs)

图5 本文方法在不同时间步长下空载线路末端电压uN 仿真结果

图6 两种方法在不同时间步长下空载线路末端电压uN仿真结果(本文方法Δt=40 μs，FDTD Δt=1 μs)

由图3～6 仿真结果可得如下结论：① 本文方法所得结果与FDTD 所得结果基本一致，可验证本文方法的有效性；② 无论使用本文方法还是FDTD计算线路的末端电压，都会产生一定的数值振荡。不同的是，本文所用方法产生数值振荡较小，计算精度较高；③ 本文方法使用于FDTD 的40 倍仿真时间步长时，本文所用方法的仿真结果基本没有变化，但是采用FDTD 得出的计算结果，其振荡会加剧，验证了本文算法的稳定性并没有受到仿真步长的影响，以及可利用大步长进行仿真计算，提高计算效率。

4.2 多导体传输线模型

为扩展本文算法适用性，将本文算法用于实际大型变压器绕组暂态过电压的计算。

特快速暂态过电压(Very fast transient overvoltage，VFTO)进入大型电力变压器会对其绕组产生绝缘损坏，因此计算在VFTO 下大型电力变压器绕组的匝间过电压能有效预防绕组的绝缘损坏。

在不考虑变压器组件频变效应情况下，将变压器绕组等效成一根根首尾相连的传输线，如图7 所示，故可用描述多导体传输线的电报方程进行建模研究[19-20]。

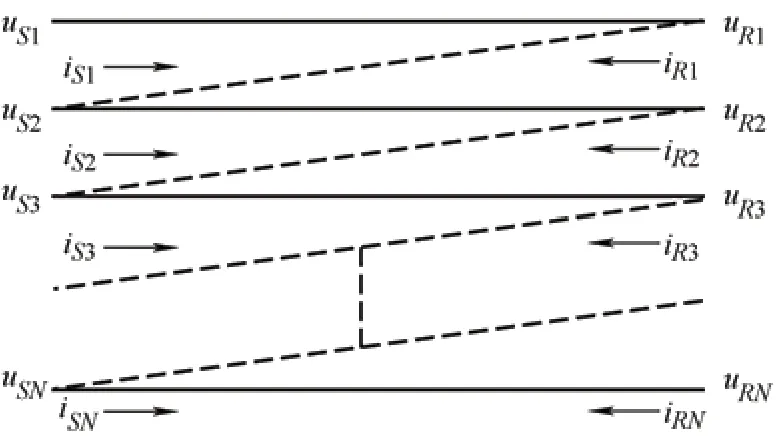
图7 变压器绕组的多导体传输线模型

图7 中，uS和uR表示每匝绕组的输入端电压与输出端电压；iS和iR表示每匝绕组的输入端电流与输出端电流。

大型电力变压器绕组的多导体传输线模型对应的电报方程中R0、L0、C0、G0分别是单位长度的电阻、电感、电容、电导矩阵。变压器模型及其基本参数如表1 所示。

本文所用大型电力变压器模型是由保定天威集团提供的江西丰城SFP-800000/500 自耦变压器，双线圈高低高结构，自铁心向外绕组排列：内高压(Hi)、低压和外高压(Ho)；单相接线方式为YNd11 三相牵引；其铁心形式为单相三柱式结构，如图8 所示。其中A到X1 为外高压绕组，采用内屏蔽连续式，上下对称，具体线段数及段内匝数如表1 所示。A1到X为内高压绕组，分为4 饼，每饼匝。

变压器绕组首端接入50 Ω 电阻，即RS=50 Ω，尾端接地。可得绕组的边界条件为

式中，e0为冲击电压源。

冲击电压源e0为上升时间4 ns，峰值639 kV的冲击电压源，如图9 所示。利用本文方法与FDTD计算在同一变压器模型下A 段8 匝绕组的末端过电压，如图10～12 所示。

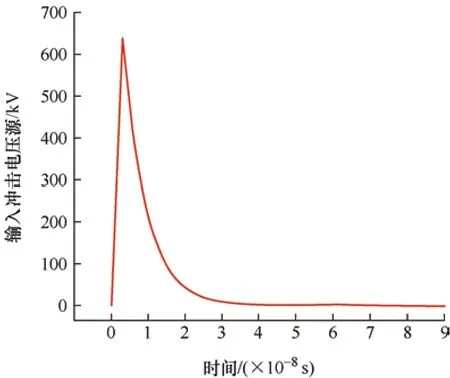
图9 冲击电压源

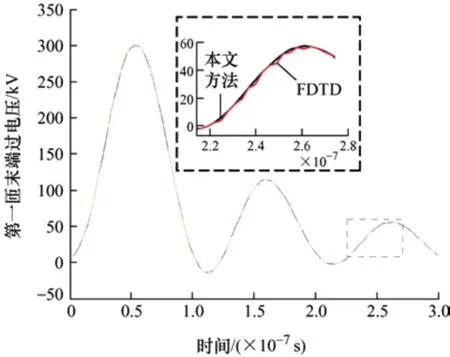
图10 第1 匝末端过电压

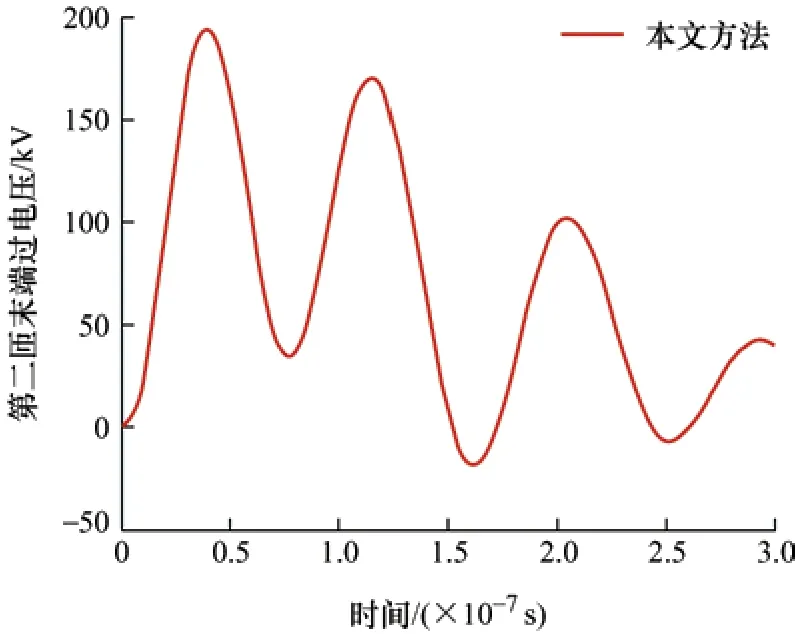
图11 第2 匝末端过电压

图12 前8 匝末端过电压

由图10～12 仿真结果可得如下结论。

(1) 本文方法仿真波形与FDTD 仿真波形基本一致，可验证本文算法在大型电力变压器绕组电磁暂态计算模型的实用性。然而由于计算过程中出现大量的矩阵求逆运算，影响了数值计算精度，FDTD仿真结果局部出现了较为轻微的数值振荡。

(2) 从大型变压器绕组自身分析：① 前几匝绕组的末端过电压的最大值出现在第一匝末端，为冲击电压源幅值的47%；② 随着匝数的增加，绕组末端过电压幅值在不断减小。并且在每一匝仿真时间内，电压值随着时间的增加而逐渐衰减。

5 结论

本文提出结合精细积分法与时域微分求积法对传输线方程进行求解。通过对算法的推导以及仿真实例验证，可得出以下结论。

(1) 由算法稳定性条件可知，本文方法稳定性条件与时间步长无关。FDTD 的计算时间步长则要满足稳定条件：Δt≤Δx/c(c=3×108m/s)，因此本文算法可利用大步长进行仿真计算，提高计算效率。

(2) 本文方法避免了因状态矩阵求逆而带来的数值误差，抑制了数值振荡，提高了计算精度。

(3) 首次将本文方法用于计算VFTO 下大型电力变压器绕组的过电压，由仿真结果可知，变压器第一匝绕组中VFTO 的幅值最大，并随着匝数的增加，VFTO 的幅值呈递减状态，在实际工程中，应注重变压器绕组首端的绝缘保护。