倾斜状态下受电弓滑板温度特性仿真研究*

曾佳帅 刘桂芬 王智勇 王 琦

(辽宁工程技术大学电气与控制工程学院 葫芦岛 125105)

1 引言

在高速电气化铁路系统中，弓网系统是列车受流的重要部件，是保障列车系统正常运作的关键。在实际情况下，由于工人安装不当，大风大雪等恶劣天气，以及接触导线悬挂不良等因素的影响，接触线与滑板之间容易产生轻微偏角，铜导线难以和滑板保持完全平滑状态，以至于产生高温聚集的情况，对滑板造成损伤。因此，对倾斜运行状态下受电弓滑板的温度特性进行系统研究，对延长滑板使用寿命有着积极意义。

针对弓网系统摩擦副的温度特性，国内外学者进行了一系列研究。文献[1]利用COMSOL 软件建立了弓网系统摩擦副温度场仿真模型，对高速、强电流条件下的电弧能量进行预测；文献[2-6]对滑动电接触下的热模型进行了研究，对不同工况下的电接触进行了热分析；文献[7]建立了弓网系统的电触点热模型，构建了接触点之间的最大接触加热和加热分布表达式；文献[8-10]从多方面考虑，提出和完善了弓网系统的建模方法；文献[11]在温度场仿真分析中提出一种变密度对称六面体网格划分方法；文献[12]设计了一套基于LabVIEW 的弓网检测系统；文献[13]采用欧拉-伯努利柔性梁对柔性承力索和接触网进行建模，对弓网耦合系统进行了整体分析；文献[14]基于自制的弓网仿真系统，从温升方面研究了弓网系统电接触的演变过程。国内外大量学者对正常状态下弓网系统温度场进行研究，关于倾斜状态下弓网系统温度场的研究较少，只有文献[15]对不同倾角下滑板的磨损量、摩擦因数以及电弧能量进行分析，关于倾角状态下的滑板温升仿真还鲜见报道。

本文利用滑动电接触试验系统进行滑板倾斜条件下的温度特性试验，在COMSOL Multiphysics 软件中运用等效面积法模拟滑板倾斜，建立了倾斜状态下弓网系统滑动电接触温度场仿真模型，仿真与试验相同工况下的温度结果，通过对比仿真与试验结果验证了仿真模型的准确性；对高速强电流状态下的滑板温度结果进行仿真计算，分析了倾角对滑板温度及其温度分布的影响。

2 试验装置与方案

2.1 试验装置及原理

如图1 所示，滑动电接触试验系统由电波暗室、弓网电弧发生器和弓网电弧检测装置组成[1]。该装置能模拟电力机车弓网系统的“之”字型运动，同时对接触压力、滑动速度、接触电流值等进行调节。试验中利用FLIR-T400 型红外热像仪对滑板温度进行采集，利用LabVIEW 对滑板两侧的电压以及线路电流波形进行采集。倾斜试验铜导线转盘与浸金属滑板间摩擦副结构图如图2 所示。

图1 弓网滑动电接触试验机

图2 倾斜状态下滑板的安装结构示意图

2.2 试验方案

为了研究不同工况下，不同倾角对滑板温度的影响，试验方案如表1 所示。试验共进行30 组，分别研究纯摩擦情况下与70 A 电流情况下滑板的稳态温升情况。

表1 试验方案

3 仿真模型

3.1 模型建立

在文献[16]建立的弓网系统滑动电接触的模型之上进一步考虑滑板倾斜角度因素对滑板温升的影响，利用COMSOL Multiphysics 软件进行仿真计算。

利用COMSOL 软件对弓网系统试验机进行等尺寸建模。应用固体力学、固体传热及电流物理场设定边界条件。如图3 所示为仿真模型图，图3 中圆环为弓网系统旋转铜导线，在X-Y平面以Z轴为轴心做圆周运动；两个六面体为浸金属碳板，在X轴方向上做往返运动以模拟弓网系统“之”字形运动。

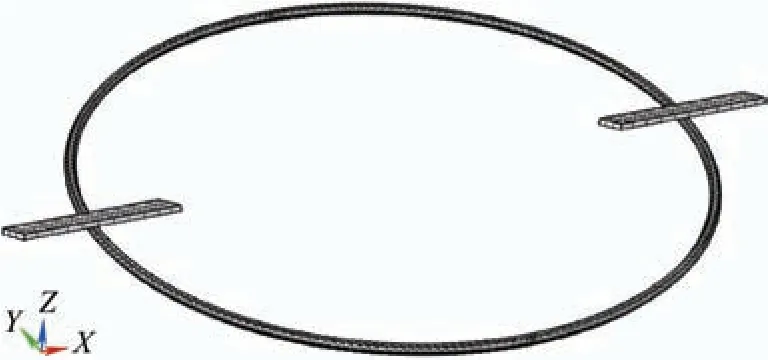
图3 仿真模型图

为使仿真便于计算，做出以下假设[16]：① 材料密度与导热系数为定值，不随温度变化而改变；② 考虑外界产生的对流散热，散热系数恒定；③ 忽略磨屑带走的很少热量；④ 接触点界面摩擦力作用转换的热量和接触电阻产生的热量能全部被摩擦耦合件吸收；⑤ 各层材料的参数都是各向同性的。

仿真设定初始温度为实际室温15 ℃，本模型中浸金属滑板以及铜导线的物理参数参考文献[1]中设置。

3.2 等效面积法模拟滑板倾斜

试验初始状态，由于设定了一定倾角，摩擦副滑板与铜导线接触面积极小；试验进行中，试验机模拟列车“之”字形运动，铜导线与浸金属滑板相互摩擦，滑板接触面不断磨损导致摩擦副接触面不断增大，从而使得铜线在滑板上滑动区域面积增加。COMSOL 软件中难以模拟滑板的倾角以及试验过程中滑板磨损导致的滑动区域变化状态，于是采用等效面积法模拟铜线在滑板上滑动区域不断增大的过程。等效面积法即通过试验采样得到的滑动区域面积来设置COMSOL 中滑板周期运动的函数幅值，使得相同时间内铜线在滑板上滑动的区域与试验相等。

试验过程每隔100 s 对滑板摩擦区域拍照取样，利用Matlab 对图片摩擦区域与非摩擦区域进行二值化处理。如图4a 所示为无倾角长时间磨损后的浸金属滑板采样照片，图4b 为二值化后的滑板图片，其中白色区域为铜导线在滑板上的滑动摩擦区域，黑色区域为未受到摩擦的区域；已知采样总面积大小，计算摩擦区域像素点个数以及占总区域像素点个数的比例大小以计算滑动区域面积。

图4 滑板摩擦区域图像处理

将试验过程中滑动区域面积采样数据转化成仿真模型中滑板往返运动的幅值，对其进行三次样条插值计算，得到滑板运动幅值随时间变化的函数曲线，如图5 所示；将运动幅值与滑板运动频率结合，得到滑板位移随时间变化曲线，图6 是倾角为2°的滑板运动曲线，滑板倾斜状态下滑动过程即转化成如图6 所示的滑板运动幅值不断增大的往返运动；初始时刻放大图如图7 所示。

图5 不同倾角下滑板运动幅值

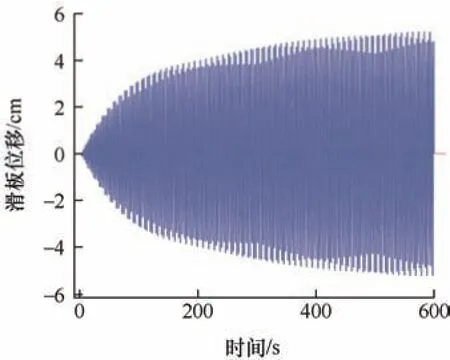
图6 滑板位移曲线图

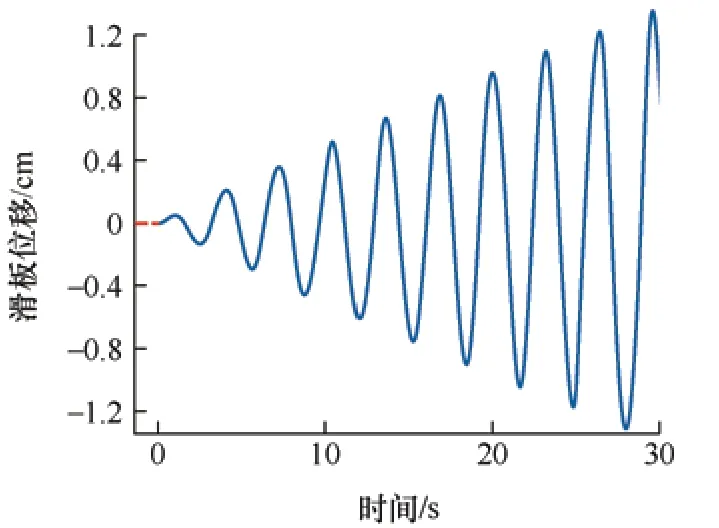
图7 初始时刻放大图

速度、接触压力、温度和接触电阻VIP 数值较小，对浸金属碳板磨损量解释能力较弱[17]；大电流对浸金属碳板磨损的影响主要体现在电弧对滑板的烧蚀作用[18]，电弧对滑板的烧蚀呈现细小麻坑状，麻点对接触面积的影响微小，且倾斜状态下的接触面积比正常状态时的小很多，因此接触面麻点数量也相对少很多。此外，仿真难以准确模拟电弧对滑板的烧蚀作用，并且倾斜状态下的滑板温度上升到稳定温度所需的时间较短，因此仿真只考虑倾角大小对滑动区域面积的影响。

3.3 弓网电弧能量计算预测

滑板温升热量来源主要是摩擦热、焦耳热和电弧热[2]。如图8 所示为倾角1°，滑动速度90 km/h，接触电流70 A 条件下滑板两端电压波形图截取片段，滑板倾斜状态下由于铜导线与碳板接触面积较小，导致电弧的频繁产生，产生电弧时接触电阻值迅速增大使得电压突增，导致图8 所示“突刺”状电压波形，为了精确分析滑板温升情况，本文考虑了电弧对滑板温度的影响。

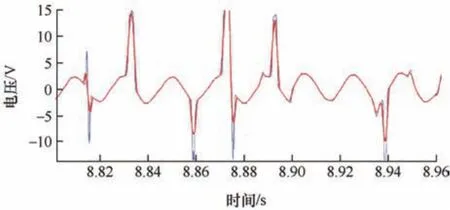
图8 滑板两侧电压波形图

利用试验过程中采集的电压电流数据对不同条件下电弧总能量进行计算。交流电弧能量为[19]

式中，hW为电弧能量；tx和ts分别代表燃弧和电弧熄灭的时间；uh为电弧电压；ih为电弧电流。

对各个倾角不同速度下的电弧能量进行计算，不同速度下电弧能量值相差最大2 502 J，相差占比3.2%，速度对电弧能量值影响较小。因此，仿真只考虑倾角与接触电流对电弧功率的影响。不同倾角下每100 s 内的电弧能量计算结果如表2所示，前100 s 内滑板与铜导线接触面积小导致大量电弧产生，随着滑板的磨损，接触面积不断增大，电弧逐渐减少，导致了如表2 所示的电弧能量随时间迅速降低直到小范围波动的状况。由式(1)可知电弧能量与电流值成线性关系，在Matlab 软件中采用一元线性回归模型对大电流条件下的电弧能量进行预测，求得倾角1°、2°、3°、4°在电流1 000 A 时600 s 内电弧总能量分别 为 9.45×105J、1.62×106J、1.29×106J、1.78×106J，按照表2 中不同时间段内电弧能量的比例得出不同倾角下每100 s 内电弧能量，从而得到每100 s 内平均电弧功率，在滑板接触面设置相同功率的点热源以模拟电弧热对接触面温度的影响。

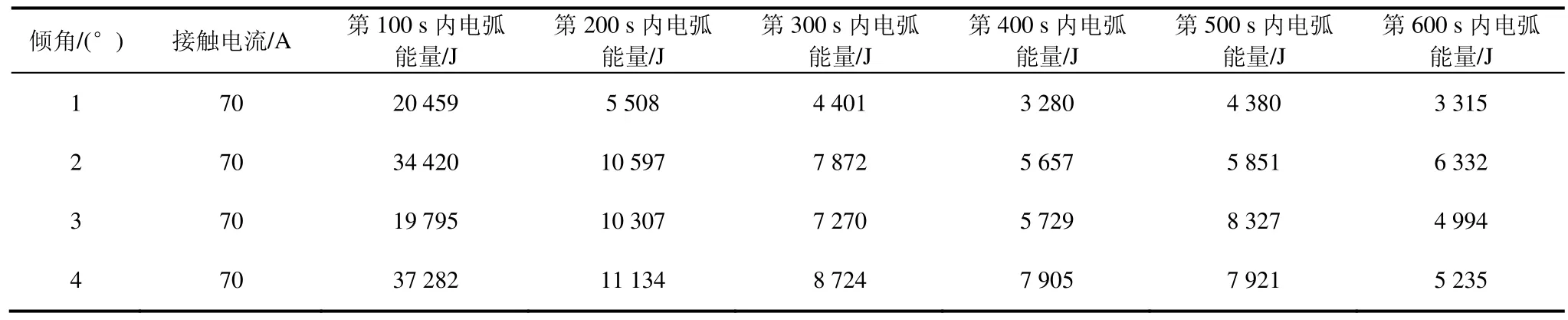
表2 电弧能量计算

4 仿真模型验证

4.1 瞬态温升对比验证

使用热成像仪间隔100 s 对滑板接触面最高温度进行采集，采样数据与仿真温升曲线对比验证仿真模型的准确性。在速度为70 km/h、接触压力为70 N 条件下进行仿真计算。

图9 为倾角1°、接触电流70 A 条件下仿真试验结果对比图，图10 为无电流纯摩擦倾角为2°条件下仿真试验结果对比图。两者最大误差分别为4.6 ℃和2.9 ℃，试验采样数据与仿真温升曲线基本拟合，可以验证仿真分析的准确性。

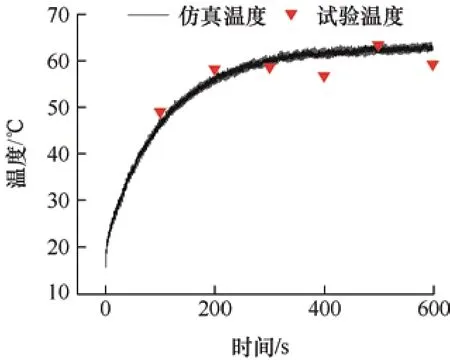
图9 70 A 瞬态温度验证

4.2 稳态温升对比验证

改变试验的倾角与速度大小，分别对纯摩擦和有电流作用下两种情况试验仿真结果进行对比。

如图11 所示为电流70 A 条件下试验仿真温度结果对比，如图12 所示为纯摩擦0 A 条件下温度对比。仿真试验结果对比发现，70 A 电流情况下温度误差最大为3.5 ℃；0 A 纯摩擦情况下温度误差最大为1.9 ℃。误差在允许范围内，证明仿真模型有效。

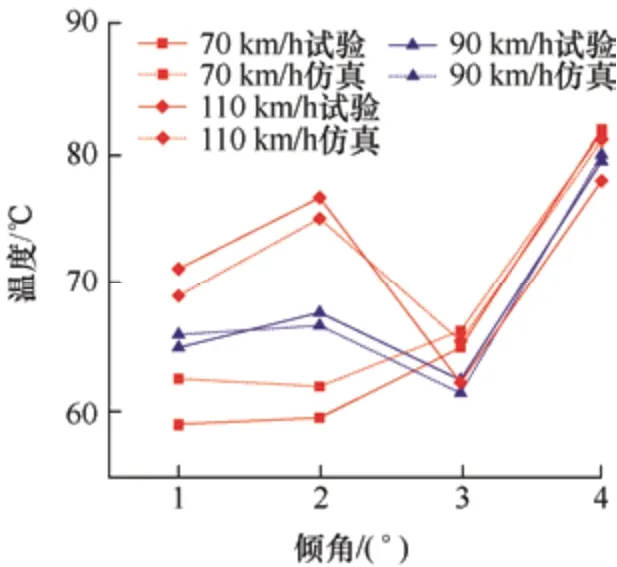
图11 70 A 电流仿真试验温度对比

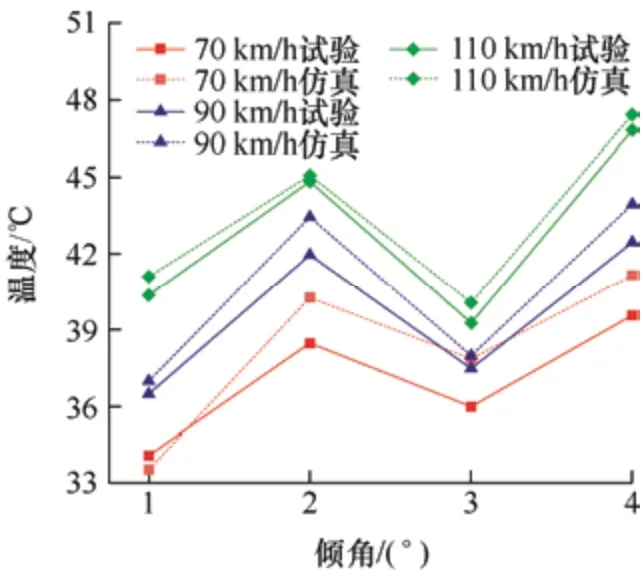
图12 0 A 电流试验仿真结果对比

5 温度特性仿真

5.1 不同倾角状态下温度仿真

5.1.1 高速大电流温度仿真

对真实的列车运行条件进行不同倾角的温度仿真，取接触压力为70 N，对不同倾角下接触电流和滑动速度分别为1 000 A、380 km/h；1 000 A、160 km/h；500 A、160 km/h 条件下进行温度仿真。如图13 所示为各组稳态温度仿真结果。

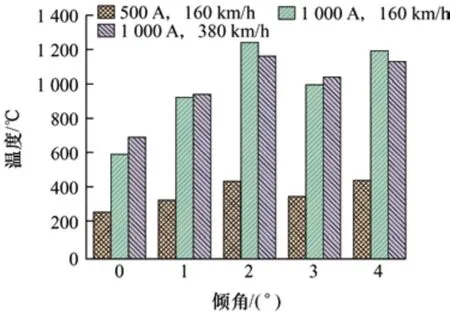
图13 大电流高速温度仿真结果

从图13 可以看出在各组试验中，正常状态下各组条件下温度结果都远小于倾角状态下的温度，其中接触电流1 000 A、滑动速度160 km/h 条件下，倾角2°相比正常状态高了643 ℃，温度相差巨大，可见倾角对滑板温度的影响显著。不同倾角温度差距主要体现在大电流情况下，在大电流条件下稳态温升对速度的敏感度较低，速度的变化对稳态温度影响较小，而在倾角为2°与4°时与其他情况不同，速度的增大引起温度的下降；且电流的增大引起稳态温度剧烈变化。

分析认为倾角状态下温度相比正常状态明显增大是由于倾角状态下的大量电弧热的影响，且滑动区域相比正常状态较小，产生的焦耳热与摩擦热在小范围内聚集难以扩散，两者同时造成了滑板接触面温度的大量提升；从表2 中电弧能量数据看出，倾角2°、4°时电弧能量相比于其他倾角大了很多，电弧热在接触面聚集更多，且仿真考虑了铜线转动带动的空气流动，2°、4°热量相比其他倾角聚集更多，则受到空气流动散热越多，当热量的扩散速度大于摩擦热的增加，则导致了图13 中2°、4°倾角速度的增大引起稳态温度降低的现象；而电流的增大直接导致了焦耳热的剧增从而引起稳态温度的剧烈变化。

可见，在列车高速大电流条件下，倾角是受电弓滑板温度异常升高的最主要因素。

5.1.2 瞬态温升曲线仿真

为了探寻不同倾角状态下滑板温度从初始到稳态变化规律，在电流为1 000 A，接触压力为70 N，速度为160 km/h条件下对比了不同倾角状态时滑板表面中点上升曲线，如图14 所示。

图14 不同倾角时接触面中点温升曲线图

由图14 可以看出温升曲线呈波动状，短时间内温度有较大范围内波动；无倾角状态上升曲线平缓，温升相比于倾角状态较小，在100 s 后上升到稳态后一直保持稳定状态；而倾角状态下采样点温度在50 s 内急剧上升至峰值，且在100 s 后温度有较大幅度的下降，呈现一种“山脊”状分布，在200～600 s温度也保持较小范围的起伏，整体有轻微下降趋势；2°、4°倾角相比于其他倾角有着更明显的“山脊”分布，其“山峰”更高，凸起更明显，前50 s 内温度上升更剧烈。

短时间内温度变化较大原因在于热源的移动，铜导线与滑板接触区域通过大量电流且产生电弧，导致接触区域温度迅速上升，铜导线在滑板上往返滑动，热源经过测量点时温度短暂上升，离开时温度降低，导致波动状曲线；前百秒内铜导线与滑板接触面积小，运行过程产生剧烈电弧，在大量电弧热与焦耳热、摩擦热的共同作用下导致其温度剧烈上升，百秒后随着滑板磨损，接触线面积增加，抑制电弧的产生，电弧总能量迅速减少，使之前的温度短暂稳态状态被破坏，温度随着电弧能量减少迅速降低，从图5 可以看出，滑板运动幅值在前百秒内增长最快，即滑动区域面积在前百秒增长最快，所以试验前期电弧能量下降更多，而随着不断磨损，接触面积增大得越来越慢，而使得电弧能量在小范围内下降，所以温升曲线后端会缓慢降低；而2°、4°的“山脊”状分布更明显，原因在于其前百秒内更大的电弧能量所导致。

可见，倾角不仅会大幅度提高滑板的稳态温度，在倾角刚产生的50 s 内，滑板的温度会急剧突增，远大于最终的稳态温度；温度的剧增可能会使浸金属滑板中的金属成分熔化，从而影响滑板的材料性能，进而影响到弓网滑动摩擦副的载流摩擦磨损特性，严重时甚至会威胁列车的安全运行。

5.1.3 不同接触压力下的稳态温度仿真

在电流为1 000 A，速度为160 km/h 的条件下，对不同倾角与接触压力下的稳态温度进行仿真，结果如图15 所示。

图15 不同倾角与接触压力下的温度仿真结果

文献[20]发现在电流速度一定的条件下，接触面温度随压力的增大呈现一种先减小后增大的“U”形趋势，即存在一个使接触面温度最低的最佳接触压力。

从图15 可以看出，在无倾角状态时，最佳压力值在70 N 附近；随着倾角不断增大，线段的最低点不断右移，到倾角2°时最佳压力点已经增大到75 N，倾角3°则在80 N 附近，倾角4°曲线一直向下倾斜说明最佳压力大于90 N；即最佳压力值随着倾角的增大往70 N 右侧移动，使得接触面温度最低的最佳接触压力随着倾角的增大而增大。分析其原因，在接触压力较小时接触斑点少，接触斑点的接触面积小，接触电阻大导致焦耳热多，而摩擦热较小，随着压力增大，接触电阻减小，焦耳热降低而摩擦热增大导致U 形分布；而倾角角度越大，接触面积相对于无倾角状态越小，导致接触电阻越大，即倾角状态要与正常状态保持相同的接触电阻需要更大的接触压力，因此导致了倾角状态的最佳接触压力右移。

在弓网系统运行期间，滑板倾斜会使滑动摩擦副的最佳接触压力发生变化，这不仅会影响滑板的稳态运行温度，还会引起滑板的异常磨损、影响列车的受流质量。

5.2 滑板温度分布

选取一组仿真试验观察滑板温度分布情况，在速度为160 km/h，压力为70 N，电流为1 000 A，倾角为4°的条件下，绘制稳态滑板温度分布，如图16 所示。

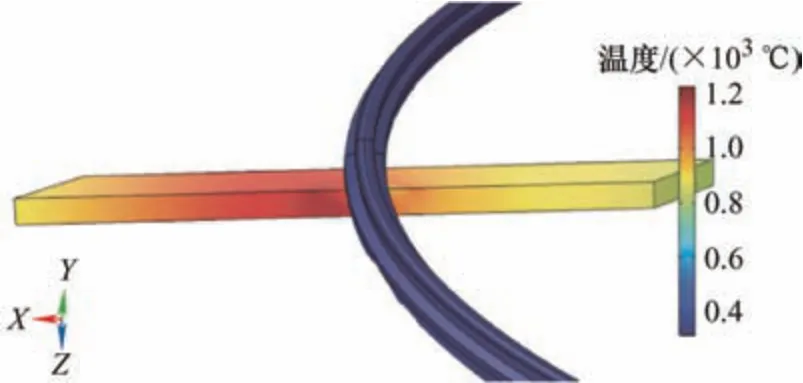
图16 滑板温度分布

从图16 可以看出，滑板温度主要聚集在滑板中央接触线上，温度分布由接触线向两侧均匀扩散降低，取滑板接触面X轴方向线段和过接触面中心点Z轴正半轴方向线段为截线，如图17 上半部分中线为X轴方向截线，下半部分中线为Z轴方向截线，分别取X轴方向截线最左端和接触面中点为温度零点，在速度为160 km/h、压力为70 N、电流为1 000 A仿真条件下，绘制不同倾角在截线上的温升分布情况，结果如图18、图19 所示。

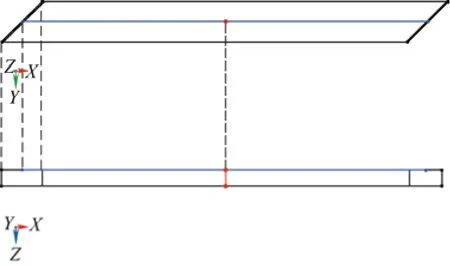
图17 截线位置示意图

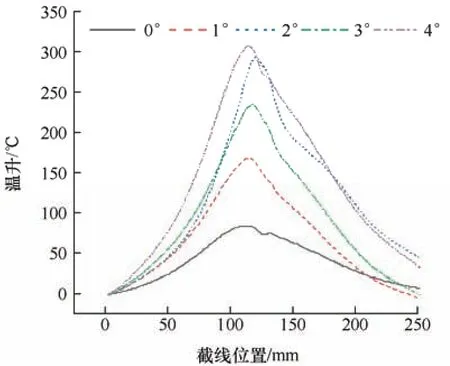
图18 X 轴方向截线上温升分布

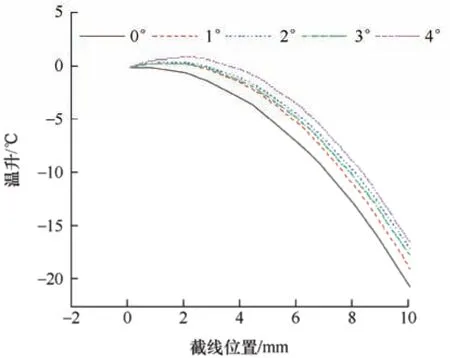
图19 Z 轴方向截线上温升分布

如图18 所示，从上到下分别为4°、2°、3°、1°、0°的X轴方向截线上温升曲线，可以看出滑板接触面X轴方向左右温度分布正常状态相比于倾角状态分布更均衡，而倾角状态的温度滑动接触区域相比两旁温度差异较大，温度集中在滑板中央部分；不同倾角条件下滑板倾角越大，电弧能量越高的滑板温升分布曲线越陡峭，峰状凸起越高，温度聚集程度越大；而图19 中从上到下分别为4°、2°、3°、1°、0°的Z轴方向截线上温升曲线，不同倾角下的滑板内部与表面温度分布均匀，温升差距不大。

分析上述滑板温度分布的原因是电弧热、摩擦热与焦耳热共同作用的结果。倾斜状态下产生剧烈电弧且都集中在小范围接触区域内，高温聚集区域是电流密度模最密集的区域，并且是最主要接受摩擦的区域。此外，模拟倾角状态导致滑板左右运动幅值较小，铜线与滑板一直在小范围内相对摩擦，这些因素是高温聚集在小范围内的主要原因。倾角越大，滑板运动幅值越小，且伴随着更高的电弧能量，温度分布越聚集。

从上述滑板温度分布情况来看，正常状态时滑板的温度分布会更加均匀，倾斜状态时滑板中部的温度比两侧的温度提升得更高，滑板的高温区主要聚集在接触表面中心附近的较小区域内，高温区的聚集会影响滑板的散热，改变滑板的热、力、机械性能，最终会缩短滑板的使用寿命。

6 结论

本文利用COMSOL 软件建立倾斜状态下的弓网系统温度场仿真模型，对倾斜状态下受电弓滑板的热电特性进行仿真研究。

(1) 仿真考虑了电弧热的作用，采用等效面积法模拟倾斜状态，利用试验结果从瞬态和稳态两方面验证了仿真模型的准确性。

(2) 通过控制变量法对不同倾角时大电流高速状态下滑板的温度特性进行了仿真计算，发现倾角是滑板温度异常升高的最主要因素。

(3) 大电流条件下滑板的温度对滑动速度的敏感度较低；滑板温升曲线呈“山脊”状分布，倾角状态初期滑板温度急剧增大，容易达到滑板内金属成分的熔点，对滑板结构造成影响。

(4) 最佳接触压力随着倾角角度的增大而增大，导致滑板异常磨损，影响滑板使用寿命。倾角状态下滑板的高温区域聚集在滑板接触表面的中央，高温聚集会缩短滑板的使用寿命。

不足之处在于大电流下滑板表面的温度可高达上千摄氏度，温度变化范围较宽，可能会影响到滑板材料的物理特性。本文在仿真计算时，暂未考虑温度大范围变化对滑板物理特性参数的影响，这可能对结果有一定影响；其次使用电流线密度来刻画倾斜可能使得仿真结果更加精确，受限于试验器材等难以实现。滑板倾斜状态下不管是温升或是温度分布情况都不利于弓网系统的正常运行，避免滑板倾斜对列车的安全稳定运行以及延长滑板的使用寿命有着积极意义。