饱和地基水泥土复合桩近场主动隔振的BEM-FEM耦合分析

时 刚, 郜新军, 张 浩

(郑州大学 土木工程学院,郑州 450001)

进入二十一世纪,为缓解城市日益增长的交通压力,各大城市纷纷进行轨道交通和高架路建设。由于城市土地资源紧张,不可避免地在地铁沿线、城市主干道等周边进行建设。然而,地铁运行、汽车行驶会产生环境振动污染,对邻近居民的日常生活、精密仪器设备运行等产生负面影响,严重时还会危及老旧建筑的安全。国际已把振动污染列为“七大环境公害”之一。因此,对各种人工振动污染的治理成为当前急需解决的重要课题之一,在地基中设置隔振屏障是振动污染治理的一种有效方法[1]。实际工程中常用的隔振屏障有多种形式,例如连续屏障(空沟、填充沟等)和非连续屏障(排桩、排孔等)[2]。考虑到土体稳定性、工程造价等问题,空沟、填充沟等连续屏障深度一般设置较浅,难以对低频振动起到有效的隔振作用,此时排桩是一种更好的选择。

国内外众多学者对排桩隔振问题进行了大量的研究工作。在试验研究方面,Woods等[3]采用全息照像技术对桩列的隔振效果进行了研究;Liao等[4]采用水波比拟法进行了水中桩列隔振的模型试验;刘晶磊等[5-6]开展了单排桩、双排桩近场主动隔振的模型试验研究;姜广州等[7]则针对层状土中双排环形排列桩的隔振效果开展了试验研究。在理论研究方面,Aviles等[8-9]采用波函数展开法分别研究了SH波、SV波和P波入射时单排桩的隔振效果;Gao等采用积分方程法研究了排桩远场被动隔振问题;徐平等[10-11]采用波函数展开法分别研究了单排刚性桩和单排空心管桩对弹性波的隔振问题;夏唐代等[12-13]基于改进的多重散射方法研究了双排桩和多排桩对对弹性波的隔振效果;陆建飞等[14]、徐满清[15]分别采用虚拟桩法研究了饱和地基中排桩对移动荷载引起环境振动的隔振问题。在数值研究方面,Kattis等[16-17]采用三维边界元法(boundary element method,BEM)对桩列的隔振效果进行了计算分析;Tsai[18]等则研究了空心管桩对基础竖向振动的隔振效果;时刚等[19]采用半解析BEM研究了饱和地基中单排桩的远场被动隔振问题;Ai等[20]采用解析层单元法研究了单排桩在横观各向同性多层介质中的隔振效果;Alamo等[21]基于层状半空间Green函数建立了一种高效数值模型,研究了下卧基岩地层中排桩的隔振效果;Shan等[22]分别采用积分方程方法和有限元法(finite element method,FEM)研究了隔振排桩对区间隧道地铁行驶振动的隔振效果。

上述研究主要对单排桩或多排桩的隔振问题进行计算分析。近年来,部分学者基于声子晶体的带隙理论[23]提出了周期性排桩隔振方法,孟庆娟等[24]采用COMSOL软件分析了饱和土中周期性排桩的隔振性能;Huang等[25]研究了周期性排桩的减振带隙,并将其应用到平面波的隔振问题中;Pu等[26]基于Boit理论和Floquet-Bloch理论研究了饱和地基中周期性排桩对入射Rayleigh波的隔振问题。

然而在城市中进行隔振排桩施工时,钻孔灌注桩施工容易造成周边环境的泥浆污染问题,PHC管桩等预制桩施工会带来噪音、振动或挤土效应等负面影响。为解决传统桩基施工的环境影响问题,近年来出现了一种水泥土复合(stiffed deep cement mixing,SDCM)桩技术[27],具有低振动、低噪声、无挤土、少排泥浆等优点,是一种对环境影响小的新型桩基技术。众多学者和工程技术人员对水泥土复合桩进行了研究,但这些研究主要涉及新型基桩施工工艺研发、承载机理等方面的研究[28-30],目前尚未见该型基桩应用于屏障隔振的文献。

本文以城市中人工振动污染的治理为背景,采用水泥土复合桩技术构建排桩隔振体系,研究饱和地基条件下单排水泥土复合桩对动力机器基础诱发环境振动的近场主动隔振问题。采用饱和土半解析BEM对集中荷载作用下明置动力机器基础和饱和地基进行建模,采用FEM对水泥土复合桩进行建模,根据饱和地基-水泥土桩交界面上的平衡和相容条件,建立单排水泥土复合桩近场主动隔振的半解析BEM-FEM耦合方法,并对单排水泥土复合桩的近场主动隔振问题进行了计算分析和初步探讨。

1 明置动力机器基础振动的半解析BEM分析

图1 动力机器基础示意图

本文假定半空间为饱和地基的情况,根据文献[31],饱和地基上动力机器基础稳态振动的边界元方程可表示为

(1)

动力机器基础的振动通过基础-地基接触面向地基内部传递,在地基中产生弹性波。本文考虑饱和地基的情况,采用饱和土半解析BEM对地基进行建模。饱和地基振动的边界元方程可表示为

(2)

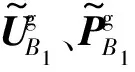
根据刚性基础-饱和地基接触面的平衡条件和相容条件,有：

(3)

式中,nB1为接触面上边界节点的法向量矩阵。

将式(3)代入式(2)和式(1),整理后可得饱和地基上明置动力机器基础振动影响的三维半解析BEM方程为

(4)

式中,0和I分别为零矩阵和单位矩阵。

求解式(4)即可得到刚性基础-饱和地基接触面上的未知量和刚性基础的位移向量,再根据式(1)和式(2)计算其他未知量。

由于采用半解析BEM,为获得饱和地基表面任意一点的振动,可采用“内点”的边界积分方程,计算各“内点”的位移和孔压

(5)

式中,x为饱和地基表面计算点的坐标向量。

2 水泥土复合桩近场主动隔振的半解析BEM-FEM耦合方法

动力机器基础振动会对周边环境造成振动污染,为减小振动污染,可在动力机器基础周边设置屏障进行隔振。

当采用水泥土复合桩进行屏障隔振时,若采用BEM对水泥土复合桩进行建模,除需要在水泥土桩外表面进行边界单元划分外,还需要在水泥土-芯桩交界面进行边界单元划分,大大增加了BEM前处理和BEM方程组组装的难度,计算量也随之增加。若采用FEM对水泥土复合桩进行建模,可充分发挥有限元方法在多域(多种材料域)问题建模中的优势,从而可大大降低水泥土复合桩隔振问题的建模难度。

本文主要研究饱和地基中单排水泥土复合桩对动力机器基础振动影响的近场主动隔振效果,饱和地基和动力机器基础振动仍采用饱和土半解析BEM进行建模,而水泥土复合桩采用FEM建模,通过饱和地基-水泥土桩接触面的相容条件和平衡条件将两部分模型耦合起来,这样就形成了饱和土半解析BEM-FEM耦合方法。

采用饱和土半解析BEM-FEM耦合方法分析单排水泥土复合桩近场主动隔振问题的示意图如图2所示。

2.1 饱和地基振动的半解析BEM方程

采用饱和土半解析BEM计算单排水泥土复合桩对动力机器基础振动影响时的隔振效果,除在动力机器基础-饱和地基接触面上进行边界单元划分外,还需要在饱和地基-水泥土桩接触面进行边界单元划分,见图2(b)。此时,饱和地基振动的BEM方程可表示为

(6)

式中：下标“Ba”表示饱和地基的全部边界元节点的量;“B2”表示饱和地基-水泥土桩接触面的边界元节点(后文也用于表示该部分边界)的量。

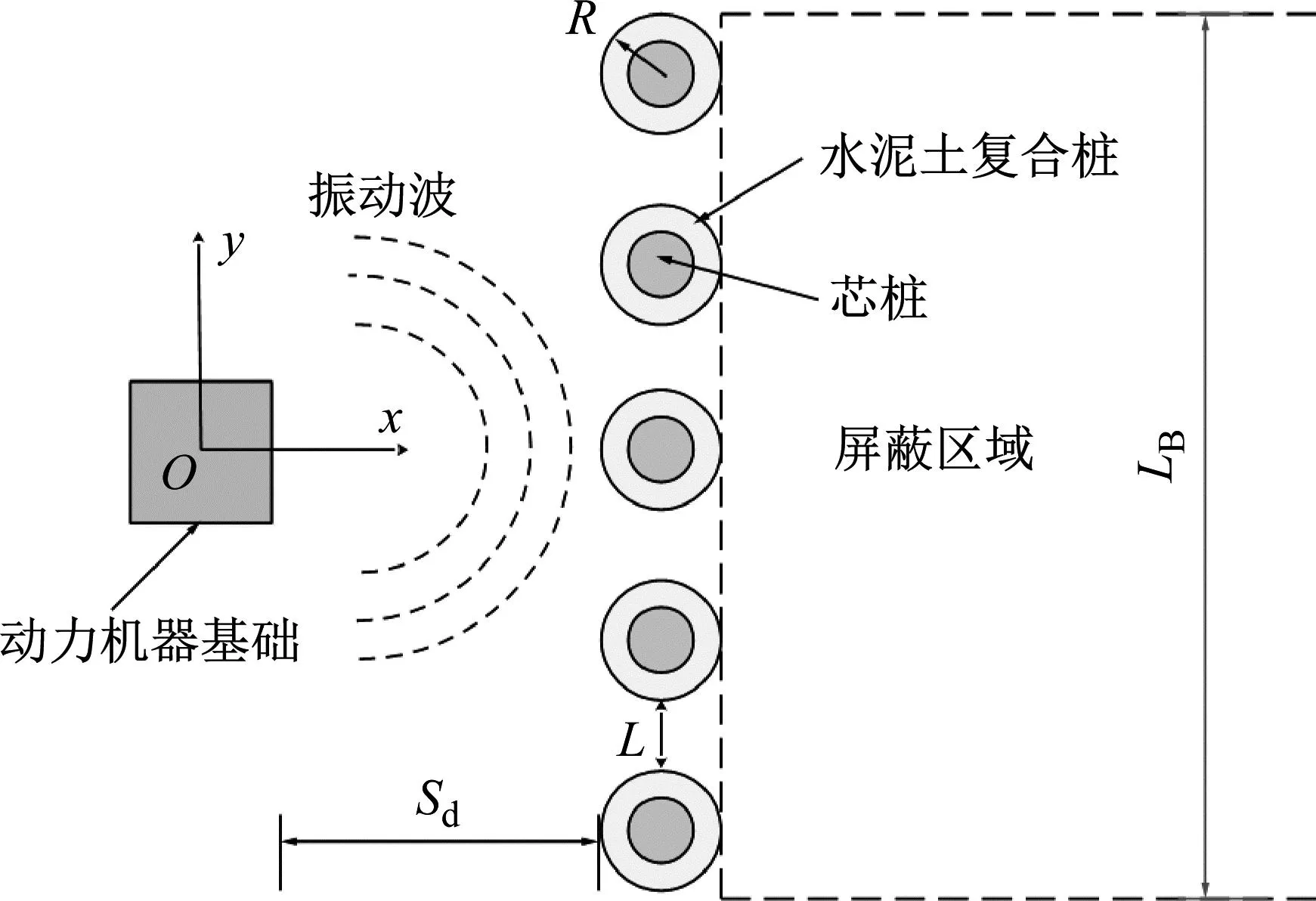
(a) 平面示意图

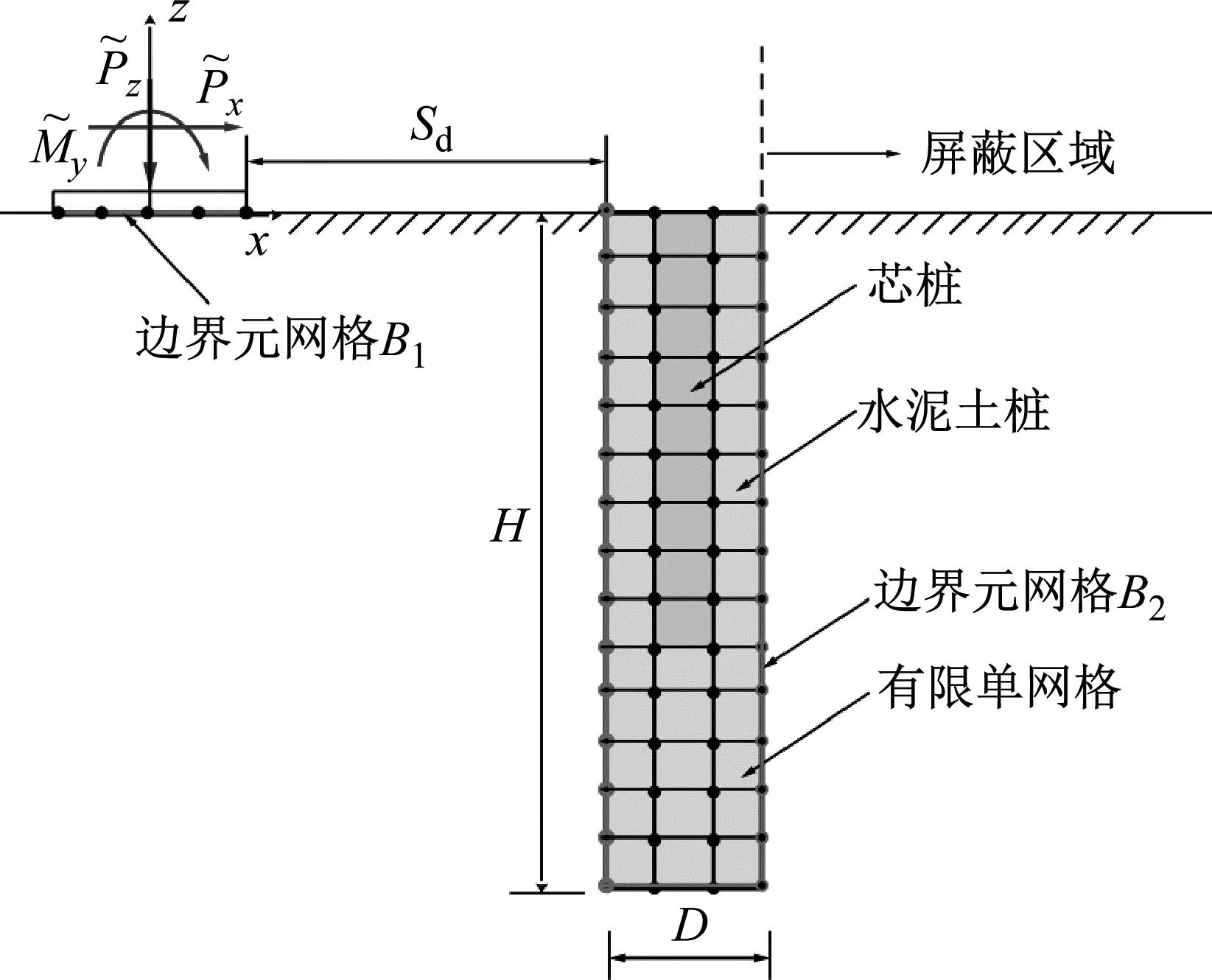
(b) 半解析BEM-FEM的网格划分

2.2 水泥土复合桩振动的FEM方程

水泥土复合桩采用FEM进行建模。考虑到人工振动的位移量级较小,因而不考虑水泥土桩与芯桩接触面的相对滑移和脱开,可采用共用节点方法进行有限元网格划分,见图2(b)。水泥土复合桩振动的FEM方程可表示为

(7)

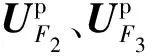
考虑稳态振动问题,为简化起见,省略e-iωt,并采用瑞利阻尼形式,则水泥土复合桩振动的FEM方程可表示为

(8)

式中：“～”为稳态振动量的幅值;Aij=(1-iωβ)Kij-(ω2+iωα)Mij为有限元总体系数矩阵的子矩阵,其中,ω为振动圆频率,α和β分别为瑞利阻尼系数。

2.3 饱和地基-水泥土复合桩接触条件的处理

采用半解析BEM对饱和地基中单排水泥土复合桩的近场隔振问题进行建模时,存在两个接触面,刚性基础-饱和地基接触面和饱和地基-水泥土复合桩接触面。对于刚性基础-饱和地基接触面,按式(3)所示的边界条件进行处理。对于饱和地基-水泥土复合桩接触面,同样不考虑接触面的相对滑移和脱开,且在网格划分时,饱和地基的边界元节点与水泥土复合桩的有限元节点在接触面上一一对应。

考虑水泥土桩不透水的情况,饱和地基-水泥土复合桩接触面的相容条件可表示为

(9)

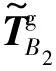
(10)

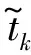
(11)

(12)

将式(11)和式(12)代入式(10),则可得：

(13)

(14)

对比式(14)和式(13)可得

(15)

(16)

按照上述思路,在全部饱和地基-水泥土复合桩接触面边界单元中计算Me,按照边界元节点整体组装位置,最终可得到整体转换矩阵Mg。

考虑到水泥土桩不透水,因此,饱和地基-水泥土复合桩接触面的平衡条件最终可表示为

(17)

2.4 水泥土复合桩近场主动隔振的半解析BEM-FEM耦合方程

根据式(3)、式(9)和式(18)所示的边界条件,并结合式(1)、式(6)和式(8),整理后,最终可得单排水泥土复合桩对动力机器基础振动影响近场主动隔振的半解析BEM-FEM耦合方程为

(18)

对式(18)进行求解即可得到动力机器基础-饱和地基接触面和饱和地基-水泥土复合桩接触面上边界节点的未知量以及刚性基础的位移向量,再根据式(1)和式(6)计算饱和地基边界节点的其他未知量。

为获得饱和地基上任意一点的振动,可采用与式(5)类似的“内点”边界积分方程计算得到

城市里还有一种东西让人无法忍受，那就是无处不在的恶臭味。西瓜皮、各种腐败的食物、死老鼠、宠物的尸体等，在烈日和高温的烘烤下发酵、蒸腾。

(19)

为衡量单排桩的隔振效果,引入位移振幅衰减系数ARF

(20)

为衡量屏障的平均隔振效果,引入平均振幅衰减系数AR

AR=∬A′ARFdxdy

(21)

式中,A′为屏障后屏蔽区域面积,本文取屏障后5倍Rayleigh波长范围作为水泥土复合桩排桩的屏蔽区域。

3 饱和土半解析BEM-FEM耦合方法的算法实现与验证

由第2章可知,本文建立了水泥土复合桩对动力机器基础振动污染近场主动隔振的饱和土半解析BEM-FEM耦合模型,可用于分析均质饱和地基中单排或多排水泥土复合桩的近场主动隔振问题。此外,在饱和土半解析BEM中,本文采用薄层法(thin layer method,TLM)求解得到饱和半空间的动力Green函数,由于TLM可以很方便地获得饱和层状地基的动力Green函数,因此,本文方法也可用于分析层状饱和地基中的屏障隔振问题。

此外,本文算法进行编程实现时,还需要解决算法的计算效率和饱和土半解析BEM-FEM耦合方程的存储等问题。

3.1 饱和土半解析BEM-FEM耦合方法的并行计算

实际工程中,采用水泥土复合桩进行近场主动隔振时,为获得较大面积的屏蔽区域,往往需要数量较多的水泥土复合桩形成单排桩或者多排桩,通常需要划分数目较多的边界单元和边界节点,使得分析问题的计算量和计算耗时急剧增加。

为提高水泥土复合桩排桩近场隔振问题的计算效率,可采用饱和土半解析BEM的SPMD并行算法进行并行计算,可大大降低计算耗时,提高程序的计算效率。

3.2 半解析BEM-FEM耦合方程稀疏矩阵的处理

由式(18)可知,半解析BEM-FEM耦合方程中存在大量的矩阵,其中,除边界元影响系数矩阵HBa和GBa是满秩矩阵外,其他系数矩阵及其子矩阵多为稀疏矩阵或零矩阵形式。将式(18)简写为

(22)

式(22)中,系数矩阵Ω1的子矩阵主要由大量的零子矩阵和有限元总体系数子矩阵Aij组成,其中,Aij也是一个稀疏矩阵,因此,系数矩阵Ω1的大部分元素为零,是一个典型的稀疏矩阵。此外,系数矩阵Ω2和Ω3的大部分子矩阵是零子矩阵和单位子矩阵,也是典型的稀疏矩阵。根据上述分析,Ω1、Ω2和Ω3都是大型稀疏矩阵,如不考虑稀疏矩阵的特点,当屏障隔振系统中的水泥土复合桩数目较多时,极易造成内存不足的现象。

在传统FEM中,一般可采用等半带宽的二维数组或变带宽的一维数组存储总体系数矩阵[34]。然而,由于式(18)是一个半解析BEM-FEM耦合方程,难以采用传统有限元的存储方法来实现。目前,在Fortran或Matlab中,都有专用的稀疏矩阵处理函数,可采用这些函数进行稀疏矩阵处理。例如,Matlab中可采用sparse函数生成稀疏矩阵(零子矩阵和单位子矩阵)或将已有子矩阵转换成稀疏矩阵形式(例如,Mg和nB2等)。然而,当有限元节点数量较大(水泥土复合桩桩数较多)时,有限元总体系数矩阵直接存储时也可能会造成内存不足,从而无法通过sparse函数转换成稀疏矩阵,需要特殊方法生成其稀疏矩阵形式。

实际工程中,当采用多根水泥土复合桩进行隔振时,每根水泥土复合桩型式和尺寸一般均相同。根据有限元基本原理,在总体系数矩阵中,第i根桩节点对第j根桩节点的系数矩阵元素贡献为0(i≠j),且考虑到每根桩有限元网格均相同,因此,有限元方程可表示成如下形式

(23)

(24)

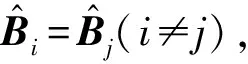
3.3 程序验证

3.3.1 算例验证1

对比计算结果如图3所示。由图可知,本文算法结果与文献[31]算法结果相差不大：①在屏障前都出现了振幅放大现象,等值线分布规律也基本类似,都是以动力机器基础为中心的圆形分布模式;②屏障后不同区域隔振规律也相差不大,同一区域内的隔振效果相差也不大。上述结果表明本文算法是可靠的。此外,本文算法结果与文献[31]也存在一些差异,产生这些差异的原因一方面可能是由于本文水泥土复合桩退化不完全,另一方面可能是FEM中采用瑞利阻尼形式,而BEM中则采用复剪切模量的方式。

(a) ARF的三维曲线图(BEM)

(b) ARF的三维曲线图(BEM-FEM)

3.3.2 算例验证2

当n→0、ρf→0时,饱和地基就退化成弹性地基。Kattis等采用三维BEM研究了弹性地基中多排桩的主动隔振问题,可作为本文算法(将饱和地基退化为弹性地基)的对比算例。计算参数如下：地基土剪切模量Gs=132 MPa,泊松比vs=0.25,密度ρs=1 750 kg/m3;排桩的剪切模量Et=34.29Gs,泊松比vt=0.25,密度ρt=1.37ρs;8根圆桩,桩长1.0λR,桩径0.2λR,桩间净距0.1λR,动力机器基础距屏障距离1.5λR。对比计算结果如图4所示。

图4 本文计算结果与Kattis等结果对比

由图4可知,本文计算结果与Kattis等结果在ARF的分布规律上非常近似,仅在部分区域ARF量值上稍有差异,产生这种差异的原因一方面是由于FEM计算精度问题,另一方面可能是饱和地基退化问题。

4 单排水泥土复合桩近场主动隔振效果分析

地铁列车、重载货车等交通诱发环境振动的低频部分主要分布在10～20 Hz。排桩屏障可以设置较大桩长,因而更加适合对这种低频振动进行隔振。为简化分析,本文仅考虑对f=10 Hz的低频稳态振动进行隔振效果分析。

对于淤泥和淤泥质土等饱和软黏土,其Rayleigh波波速VR一般小于100 m/s。本文取饱和土的VR=100 m/s,Rayleigh波波长为λR=10 m。饱和土地基的材料参数如表1所示。

表1 饱和土地基的材料参数

本文采用复剪切模量来考虑饱和土材料阻尼的影响,取材料阻尼ξ=0.02。

采用水泥土复合桩构建单排桩隔振屏障系统时,水泥土复合桩桩长h1取15 m,水泥土桩桩径r1取0.5 m。基本分析工况时,芯桩为PHC管桩,芯桩桩径r2为0.25 m,根据GB 13476—2009《先张法预应力混凝土管桩》[34],选取管桩型号为PHC500A100。水泥土复合管桩截面如图5(a)所示。芯桩长度考虑两种情况,等长芯桩和短芯桩,如图5(b)和(c)所示。其中,短芯桩的芯桩长度h2取12 m。此外,对于单排水泥土复合桩屏障,基本分析工况时,桩数N取5,桩间净距l取2.0 m。

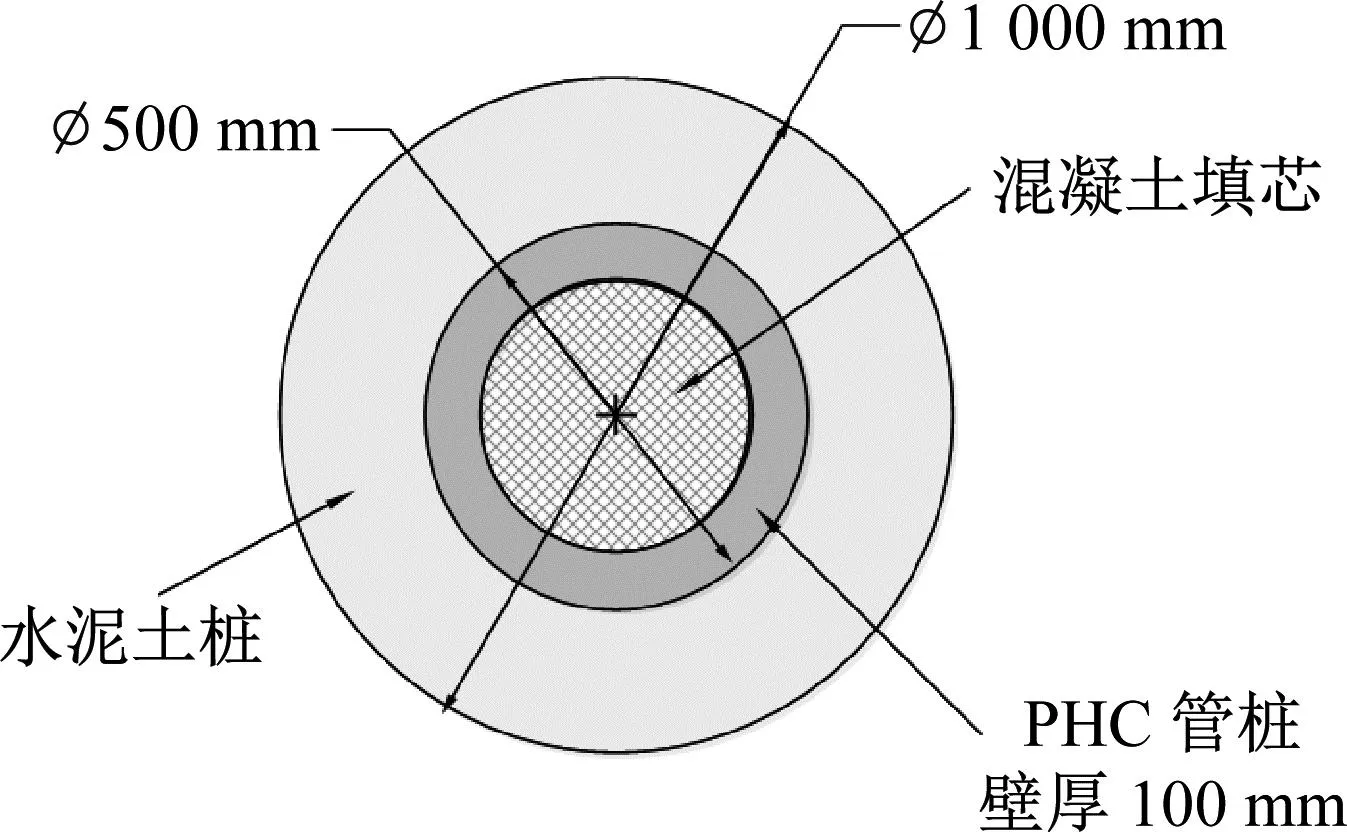
(a) 管桩水泥土复合桩的截面形式

(b) 等长芯桩

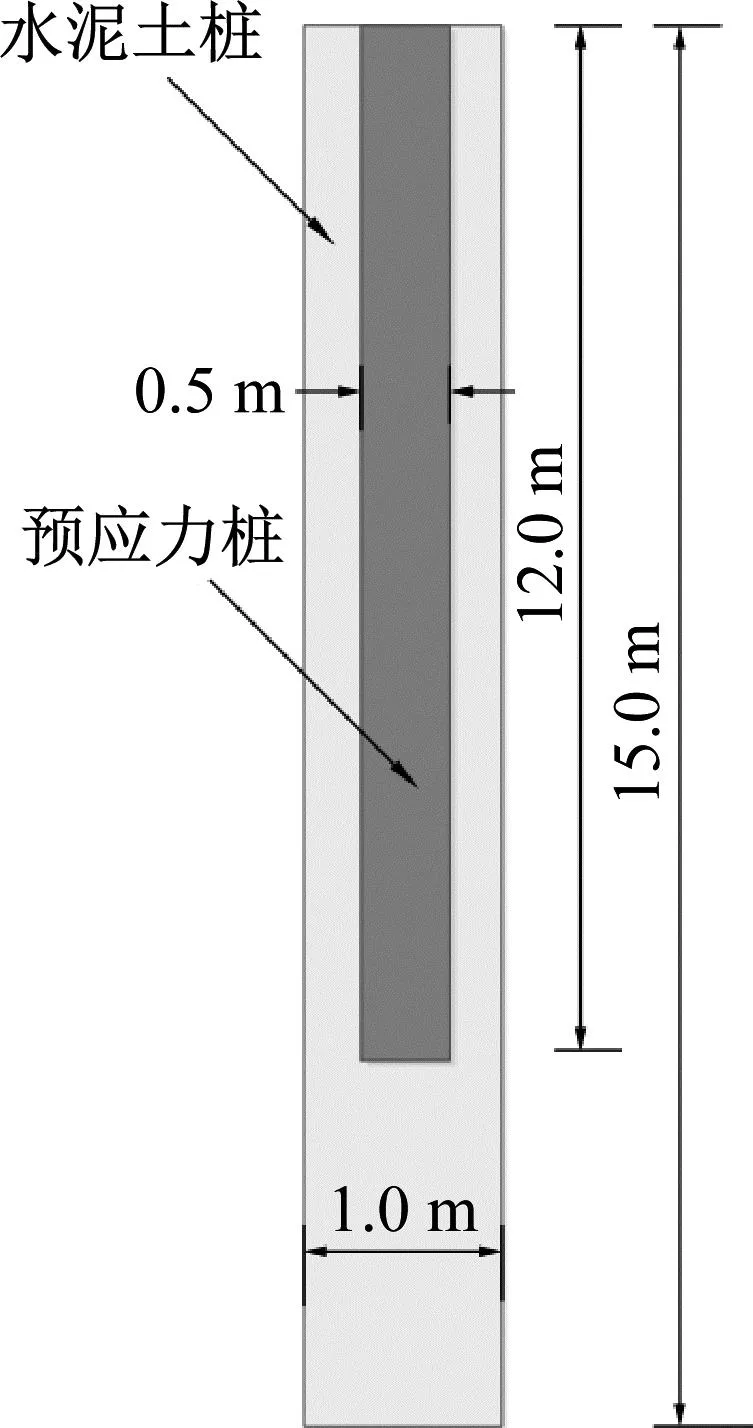
(c) 短芯桩

对于水泥土复合桩,水泥土的弹性模量Ec=120 MPa[35],密度ρc=19 kN/m3,泊松比vc=0.3;预制芯桩(PHC管桩)的弹性模量Ep=38 GPa,密度ρp=2 500 kg/m3,泊松比vp=0.22。

采用饱和土Rayleigh波波长λR作为无量纲化条件,基本工况下,单排水泥土复合桩的无量纲化参数如表2所示。

表2 单排水泥土复合桩的无量纲参数

4.1 单排水泥土复合桩的主动隔振效果分析

4.1.1 基本工况下的屏障隔振效果

基本工况下,单排水泥土复合桩的隔振效果如图6和图7所示。

(a) 振幅衰减系数ARF的三维曲面图

(b) 振幅衰减系数ARF沿X*轴分布图

(a) 振幅衰减系数ARF的三维曲面图

(b) 振幅衰减系数ARF沿X*轴分布图

图6和图7分别为等长芯桩和短芯桩条件下单排水泥土复合管桩的振幅衰减系数ARF图,其中,X*=x/λR和Y*=y/λR分别为垂直于单排桩方向和沿单排桩方向的无量纲坐标,x和y坐标如图2(a)所示。由图可知,对于单排水泥土复合桩,屏障前ARF均出现大于1的情况(等长芯桩约为1.9,短芯桩约为1.5),这表明动力机器基础振动产生的一部分入射弹性波被单排水泥土复合桩反射回去,反射波与入射波在屏障前相互叠加,从而在特定区域产生振动放大现象;屏障后振幅衰减系数ARF均小于1,表明单排水泥土复合桩能够有效地对动力机器基础振动产生的环境振动进行隔振,仅有小部分弹性波透射到屏蔽区域。屏障后隔振效果最佳的区域大致分布在屏障后约1～2λR和3～4λR(等长芯桩)区域、1～2λR(短芯桩)范围内。

由于单排桩设置在振源附近,属于近场主动隔振,因此,在图2(a)给出的屏蔽区域内,中心区域(C*=0,其中,C*=y/LB,LB为屏障总长度,如图2(a)所示)的隔振效果与屏障边缘区域(C*=1.0)的隔振效果相差不大,这主要是由于动力机器基础振动所产生的弹性波(距振源较近时以体波为主)以半球形形态向四周传播,单排桩实际的屏蔽区域要大于图2(a)中屏蔽区域范围,这与主要对入射Rayleigh波隔振的单排桩远场被动隔振情况不同。

此外,当水泥土桩桩长一定的情况时,等长芯桩的平均振幅衰减系数AR约为0.326,而短芯桩时的平均隔振效果AR约为0.690,这表明在水泥土复合桩排桩隔振系统中,芯桩长度是一个非常重要的控制参数,芯桩长度越大,屏障的隔振效果越好。因此,实际工程中建议水泥土复合桩屏障的预制芯桩与水泥土桩等长设置。

综上可知,当动力机器基础振动产生的弹性波入射到单排水泥土复合桩位置时,由于水泥土、预应力混凝土管桩以及饱和地基土之间的材料差异性,使得弹性波在水泥土-饱和地基界面上和水泥土-管桩界面上产生了复杂散射现象,特别是在水泥土复合桩内部,管桩对弹性波的散射现象更加强烈,正是这种复杂的散射现象使得仅有一小部分弹性波可以穿过单排水泥土复合桩透射到屏蔽区域。此外,对于短芯桩的情况,由于芯桩长度较短,水泥土复合桩内部的一部分散射波可经由水泥土复合桩底部的薄弱区域(纯水泥土区域)透射到屏障后的屏蔽区域,而等长芯桩不存在纯水泥土的薄弱区域,因而对弹性波的散射效果显著优于短芯桩的情况。

4.1.2 水泥土复合桩屏障中管桩的影响分析

为分析水泥土复合桩中预制芯桩(PHC管桩)对屏障隔振效果的贡献,本文还计算了纯水泥土桩(未设置芯桩)的工况。此外,采用管桩水泥土复合桩构建隔振屏障时,考虑到不同的施工工艺,PHC管桩中心可灌注混凝土,也可不做填芯处理;当PHC管桩底部不封底时,PHC管桩中心则被水泥土充填。分别建立BEM-FEM耦合模型,对比分析上述条件对单排管桩水泥土复合桩隔振效果的影响规律,计算结果如图8所示。

图8 不同工况下单排管桩水泥土复合桩的隔振效果

由图8可知,等长芯桩水泥土复合桩的隔振效果要远优于短芯桩的情况,平均振幅衰减系数AR要减小0.4左右。而在等长芯桩条件下,PHC管桩填芯与否对屏障的隔振效果基本无影响。此外,当不设置芯桩时,即纯水泥土桩的隔振效果相对较差(AR>0.85),无法满足正常隔振的需求,这表明在水泥土复合桩隔振系统中,预制芯桩(PHC管桩)起到关键的隔振作用,这主要得益于PHC管桩极高的弹性模量。

4.2 单排水泥土复合桩隔振系统几何参数的影响

对于单排水泥土复合桩近场主动隔振系统,排桩的桩数N、桩间净距l以及屏障距振源的距离Sd是隔振系统构建时重要的技术参数。为构建隔振效果良好的水泥土复合桩隔振系统,本节主要分析上述三个因素对隔振效果的影响。

4.2.1 排桩桩数N的影响

在单排桩隔振系统设计中,排桩桩数N不仅会影响屏蔽区域的范围,还会影响排桩屏障的隔振效果。为分析桩数N对单排水泥土复合桩隔振效果的影响,N取2～9,计算结果如图9和图10所示。

图9为单排管桩水泥土复合桩桩数N=9时振幅衰减系数ARF的等值线图。由图9可知,无论是等长芯桩(h2=15 m)还是短芯桩(h2=12 m),屏障后ARF的分布规律大致相同：随着距屏障距离的变化,ARF呈一定的波动起伏状态;隔振效果最佳的区域大致位于2～3λR;等长芯桩屏障后ARF普遍小于短芯桩的情况,表明等长芯桩的隔振效果更佳。

图10为单排管桩水泥土复合桩平均振幅衰减系数AR随桩数N的变化曲线。由图10可知,对于等长芯桩(h2=15 m),随着单排桩桩数N的增加,屏障的整体隔振效果逐渐提高,当N超过5时,屏障平均隔振效果AR基本稳定在0.32左右。而对于短芯桩(h2=12 m),当桩数较少时,屏障整体隔振效果也随着桩数N的增加而提高,但提高幅度不大,且当桩数超过4后,屏障的平均隔振效果基本无变化。

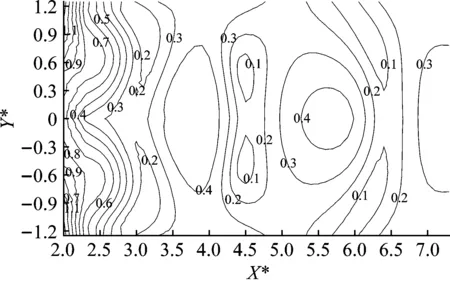
(a) 等长芯桩

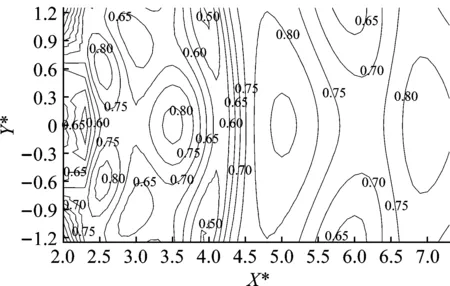
(b) 短芯桩

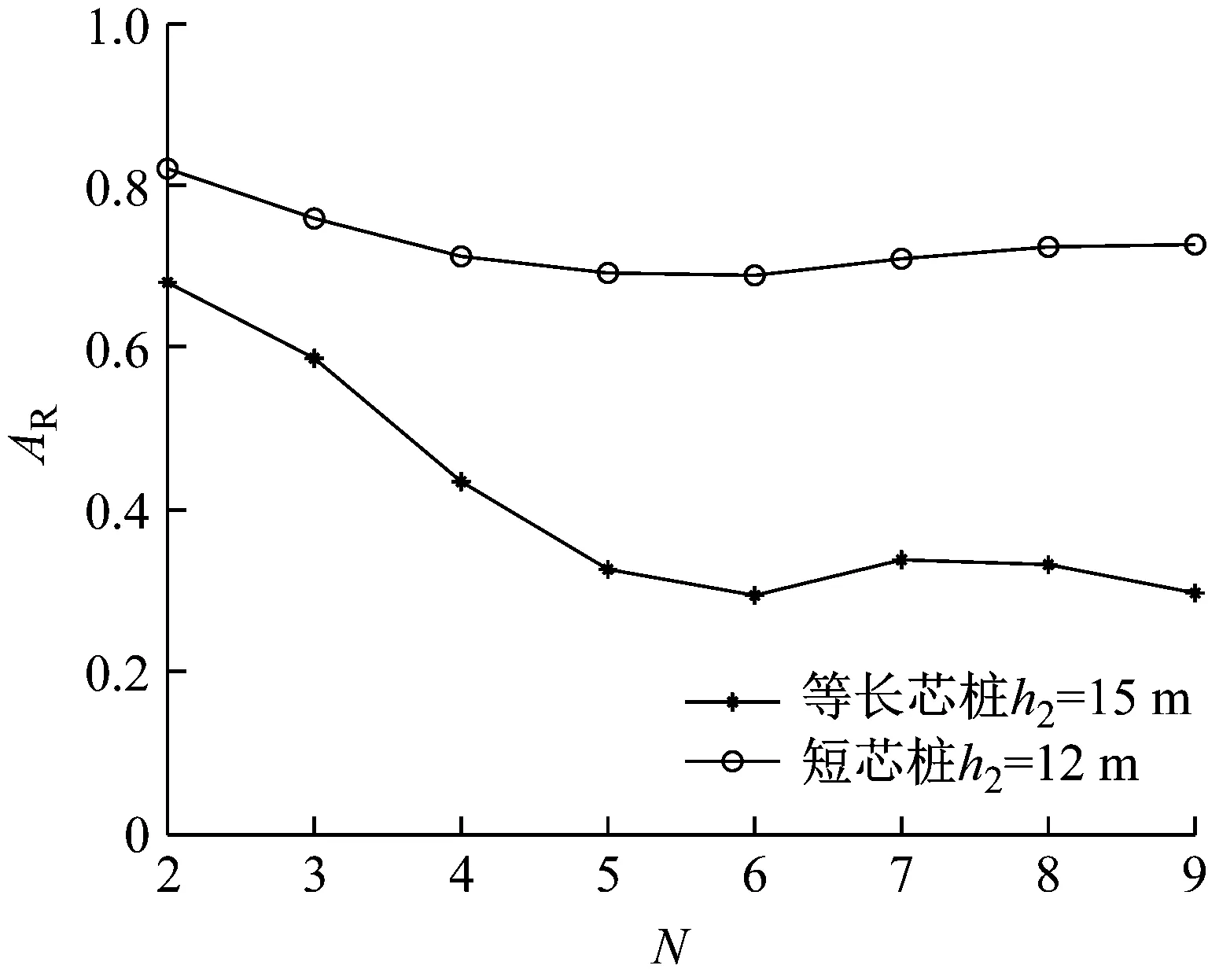
图10 水泥土复合管桩桩数N对AR的影响

综上,对于单排管桩水泥土复合桩隔振系统,除桩数较小的情况外,桩数对屏蔽区域的平均隔振效果影响相对较小,实际工程中,可根据需要屏蔽区域范围选择合理的桩数。

4.2.2 桩间净距l的影响

已有研究表明,桩间净距l对隔振效果有较大影响,当l较大时,屏障往往难以呈一个整体对入射弹性波进行散射。与传统排桩隔振系统相比,水泥土复合管桩对弹性波的散射作用更为复杂,桩间净距l对隔振效果的影响需要进一步探讨。为此,无量纲桩间净距l*分别取0.10、0.15、0.20、0.25、0.30和0.35,计算结果如图11和图12所示。

(a) 等长芯桩(h2=15 m)

(b) 短芯桩(h2=12 m)

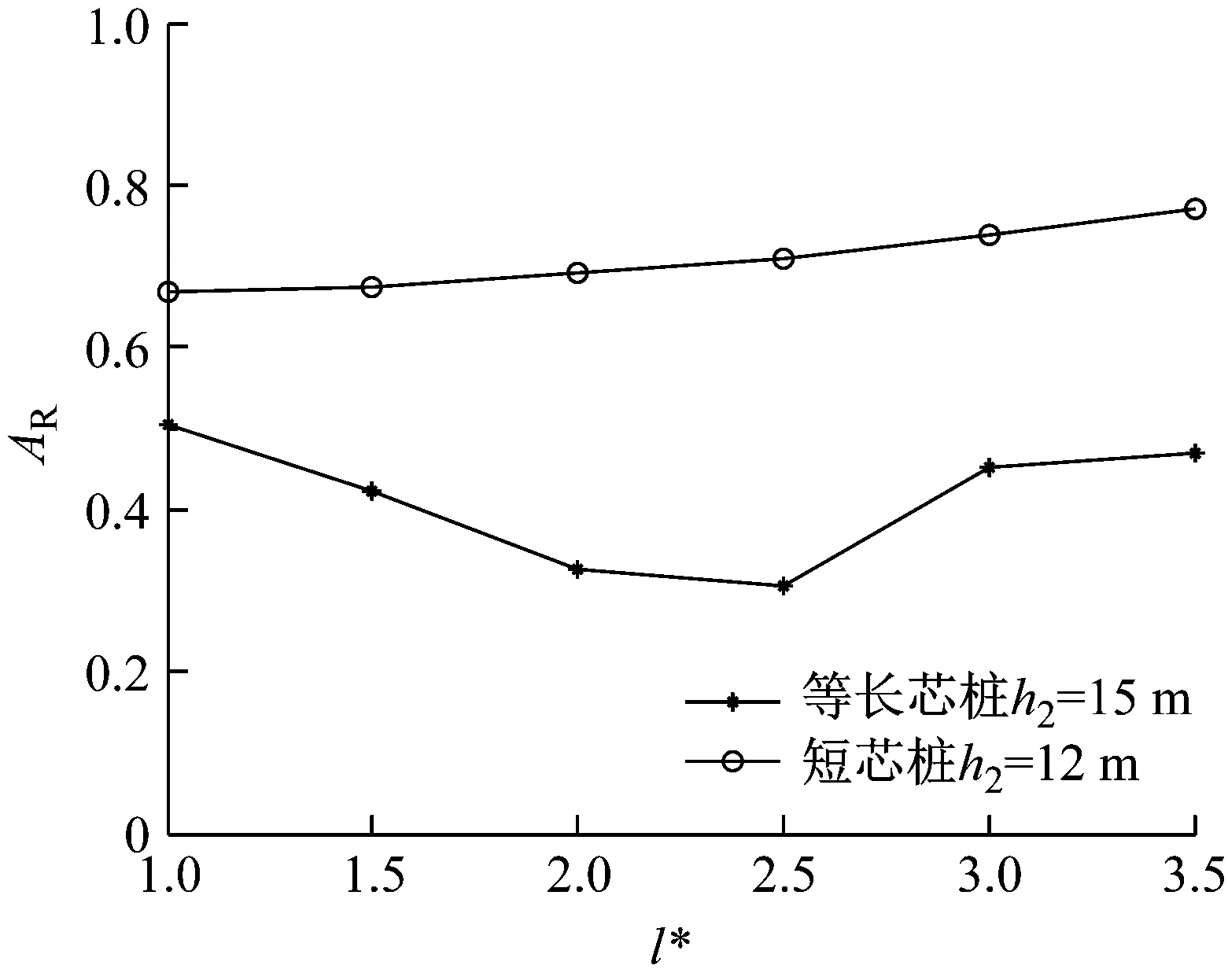
图12 水泥土复合桩桩间净距l*对AR的影响

图11为单排水泥土复合桩桩间净距l*=0.35时振幅衰减系数ARF的等值线图。由图11可知,与传统混凝土桩排桩相比,桩间净距l*对单排水泥土复合桩主动隔振效果的影响相对较小,桩间净距取较大值(l*=0.35)时,单排水泥土复合桩仍能呈一个整体对动力机器基础产生的弹性波起到散射作用。

图12为单排水泥土复合桩桩间净距l*对平均振幅衰减系数AR的影响曲线。由图12可知,短芯桩(h2=12 m)时,单排桩的隔振效果随桩间净距l*增大而降低,但降低幅度不大;等长芯桩(h2=15 m)时,单排桩的隔振效果随桩间净距的增大呈先提高后降低的趋势,AR的变化幅度在0.2左右,桩间净距l*在2.0～2.5范围时隔振效果最佳。

综上,与传统混凝土桩排桩不同,桩间净距l*对于单排管桩水泥土复合桩隔振效果的影响较为复杂,这表明单排管桩水泥土复合桩对入射弹性波的散射机理更为复杂,但总体而言,较小桩间净距不一定取得更好的隔振效果,实际工程中建议桩间净距l*取2.0～2.5。

4.2.3 距振源距离Sd的影响

(a) 等长芯桩

(b) 短芯桩

图14 水泥土复合桩距振源距离对AR的影响

4.3 不同预制芯桩水泥土复合桩的隔振效果分析

在水泥土复合桩中,芯桩除采用PHC管桩外,还可以采用其他型式的预制桩,例如空心方桩等。为探讨不同类型芯桩水泥土复合桩的近场被动隔振效果,本文选取预应力混凝土空心方桩、预应力混凝土实心桩(圆桩、方桩)以及预应力混凝土异形桩(X型桩、十字型桩)。芯桩为空心方桩时,根据JG/T 197—2018《预应力混凝土空心方桩》[36],选取空心方桩型号为PS-500-310-95-12(15)-A,如图15(a)所示。当芯桩为预应力混凝土实心桩时,对于方桩,边长为0.5 m,对于圆桩,直径为0.5 m,如图15(b)和(c)所示。此外,考虑两种异形桩的形式,一种为十字型桩,一种为X型桩,具体尺寸如图15(d)和(e)所示。

(a) 空心方桩

(b) 实心方桩

(c) 实心圆桩

(d) 十字型桩

(e) X型桩

为简化分析,本小节仅考虑等长芯桩的工况,计算结果如图16所示。由图16可知,当预制芯桩外轮廓尺寸相同时,不同截面预制芯桩的水泥土复合桩屏障的隔振效果相差不大,平均振幅衰减系数AR相差在0.08以内。因此,实际工程中,可根据当地实际条件选择合适的芯桩来构建水泥土复合桩屏障系统。

4.4 不同土层条件下水泥土复合桩的隔振效果分析

前文主要分析了饱和地基条件下单排水泥土复合桩的隔振效果。实际工程中,当地下水位位于地面下一定深度时,上层土体处于非饱和状态,而下层土体处于饱和状态,是一种典型的二元地基形式。为检验二元地基条件下单排水泥土复合桩隔振效果,考虑地下水水位埋深10 m的工况条件,单排水泥土复合桩参数见表2。本文采用3.3节中饱和土退化方法实现对非饱和土的模拟,计算结果如图17所示,同时给出非饱和土地基的隔振效果。

图16 水泥土复合桩芯桩型式对AR的影响

(a) 上层非饱和+下层饱和地基

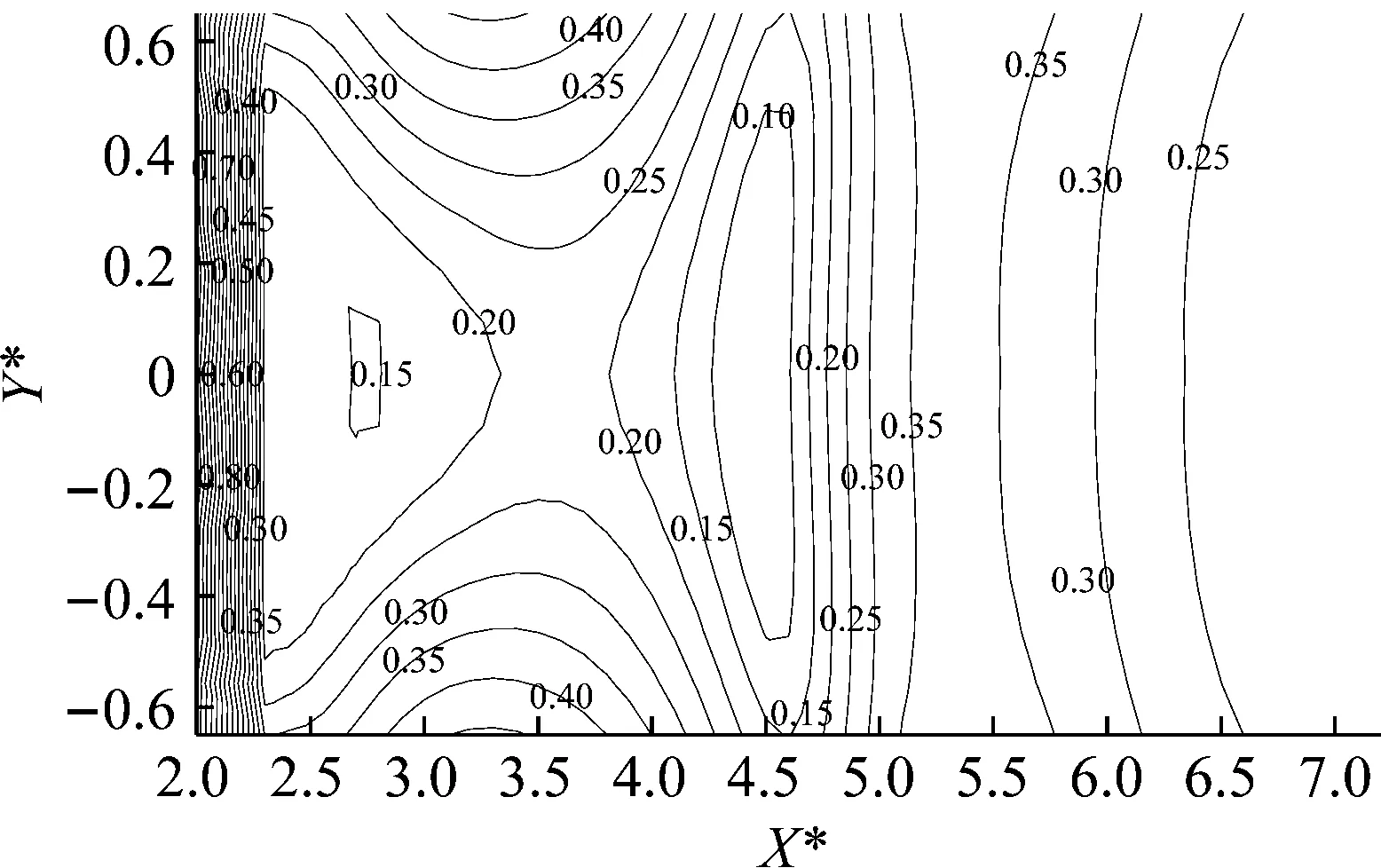
(b) 非饱和地基

由图17可知,对于上层非饱和下层饱和的二元地基,单排水泥土复合桩仍可以起到较好的隔振作用,且其隔振效果(AR=0.26)稍好于均质饱和地基(AR=0.32)的情况。此外,对于非饱和土地基,单排水泥土复合桩也可以起到较好的隔振作用,平均隔振效果(AR=0.27)与二元地基相差不大。

5 结 论

针对城市中的人工振动污染特别是交通引起的环境振动污染问题,本文提出一种单排水泥土复合桩近场主动屏障隔振体系,建立了饱和地基中单排水泥土复合桩对动力机器基础振动近场主动隔振的半解析BEM-FEM耦合方法,对单排水泥土复合桩的近场主动隔振问题进行了详细研究。主要结论如下：

(1) 饱和地基中单排水泥土复合桩能够对动力机器基础产生的环境振动起到较好的隔振作用;与水泥土桩屏障相比,预制芯桩在水泥土复合桩隔振体系中起到关键作用;等长芯桩水泥土复合桩的隔振效果要优于短芯桩的情况,建议工程中采用等长芯桩水泥土复合桩来构建隔振屏障体系。

(2) 在单排管桩水泥土复合桩隔振系统中,等长芯桩单排管桩水泥土复合桩的隔振效果随单排桩桩数的增加逐渐变好,而短芯桩隔振效果的提高幅度相对较小;过小的桩间距并不一定取得更好的隔振效果,建议桩间净距l取2.0～2.5λR;此外,随着单排水泥土复合桩距振源距离的增加,屏障隔振效果逐渐降低,但降低幅度相对较小。

(3) 在单排水泥土复合桩隔振系统中,预制芯桩外轮廓尺寸相同时,芯桩型式对隔振效果的影响相对较小,实际工程中可根据当地情况选择合适的预制芯桩型式。