湿热环境下玻/碳纤维混杂复合材料梁阻尼特性的细观力学分析

邵士儒, 王 洋, 孙双双

(青岛科技大学 机电工程学院, 山东 青岛 266061)

随着科技发展,汽车、军工、航空航天等众多领域对振动控制和噪音控制的要求越来越高,材料阻尼特性方面的研究愈发重要。纤维增强树脂基复合材料相较于传统金属材料具有优异的阻尼性能,在减振降噪方面可发挥重要作用[1]。尤其是纤维混杂复合材料,可设计性高,多种纤维混杂使用优势互补,具有广阔的发展前景。纤维增强复合材料的阻尼损耗因子取决于一系列参数,包括材料组分特性、纤维体积分数、铺层角度、铺层厚度、铺层顺序、温度、湿度等。在高温、潮湿等恶劣环境下,纤维增强复合材料的物理性能发生明显变化[2],对阻尼性能影响较大,且通常阻尼器工作环境复杂,因此,研究湿热环境下混杂复合材料的细观阻尼特性具有重要意义。

目前,国内外众多学者从细观力学角度研究了组分性能及含量、铺层参数等对纤维增强复合材料阻尼特性的影响。例如,Wang等[3]基于能量耗散原理建立了单一纤维增强复合材料的阻尼预测模型,并通过试验研究了纤维和树脂基体体积分数对纤维增强复合材料阻尼比的影响。结果表明：树脂基体的体积分数对阻尼性能起重要作用,随着树脂基体体积分数的增大,纤维增强复合材料的损耗因子呈现出增大的趋势;随着纤维体积分数的增加,界面结合强度降低,阻尼性能越好。Rahman等[4]通过试验研究了纤维体积分数和纤维铺设角度对亚麻纤维增强复合材料阻尼特性的影响。结果表明：亚麻纤维铺层角度对阻尼的影响远高于纤维体积分数的影响,铺层角度在45°左右时损耗因子达到最大,继续增大铺设角度,损耗因子略有下降。Cai等[5]建立了复合材料层合板的粘弹性阻尼模型,并通过试验验证了该阻尼模型的准确性。文中认为随着纤维体积分数、层数和层厚的增加,复合材料层板的阻尼比增大,0°层数越多,离最外层越近,阻尼比越大。Yim等[6]运用解析法建立了细观力学的阻尼预测模型以研究纤维体积分数对石墨/环氧树脂复合材料层合梁阻尼特性的影响,并将计算结果与Ni-Adams法进行对比验证了理论模型的可靠性。Cheour等[7]通过自由弯曲振动试验研究了吸湿环境下纤维铺设角度对亚麻复合材料和玻璃/亚麻纤维混杂复合材料阻尼性能的影响。Li等[8]基于经典层合板理论、复模量法和应变能法建立了纤维增强复合材料在热环境下的非线性动力学理论模型。结果表明：碳纤维复合材料的损耗因子随着温度的升高而增大,阻尼较大的铺层方式下,对温度的升高并不敏感。Assarar等[9]采用试验法与有限元法结合,研究了碳/亚麻混杂复合材料铺层顺序对阻尼等特性的影响,认为亚麻纤维铺层在外侧时,材料阻尼较高,弯曲模量较低。Sefrani等[10]用试验测得不同铺层角度的单层板力学性能随温度变化关系,用模态分析法计算了单层板的震动横向位移,最终根据能量耗散原理得到单层板损耗因子随温度变化关系。Li[11]建立了纤维增强陶瓷基复合材料C/SiC在温度影响下的细观阻尼预测模型,建立了材料阻尼、材料内部损伤与温度之间的关系。Kang等[12]采用五种不同铺层角度的碳纤维增强复合材料试件在变温环境下进行单轴振动试验,计算了阻尼系数,认为纤维角度为0°时阻尼非线性最低。

通过查阅国内外文献发现,目前的研究工作大多是在常温干态下研究复合材料纤维体积分数、铺设角度及铺层顺序等参数对阻尼特性的影响,考虑湿热影响的文献较少。Sefrani等虽考虑了温度的影响,但文中是通过试验法测得复合材料力学性能随温度变化关系,进而进行理论分析,没有建立完整的湿热状态下阻尼预测理论模型。且文中研究对象为玻璃纤维单层板,没有考虑混杂复合材料铺层顺序等方面影响。Li研究对象为陶瓷基复合材料,主要研究内容是不同纤维体积分数、裂纹间距及界面粘结性能下,阻尼性能随温度的变化关系,与本文研究对象及内容均不同。Kang等用试验法研究了碳纤维复合材料阻尼与温度的关系。目前关于复合材料阻尼方面的研究缺乏完整的湿热环境下的理论模型,不能系统、全面地描述复合材料湿热环境下的阻尼特性,尤其是纤维混杂复合材料的湿热阻尼性能研究更是鲜有报道。

本文将以玻/碳纤维混杂对称层合梁为研究对象,基于细观力学,利用能量耗散原理及宏观应变能法建立湿热环境下其阻尼预测模型,分析湿热环境对材料阻尼特性的影响机理,研究湿热环境下纤维铺层顺序、铺设角度及体积分数对玻/碳纤维混杂复合材料层合梁阻尼性能的影响规律。

1 理论分析

玻/碳纤维混杂层合梁在湿热环境下受力示意图及横截面示意图,如图1所示。图1(a)中a、b、h分别为梁的长、宽、高,Mx为所受弯矩,图1(b)由下至上依次为层合梁第1～n层,图示第1和第n层为碳纤维铺层,第2和第n-1层为玻璃纤维铺层。

(a) 湿热环境下受力示意图

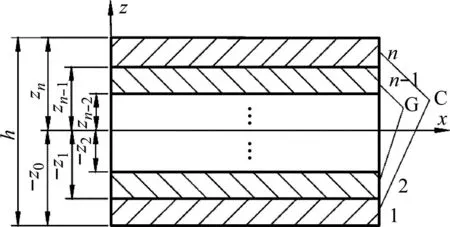
(b) 横截面示意图

当复合材料层合梁受x方向弯矩Mx作用做自由弯曲振动时,其损耗因子η可以表示为[13]

(1)

式中：ΔU为耗散的应变能;U为储存的应变能。下面分别介绍其计算过程。

将层合梁一个微元体δV内的纵向、横向及面内剪切耗散的应变能分别记为δ(ΔU1)、δ(ΔU2)及δ(ΔU12),其宏观应变能法计算表达式如下

(2)

式中,σiHT和εiHT(i=1,2,12)分别为层合梁任意一点材料主坐标系下纵向、横向及面内剪切湿热应力和应变。ηi(i=1,2,12)分别为这一点所在单层板的纵向、横向及面内剪切损耗因子,其计算公式分别为[14]

(3)

式中：ηfE和ηmE分别为纤维和基体拉压损耗因子;ηfG和ηmG分别为纤维和基体剪切损耗因子;Ef和Em分别为纤维和基体弹性模量;Vf和Vm分别为纤维和基体体积分数。将式(2)三个量分别沿层合梁积分并相加,即可得到层合梁整体耗散的应变能为

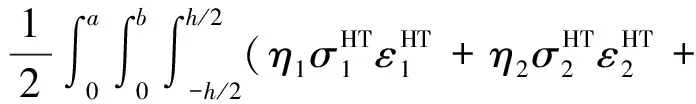
(4)

复合材料单层板的湿、热膨胀系数、工程弹性常数及泊松比与组分性能及体积分数关系如下[15-17]

(5)

式中：αf和αm分别为纤维和基体的热膨胀系数;νf和νm分别表示纤维和基体的泊松比;βm为基体湿膨胀系数;ρ和ρm分别为层合梁和基体的密度。Kumar等[18]建立的单层板的材料参数随温度和湿度的变化关系为线性函数,计算简单且准确度高,因此本文借鉴此方法进行计算,表达式如下

(6)

(7)

单层板的二维刚度矩阵计算公式为

(8)

联立式(7)、(8)并结合麦克斯韦定理,可得湿环境下单层板的刚度矩阵[QT]为

(9)

离轴刚度矩阵为

(10)

式中：[Г]为坐标转换矩阵;[Г]T表示其转置。湿热环境下弯曲刚度矩阵[DT]为

(11)

纤维混杂复合材料层合梁的湿热内力矩分别为

(12)

式中,{α}k和{β}k分别为第k层整体坐标系下的热、湿膨胀系数。其计算公式为

(13)

由于本文研究对象为对称铺设层合梁,故湿热内力矩为0,耦合刚度矩阵[B]全为0。将湿热环境下弯曲刚度矩阵的逆矩阵记为[DT]-1,由于梁所受载荷仅为x方向的弯矩Mx,因此湿热环境下层合梁第k层的应变为

(14)

将式(11)～(13)代入式(14)可得湿热环境下复合材料层合梁整体坐标系下每一层的应变,通过坐标转换进一步得材料主方向的应变为

(15)

纤维混杂复合材料第k层材料主坐标系下湿热应力-应变关系为

(16)

将式(4)、(15)、(16)代入式(3),可得湿热环境下复合材料层合梁受弯矩作用时整体损耗应变能。

湿热环境下复合材料层合梁储存的应变能为

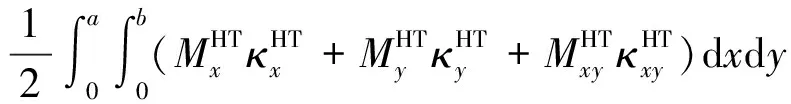
(17)

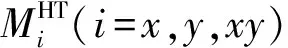
(18)

式中,{M}为层合梁弯矩载荷列向量,本文仅有Mx不为0。将式(4)、(17)代入式(1)可得湿热环境下基于细观力学的复合材料层合梁损耗因子。

2 程序设计及验证

根据第1章所推导的理论公式编写MATLAB程序,程序分为主程序和子程序两个部分,主要流程如图2所示。主程序主要用来控制参数变化并循环,为研究损耗因子的影响因素,将纤维体积分数、铺设角度、温度、吸水浓度等参数在主程序中输入,并且每次控制一个参数为变量,随着循环逐渐递进。子程序接收这些参数,计算各种条件下材料的损耗因子,再将结果输出到主程序。最后根据各种不同条件及对应的损耗因子,绘制图像。

图2 计算损耗因子程序主要流程

算例1常温干态环境下碳/亚麻混杂纤维复合材料损耗因子计算

Assarar等研究了常温干态下碳/亚麻混杂纤维复合材料不同铺层方式损耗因子的变化规律,表1为文献中碳纤维和亚麻纤维单层板工程参数,C代表碳纤维层,F代表亚麻纤维层。利用本文理论计算不同铺层方式下材料的损耗因子,并将结果与文献[9]结果对比,如图3所示。由图3可知,本文计算结果与文献结果变化趋势相同,单层板结果一致性非常好,层合梁结果略有偏差,但偏差在5%以内,因此本文理论模型可以较准确预测混杂纤维层合梁损耗因子变化规律。

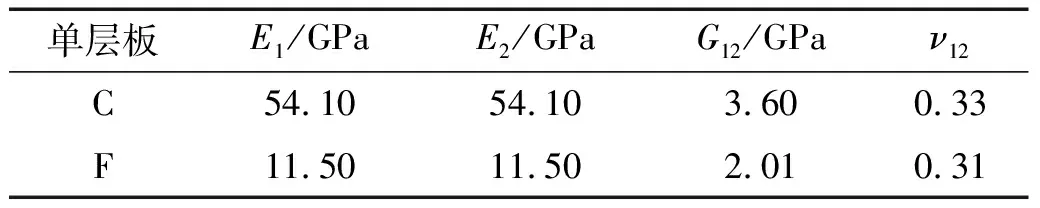
表1 碳纤维及亚麻纤维单层板工程常数

算例2干态环境考虑温度影响的玻璃纤维单层板损耗因子计算

Sefrani等研究了玻璃纤维复合材料铺层角度及温度对损耗因子的影响,其中不同温度下纵向、横向及剪切损耗因子η1、η2、η12,如表2所示。玻璃纤维单层板各方向弹性模量分别为E1=29.9 GPa、E2=5.85 GPa、G12=2.45 GPa,泊松比ν21=0.24。将这些材料参数代入本文理论模型及计算程序,分别计算温度为25 ℃、50 ℃、60 ℃、70 ℃、90 ℃及100 ℃,纤维角度为0°～90°时材料的损耗因子,所得结果与文献[10]中结果对比如图4所示。由图4可知,本文理论解与文献[10]试验解的吻合程度非常好,而且优于文献[10]理论解与试验解的吻合程度。由此说明,本文基于细观力学考虑湿热影响的阻尼预测模型及计算程序具有较高的计算精度。

图3 不同铺层方式层合梁的损耗因子本文解与文献[9]解对比

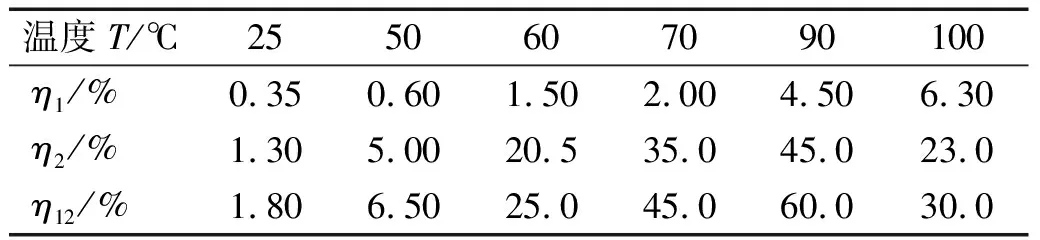
表2 不同温度下玻璃纤维复合材料各方向损耗因子

3 数值模拟与讨论

本章将针对玻/碳纤维混杂复合材料层合梁在湿热环境下的阻尼特性进行一系列研究,梁的长a=180 mm,宽b=10 mm,文中以C代表碳纤维铺层,G代表玻璃纤维铺层,每个铺层厚度均为0.125 mm,无特别说明则纤维体积分数均为35%,铺层角度均为0°。玻璃纤维、碳纤维和树脂基体的材料参数如表3所示。湿热环境下单层复合材料力学性能衰减模型中的湿热常系数如表4所示。

3.1 湿热环境对玻/碳纤维混杂复合材料阻尼特性的影响机理

3.1.1 湿热环境对玻/碳纤维混杂复合材料弯曲刚度的影响

图4 本文解与文献[10]中理论解及试验解结果对比

湿热环境对复合材料的影响首先体现在对单层板弹性模量E1、E2、G12的影响,进而影响层合梁的力学性能。本文的层合梁模型所受外载荷为仅为x方向的弯矩Mx,由第1节可知层合梁弯曲刚度矩阵D对损耗因子至关重要,因此本节将分别研究[C2G2]s、[G2C2]s、[CGCG]s、[GCGC]s四种不同铺层方式下的D11、D12、D22受湿热环境影响的变化规律,计算结果如表5所示。

表3 玻璃纤维、碳纤维和树脂基体的材料参数

表4 湿热常系数

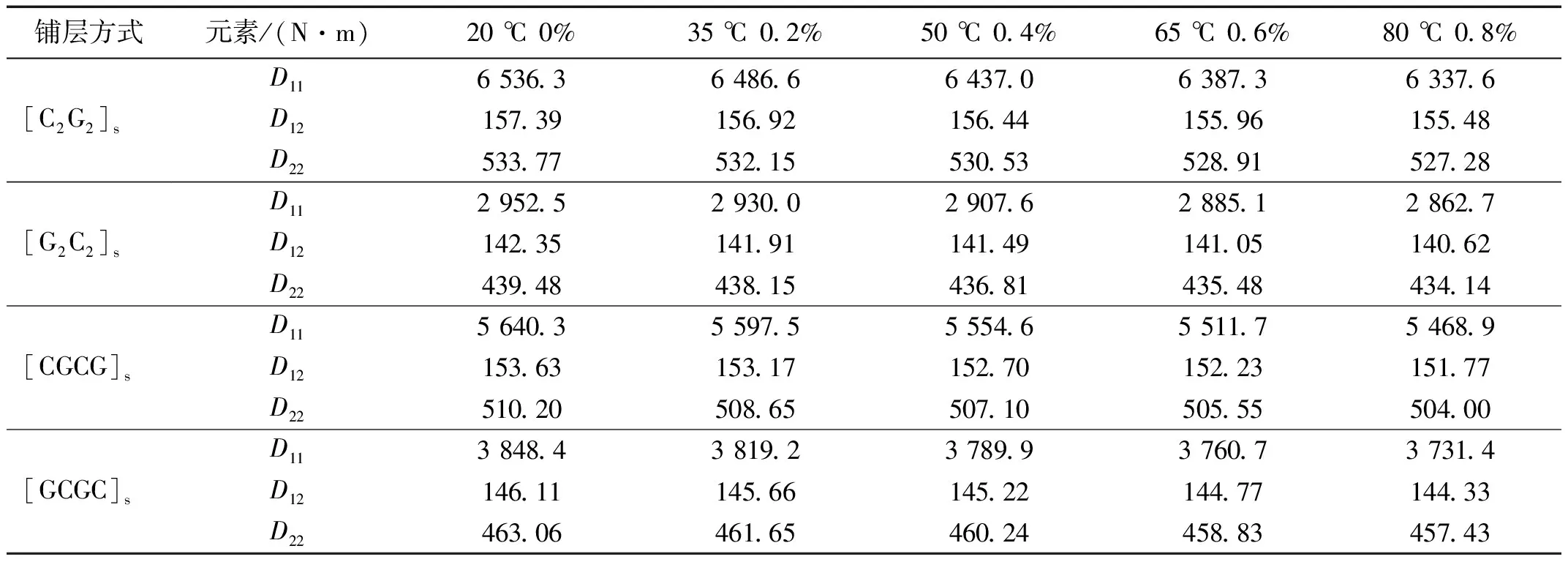
表5 不同湿热环境下层合梁的弯曲刚度D11、D12、D22

由表5可知,温度由20 ℃升高到80 ℃,吸水浓度由0%增大到0.8%,不同铺层方式下的D11、D12、D22变化量基本相同,均分别下降约3.04%、1.21%、1.22%。由此可见,环境湿热因素导致层合梁力学性能下降幅度并不明显,但这并不能直接说明材料力学性能的下降是否是湿热影响材料阻尼特性的机理,还需要进一步研究。

3.1.2 湿热环境对玻/碳纤维混杂复合材料损耗因子的影响

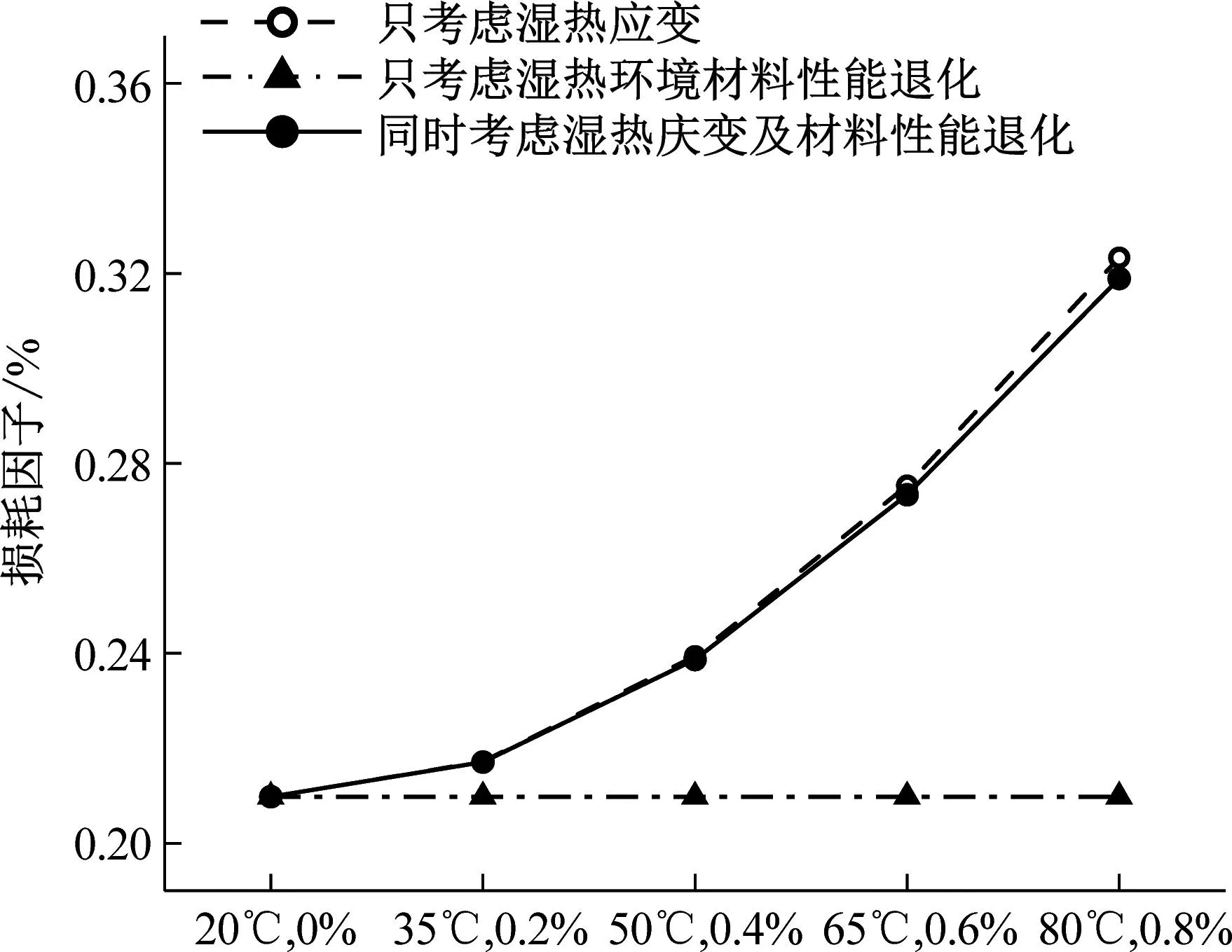
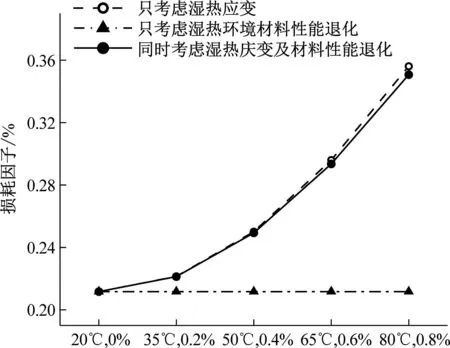
为了进一步研究湿热效应对玻/碳纤维混杂复合材料阻尼特性的影响机理,本节采用控制变量法,分别研究单一因素的影响并比较结果。针对[C2G2]s、[G2C2]s、[CGCG]s、[GCGC]s四种不同铺层方式,在只考虑湿热效应导致层合梁材料性能退化、只考虑湿热应变、同时考虑湿热应变及层合梁材料性能退化三种情况下,分别计算了损耗因子大小,对比结果如图5所示。

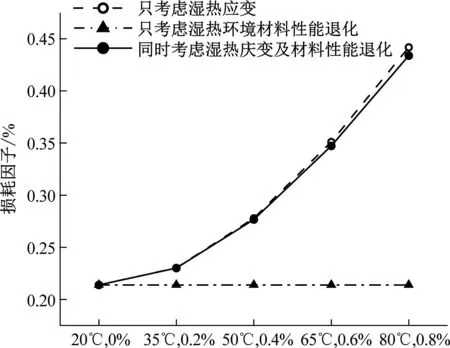
(a) [C2G2]s

(b) [G2C2]s

(c) [CGCG]s

(d) [GCGC]s

由图5可知,随着温度和吸水浓度的增加,各种铺层方式及条件下,材料损耗因子都呈增大趋势。温度由20 ℃增大到80 ℃,吸水浓度由0%增大到0.8%,只考虑湿热应变时,[C2G2]s、[G2C2]s、[CGCG]s、[GCGC]s损耗因子分别增加了106.5%、54.1%、94.3%、68.2%;只考虑材料力学性能退化时,四种铺层方式损耗因子均几乎没有变化,可能的原因是：虽然层合梁力学性能退化,但材料铺层结构不变,有外部激励时储存的应变能U与损耗的应变能ΔU等比例变化,因此两者比值即η无变化。同时考虑湿热应变及材料力学性能退化时,四种铺层方式损耗因子分别增加了102.8%、52%、91.0%、65.7%,此时相较于只考虑湿热应变的情况,损耗因子增量略低,可能的原因是：层合梁刚度降级后,湿热应变导致耗散的应变能减少。

比较三种情况下的损耗因子变化量可知,湿热效应导致材料产生湿热应变是影响材料阻尼特性的主要机理。

3.2 不同条件下湿热环境对玻/碳纤维混杂复合材料层合梁阻尼特性的影响

3.2.1 不同混杂方式下,湿热效应对损耗因子的影响

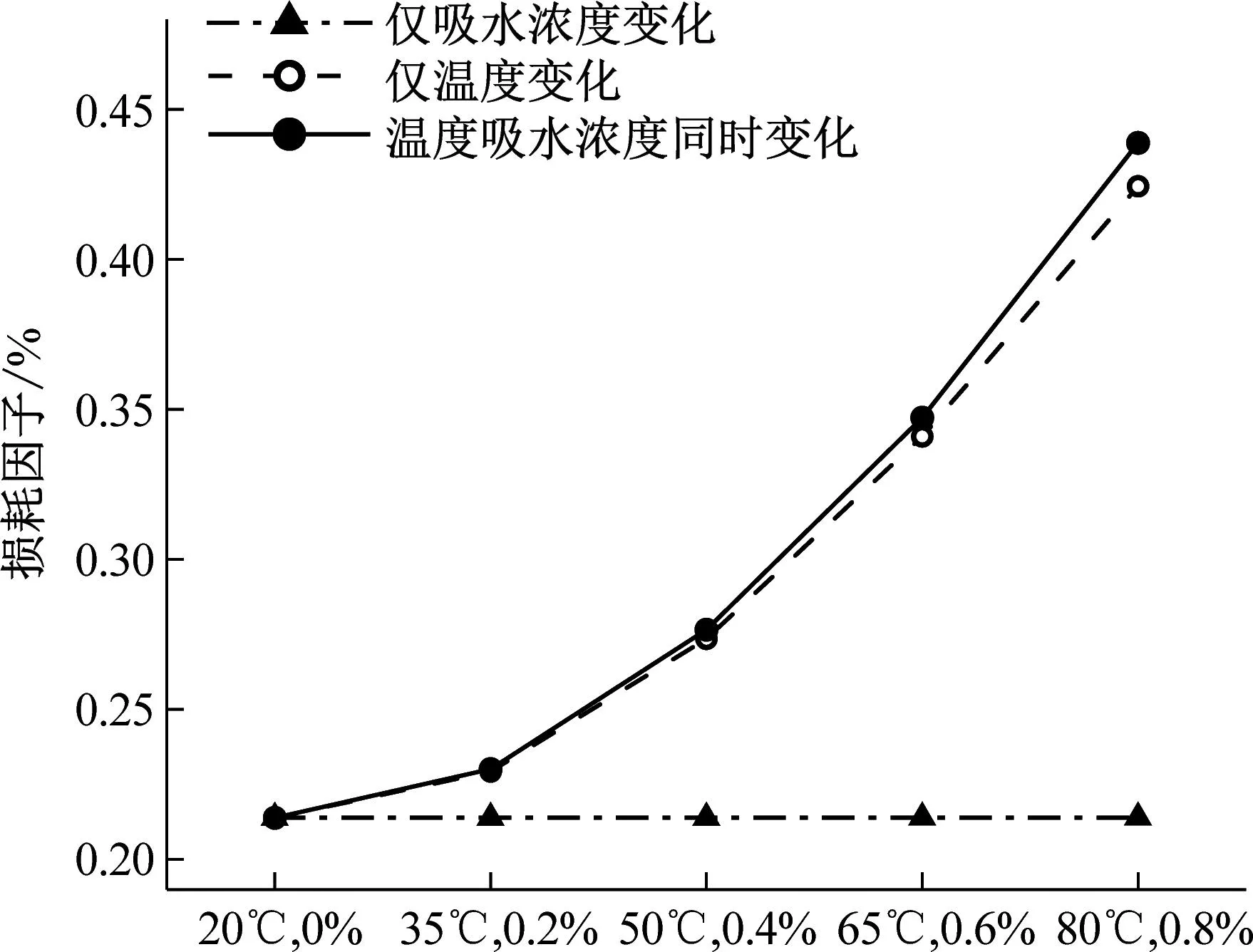
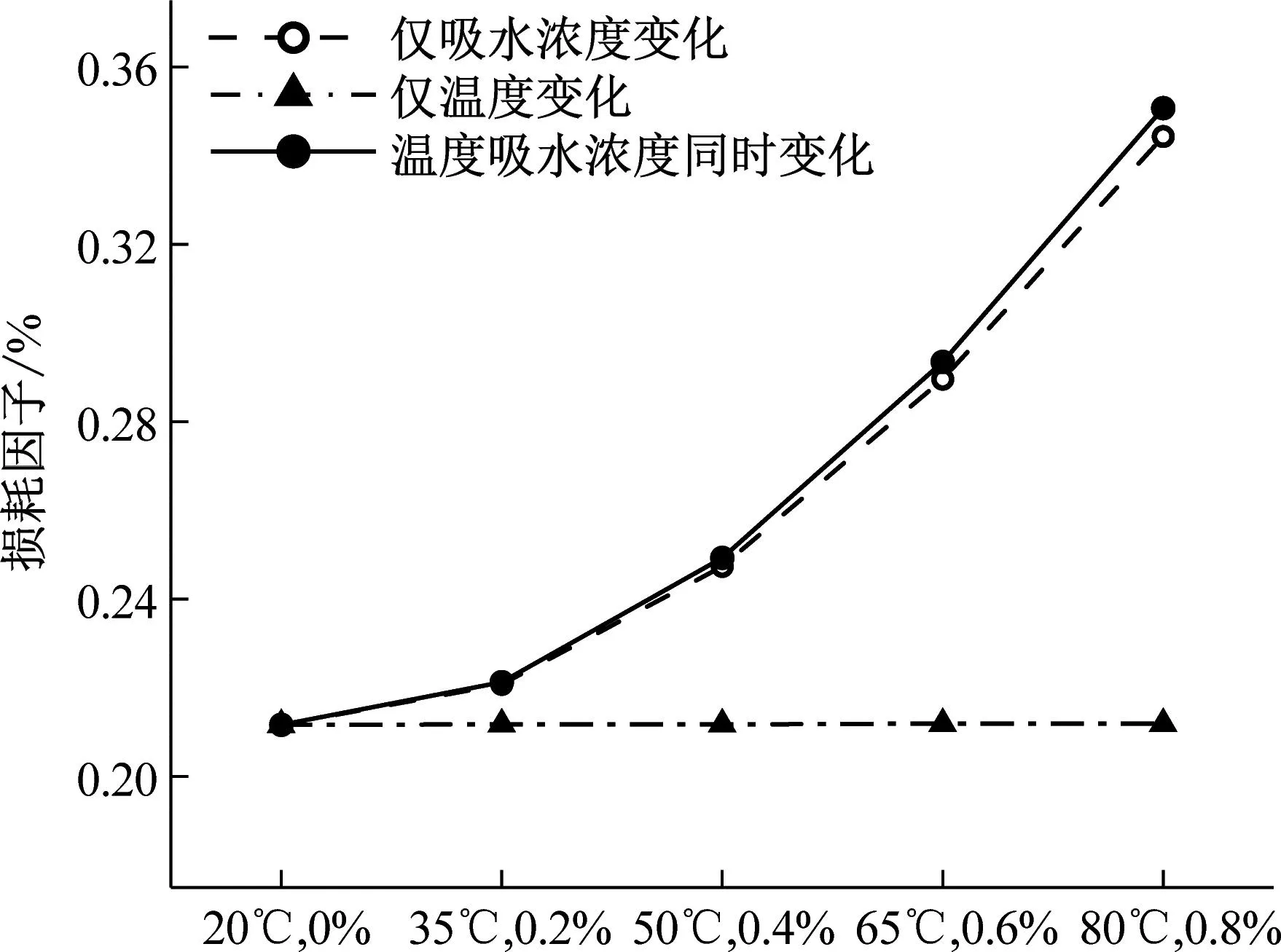
铺层方式对纤维增强复合材料性能至关重要,为研究不同混杂方式下湿热效应对损耗因子的影响,本节分别计算了[C2G2]s、[G2C2]s、[CGCG]s、[GCGC]s四种铺层方式在只考虑温度影响、只考虑湿度影响以及湿热共同影响条件下的损耗因子,结果如图6所示。

由图6可知,温度由20 ℃增大到80 ℃,[C2G2]s、[G2C2]s、[CGCG]s、[GCGC]s损耗因子分别增加了98.4%、49.6%、87.0%、62.6%;吸水浓度由0增大到0.8%,四种铺层方式损耗因子均增加了0.05%左右;湿热共同变化时,四种铺层方式损耗因子分别增加了102.8%、52%、90.9%、65.7%。四种铺层方式下的损耗因子均随温度和吸水浓度的增大而增大,湿热条件等梯度变化时,损耗因子的增幅呈增大趋势。相较于温度影响,湿度对损耗因子影响极小,湿热共同作用时,吸水浓度的影响变大,但还是由温度主导。对比图6(a)～(d)可知,[C2G2]s受湿热的影响最大,[G2C2]s受湿热响最小,[CGCG]s受湿热影响高于[GCGC]s,由此可得碳纤维铺层越集中于外侧时,损耗因子受湿热影响越大。

3.2.2 不同纤维体积分数下,湿热效应对损耗因子的影响

(a) [C2G2]s

(b) [G2C2]s

(c) [CGCG]s

(d) [GCGC]s

纤维体积分数是影响复合材料性能的重要因素,研究不同纤维体积分数下湿热环境对玻/碳纤维混杂复合材料阻尼特性的影响规律对于实际工程应用具有重要意义。在3.2.1节的研究中已知铺层方式为[C2G2]s的层合梁受湿热影响程度最大,故本节以[C2G2]s为研究对象,分别在玻璃纤维体积分数为35%,碳纤维体积分数由35%向65%变化、碳纤维体积分数为35%,玻璃纤维体积分数由35%向65%变化、玻璃纤维和碳纤维体积分数同时由35%向65%变化三种条件下,计算湿热环境下层合梁的损耗因子,结果如图7所示。

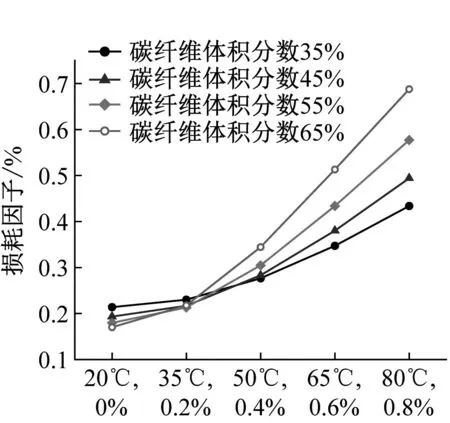
(a) 碳纤维体积分数变化

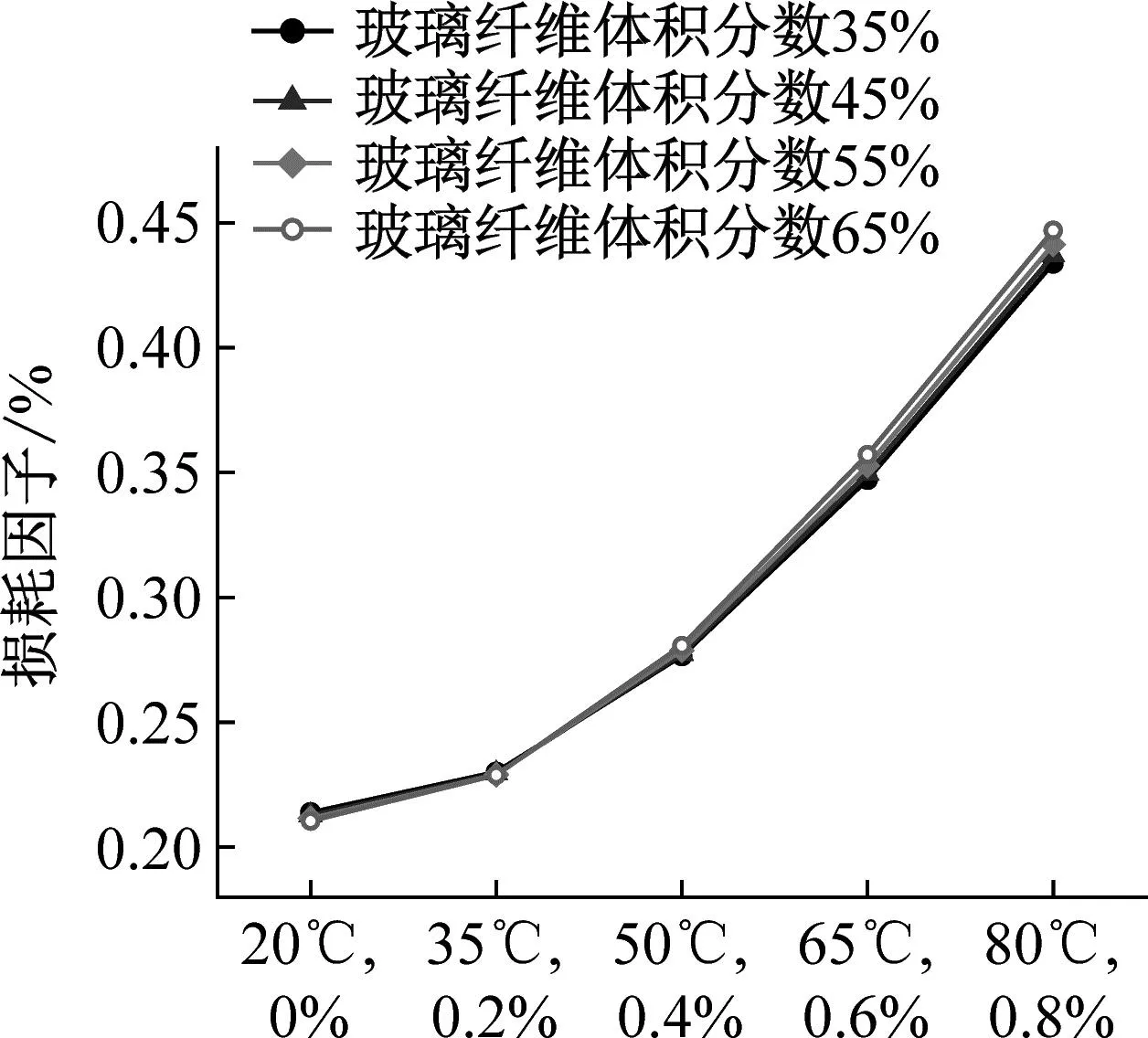
(b) 玻璃纤维体积分数变化

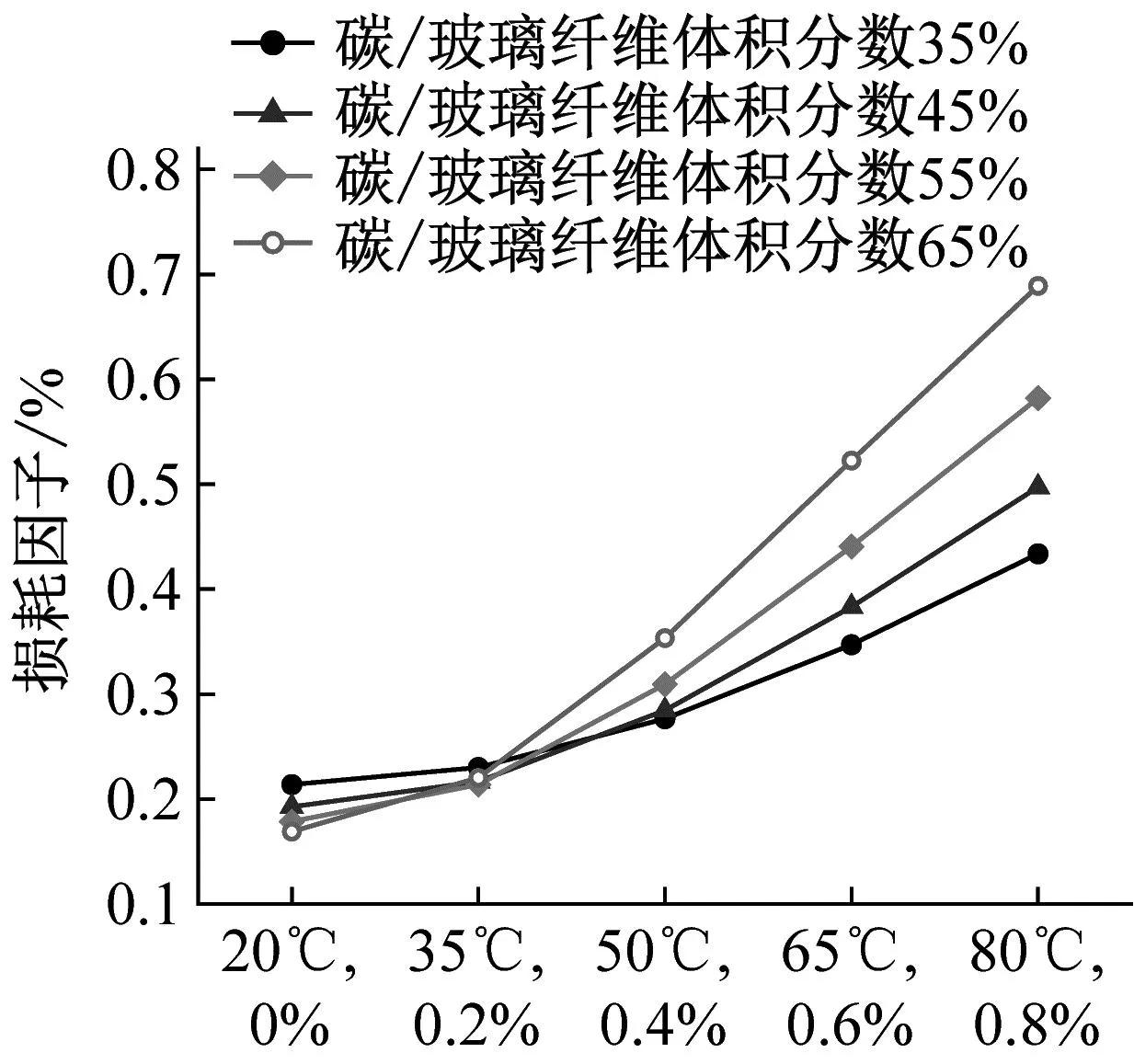
(c) 碳纤维、玻璃纤维体积分数同时变化

由图7可知,不同纤维体积分数下,损耗因子均随温度及吸水浓度的增加而增加。当温度由20 ℃增加到80 ℃,吸水浓度由0%增加到0.8%时,玻璃纤维体积分数为35%,碳纤维体积分数分别为35%、45%、55%、65%的层合梁损耗因子分别增加102.8%、155.6%、221.2%、304.4%。当温度为20 ℃吸水浓度为0时,纤维体积分数越高,损耗因子越低,但随着温度和吸水浓度上升,不同纤维体积分数的损耗因子湿热变化曲线将相交,继续增大温度和吸水浓度,纤维体积分数高的层合梁损耗因子将超过纤维体积分数低的层合梁损耗因子。由此可见,纤维体积分数越高,环境湿热条件变化时损耗因子增量越大,对环境湿热敏感度越高。对比图7(a)～(c)发现,不同玻璃纤维体积分数下的损耗因子湿热变化曲线几乎重合,即对于[C2G2]s混杂复合材料层合梁,玻纤维体积分数造成的影响不大;玻璃纤维碳纤维体积分数同时增加,层合梁损耗因子增量略高于仅碳纤维体积分数增加时的增量。

3.2.3 不同纤维铺设角度下,湿热环境对损耗因子的影响

为研究不同纤维铺设角度下,湿热环境对层合梁损耗因子的影响,本节同样以[C2G2]s为研究对象,分别在玻璃纤维铺层角度为0°,碳纤维铺层角度由0°向90°变化、碳纤维铺层角度为0°,玻璃纤维铺层角度由0°向90°变化、玻璃纤维和碳纤维铺层角度同时由0°向90°变化三种条件下,计算湿热环境下层合梁的损耗因子,结果如图8所示。

(a) 碳纤维铺层角度变化

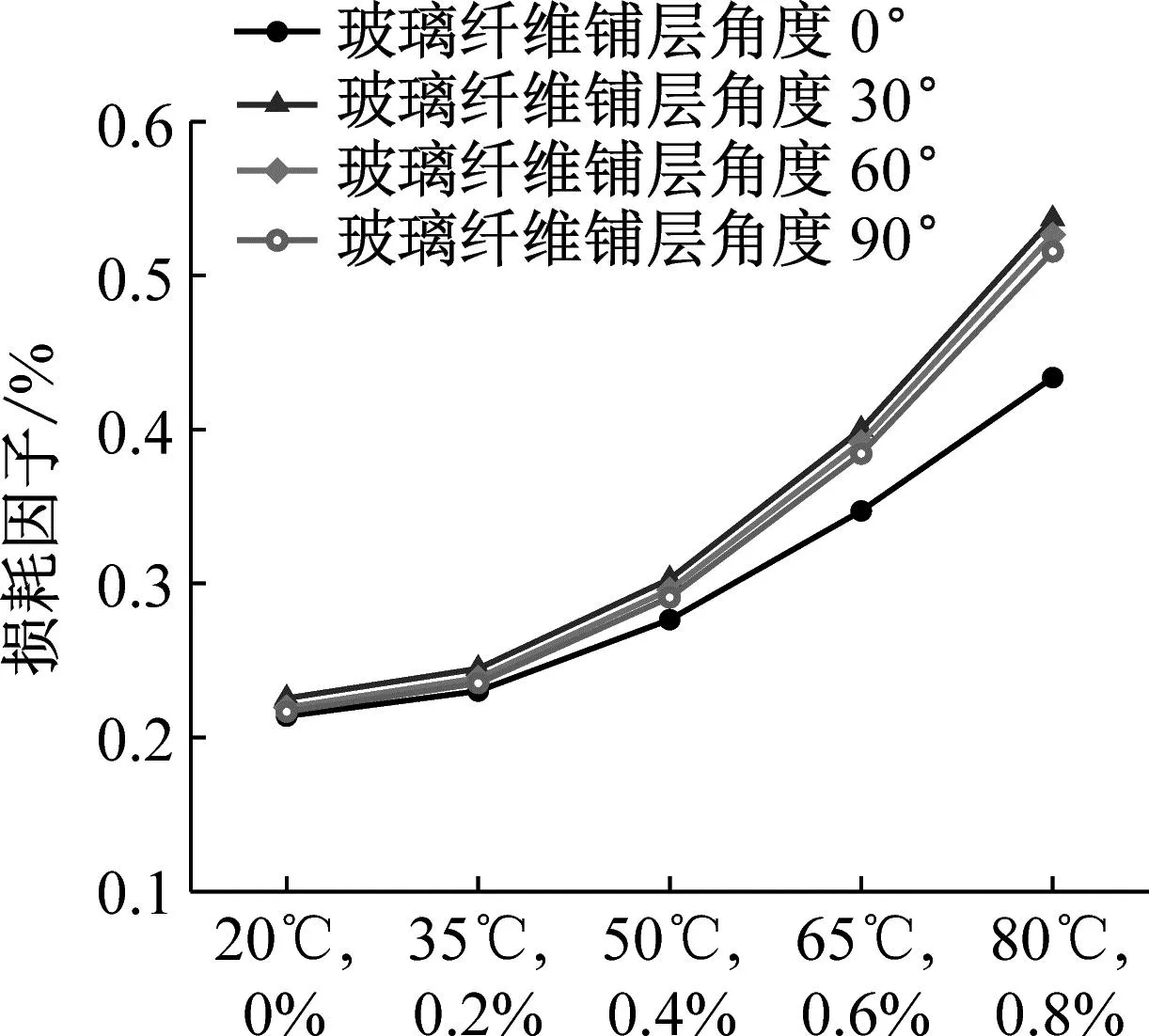
(b) 玻璃纤维铺层角度变化

(c) 碳纤维、玻璃纤维铺层角度同时变化

由图8可知,每一种铺层方式下,损耗因子均随温度及吸水浓度的增加而增加。在损耗因子较低的铺层角度下,湿热对损耗因子影响较大,反之则湿热影响较小。例如图8 (c),玻/碳纤维铺层角度均为0°时,温度和吸水浓度达到最大时损耗因子变化率为102.8%,纤维铺层角度均为90°时,温度和吸水浓度达到最大时损耗因子变化率仅为2.1%。对比图8(a)～(c)发现,对于[C2G2]s混杂复合材料层合梁,玻璃纤维铺层角度发生变化时,对层合梁损耗因子影响较小,碳纤维铺层角度发生变化时,损耗因子变化剧烈,且远高于温度和吸水浓度带来的影响。对比3.2.1及3.2.2发现,纤维铺设角度对损耗因子影响远大于混杂方式及纤维体积分数的影响,是影响损耗因子的首要因素。

4 结 论

本文利用能量耗散原理及宏观应变能法建立了湿热环境下玻/碳纤维混杂复合材料层合梁的阻尼预测模型,并用MATLAB编写了损耗因子计算程序,研究了纤维体积分数、铺设角度、铺层方式、湿热效应对材料损耗因子的影响,主要结论如下：

(1) 温度在0 ℃～80 ℃范围,吸水浓度在0%～0.8%范围,环境对玻/碳混杂复合材料层合梁材料参数影响较小,湿热环境导致材料产生湿热应变是影响阻尼特性的主要机理。

(2) 玻/碳纤维混杂复合材料层合梁各种铺层方式下损耗因子均随温度及吸水浓度的增大而增大,温度的影响远大于吸水浓度的影响,碳纤维铺层集中外侧的铺层方式受湿热影响程度更大。

(3) 不同纤维体积分数的玻/碳纤维混杂复合材料层合梁损耗因子均随温度及吸水浓度的增大而增大。外侧铺层纤维体积分数变化,影响更大。纤维体积分数越高,受湿热影响程度越大。

(4) 不同纤维铺层角度的玻/碳纤维混杂复合材料层合梁损耗因子均随温度及吸水浓度的增大而增大。外侧铺层纤维铺层角度改变,影响更大。在损耗因子较低的铺层角度下,湿热对损耗因子影响较大,反之则湿热影响较小。铺层角度对损耗因子影响远高于湿热、混杂方式、纤维体积分数的影响。

以上结论对玻/碳纤维混杂复合材料在湿热环境下的设计与应用具有一定的指导意义。