非线性动态特性系数对汽轮机转子-轴承-密封系统运动特性的影响

曹丽华, 薛 川, 司和勇, 高路路, 李 想, 郝德成

(东北电力大学 能源与动力工程学院, 吉林 吉林 132012)

密封可以大幅度提高超超临界汽轮机的经济性,但密封腔内也会产生非线性特征明显的汽流激振力影响转子-轴承-密封系统的运动特性与稳定性[1-3]。为更真实的反应转子的运动特性,系统内的非线性动态特性以及转子工作过程中热、动载荷引起的运动特性变化不容忽视。

Alford[4-5]首次发现汽流激振现象,并提出Alford力计算公式,早期的相关研究主要是围绕着Alford力公式分析。为更准确地得到计算模型,研究发现建立密封控制体模型可以提高计算的准确性[6-7]。Muszynska模型虽融入了流体惯性但忽略了其轴向速度,且非线性不强难以计算偏心涡动较大的情况[8-9]。国内学者先后提出摄动算法与振荡流体力学法对转子动力特性的研究提供较大帮助[10-11]。随着数值模拟的发展,模拟精度大幅度提高可以更真实地反映密封腔内流场运动状态。丁学俊等[12]利用静偏心模型考察了转子偏心距、转速对激振力的影响。陈尧兴等[13]利用动网格模型分析了汽轮机非均匀进气对转子动力特性系数的影响。通过理论求解与数值模拟的研究,汽流激振的机理已十分清晰,研究重点已转移到转子动力特性的分析上。曹丽华等[14-15]结合试验法对汽轮机末级叶片模型进行模态分析,得到叶片有无裂纹对转子固有频率以及振型的影响,以及高压缸的运动特性。Kirk等[16-17]利用CFX计算了密封-转子系统泄漏量、压力分布以及密封激振力,并给出了密封齿的结构参数对系统动力特性的影响。司和勇等[18]分析了汽轮机工作状态中高温密封齿膨胀变形和直接刚度与阻尼的变化对转子运动特性的影响。Cangioli等[19]建立了一种新的迷宫式密封的热弹性体流模型,并分析了高温下边界压力、转速、进口预旋比等对转子运力特性和稳定性的影响。在转子-轴承系统的研究中为让模拟更接近实际情况,部分学者提出单纯线性理论的考察有一定局限性和考虑非线性因素是十分必要的并推导了包含非线性因素的动力学方程[20-22]。Elliott等[23]分析了非线性阻尼系统讨论了计算方法以及实际例子。Hou等[24]利用多尺度方法归纳飞机旋翼系统非线性特征得到并求解运动方程分析了其运动特性。Iskakov等[25]利用线性阻尼与非线性阻尼综合表达系统中的总阻尼,分析了其对系统稳定性的影响。Sayed等[26]尝试利用二阶微扰方确定轴承非线性刚度、阻尼系数并确定其有效范围。Civera等[27]利用具有非线性刚度和阻尼项的解析SDoF模型,计算了高度灵活机翼的大振荡,并讨论了其在频域中的稳态响应。Amer等[28]研究了具有三自由度的运动系统中非线性阻尼对其稳定性的影响。目前针对汽轮机转子-轴承-密封系统的运动特性的研究基本上都基于线性理论分析,在转子涡动过程中仅用线性刚度、阻尼来表达转子的弹性恢复力,为更真实的反应转子的运动状态,转子的非线性动态特性不能忽略。

为准确地考察超超临界汽轮机转子-轴承-密封系统的运动特性,本文充分考虑了系统中非线性动态特性以及热、动载荷对其的影响,推导了不同条件下的转子运动微分方程并通过试验验证了其准确性。在此基础上建立转子-轴承-密封系统Jeffcott模型,将高精度数值模拟求得的汽流激振力,建立密封激振力的拟合公式,将其耦合到转子运动方程中。利用龙格-库塔法求解对应的运动方程,分析不同条件下转子的运动特性与稳定性。为抑制汽流激振、提高汽轮机的运行稳定性提供可靠理论依据。

1 数学模型

1.1 物理模型

根据某超超临界汽轮机高压缸第二压力级设计参数,建立1.5级转子-轴承-密封全周物理模型,如图1所示,考察静叶、叶顶、动叶运行过程中产生的激振力。模型具体结构参数如表1所示。工作条件如表2所示。采用曹丽华等的动网格计算方法建立涡动模型,将动静间设为变形面,使密封与叶片流域相通,可准确反应出密封内部流动,有效的解决数值仿真中的网格变形问题。根据不同负荷下的蒸汽参数来设置计算时对应的边界条件,可获得8组不同偏心量,每组12个不同频率的汽流激振力,将其按直角坐标系分解,其中x方向的激振力如图2所示。

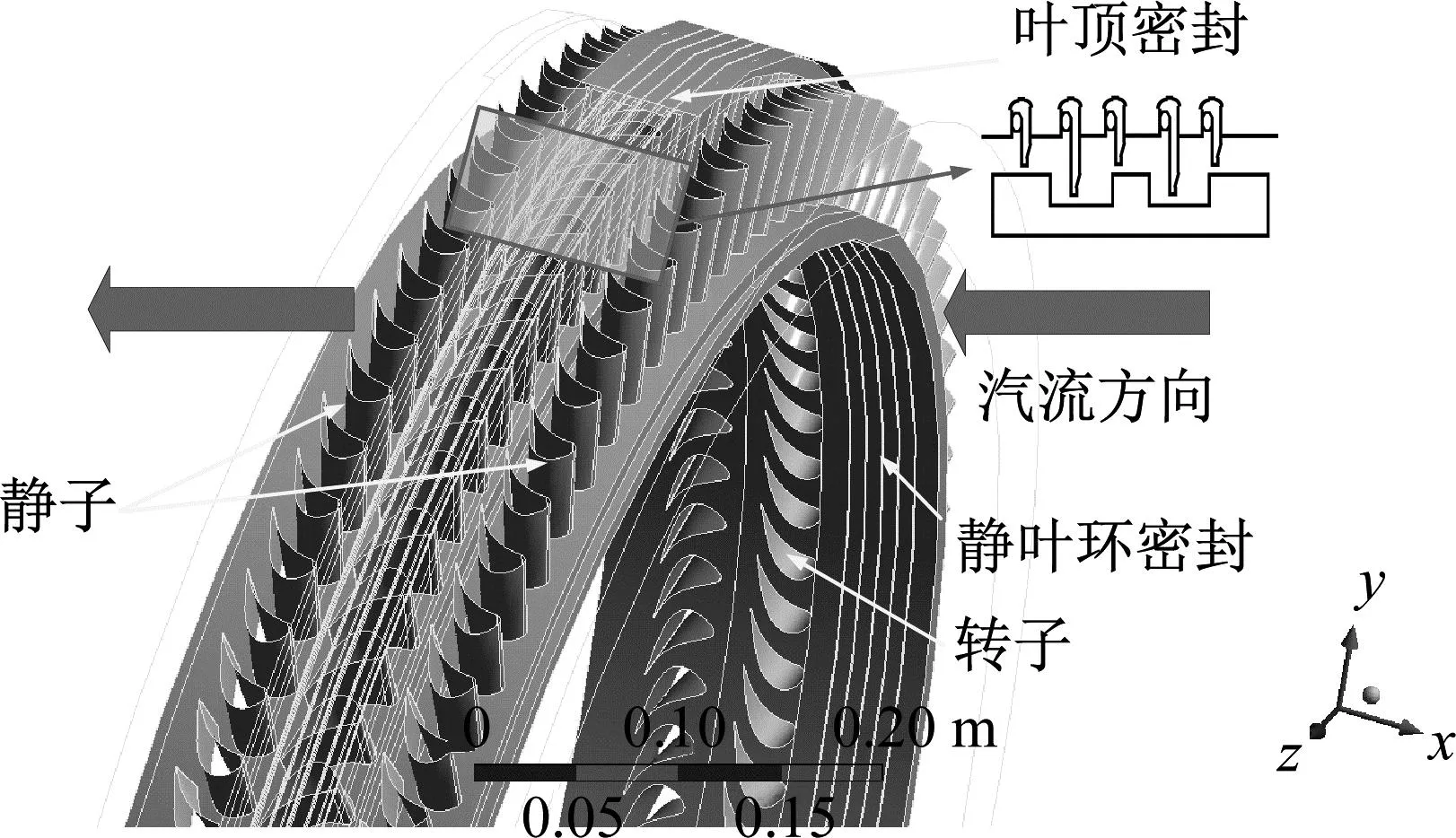
图1 1.5级物理模型

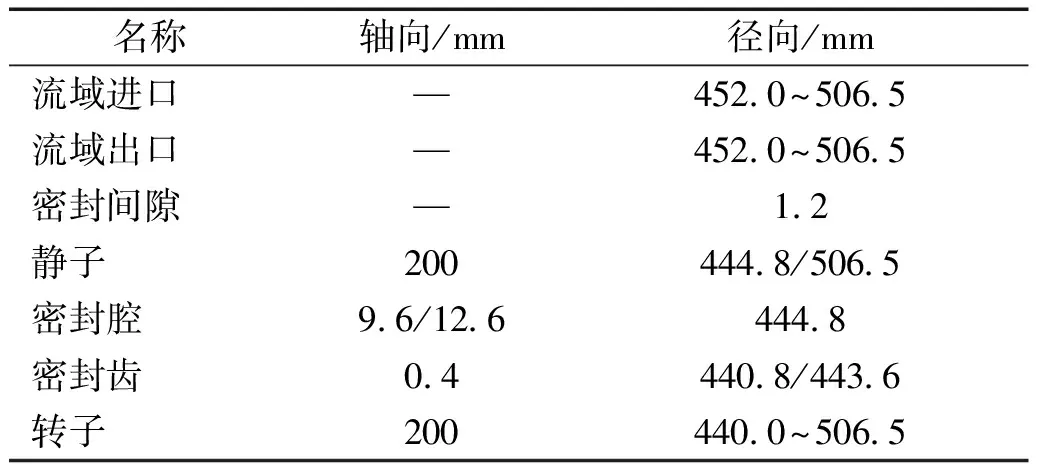
表1 结构参数

表2 计算模型的工作条件

1.2 油膜力模型

利用Capone短轴承油膜力模型[29],获得x、y方向的非线性油膜力。短轴承是指长径比较小的轴承,采用此模型是由于其具有良好的计算精度与收敛性,通过改进长径比可以获得更加适用于超临界汽轮机的轴承特性。

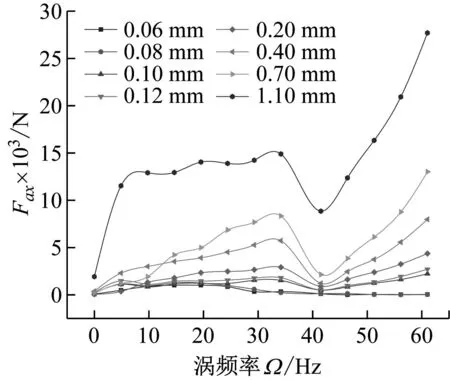
图2 x方向不同偏心量下的激振力

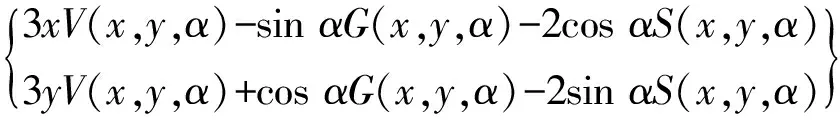
(1)

其中：

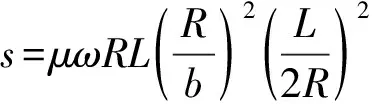
1.3 激振力模型与运动微分方程

通过Fluent和动网格技术所获得的不同偏心量激振力具有十分明显的非线性特征难以用现有公式描述,将其进行多频涡动计算,利用MATLAB幂次拟合多项式的方法表达激振力函数,如式(2),可准确的描述任何频率与偏心量变化的非线性汽流激振力,其具体计算公式如式(3)。图3为x方向激振力MATLAB拟合函数图。

Fax=f(Ω,Cr)

Fay=f(Ω,Cr)

(2)

Fax=3 212+2 846Cr-1 384f-1 718Cr2-511Crf-
721.8f2+68.94Cr3+199.8Cr2f-934.1Crf2+
1 818f3+775.4Cr4+139.6Cr3f+52.13Cr2f2+
1 014Crf3+321.3f4-134.2Cr5-72.18Cr4f+
60Cr3f2-45.59Cr2f3+385.2Crf4-210.4f5

Fay=3 381+1 895Cr+85.31f-3 170Cr2+1 471Crf-
1 634f2+2 011Cr3-214.6Cr2f-1 667Crf2+
845.9f3+2 366Cr4-1 199Cr3f+368.3Cr2f2+
514.7Crf3+720.9f4-1 170Cr5+546.5Cr4f+
35.13Cr3f2-187.5Cr2f3+848.4Crf4-62.01f5

(3)

式中：Fax、Fay分别为x,y方向的非线性汽流激振力;Cr为偏心量;f为涡动频率。

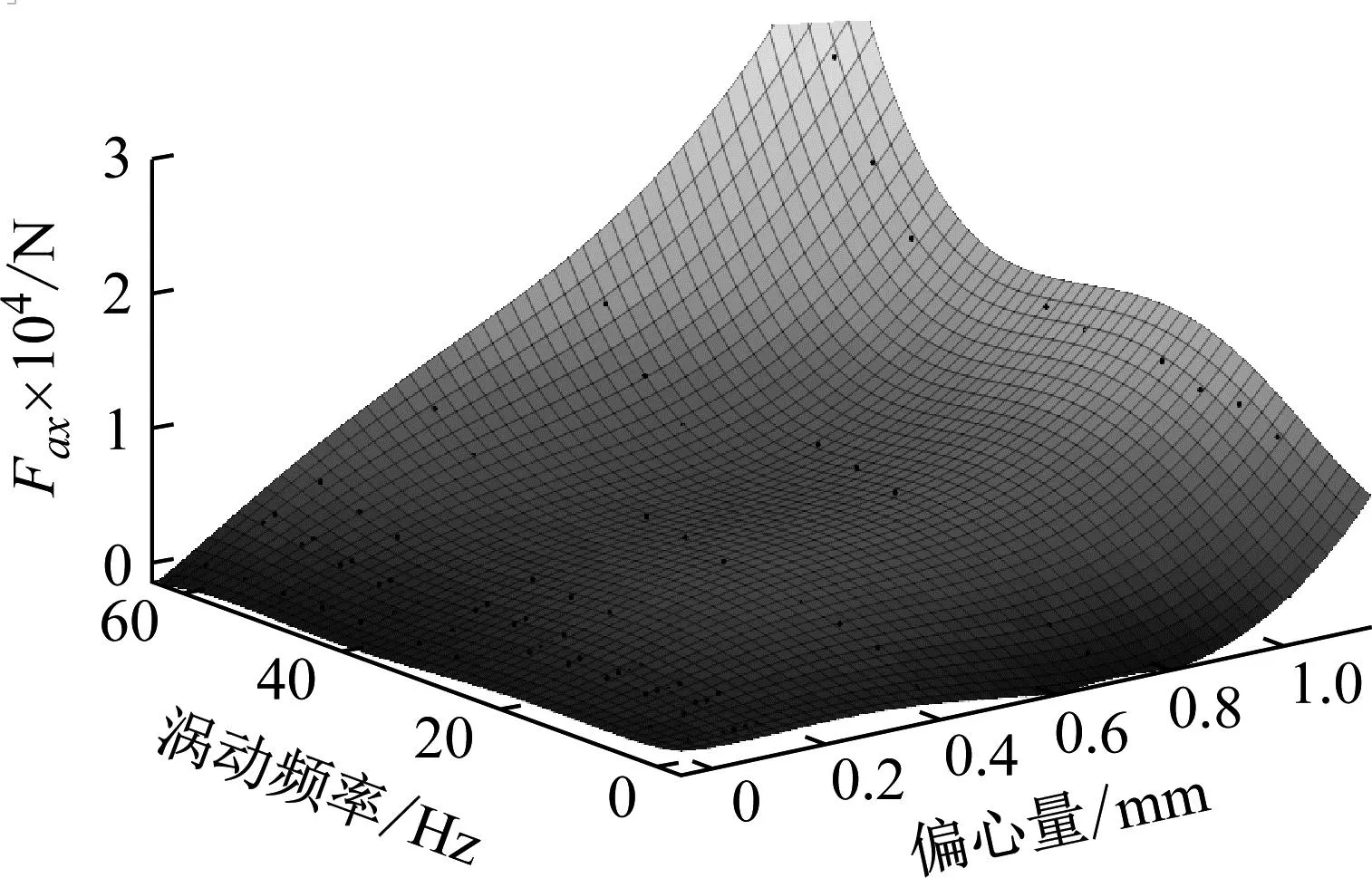
图3 x方向不同偏心量下激振力拟合函数图

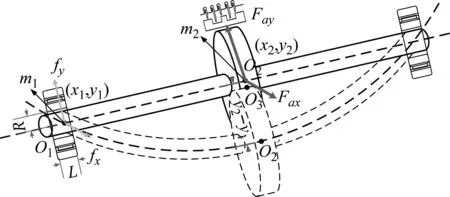
图4 Jeffcott模型示意图

具有一般线性单自由度机械系统的运动微分方程为

(4)

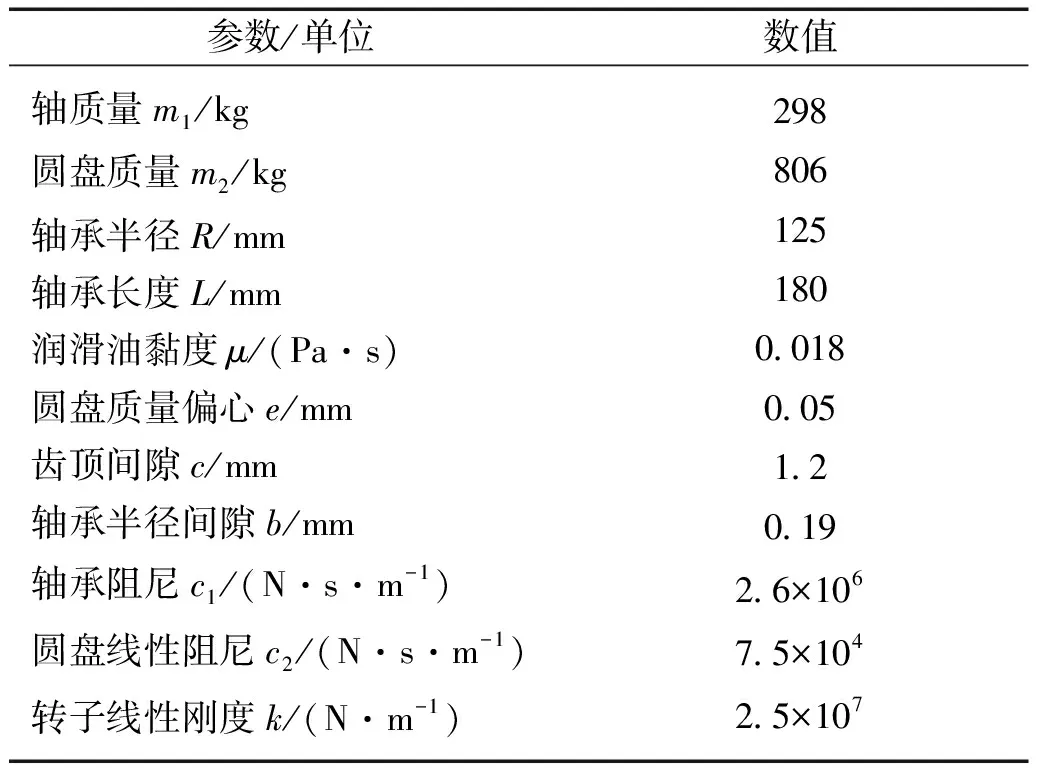
表3 系统模型的主要参数

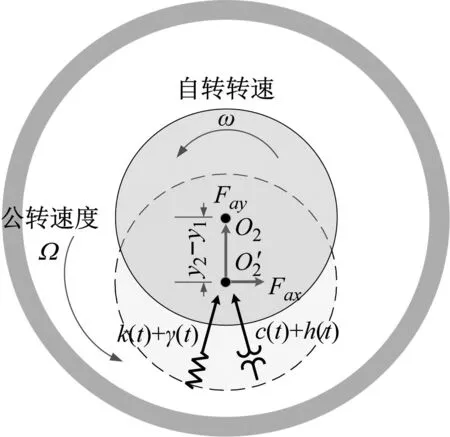
图5 转子转动示意图

式中：m为系统集中质量;c、k分别为系统线性阻尼、刚度系数。

将其扩展到转子-轴承-密封系统可得

(5)

为使方程能更准确地反映转子的运动状态,分析中刚度、阻尼都用线性项和非线性项来综合表达。首先只考虑系统非线性刚度式(4)转化为

(6)

式中,γ为系统的非线性刚度系数,且与转子位移的立方成正比。分析中将非线性刚度跟随转子位移分解成在x、y方向的分量。

此时系统的运动微分方程为

(7)

当只考虑系统非线性阻尼时,式(4)转化为

(8)

此时非线性阻尼与转子速度的n次幂成正比,为体现转子移动速度的方向则有

(9)

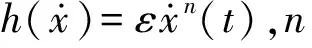
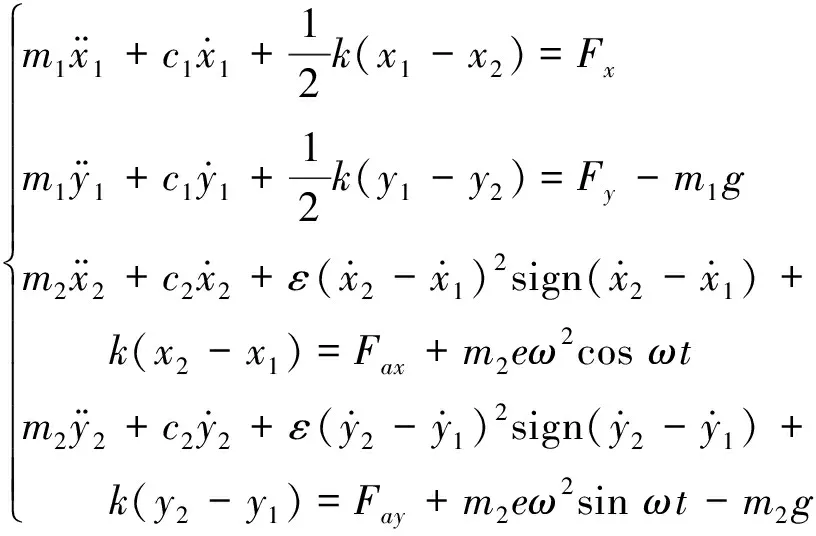
(10)

同时考虑系统内非线性刚度、阻尼时,式(4)转化为

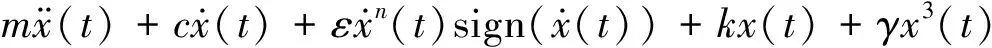
(11)

运动微分方程为

(12)

1.4 试验验证

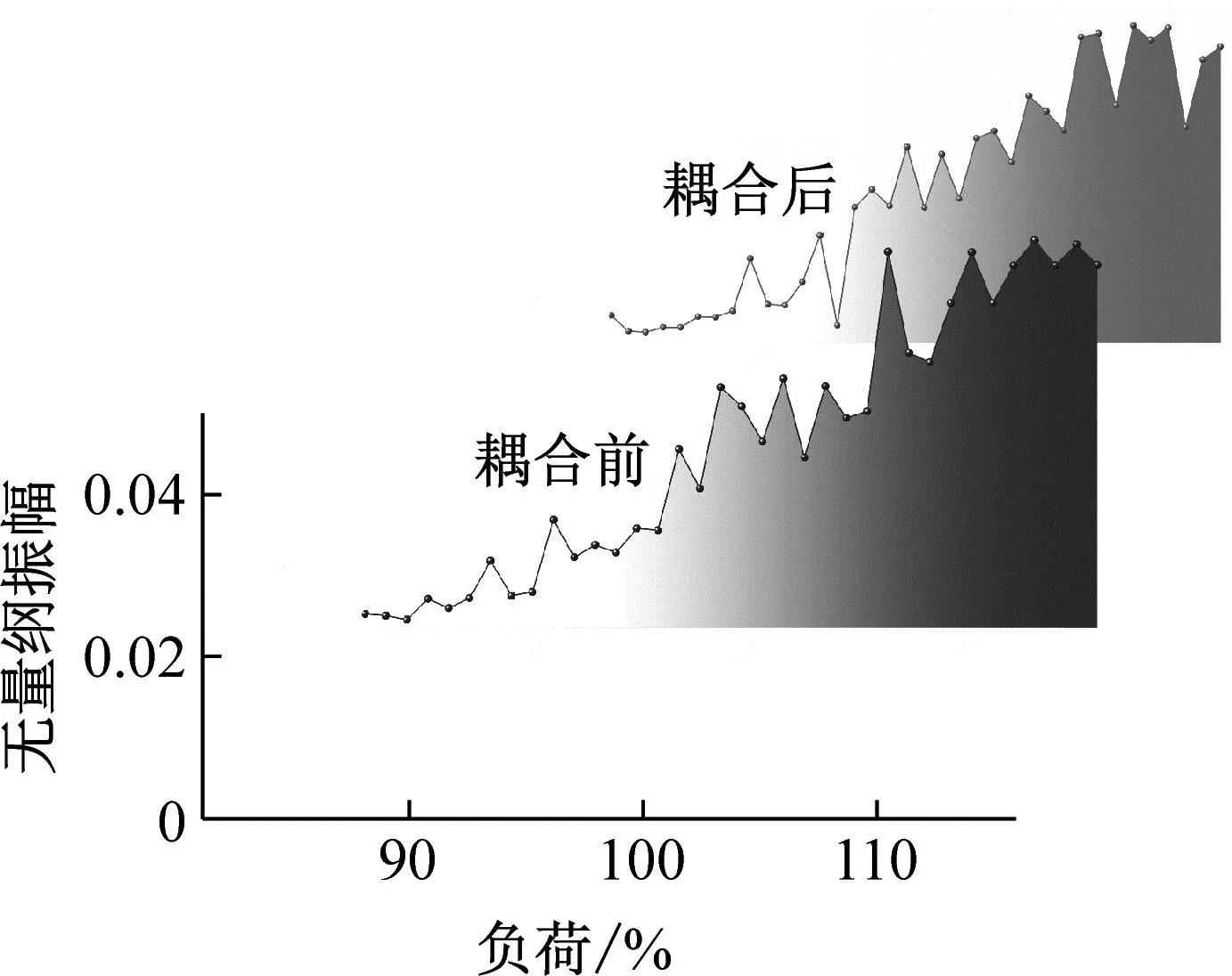
现有的研究已发现工程实际中转子内的非线性动态特性对其运动特性有明显影响但并没有与激振力耦合研究。为验证激振力模型及包含非线性动态特性的运动方程的准确性,基于如图6的转子-轴承-密封试验台进行验证,其具体参数如表4所示。试验台通过调整转子平台高度来控制齿顶间隙,使其在0.5～3 mm范围内可调,并通过多次试验测量对其进行修正,确保误差低于5%。通过调控风量来控制转子转速,使其稳定增加到316 rad/s,合理布置电涡流键相传感器,采集转子的位移信息,考察转子不同转速的涡动幅值。图7、8分别为不同转速的振幅曲线和额定转速频谱图,展示了不考虑非线性动态特性,考虑非线性动态特性与试验值的对比,其中不考虑的由式(5)模拟获得,考虑的由式(12)模拟获得。图7中可以看出考虑非线性动态特性系数的幅值曲线更接近试验值,特别是在汽轮机额定转速附近更为明显。图8也可看出额定转速下考虑非线性动态特性系数的频谱图与试验值更为接近。说明本次研究模型设计合理、运动方程正确,也说明考虑系统内非线性动态特性能够更准确的反应转子的运动特性。

图6 转子-轴承-密封试验台

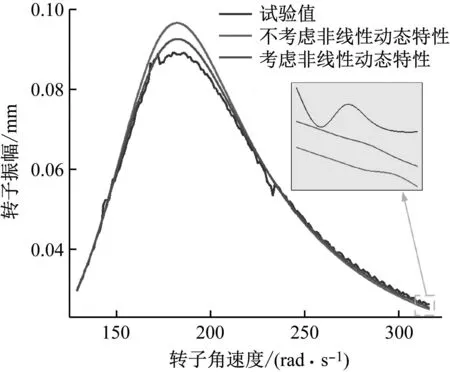
图7 转子振幅

2 计算结果分析

为深度揭示非线性动态特性系数对系统运动特性的影响,把非线性刚度、阻尼及其耦合效果分别进行分析。利用龙格-库塔法求解,可得不同条件下转子涡动状态。计算过程中每完成一步,流场随之更新,通过不断迭代计算,考察不同条件下系统的运动特性。

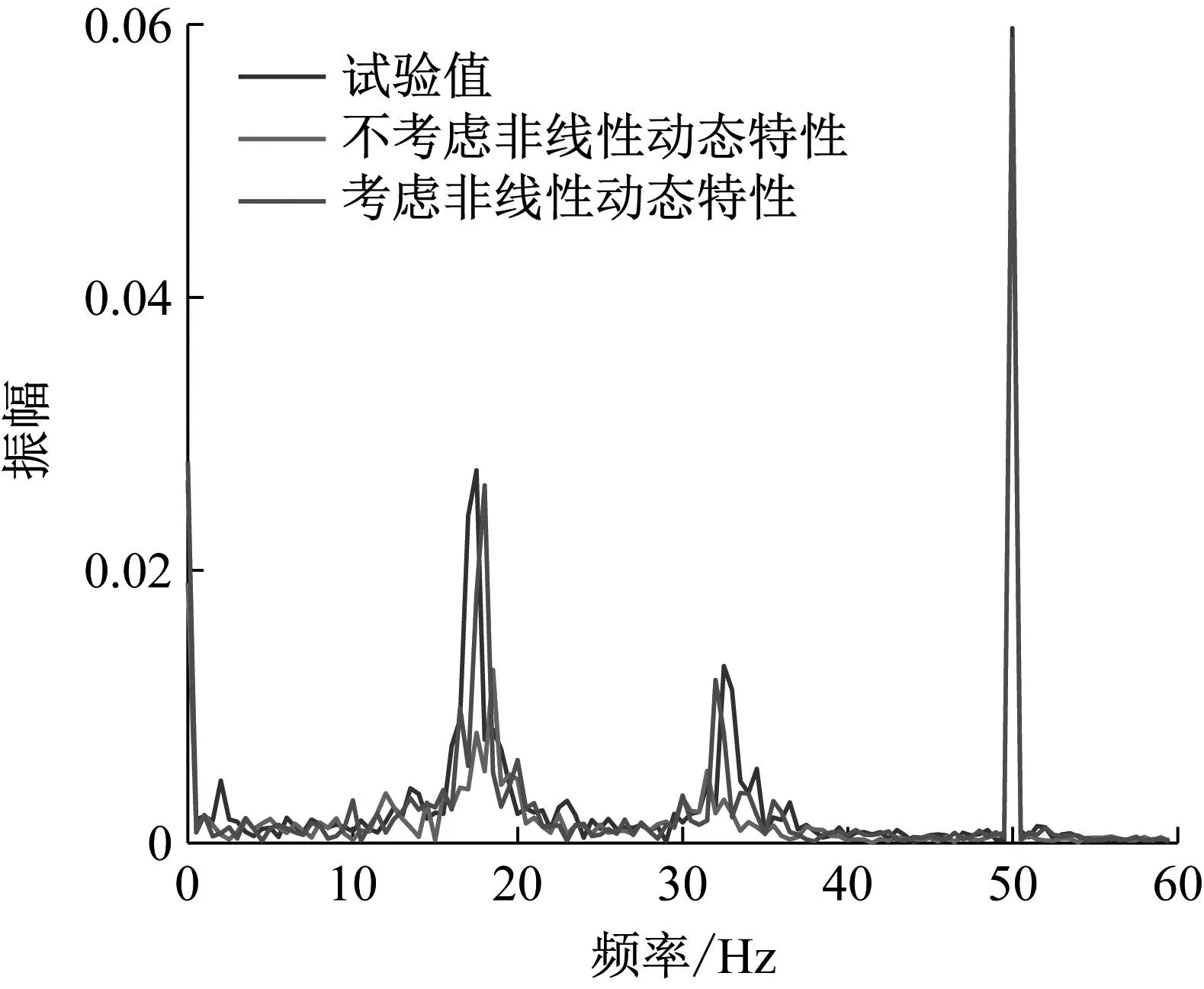
图8 额定转速频谱图

表4 试验台的主要参数

2.1 非线性刚度对系统运动特性的影响

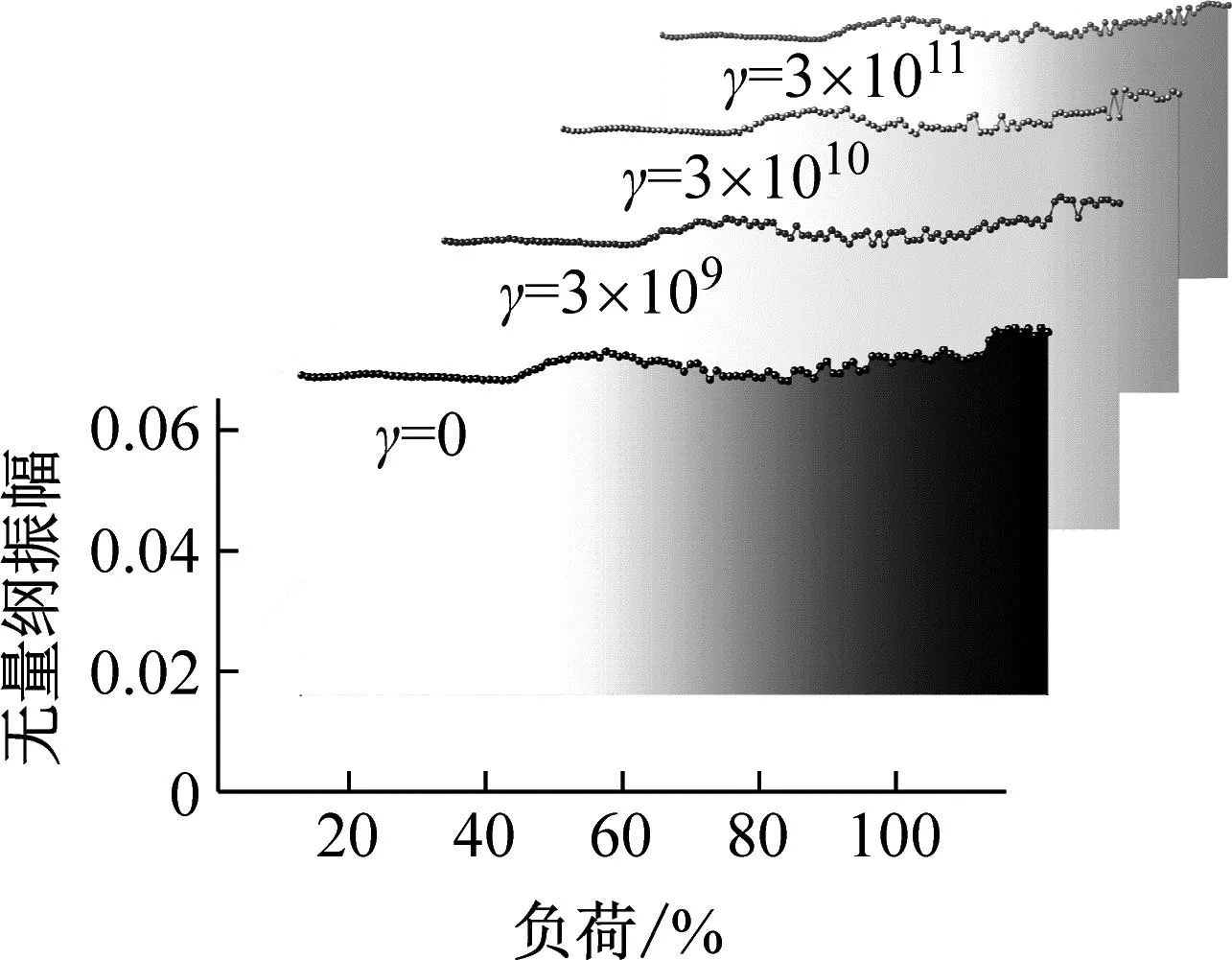
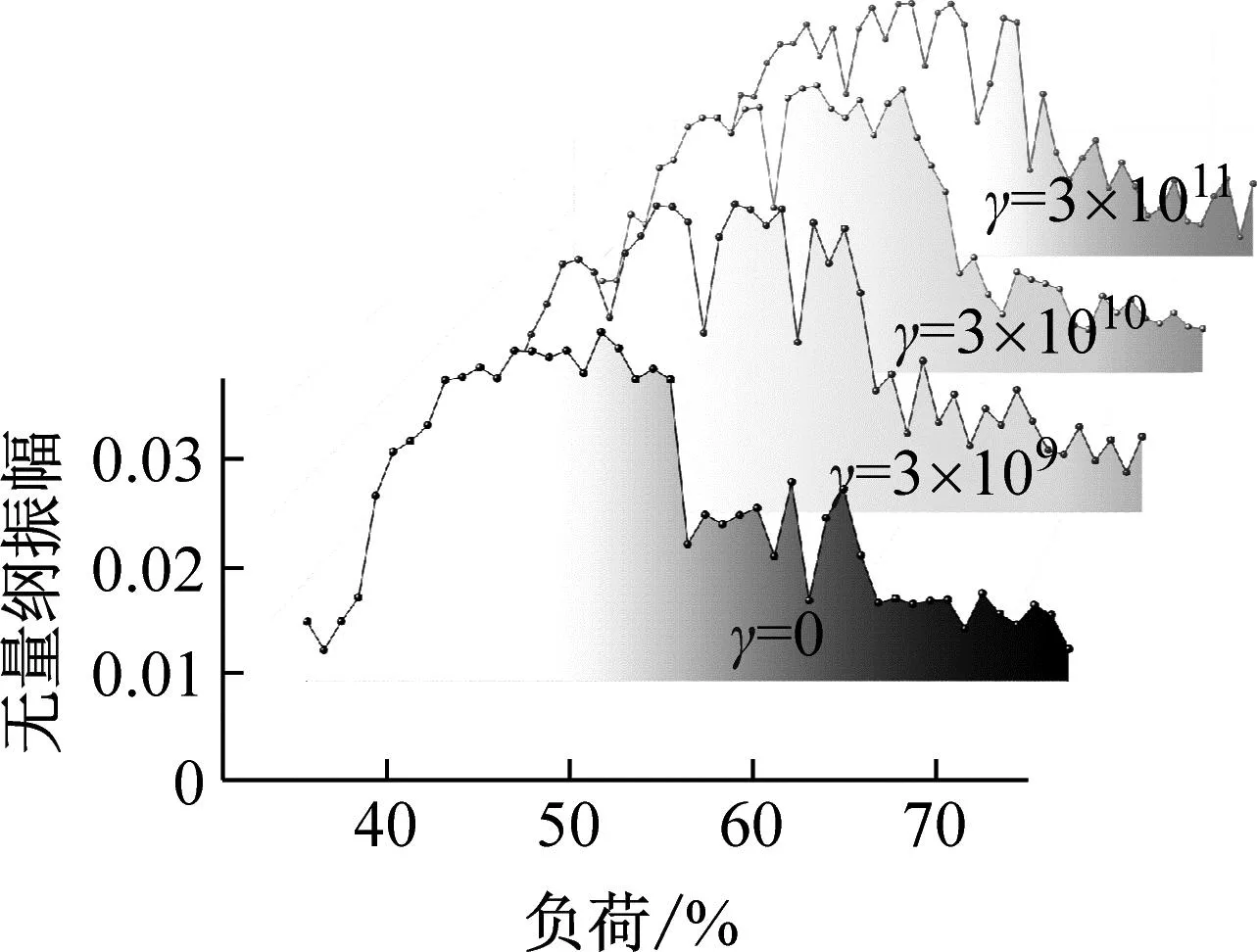
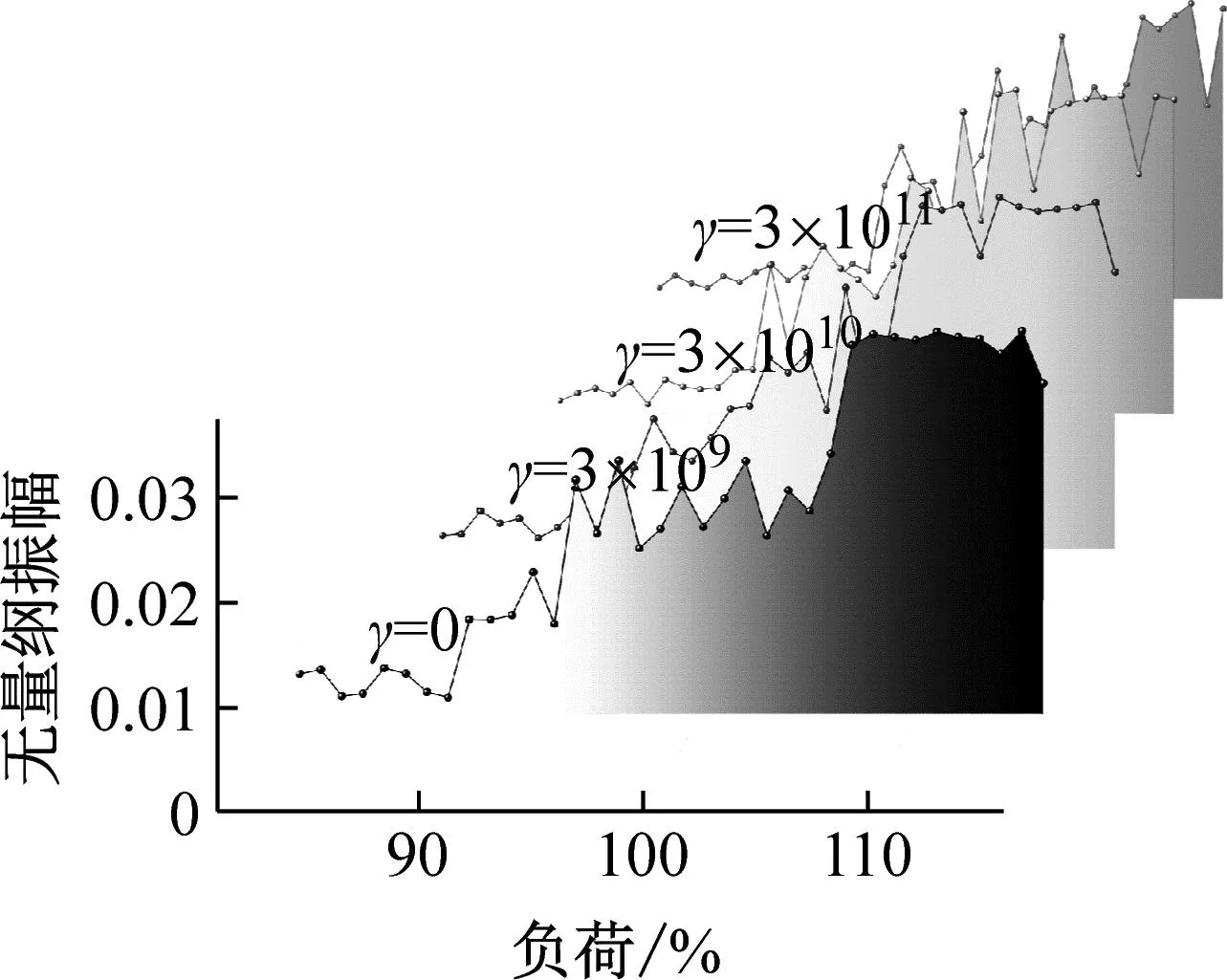
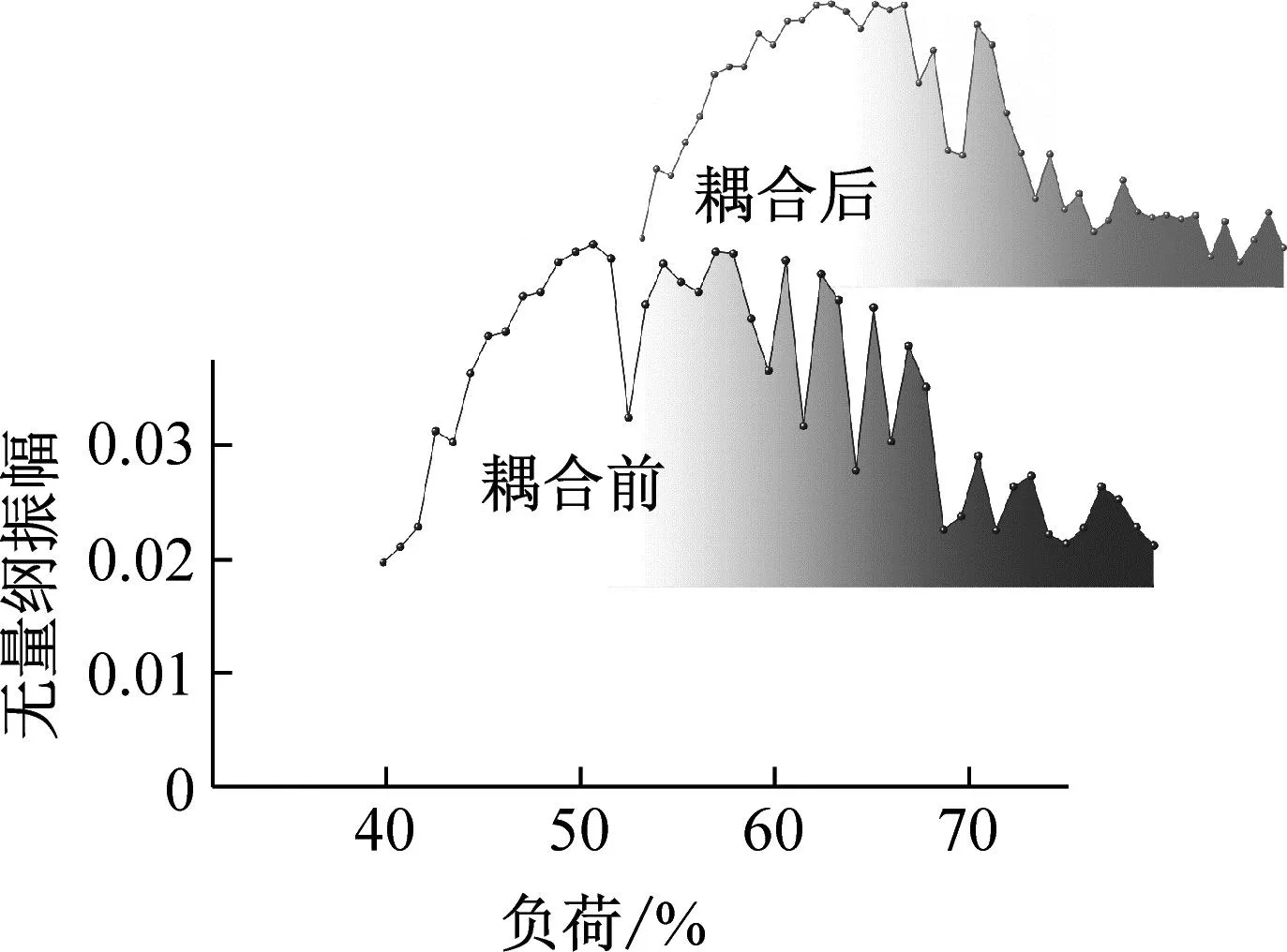
图9为不同非线性刚度转子系统分岔图,直观来讲随着负荷的增加转子的运动都经历了类似混沌二周期-类似混沌一周期-类似混沌二周期-具有分散性的混沌周期四种变化。开始的类似混沌二周期在1%～5%THA(turbine heat acceptance)左右,这是由于系统初带负荷,突然的载荷使转子发生扰动,之后转子位移变小进入类似混沌一周期,直到33%THA左右混沌一周期开始向混沌二周期转变,经过短暂的过渡,分岔图主要集中在上下两部分。负荷达到58%THA后转子进入复杂的混沌运动,当系统进入VWO(valve whole open)工况后有向混沌三周期转化趋势。观察非线性刚度介入后的变化,非线性刚度对负荷较低的情况影响不大,系统进入混沌二周期时,当γ=3×109N/m3、γ=3×1010N/m3时分岔过程稍加柔和,特别是后者分岔过程柔和且分布集中,而γ=3×1011N/m3时此区域变得零散,混沌特征明显。对比负荷高于55%THA后的情况,考虑非线性刚度后转子运动更加集中、位移减小,其中γ=3×1010N/m3时最为明显。当系统达到VWO工况后非线性刚度会使转子运动转向混沌三周期趋势更加明显。总体来看一定范围内的γ值可减小转子位移量。

图9 不同γ值分岔图

将转子的无量纲位移进行快速傅里叶变换,可得到不同非线性刚度转子系统频率瀑布图,如图10所示。展示了激振力与油膜力对系统升负荷过程中造成的分频现象。总体上看在6%THA之前系统都有幅值较小的1/2工频,随着负荷的增加逐渐消失,这是由于系统初带负荷产生的。28%THA左右1/2工频又再次出现且幅值较高,60%THA后,1/2工频逐步分化成1/3、2/3工频。在分化出现后密频效果愈发明显,这是由于负荷越高,密封腔流场越复杂,汽流激振力非线性特征越明显,多频涡动中的其它频率振动开始展现。对比发现耦合非线性刚度后密频现象更为明显,尤其在60%～70%THA时。考察四种情况整个分化部分密频现象的增加情况,其中γ=3×1010N/m3时密频现象较少。

图10 不同γ值瀑布图

图11为不同非线性刚度的主要频率无量纲振幅图,展示了系统的主要频率分布。本次研究中不仅考察汽流激振力对转子系统的影响还包含油膜力,随着系统负荷的增高,激振力逐步加大与油膜力产生耦合作用,引起以1/2工频为主的振动,随着激振力进一步增大,1/2工频开始向1/3、2/3工频演化,其中1/3工频主要由激振力作用产生,2/3工频主要由油膜力作用产生,而且由于高负荷时汽流激振力更大作用更明显,因此1/3工频幅值更高。如图考虑非线性刚度后对工频基本没有影响,但对其它主要频率有一定影响。随着γ取值的增高1/2工频位置稍向高负荷方向移动,且区域略有增加,1/3、2/3工频区域幅值略有降低。这是说明非线性刚度延缓了激振力与油膜力的作用效果。且在主要频率高幅值集中区都有低幅值出现,这也对应了图10耦合非线性刚度后密频现象明显。说明非线性刚度减小了激振力与油膜力的作用效果,但导致多频涡动中的其它频率振动增多。

2.2 非线性阻尼对系统运动特性的影响

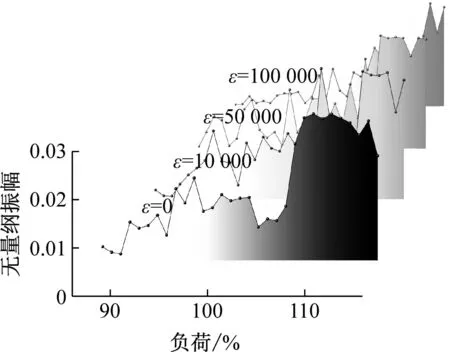
图12为不同非线性阻尼转子系统分岔图,非线性阻尼对转子位移的整体运动趋势没有改变,但使系统由混沌一周期进入混沌二周期的分岔过程变得柔和,在混沌二周期阶段非线性阻尼介入后此区域范围明显变大,并随着ε值的增加逐步减小。系统进入复杂混沌运动后ε值越高转子位移越小。当系统达到VWO工况后转子转向类似混沌三周期趋势减弱。

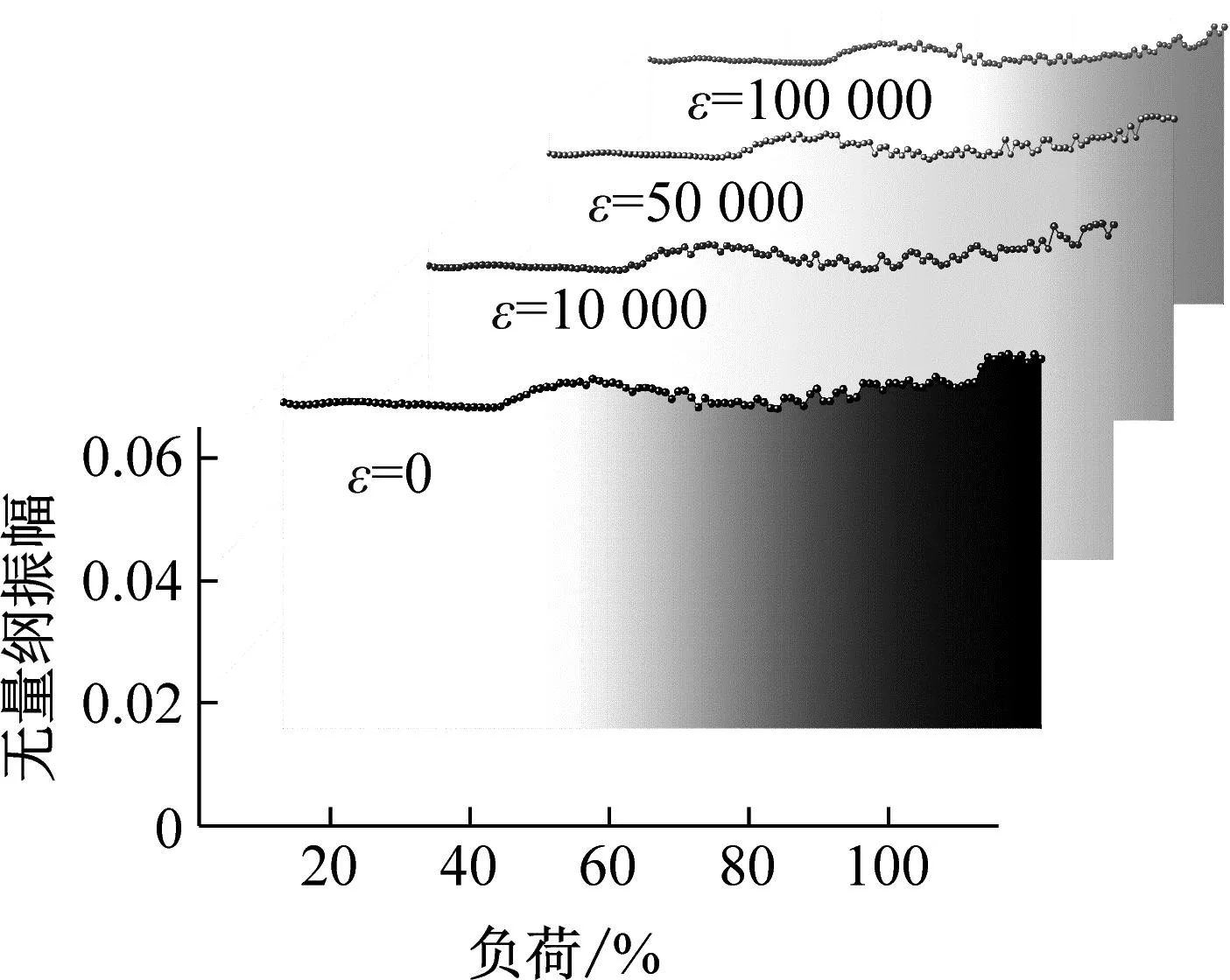
图13为不同非线性阻尼转子系统频率瀑布图,图中四种情况在负荷达到30%THA后都出现了相似的密频现象,且考虑非线性阻尼后更明显。在系统由1/2工频向1/3、2/3工频演化初期集中的密频现象随着ε值的升高而减弱,且整个演化过程的密频振幅也随ε值的升高减小。

图14为不同非线性阻尼的主要频率无量纲振幅图,由图14(b)可知,1/2工频随着ε值的增加有向高负荷方向的移动,且幅值略有降低,区域有所增加。说明在负荷较低时非线性阻尼的增加使系统产生1/2工频需要更大的耦合力(激振力与油膜力),且需要更大的激振力开始向1/3、2/3工频演化。由图14(b)、(c)可知,随着ε值的增加1/3、2/3工频区域明显减少,且幅值降低。

(a) 工频

(b) 1/2工频

(c) 1/3工频

(d) 2/3工频

图12 不同ε值分岔图

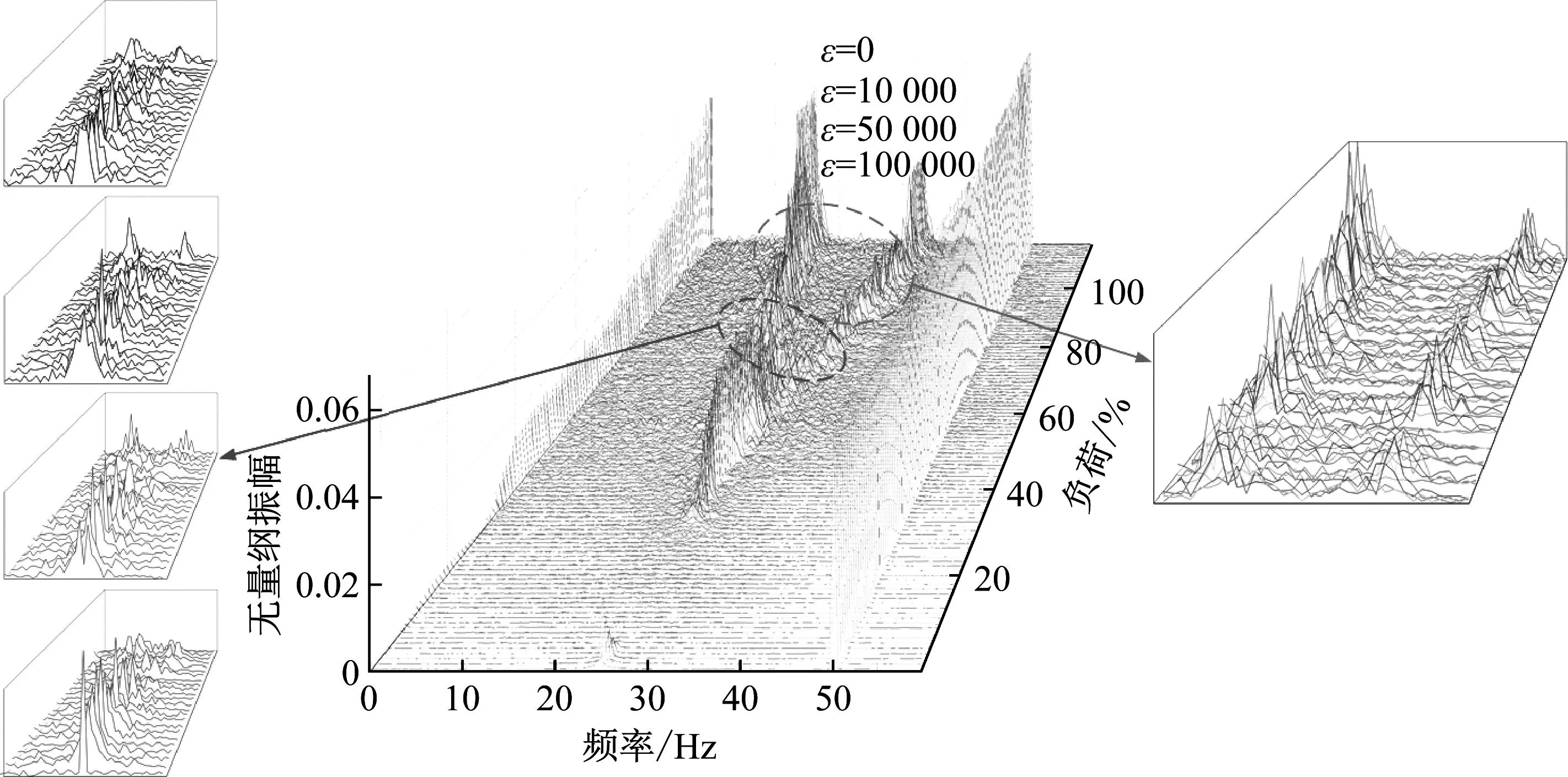
图13 不同ε值瀑布图

(a) 工频

(b) 1/2工频

(c) 1/3工频

(d) 2/3工频

2.3 耦合热、动载荷后系统的运动特性

为了解非线性刚度、阻尼的耦合作用,使研究更符合转子的实际工作情况,分析了耦合热、动载荷前后系统的运动特性。耦合热、动载荷后系统设计参数有一定变化如密封间隙、转子直径等。不仅使激振力发生改变同时改变了系统的非线性刚度、阻尼,如表5所示。研究中耦合热、动载荷汽流激振力获取流程如下：设计参数下密封流场计算,获得流场温度、压力分布;分析耦合后密封结构,获得耦合热、动载荷后密封腔尺寸变化;计算密封腔变形后的涡动流场,获得耦合后的激振力。

图15为耦合热、动载荷前后的分岔图。相比之下耦合后系统更早的进入了混沌二周期阶段,且此阶段转子位移略有减小。当转子进入复杂混沌周期后,耦合前系统转子位移更小尤其在60%～75%THA阶段。在高负荷区域耦合热、动载荷后的系统基本没有明显的运动趋势,但转子位移有所减小,说明耦合后系统流场更复杂难以形成明显的周期性运动,且汽流激振力更大,对转子位移有一定限制。

表5 耦合热、动载荷参数

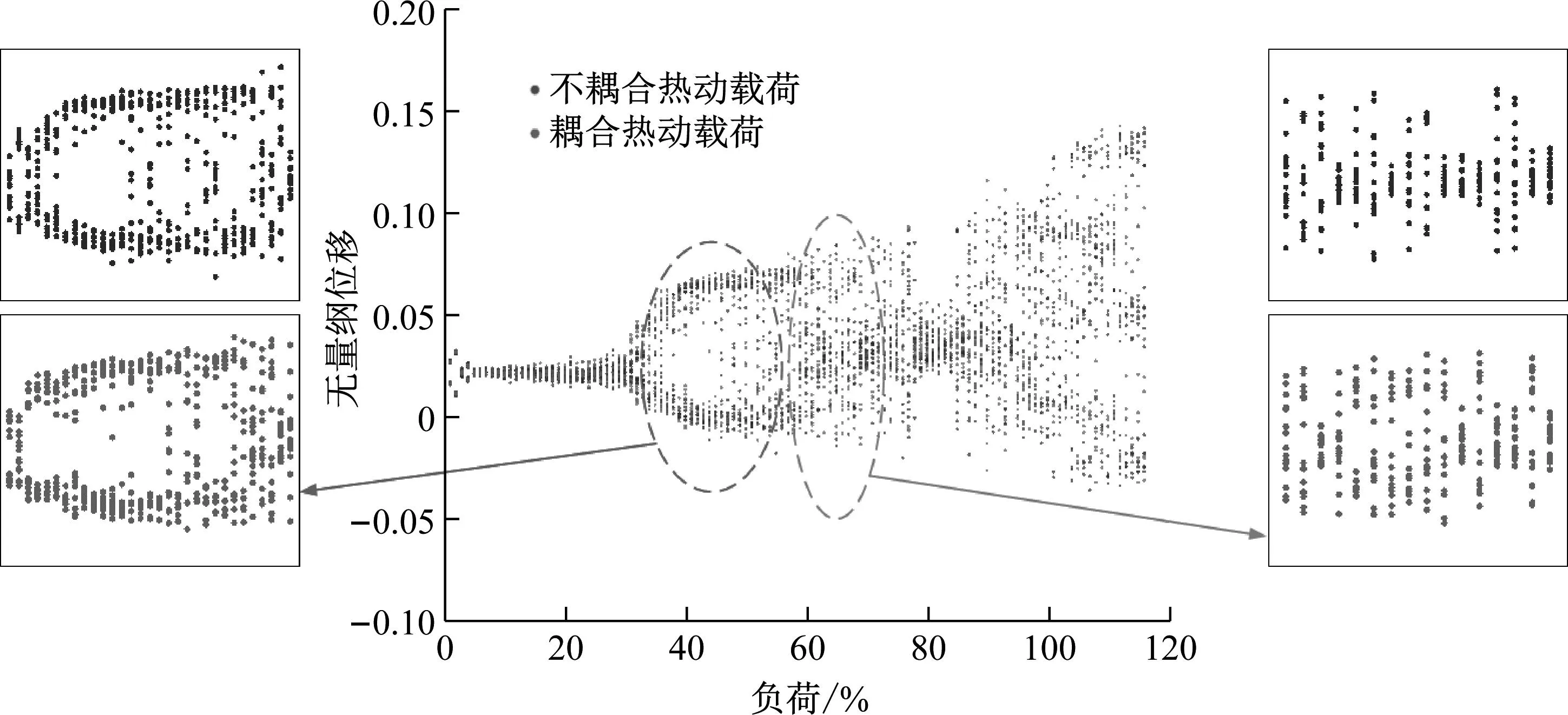
图15 耦合热、动载荷前后分岔图

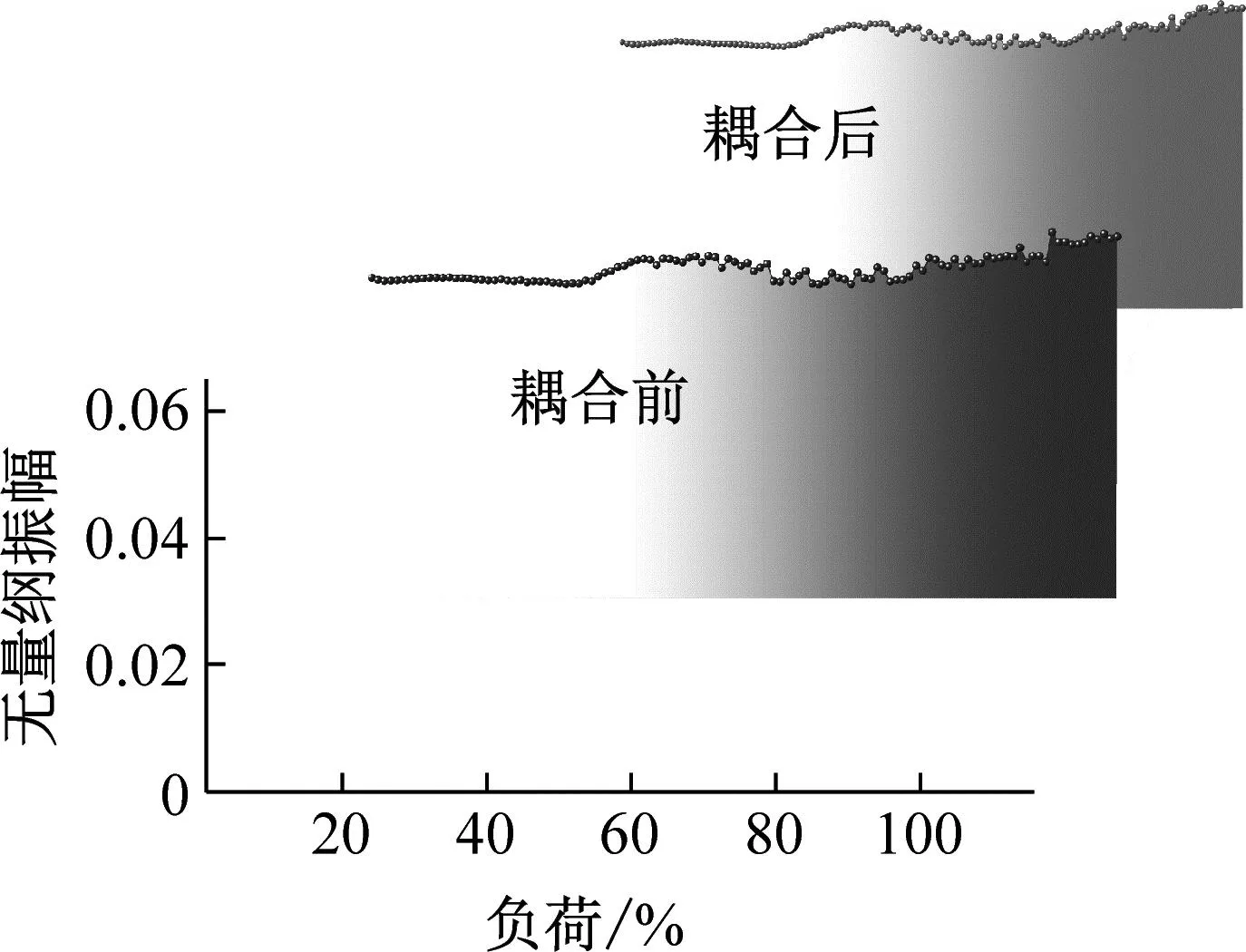
图16为耦合热、动载荷前后转子系统频率瀑布图,如图所示耦合前后系统均有明显密频现象,其中耦合后较高的密频区域主要集中在1/2工频向1/3、2/3工频转化初期与1/3工频前端区域,其它区域较为缓和,尤其是高负荷区域。这是因为耦合热、动载荷后密封间隙更小、密封内流场更复杂,汽流激振力较大非线性更强,且系统非线性刚度减小,在激振力作用为主的区域多频涡动体现明显。

图17为耦合前后主要频率无量纲振幅图,其中耦合后的1/2工频区域向低负荷方向有所移动且区域更小,这是由于考虑热、动载荷后激振力更大且增长更快,与油膜力耦合后使系统更早的出现1/2工频,更早的向其它工频演化。1/3、2/3工频耦合后的幅值有所降低,区域变化不大。

图16 耦合热、动载荷前后瀑布图

(a) 工频

(b) 1/2工频

(c) 1/3工频

(d) 2/3工频

3 稳定性分析

常用最大Lyapunov指数来衡量转子动力系统的稳定性,本次研究采用wolf法对其值进行计算。其值大于0代表系统处于混沌的、难以预测的随机运动;其值小于0则代表系统处于周期运动,属于可预测的有一定规律可寻的运动状态。混沌表示非线性系统在某种条件下呈现出难以预测的随机现象,是有序与无序融为一体的现象。

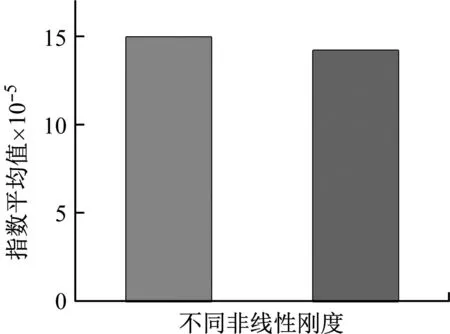
图18为不同非线性刚度最大Lyapunov指数曲线与指数平均值。如图所示虽然指数值很小低于10-3但大部分区域高于0,说明转子基本处于混沌状态。比较四种情况,在负荷低于30%THA区域指数变化不大,对比分叉图此时系统处于类似混沌一周期运动,汽流激振力较小非线性刚度的介入作用不明显。随着负荷的增加转子进入混沌二周期运动,此区域指数值均有所上升这说明混沌二周期运动更为复杂,系统稳定性波动明显。考虑非线性刚度后指数值有所下降但小于0的区域没有了,γ=3×109N/m3与γ=3×1011N/m3在57%THA处还出现了高峰值,说明非线性刚度对此区域转子的运动状态影响明显。当转子进入复杂混沌运动后,指数值有降低趋势还出现了小于0的稳定区域,说明此时系统运动的失稳特征减弱。而考虑非线性刚度后此区域指数值出现更多小于0区域,其中γ=3×1010N/m3时比较明显,说明合理的非线性刚度能够改善系统高负荷运行的稳定性。观察指数的平均值,考察非线性刚度后平均值有所上升,γ=3×1010N/m3时最低。

(a) 最大Lyapunov指数

(b) 指数平均值

图19为不同非线性阻尼的最大Lyapunov指数曲线与指数平均值。由图19(a)可知,考察非线性阻尼后指数值有所上升且波动变大,但也出现了更多指数小于0的区域,波动也随着ε值的增加有所改善。当系统负荷达到35%THA时ε=10 000 N·s2/m2、ε=100 000 N·s2/m2指数出现较高峰值,说明这两种情况转子在分岔过渡过程中稳定性较差。当达到67%THA时ε=10 000 N·s2/m2、ε=50 000 N·s2/m2出现高峰值。而后指数值有所下降并出现小于0区域。由图19(b)可知,考虑非线性阻尼后指数平均值明显上升,随着其值的升高逐步降低。总体来讲随着非线性阻尼值的增加系统的稳定性有所改善。

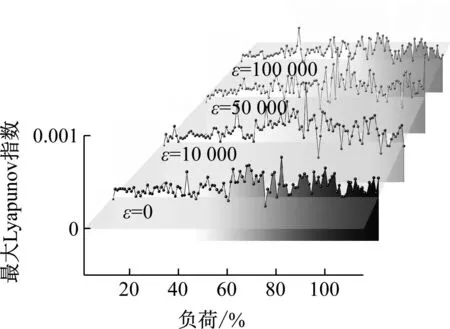
(a) 最大Lyapunov指数

(b) 指数平均值

图20考察了耦合热、动载荷前后的指数曲线与平均值。相比之下耦合前后低负荷区域指数值区别不大,系统进入混沌二周期运动后直至73%THA耦合后的指数值波动更明显且指数值更高并在50%THA处出现高值,对比分岔图耦合后的混沌二周期区域更长,说明混沌二周期蕴含的失稳因素更多更复杂。当系统负荷超过75%THA耦合后的指数值明显更低,且小于0的区域更多,说明耦合后的系统高负荷区域更稳定。这是由于耦合后非线性刚度变小阻尼变大,且密封腔内间隙更小,产生更大的汽流激振力对转子的涡动幅度产生了限制。

4 结 论

为更准确地反应超超临界汽轮机转子-轴承-密封系统的运动特性,本文改善了转子运动微分方程,并通过试验对比验证了方程的准确性。利用龙格-库塔法对其求解,讨论了不同非线性动态特性系数以及耦合热、动载荷后系统的运动特性与稳定性。具体结论如下：

(1) 通过对比不同条件下系统最大Lyapunov指数,系统均有失稳可能,且考虑非线性动态特性后其均值有所上升;其中一定范围内的非线性刚度能够改善系统的稳定性;而非线性阻尼值越高系统稳定性越好;耦合热、动后的系统高负荷区域更稳定。

(2) 系统中非线性动态特性系数会使转子不同类型的运动区域发生改变,非线性刚度在一定范围内可以减小转子的位移;而非线性阻尼会使混沌二周期区域增加,减小较高负荷区域转子的涡动幅值。对比耦合热、动载荷前后,高负荷区域耦合后的转子位移变小。

(a) 最大Lyapunov指数

(b) 指数平均值

(3) 考察不同条件下系统频率分布,存在1/2、1/3、2/3工频,且随着负荷的增加密频现象愈发明显。其中考虑非线性刚度后密频效果略有增加,但合适的非线性刚度值可以缓解此现象。考虑非线性阻尼后系统由1/2工频向1/3、2/3工频的分岔及演化过程中的高幅值密频随着其值的升高而减弱;耦合热、动载荷后明显的密频现象主要集中在激振力作用为主的工频区域。

(4) 系统中的非线性刚度、阻尼均会使1/2工频区域向高负荷方向移动且范围略有增加,1/3、2/3工频幅值降低,且非线性阻尼会缩小1/3、2/3工频区域;耦合热、动载荷后系统的1/2工频出现更早,更早的向其它工频演化。