三相导线-相间间隔体系直流融冰热特性有限元及脱冰动力响应分析

祝 贺, 廖汉梁, 张仁奇, 刘 城

(1. 东北电力大学 建筑工程学院, 吉林 吉林 132000; 2. 贵州电网有限责任公司电力科学研究院, 贵阳 550000)

导线直流融冰过程中,覆冰不断融化,通流导线所受冰荷载不断减少,当覆冰导线在局部脱冰时会形成一个冲击波,冲击波在传播的过程中,使薄弱的冰层发生脱落,相比自然条件下的覆冰导线脱冰速度更快,三相导线体系在融冰过程中相比单导线脱冰情况具有非对称性,不同短接方案导线体系的脱冰跳跃高度不同,严重的脱冰跳跃造成电气和机械事故。

若能获得导线体系温度特性和振动特性参数,设计输电导线直流融冰相间优化系统,将能够实现保证直流融冰过程安全运行的同时,对间隔棒长度和位置的精确设置来对相间距进行优化,达到保障导线体系在实际融冰情况下的电气和机械安全性能的研究成果及应用目的。

目前国内外针对输电导线非对称运行特性的分析较少,而且缺乏全面的三相导线-间隔棒耦合结构体系的理论计算实例和研究。理论方面,文献[1-3]建立不同输电线路直流融冰数学模型,对输电线路直流融冰过程数学模型以及融冰动态变化进行理论研究,研究融冰过程中温度特性以及对导线-间隔棒体系脱冰动力响应。仿真研究方面,董永星等[4-6]建立了分裂导线-间隔棒体系的有限元模型,研究了分裂导线在不同步脱冰时各子导线的脱冰跳跃高度、导线张力和导线束扭转角的影响因素及变化规律,得到线路档距和高差影响的导线脱冰跳跃高度。相间优化系统研究方面,高超等[7-10]研究对输电线路脱冰过程进行模拟试验,分析输电线路脱冰对输电线路的动力响应,相间间隔棒的布置方案对三相导线脱冰跳跃的抑制效果,取得最佳的间隔棒布方案。

以上研究都关注了融冰过程中温度分布特性以及脱冰振动特性,定量分析脱冰对输电线路的动力响应影响,同时对直流融冰方式以及相间间隔棒优化布置方案进行研究。但仍存在以下问题：导线直流融冰过程温度特性数学模型中,未考虑导线在融冰过程空气间隙传热的影响,若只计算导线和冰层的传热量,计算结果与实际偏差较大;未考虑导线在融冰过程中热膨胀导致结构特性矩阵的变化,从而使导线脱冰振动特性研究与真实情况悬殊;导线直流融冰过程振动特性的仿真分析中,现有的文献仅分析单根导线和各档间的脱冰动力响应,没有考虑到三相导线体系的脱冰动力响应,忽略了在实际直流融冰情况非对称运行特性的影响。

1 覆冰导线直流融冰过程热特性有限元分析

对导线直流融冰过程热特性进行分析,按照实际尺寸建立LGJ-400/50导线实体模型,分析导线在直流融冰过程中不同覆冰厚度对导线温度的变化情况。根据输电导线的实际螺旋特征及接触特性,本文建立的覆冰导线直流融冰过程热特性仿真实体模型如图1所示。导线实际股线参数如表1所示。

图1 覆冰导线直流融冰过程热特性仿真模型

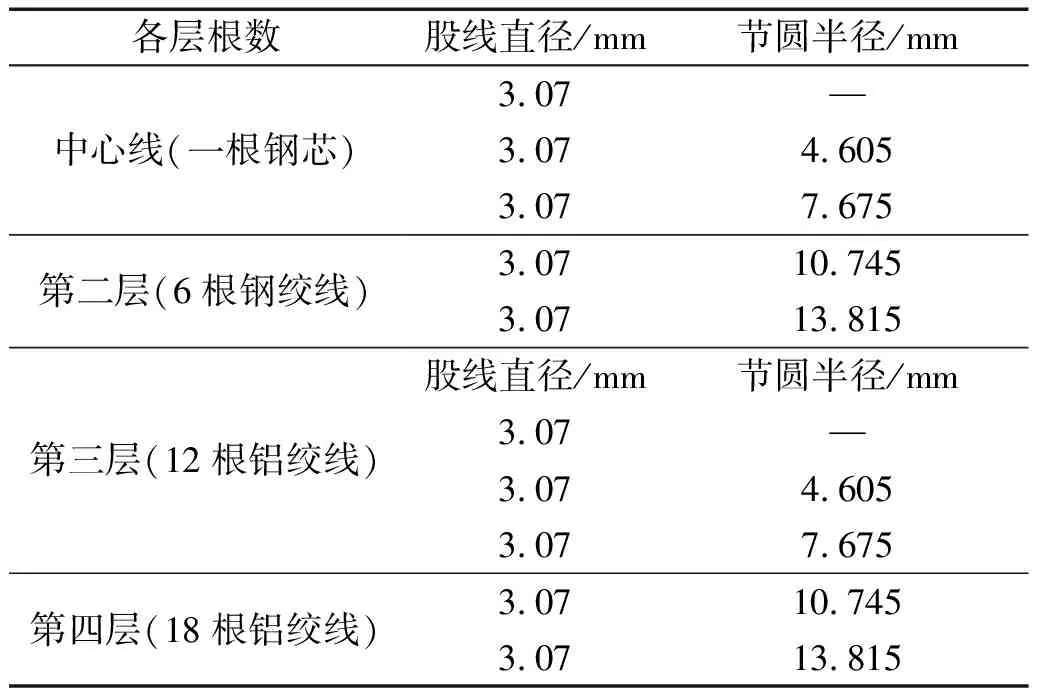
表1 LGJ-400/50导线实际股线参数

根据DL/T 5511—2016《直流融冰系统设计技术规程》,设计采用的JL/G1A400/50导线融冰电流：1035A,环境温度-5 ℃,风速5 m/s,使用COMSOL软件电流-温度模块进行分析[11-12]。

在导线仿真边界条件设置中,需要研究导线的焦耳热,因此将导线及冰层全域设置为电流守恒和固体传热,将冰层内侧与铝绞线外表面的接触面定义为电接触和热接触,设置通流后导线截面处的钢芯、铝层、冰层和空气间隙的传热系数等材料参数。定义导线一端为终端控制电流大小,另一端设置为接地,电势为0。导线两端截面设为固定截面,采用电磁热耦合模块,以此研究该段导线在接通电流后所产生的焦耳热[13-16]。

导线工作于外部高空中,且散热方式为对流传热,因此采用外部自然对流边界条件,介质设置为干空气,散热方式设置为沿导线长度方向,环境参数按照中国南方电网有限责任公司某500 kV输电线路实际监测数据进行设计：外部温度30 ℃、1个标准大气压、晴空太阳辐照度1 000 W/m2。

分析导线在直流融冰过程中不同覆冰厚度对导线温度的变化情况,不同覆冰厚度下融冰开始阶段、融冰最后阶段和脱冰后阶段覆冰导线温度分布如图2、图3和图4所示。

图2、图3和图4为直流融冰不同阶段融冰电流作用下导线温度变化情况。导线温度在融冰时非均匀分布,导线上表面与冰层接触进行传热,导线下表面覆冰融化在重力作用下产生空气间隙,下表面与空气间隙间进行传热。受重力影响,导线冰层逐渐脱落。在融冰过程中,随融冰时间的增加,冰层与导线之间的空气间隙逐渐变大,导线下表面的温度较高与上表面。导线中心点位置的热量向周围散发较慢,因此导线中心点的温度最高。

对比图2和图3, 覆冰厚度越厚,温度变化越缓慢,融冰阶段中覆冰厚度为5 mm、10 mm、20 mm对应冰层的温度分别为-2.980 ℃、-3.576 ℃、-5.676 ℃,相比于升温阶段,温度分别升高17.33%、9.99%、7.62%,覆冰厚度越厚,温度上升的变化率越小。

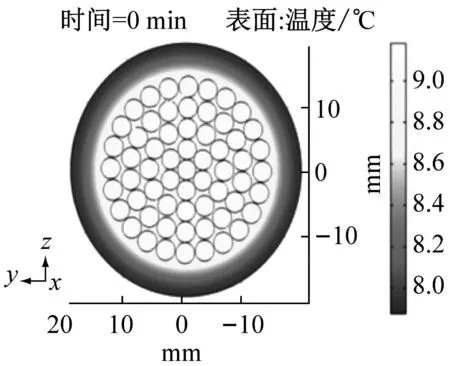
(a) 5 mm

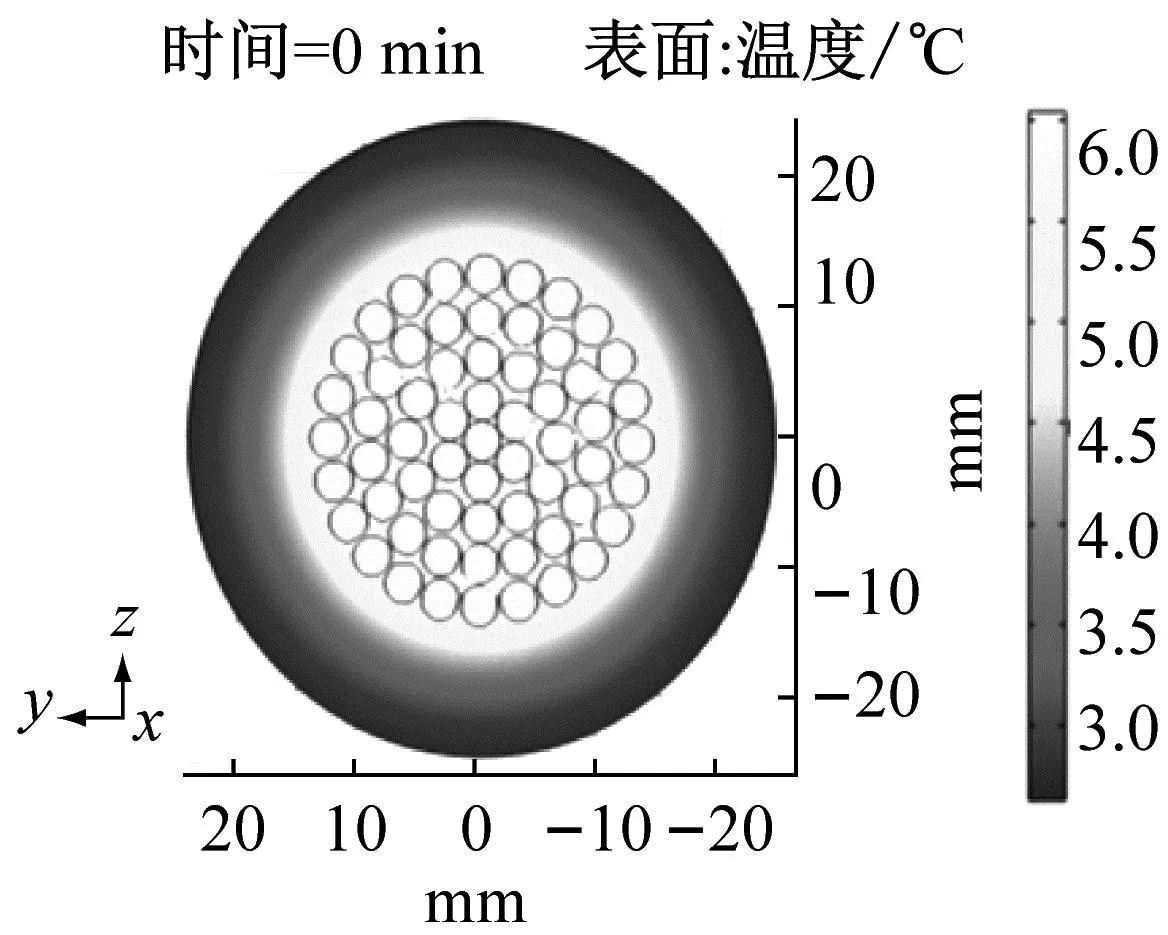
(b) 10 mm

(c) 20 mm

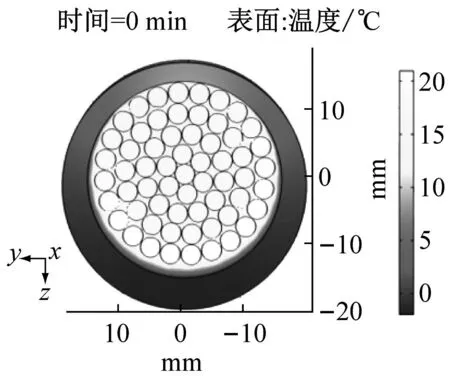
(a) 5 mm

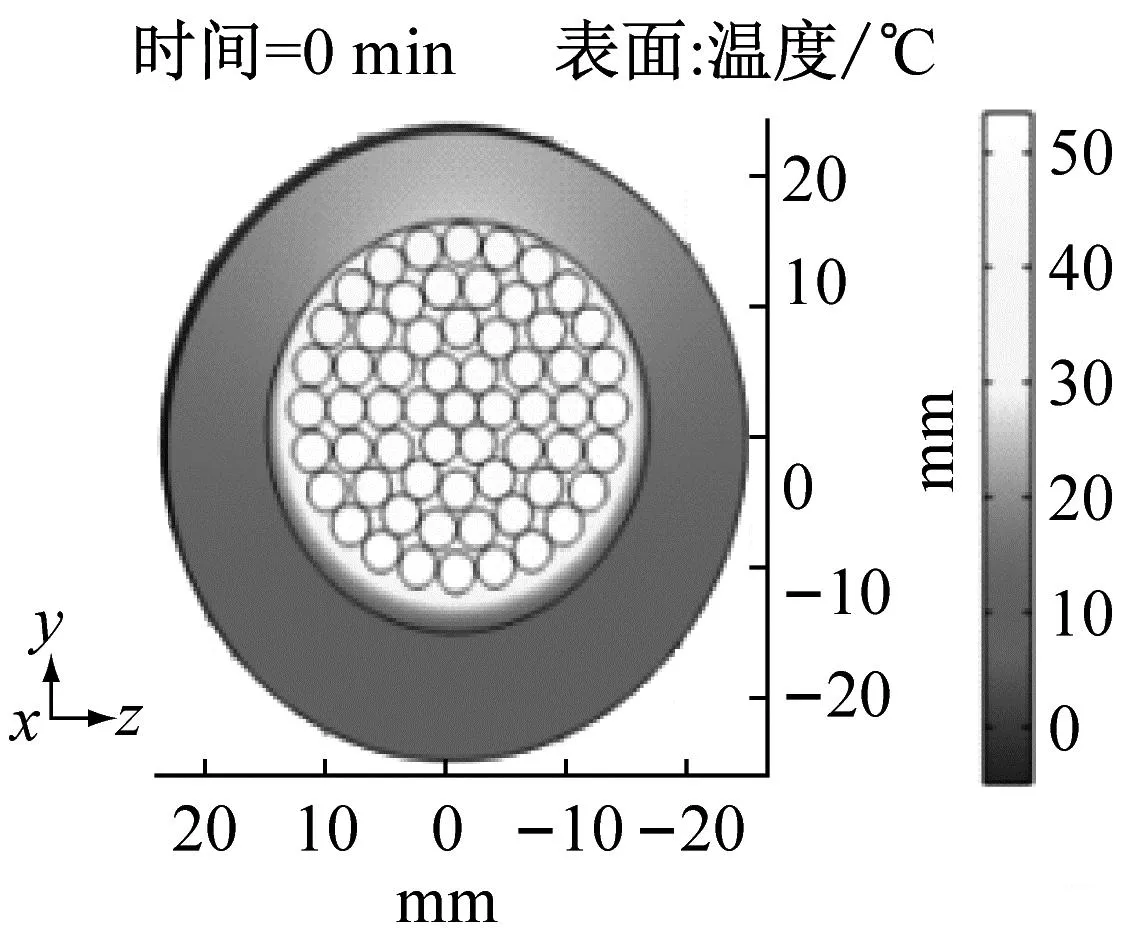
(b) 10 mm

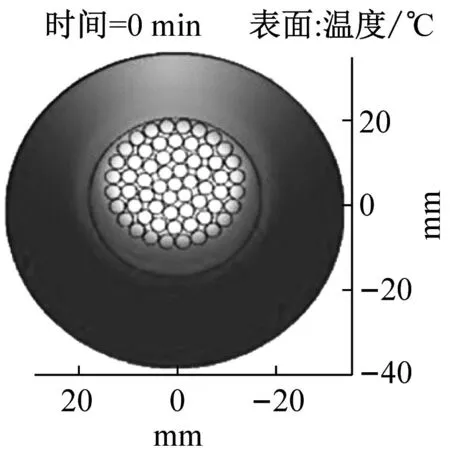
(c) 20 mm

(a) 5 mm

(b) 10 mm

(c) 20 mm

2 覆冰导线直流融冰过程热特性仿真计算分析

对导线直流融冰过程热特性影响因素进行分析,为更准确地了解导线直流融冰过程热特性,明确融冰时导线内部的温度变化情况,通过控制变量法,计算导线中心温度随时间变化情况,计算分析导线直流融冰过程下不同因素对导线融冰电流及导线融冰时间的变化规律。

计算风速5 m/s,冰厚20 mm,融冰电流1 035 A条件下,在不同环境温度下,导线中心点温度随时间变化情况,如图5所示。

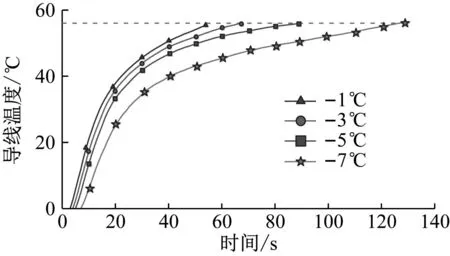
图5 不同环境温度导线中心点温度变化曲线

由图5可知,环境温度为-1 ℃、-3 ℃、-5 ℃、-7 ℃的情况下,融冰时间为30 s时,导线中心点温度分别为47 ℃、43 ℃、37 ℃、32 ℃,融冰时间为50 s时,温度分别升高12.7%、16.2%、27.2%、25%。

计算-5 ℃环境温度、冰厚20 mm,融冰电流1 035 A条件下,在不同环境温度下,导线中心点温度随时间变化情况,如图6所示。

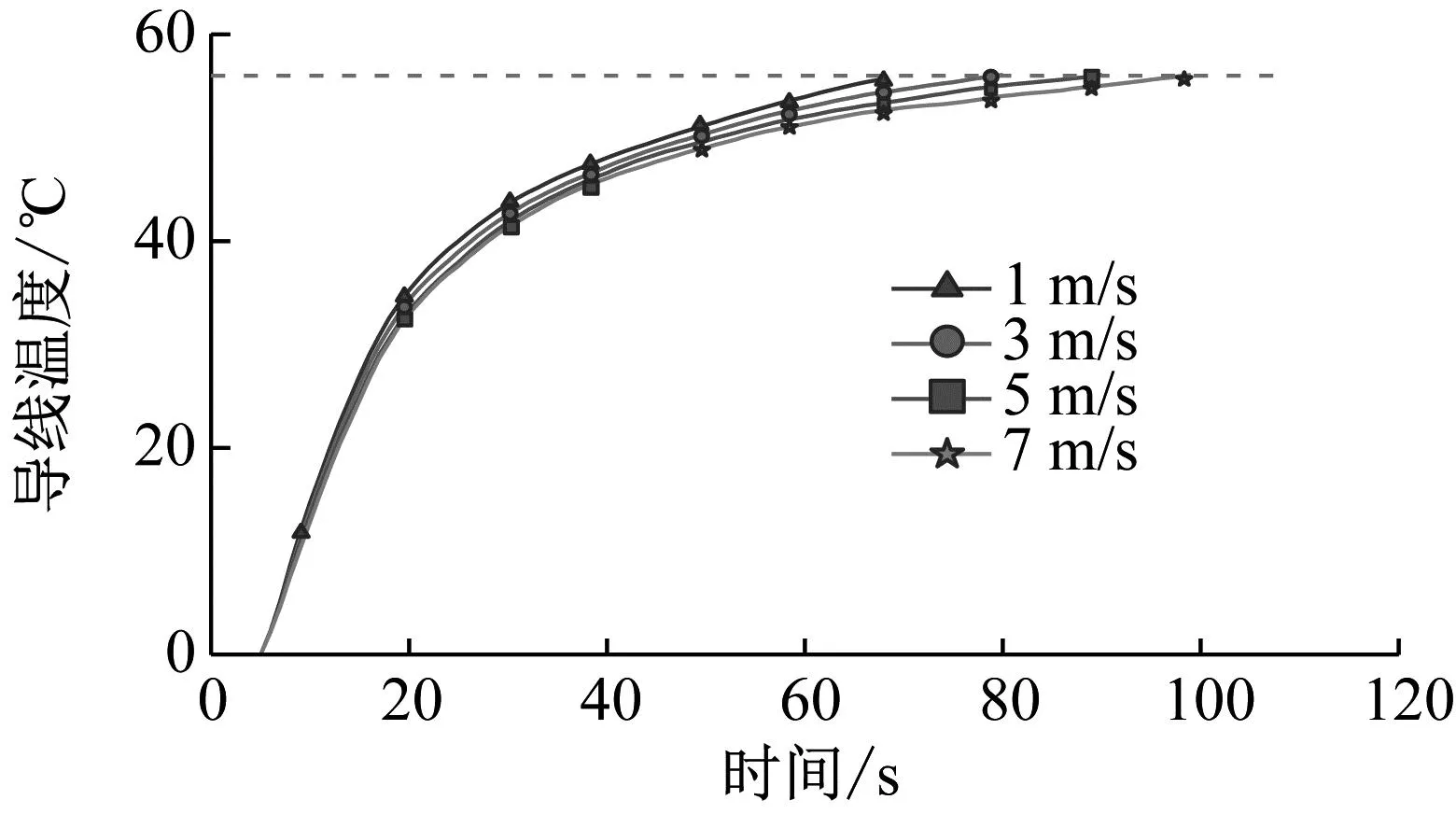
图6 不同环境风速导线中心点温度变化曲线

由图6可知,环境风速为1 m/s、3 m/s、5 m/s、7 m/s的情况下,融冰时间为40 s时,导线中心点温度分别为45 ℃、43 ℃、40 ℃、37 ℃,融冰时间为70 s时,温度分别升高17.7%、20.9%、25.2%、35.2%。

对比图5和图6,导线中心点温度的上升速度随环境温度的降低而变慢 ,环境温度只会影响导线直流融冰过程中温度的上升速度以及融冰时间,不影响导线内部脱冰时刻的温度。导线中心点温度随风速增加而降低,导线中心点温度受风速的影响较小,不同风速下导线脱冰时刻的温度情况不变。

计算温度为-5 ℃、风速为5 m/s,覆冰厚度为20 mm条件下,在不同融冰电流作用下,对导线中心点温度变化情况。如图7所示。

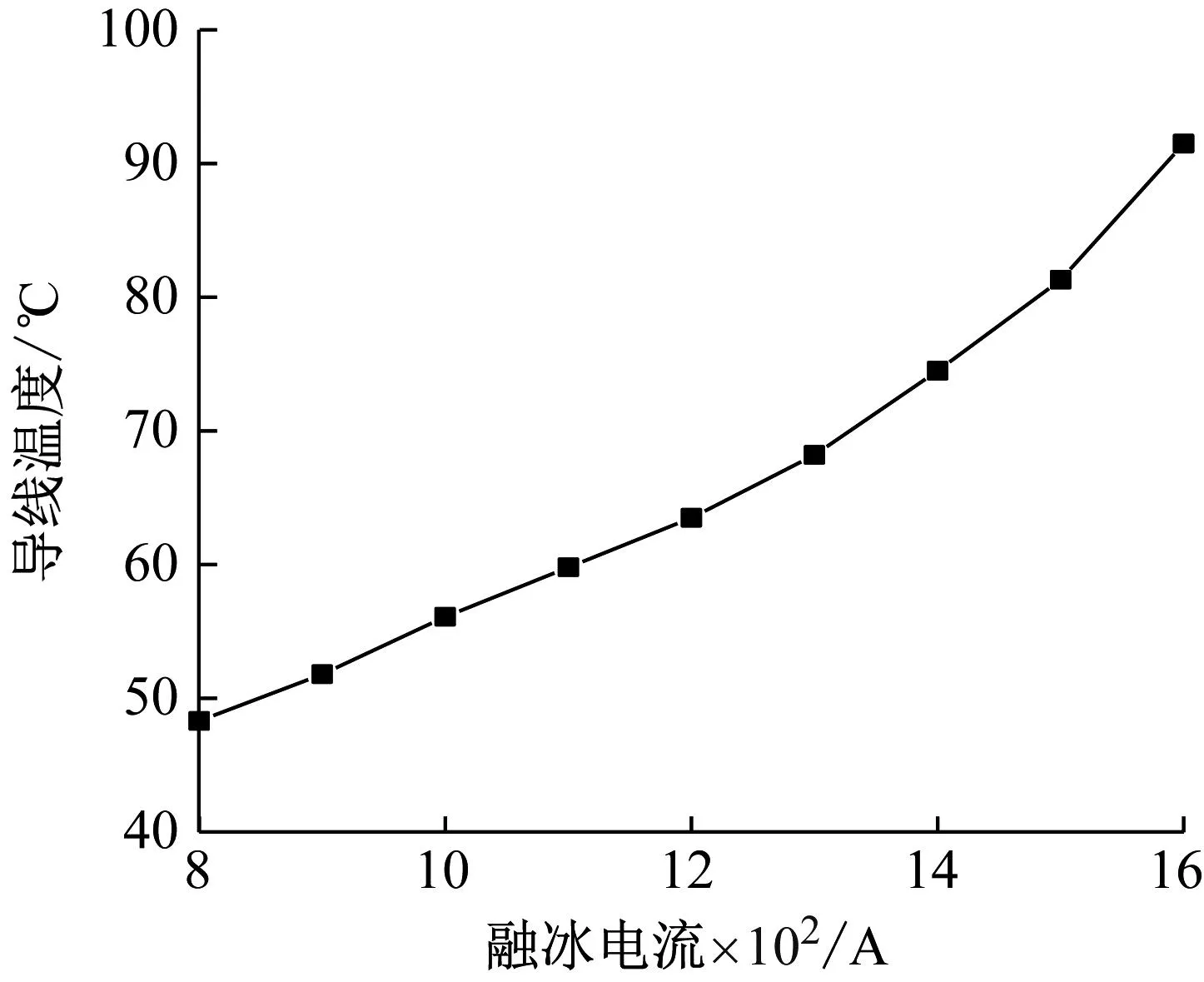
图7 不同融冰电流导线中心点温度变化曲线

由图7可知,融冰电流对融冰温度的影响呈现非线性,导线通以电流之后由于电阻的存在会产生焦耳热,热量通过冰层传到冰的表面,随着融冰电流的增大,冰层初始融化时间逐渐趋于饱和,导线中心点温度随融冰电流的增加而升高,因融冰电流越大,产生的焦耳热越多,而导线的散热系数是其传导热量的固有能力,在通以融冰电流时将保持不变,这进一步导致了导线中心点温度的升高。对于融冰电流需要合理选择,防止因融冰电流过大造成导线损伤。

3 三相导线-相间间隔体系脱冰动力响应有限元模拟

利用导线温度分布数据进行曲线拟合,得到脱冰时刻导线温度作为初始条件施加,分析三相导线-相间间隔体系不同工况下直流融冰非对称脱冰动力响应。

3.1 三相导线-相间间隔体系有限元模型

三相导线-相间间隔体系建模过程中,相间间隔棒与导线连接处的梁单元和索单元之间定义beam连接关系。考虑间隔棒对导线之间的约束,间隔棒布置位置按照500 kV输电线路实际工程情况进行布置。在有限元建模过程中,结合南方电网实际运行参数,对输电线路和脱冰参数进行确定,将输电导线的档距取为200 m,导线型号为LGJ-400/50,采用FXJGB-35/70型间隔棒,各相导线之间间距为2 500 mm,间隔棒具体参数如表2所示。

表2 FXJGB-35/70相间间隔棒物理特性参数

考虑到500 kV输电线路采用的2×LGJ - 400/50双分裂导线,分析实际融冰时,三相导线为三角形排列时非对称脱冰的动力响应,等效单导线图如图8所示。

图8 分裂导线和等效单导线图

由图8可知,为了简化计算,将每相中的双分裂导线等效简化为单导线,简化时需要满足导线等效截面积相等及覆冰质量相等的原则[17-22]。计算将间隔棒总重平均分配到三根等效圆棒上,通过已知的间隔棒重量及铝合金密度,计算得出等效圆棒的截面半径尺寸,通过铰接方式与导线进行连接。导线采用SOLID45单元进行模拟,采用SOLID45单元为了更好的模拟实际融冰过程中导线的情况,冰单元采用SOLID45进行模拟,通过ANSYS有限元软件中布尔运算将其与钢芯铝绞线合为一体,使导线和冰之间共节点,不产生相对滑移,覆冰导线有限元模型如图9所示。

图9 三相导线-相间间隔体系有限元模型图

对三相导线-相间间隔体系中相导线进行编号,分别讨论单相导线脱冰、两相导线脱冰、三相导线脱冰不同工况下,导线体系的脱冰动力响应,具体相导线编号命名情况如图10所示。

图10 三相导线-相间间隔体系网格划分图

3.2 有限元模型准确性验证

为验证有限元模型的准确性,需要取以往直流融冰下导线的结果进行分析对比,实际直流融冰条件不易模拟,导致目前对直流融冰导线动态响应试验数据较少。通过与Meng等在武汉国家电网研究中心建立的等比例235 m档距输电导线脱冰动态特性试验结果进行对比分析。对比图如图11所示。试验中通过等效重力法将覆冰质量计算,由实际沙袋重物进行覆冰等效,通过电动切割器控制悬挂重物钢绳模拟覆冰脱落。

图11 有限元数据与试验数据对比图

选取Meng等试验中的B-3工况进行验证,试验中其档距为235 m的LGJ-630/45钢芯铝绞线,覆冰厚度15 mm,单档100%脱冰,通过在有限元软件中按B-3工况建立完全一致计算模型,将导线两端施加三自由度约束,采用布尔运算将冰层附加在导线上,通过生死单元法,杀死覆冰单元模拟覆冰脱落,计算时将导线平均划分为100个单元,计算时间步长为0.05 s。

本文采用SOLID45单元建模进行生死单元法模拟覆冰脱落的计算模型与Meng等进行的脱冰试验结果吻合较好,导线脱冰跳跃高度及趋势保持一致,说明此方法模拟的准确性,为下文分析奠定基础。

4 三相导线-相间间隔体系覆冰脱落响应分析

结合南方电网实际操作过程中融冰经验,在有限元计算过程中对于LGJ-400/50导线直流融冰,单导线融冰电流采取1 000 A进行融冰,双分裂导线则应采取单导线融冰电流的二倍大小进行融冰。采用生死单元法,杀死覆冰单元模拟覆冰脱落。研究参数包括三相导线-相间间隔体系中单相导线脱冰、两相导线脱冰、三相导线脱冰不同工况下的情况。

4.1 基于解析法的导线最低点确定

通过悬链线方程可以计算得到导线最低点到左侧和右侧悬挂点的距离分别为

(1)

式中,a,b分别为最低点到左侧和右侧悬挂点的距离。

最低点到原点的垂直高度y0为

(2)

式中,β为两悬挂点间的高差角。

因此,覆冰后导线总荷载P1和比载γ1为

(3)

式中,A为导线总截面积,可以根据导线型号查询到。

在输电线路覆冰后,导线水平应力和线长也都会发生变化,覆冰后水平应力可以通过覆冰前后的状态方程求解

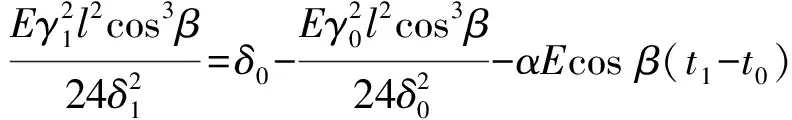
(4)

式中：δ1为覆冰导线水平应力;E,α分别为导线的综合弹性系数和温度膨胀系数,可以通过导线型号查询到;t0和t1分别为覆冰前后导线温度。对于连续档导线,可根据邵天晓[23]中连续档导线的状态方程求取各档的水平应力。

覆冰后导线线长为

(5)

将式(3)～(5)代入式(1)和(2),可以得到覆冰后一档有高差输电线路的最低点坐标。

4.2 单相导线脱冰分析

选取A相导线进行脱冰,对三相导线弧垂最低点导线情况进行分析。

由图12可知,A相导线脱冰时,ABC三相导线在经历短暂的震荡后振动基本趋于停止,导线体系最大垂直向跳跃高度在脱冰后阶段到达稳定值2.76×10-3m。

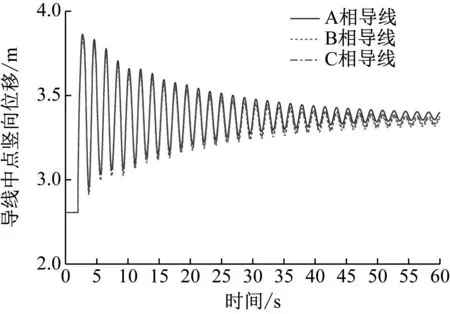
图12 A相导线脱冰时导线弧垂最低点垂直位移时程

由图13可知,A相导线脱冰时,ABC三相导线的横向摆幅的位移基本呈对称趋势,最大横向摆幅的位移仅为3×10-3m。

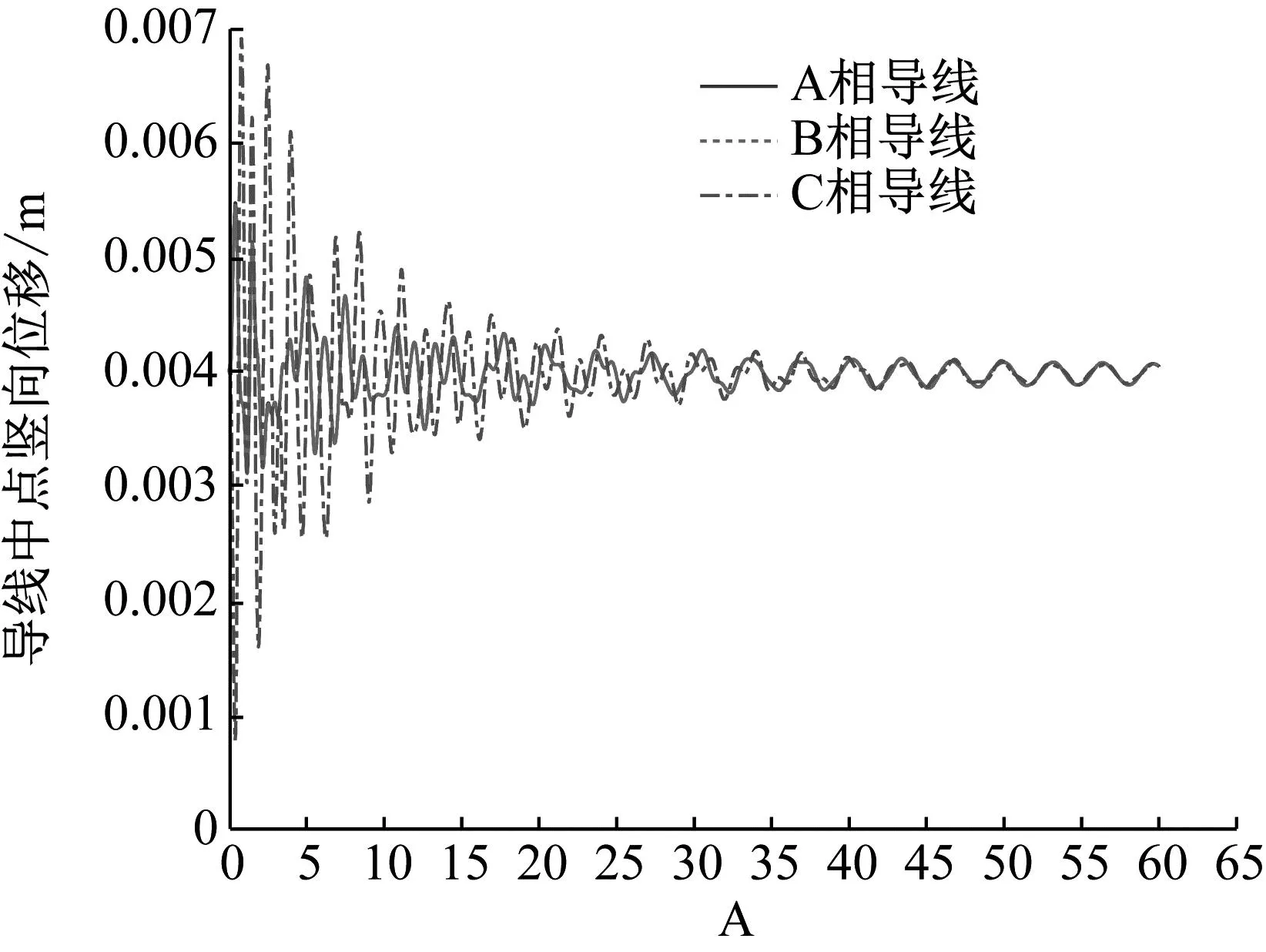
图13 A相导线脱冰时导线弧垂最低点水平位移时程

4.3 两相导线脱冰分析

选取A、B相导线进行脱冰,对三相导线弧垂最低点导线情况进行分析。

由图14可知,A相与B相导线脱冰时,脱冰相导线A、B相的竖向跳跃高度位移与未脱冰相导线C相导线振动趋势相同,但最大脱冰跳跃高度存在差异,脱冰相导线A相较未脱冰相导线C相最大脱冰跳跃高度差值为3.5×10-3m。

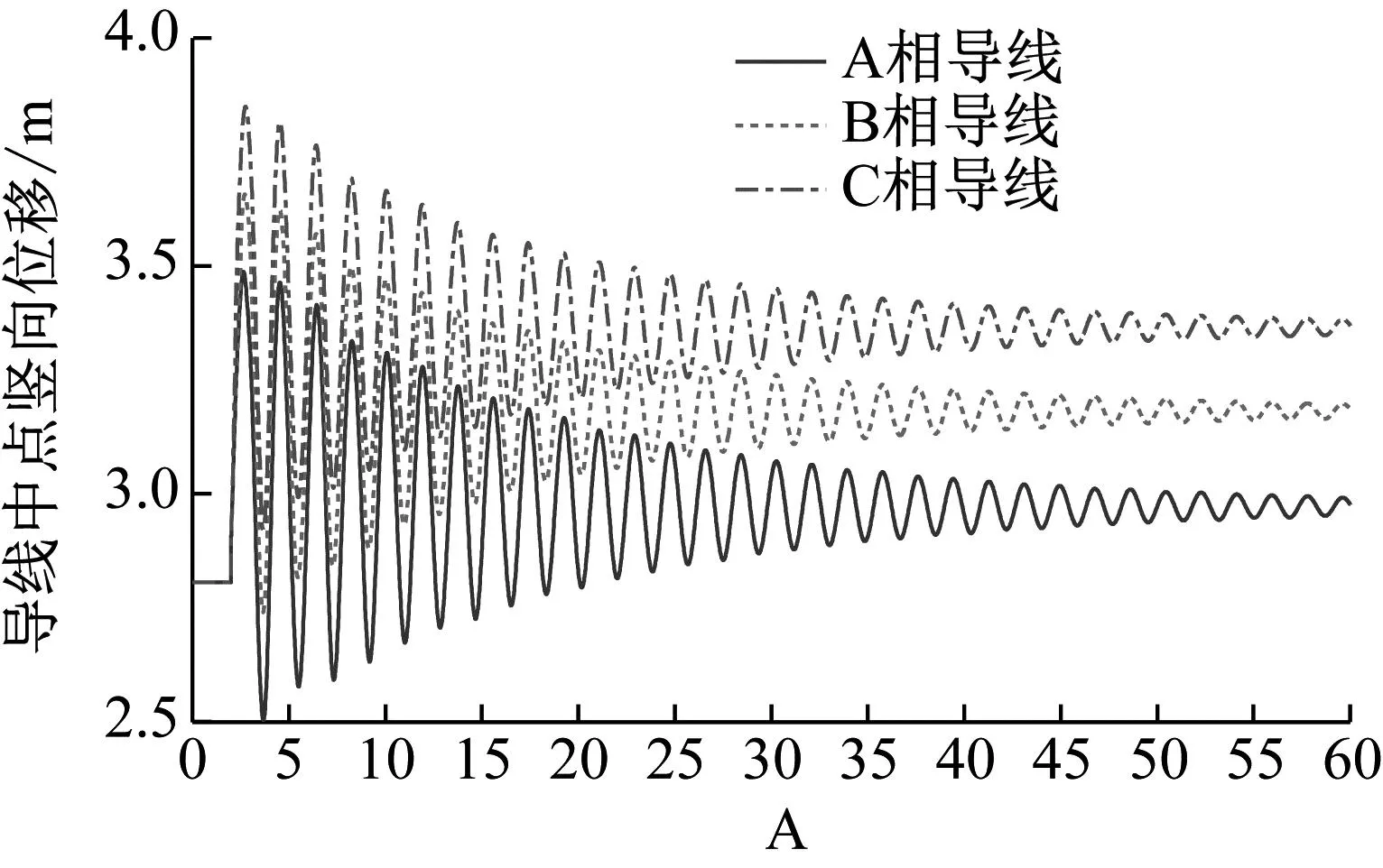
图14 A、B相导线脱冰时导线弧垂最低点垂直位移时程

由图15可知,A相与B相导线脱冰时,ABC三相导线的横向摆幅的位移基本呈对称趋势,最大横向摆幅的位移仅为3×10-3m。

图15 A、B相导线脱冰时导线弧垂最低点水平位移时程

5 结 论

本文先利用COMSOL多物理场仿真软件对覆冰导线直流融冰过程热特性有限元分析,得到导线温度分布数据进行曲线拟合,提取脱冰时刻导线温度作为初始条件施加于ANSYS有限元软件,采用 ANSYS 有限元软件中LS-DYNA PrepPost 模块,进行非线性结构动力学分析,进行覆冰导线找形分析,施加融冰电流采用生死单元法模拟覆冰脱落,对三相导线-相间间隔体系计算,分析不同脱冰相数导线的位移时程曲线,并得出以下结论：

(1) 融冰电流越大,覆冰厚度越厚,脱冰时刻导线内部的温度越高;环境风速影响直流融冰过程中温度的上升速度以及融冰时间,导线中心点位置的热量向周围散发较慢,导线中心点的温度最高,不影响导线内部脱冰时刻的温度。

(2) 三相导线-间隔棒体系脱冰时,在单相导线脱冰情况下,三相导线-间隔棒体系在经历短暂的震荡后振动基本趋于停止,导线体系最大垂直向跳跃高度在脱冰后阶段到达稳定值2.76×10-3m。在两相导线脱冰情况下,脱冰相导线A、B相的竖向跳跃高度位移与未脱冰相导线C相导线振动趋势相同,但最大脱冰跳跃高度存在差异,在三相导线-间隔棒体系实际融冰操作过程中,建议选择单相导线脱冰,避免导线覆冰脱落时,三相导线-间隔棒体系发生扭转现象。

(3) 导线融冰过程温度分布沿径向与轴向分布不均匀,考虑导线在融冰过程空气间隙传热的影响,计算结果与实际偏差较大,轴向温度呈先升高后降低的趋势,温度随导线弧长位置变化。