应用光谱指数和机器学习反演紫丁香叶片的叶绿素面密度1)
杜菲菲 安慧君 李贺新
(内蒙古农业大学,呼和浩特,010020)(内蒙古第二林业和草原监测规划院)
紫丁香(SyringaoblataLindl.)是木犀科丁香属植物,为落叶灌木或小乔木。因其独特的观赏价值和较强的环境适应性,被广泛应用于我国北方各省区的城市园林绿化[1]。作为城市绿化应用最普遍的花木之一,对其生长状态的监测尤为重要。研究表明[2],植物体内叶绿素含量能够反映植物的营养状况和生理代谢水平。传统的叶绿素含量测定方法费时费力且难以大面积开展,20世纪末出现的高光谱技术能对植被进行微弱光谱差异的定量分析,具有信息获取量大、实时、无损等优势,弥补了传统方法的局限性。
高光谱技术在叶绿素含量预测方面的研究,大多建立在一维层面[3-4],对原始或预处理光谱提取敏感波段或全波段进行建模,但由于输入参数过多导致模型较为复杂。随着研究的深入[5-8],二维光谱指数得到了发展,因其考虑到了光谱间的重叠吸收和相互影响,提高了对叶绿素的敏感程度,且经筛选出的最优光谱指数能够有效降低模型复杂程度。有研究表明构建和筛选全波段三维光谱指数在土壤有机质含量[9]、土壤含水率[10]预测方面比二维更有优势,但在叶绿素含量预测方面尚未有研究。近年来,机器学习算法在解析光谱参数与叶片生化组分之间的非线性问题时表现能力较一元和多元线性回归好,如反向传播神经网络(BPNN)、支持向量回归机模型(SVR)等。其中,2007年由Jayadeva提出的孪生支持向量回归机(TSVR)模型[11]有良好的泛化性能,其运行效率是SVR的4倍,在金融[12]和工业[13-14]领域能很好地反映特征指标的非线性响应,但在植物生理含量预测方面尚未有研究。
本研究以内蒙古农业大学东校区内紫丁香为研究对象,测定叶片反射率和叶绿素面密度,在一维和二维光谱指数的基础上,引入三维光谱指数,基于原始光谱(R)及其对应的一阶微分(RFD)、二阶微分(RSD)光谱构建全波段不同维度的光谱指数,通过皮尔逊相关系数法(PCC)进行最优光谱指数筛选,构建基于最优光谱指数和孪生支持向量回归机(TSVR)的紫丁香叶片叶绿素面密度反演模型。为进一步加强模型的稳定性和泛化能力,采用海洋捕食者[15]仿生优化算法(MPA)对TSVR进行优化[16],提出MPA-TSVR融合模型,并与PLSR、SVR、TSVR模型进行对比,得到最优模型。旨在量化不同维度的光谱指数对紫丁香叶片叶绿素面密度的响应,拓宽优化算法融合机器学习算法在植物生理预测方向的研究,为城市绿化植物叶片叶绿素面密度反演提供新的思路与理论依据。
1 材料与方法
1.1 数据采集
试验在7月下旬开展,在内蒙古农业大学东校区内无遮挡开阔绿地上选择5丛生长正常且冠幅约2 m的紫丁香。每丛按树冠中心分为8个方位,每一方位在表层选4枚生长正常的叶片,每丛采集32枚,共采集160枚;叶片采集完成后放入已编号的塑封袋中当即带回实验室,用蒸馏水反复清洗后晾干。用ASD公司生产的FieldSpec4 Hi-Res波谱仪采集叶片反射光谱(350~2 500 nm);每枚叶选取3个样点,每个样点用植物探头测量3次;仪器每隔5 s记录1次数据,每隔10 min进行1次白板校正。紫丁香叶片叶绿素面密度测定采用分光光度法[15-16],与光谱采集同步进行。
1.2 光谱数据预处理
为消除原始光谱数据(R)受到杂散光、仪器噪声、基线漂移等因素的干扰,本研究对原始光谱数据进行光谱曲线的一阶微分(RFD)及二阶微分(RSD)预处理,以降低基线漂移,突出光谱特征[6]。除此之外,剔除位于两端(350~399 nm和2 401~2 500 nm)存在高频噪声的数据[7],并将得到的光谱数据(400~2 400 nm),按5 nm的间隔重采样,以降低光谱数据的冗余[9-10]。
1.3 光谱指数构建与筛选
选择3个二维光谱指数(IDI、ISRI、INDI)和3个三维光谱指数(ITBI1、ITBI2及ITBI3),对R、RFD和RSD分别构建全波段光谱指数[8-10],计算如式(1~6)。用皮尔逊相关系数法(PCC)分析光谱指数与叶绿素面密度间的相关系数(r),并以最大相关系数(rmax)为标准对构建的光谱指数进行变量筛选,减少冗余变量,消除共线性[20]。
IDI(Rλ1,Rλ2)=Rλ1-Rλ2,
(1)
ISRI(Rλ1,Rλ2)=Rλ1/Rλ2,
(2)
INDI(Rλ1,Rλ2)=(Rλ1-Rλ2)/(Rλ1+Rλ2),
(3)
ITBI1(Rλ1,Rλ2,Rλ3)=(Rλ1-Rλ2)/(Rλ2+Rλ3),
(4)
ITBI2(Rλ1,Rλ2,Rλ3)=(Rλ1-Rλ2)/(Rλ1+Rλ3),
(5)
ITBI3(Rλ1,Rλ2,Rλ3)=Rλ1/(Rλ2+Rλ3)。
(6)
式中:Rλ1、Rλ2和Rλ3为400~2 400 nm中任意波长下的反射率。
1.4 模型的建立
海洋捕食者算法(MPA)是一种仿生智能算法[14-15],与其他优化算法相比,MPA能有效的提升优化效果,能高效地获取更优的解。MPA在初始化种群后根据捕食者和猎物的不同速度比进行优化,过程分为3个阶段。
(1)勘探阶段。此阶段I∈(0,Imax/3),猎物移动速度与捕食者移动速度之比较高,该阶段为全局搜索阶段,模型为:
(7)
式中:Ei代表捕食者种群;Pi为猎物种群;捕食者和猎物种群中个体数均为n;Si为运动的步长;NR表示布朗运动,服从正态分布;D为常数项,通常取D=0.5;N∈[0,1],服从均匀分布;I为当前迭代次数;Imax为最大迭代次数;⊗表示逐项相乘。
(2)勘探转向开发的过度阶段。此阶段I∈(Imax/3,2Imax/3),猎物移动速度与捕食者移动速度相近。捕食者通过布朗运动搜索猎物,猎物通过莱维运动更新自身的位置。此阶段兼顾全局搜索与局部搜索寻优,使用公式(8)进行局部寻优,使用公式(9)进行全局搜索。
局部寻优模型:
(8)
式中:NL为服从莱维分布的随机数的向量,表示莱维运动。
全局搜索模型:
(9)
式中:CF表示步长的自适应参数,计算公式为:
(10)
(3)开发阶段。该阶段I∈(2Imax/3,Imax),猎物移动速度与捕食者移动速度之比较低,捕食者主要进行局部寻优,数学模型为:
(11)
此外,在每次迭代结束后,MPA通过利用鱼群聚集装置效应(FADs)使捕食者进行更长的跳跃,以避免陷入局部最优。数学模型:
(12)
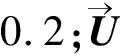

f1(x)=(w1,x)+b1,
(13)
f2(x)=(w2,x)+b2,
(14)
式中:x∈Rn,w1和w2表示权重,b1和b2表示偏置,(.,.)表示内积。
通过求解如下问题即可得到最优决策函数:
(15)
(16)
式中:‖·‖表示L2范数,C1、C2是惩罚参数,ε1、ε2>0是常数,ξ、θ是松弛向量,e是m×1维单位列向量。
通过引入拉格朗日乘子δ、η,根据Karush-Kuhn-Tucker(KKT)条件得到如下对偶形式:
(17)
(18)
式中:G=[Ae],h1=y-ε1e和h2=y+ε2e,式(5)和(6)的最优解分别为:
(19)
(20)
求解出f1(x)和f2(x)后,决策函数如下:
(21)
在非线性情况下,通过引入核函数映射到高维空间进行求解,即输入矩阵A∈Rm×n变为K(A,AT),式(1)和(2)变为:
f1(x)=K(xT,AT)w1+b1,
(22)
f2(x)=K(xT,AT)w2+b2。
(23)
相应的决策函数与式(21)类似。
应用MPA-TSVR对紫丁香叶片叶绿素面密度反演模型构建。
(1)模型输入参数及数据集划分
把以不同预处理方法和不同维度为标准筛选出的最优光谱指数分别作为输入参数构建模型。将160个样本随机划分,选取80%的数据作为训练集(128个样本)用于模型训练,其余20%作为测试集(32个样本)用于模型性能评估,数据集划分如表1所示。本研究中所有试验均采用此标准划分数据集。
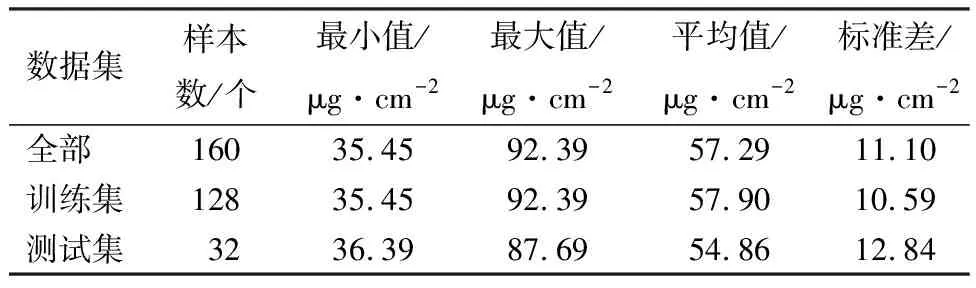
表1 紫丁香叶片叶绿素面密度实测数据集划分统计
(2)模型内置参数优化
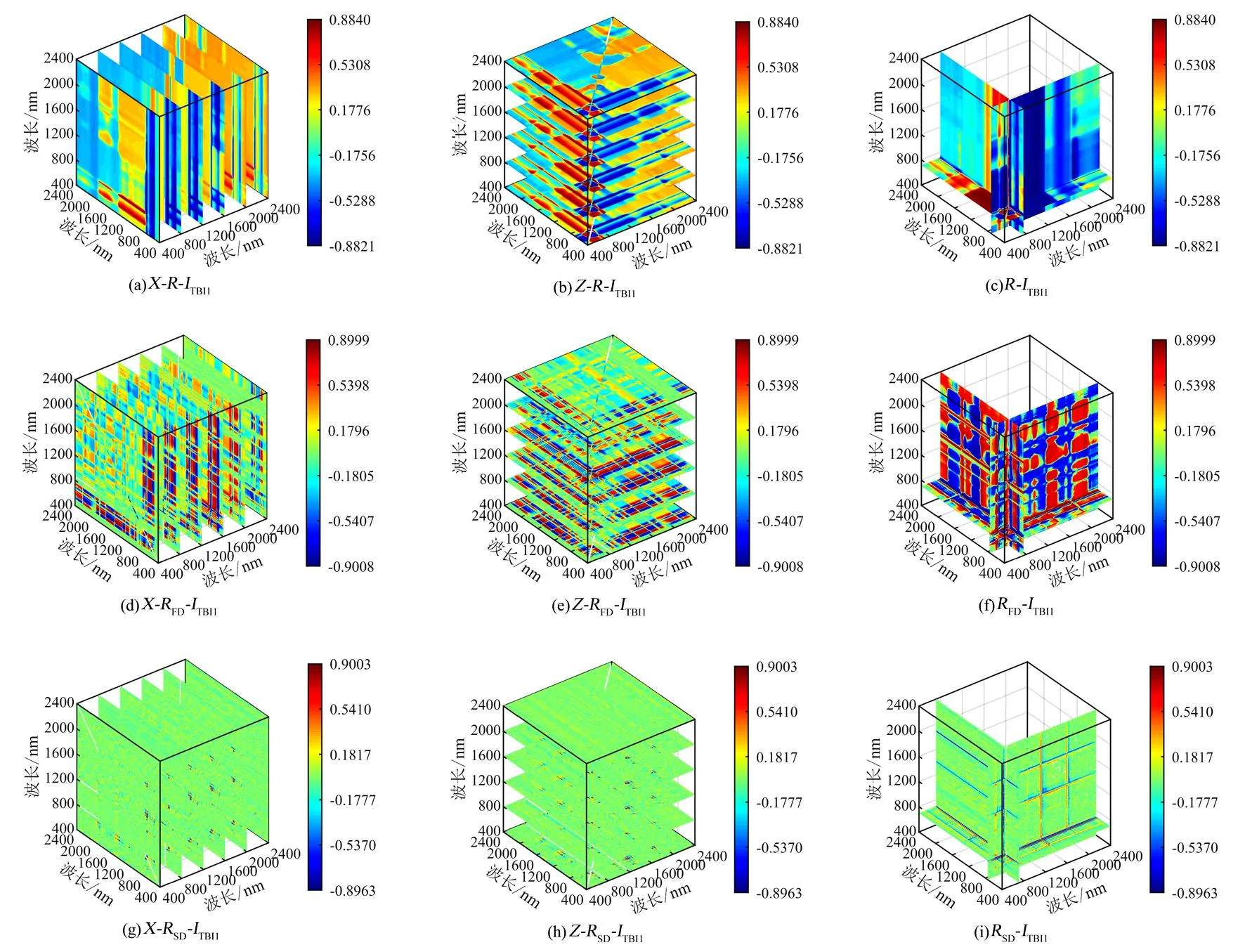
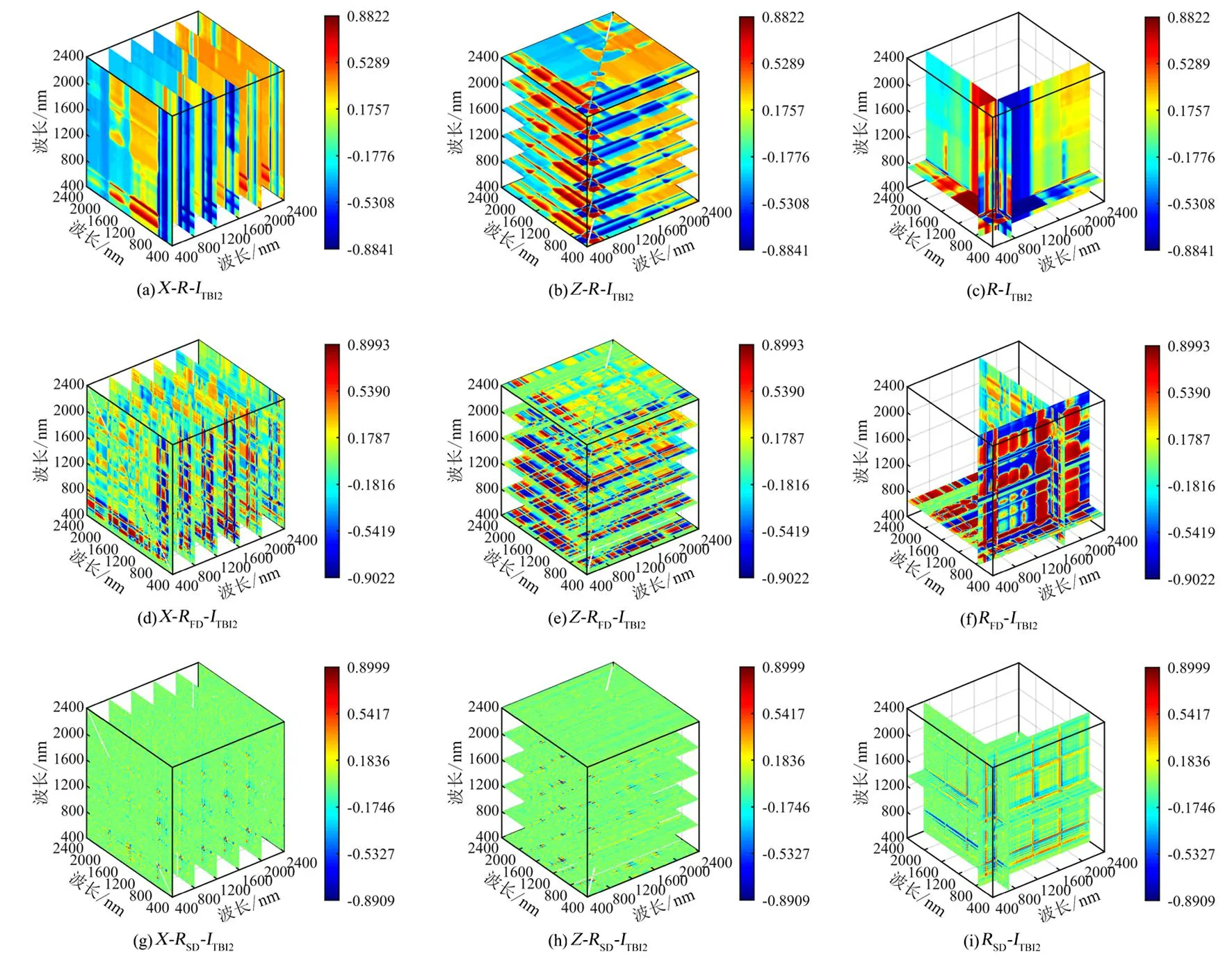
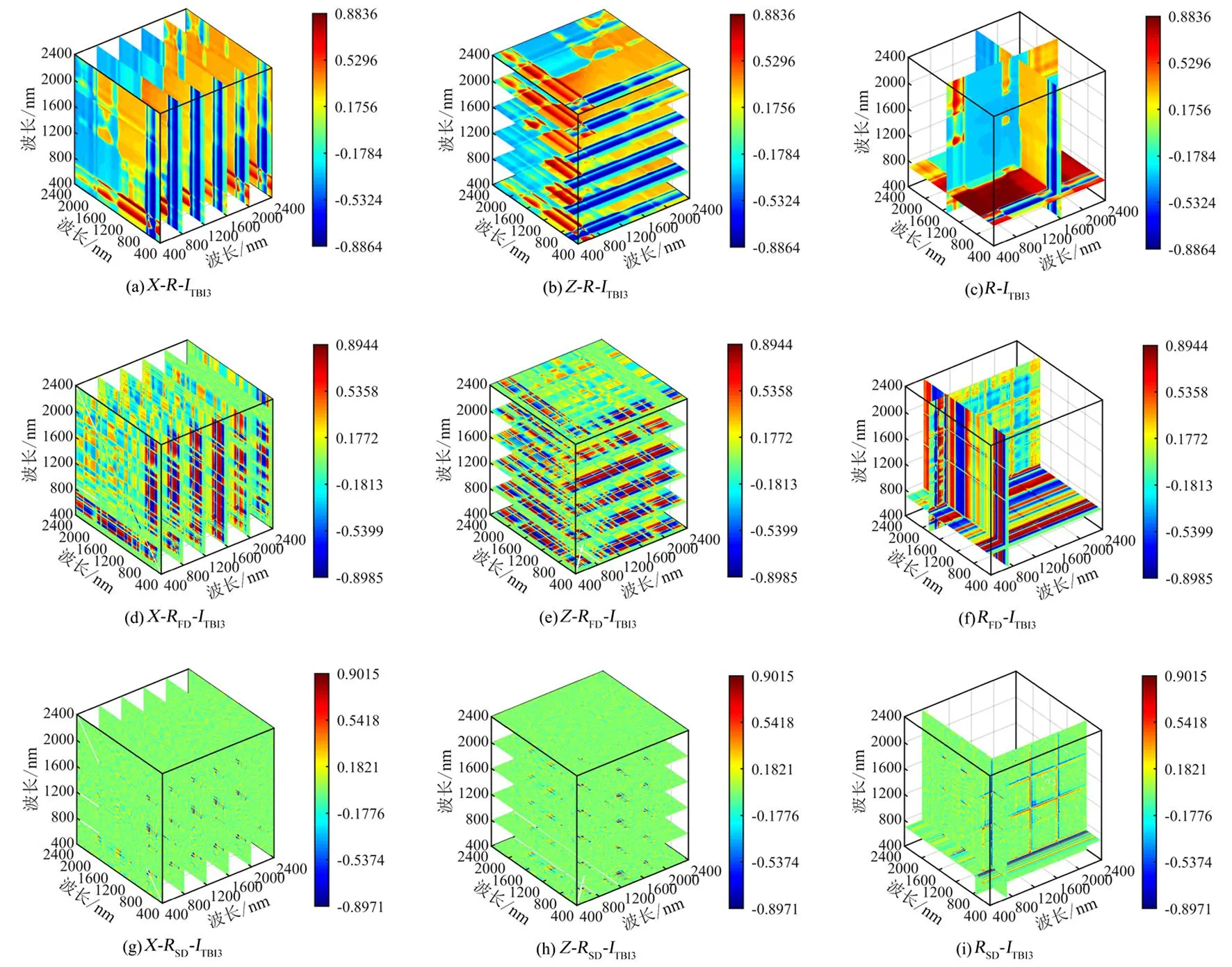
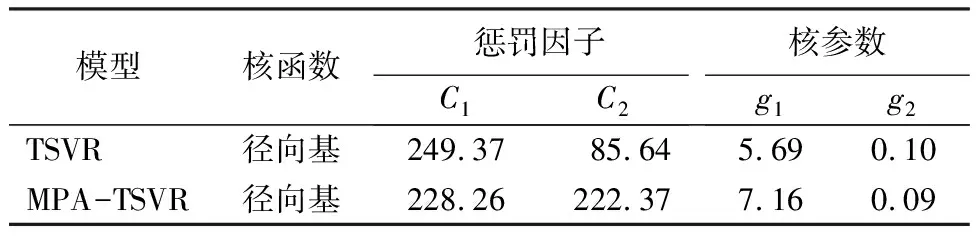
TSVR的惩罚因子C1、C2和核参数g1、g2对模型预测精度影响较大。用MPA对TSVR中C1、C2和g1、g2进行优化,以训练集的均方根误差(RMSE)为适应度函数,循环迭代计算个体适应度值,直到找到满足I 图1 MPA-TSVR反演紫丁香叶片叶绿素面密度流程图 (3)模型评价指标 选择决定系数(R2)和均方根误差(RMSE)作为模型精度评价指标[21],R2越趋近于1,RMSE越趋近于0,模型预测精度越高、稳定性越强、整体效果越好。 紫丁香叶片原始(R)和预处理(RFD、RSD)后的160条光谱曲线如图2所示。R在700、1 400和1 900 nm处有明显的吸收谷,其中700 nm处的吸收谷与叶绿素面密度有关。相比R,经RFD处理后的光谱曲线在一定程度上消除了基线漂移,凸显R的部分肩峰,但在凸显特征峰的同时噪音也有所增加。经RSD处理后的光谱曲线,反射率值明显减小,特征峰和噪音较RFD更为明显。说明利用微分求导预处理光谱,在增强光谱特征的同时也会增强噪音。 图2 原始光谱和预处理后光谱 2.2.1 一维光谱指数与叶绿素面密度的相关性 一维光谱指数与紫丁香叶片叶绿素面密度相关系数矩阵图如图3所示,rmax达到0.874 0。不同光谱反射率与叶绿素面密度之间的敏感波长主要集中在500~650 nm以及700~800 nm区间,不同预处理下光谱反射率与叶绿素面密度间的rmax均在0.8以上。经RFD处理之后,叶绿素面密度敏感波段范围缩小,敏感波长更为精准,叶绿素面密度敏感度不高的范围被削弱,而RSD处理后的光谱更加突出此现象,只有几个较强波长的r较高,其余的波长的r都相对较低,甚至接近于零。提取不同预处理下rmax对应的反射率作为最优一维光谱指数用以后续建模,具体见表2。 图3 一维光谱指数与叶绿素面密度相关矩阵 表2 最优光谱指数 2.2.2 二维光谱指数与叶绿素面密度的相关性 二维光谱指数与紫丁香叶片叶绿素面密度相关系数矩阵图如图4所示。不同的预处理方法和不同的二维光谱指数均会对r产生影响。 图4 二维光谱指数与叶绿素面密度相关矩阵 总体来看,与一维光谱指数相比,二维光谱指数的r有所提升,说明二维光谱指数通过波段组合能够加强波段间的相互关系,有效提高光谱信息的利用率。二维光谱指数与一维光谱指数的敏感波长范围基本一致,主要集中在可见光区域,但存在最优光谱指数INDI(RFD744,RFD1399)第2个波长位置在1 399 nm,说明在近红外区也有与叶绿素相关性的信息。不同光谱指数,R构建的二维光谱指数rmax普遍偏低,均小于0.883 5;RFD构建的二维光谱指数rmax均最高,其中RFD-ISRI(图4(e))具有最好的效果,rmax达0.891 1,其次为RSD构建的二维光谱指数,说明RFD和RSD均能有效提高光谱指数与叶绿素面密度之间的r。选取各个矩阵中rmax对应的指数作为最优二维光谱指数用以后续建模,具体见表2。 2.2.3 三维光谱指数与叶绿素面密度的相关性 三维光谱指数与紫丁香叶片叶绿素面密度相关系数矩阵图如图5~7所示。不同的预处理方法和不同的三维光谱指数均会对r产生影响。三维光谱指数的rmax均高于0.882 2,比同一预处理下一维和二维光谱指数高,说明将组成指数的波长扩展至3个能够将更多的光谱信息提取出来,对提升叶绿素面密度的敏感度具有一定作用。R处理下的不同三维光谱指数rmax均最低,不同于最优预处理为RFD的一维和二维光谱指数,RSD是构建三维光谱指数的最优预处理方法,其中RSD-ITBI3(图7中的(g)、(h)、(i))的rmax最高,达0.901 5,说明三维光谱指数有利于降低RSD预处理在凸显特征时所产生的噪音,能够有效提高特征筛选的灵敏度。 图5 三维光谱指数ITBI1与叶绿素面密度相关矩阵 图6 三维光谱指数ITBI2与叶绿素面密度相关矩阵 图7 三维光谱指数ITBI3与叶绿素面密度相关矩阵 研究发现,三维光谱指数ITBI1(图5)构建的最优指数均在可见光(700~750 nm)范围内;ITBI2和ITBI3中,除了R-ITBI2和RSD-ITBI3,每个指数中至少有1个波长靠近1 450 nm,结合二维光谱指数来看,说明近红外区存在与叶绿素面密度相关的信息。选取各个矩阵中rmax对应的指数作为最优三维光谱指数用以后续建模,具体见表2。 经PCC筛选出的最优光谱指数如表2所示。将不同预处理及不同维度下的最优光谱指数作为输入参数,分别用TSVR和MPA-TSVR对紫丁香叶片叶绿素面密度进行反演。 不同预处理下最优光谱指数分别建立TSVR和MPA-TSVR紫丁香叶片叶绿素面密度反演模型,结果见表3。MPA-TSVR构建的紫丁香叶片叶绿素面密度反演模型精度均高于TSVR。同一建模方法,不同预处理下构建模型的精度由高到低顺序为RSD、RFD、R,说明对R进行预处理是有必要的,RSD是最佳预处理方法,RSD-MPA-TSVR精度最高,测试集R2为0.906 0,RMSE为3.882 7。使用PCC筛选得到的RFD最优光谱指数比RSD最优光谱指数rmax高,而建模结果显示RSD是最佳预处理方法,说明非线性模型的r和R2之间没有必然联系。因此在构建非线性模型时,输入参数的好坏不能用r进行评价,而要对预处理方法和所构建的光谱指数进行排列组合,对比模型预测精度才能确定最佳输入参数。 表3 不同预处理下最优光谱指数构建TSVR和MPA-TSVR模型反演叶绿素面密度结果 不同维度下最优光谱指数分别建立TSVR和MPA-TSVR紫丁香叶片叶绿素面密度反演模型,结果见表4。不同输入参数,同样是MPA-TSVR模型精度高于TSVR,可以看出不论输入参数如何变化,MPA-TSVR模型精度均高于TSVR,说明MPA优化算法能够找到TSVR中惩罚参数和核参数的最优值,避免TSVR在运算过程中陷入局部最优。同一建模方法,不同维度构建模型精度由高到低顺序为:三维、二维、一维,说明光谱指数维度增加,其对叶绿素面密度的响应度也会增加。二维光谱指数中,INDI-MPA-TSVR精度最高,测试集R2为0.882 0,RMSE为4.350 2;三维光谱指数中,ITBI3-MPA-TSVR精度最高,测试集R2为0.911 0,RMSE为3.776 3。 表4 不同维度下最优光谱指数构建TSVR和MPA-TSVR反演叶绿素面密度结果 综合所有模型来看,ITBI3为最优输入参数,其构建的TSVR和MPA-TSVR模型参数对比如表5所示。 表5 TSVR初始参数与MPA-TSVR优化参数 用最优输入参数ITBI3分别构建PLSR、BPNN和SVR模型。其中,PLSR主成分数为2,ITBI3-PLSR测试集R2为0.897 1,RMSE为4.061 8;BPNN隐含层节点数设置为7,ITBI3-BPNN测试集R2为0.899 6,RMSE为4.012 9;SVR选用径向基核函数,惩罚参数C和核函数g分别为210和2-6,ITBI3-SVR测试集R2为0.901 7,RMSE为3.970 8,精度均低于ITBI3-MPA-TSVR。不同模型反演紫丁香叶片叶绿素面密度预测值与实测值的对比如图8所示。ITBI3-MPA-TSVR预测值与实测值的散点较其他模型更靠近Y-预测值=Y这条直线,预测精度更高。因此,ITBI3-MPA-TSVR对叶绿素面密度的预测能力、拟合程度和准确性均优于本研究中所有模型。 图8 不同模型反演紫丁香叶片叶绿素面密度测试集预测结果 本研究以内蒙古农业大学东校区内紫丁香为研究对象,采集160个样品的光谱数据和对应的叶片叶绿素面密度,在一维和二维光谱指数的基础上,首次在叶绿素面密度预测方面引入三维光谱指数,构建了基于R、RFD和RSD光谱400~2 400 nm范围内任意波长下不同维度的光谱指数。用PCC分析了光谱指数与叶绿素面密度间的相关性,并筛选出最优光谱指数。首次将MPA-TSVR模型引入植物生理指标预测研究,构建了基于不同预处理和不同维度下的最优指数和MPA-TSVR紫丁香叶片叶绿素面密度预测模型,最优输入参数分别建立PLSR、BPNN和SVR预测模型,优选出最佳紫丁香叶片叶绿素面密度预测模型,得出以下结论: (1)最优光谱指数中,一维光谱指数RFD744、二维光谱指数ISRI(RFD704,RFD738)和三维光谱指数ITBI3(RSD714,RSD745,RSD700)的r最大,分别为0.874 0和0.891 1为0.901 5,不同预处理,基于RFD构建的一维和二维光谱指数与叶绿素面密度相关性最高,RSD构建的三维光谱指数与叶绿素面密度相关性最高;不同维度,三维光谱指数相比于一维和二维光谱指数对叶绿素面密度更加敏感。 (2)同一建模方法,不同预处理下最优光谱指数建模精度由高到低的顺序为RSD、RFD、R。基于RSD-MPA-TSVR构建的叶绿素面密度反演模型具有最佳预测效果,其R2可达0.906 0,RMSE仅有3.882 7;同一预处理方法,不同维度最优光谱指数建模精度由高到低的顺序为:三维、二维、一维。二维光谱指数中,INDI-MPA-TSVR反演效果最好,测试集R2为0.882 0,RMSE为4.350 2;三维光谱指数中,ITBI3-MPA-TSVR反演效果最好,测试集R2为0.911 0,RMSE为3.776 3。不论输入参数如何,MPA-TSVR的建模精度均高于TSVR。 (3)对于紫丁香叶片叶绿素面密度反演模型而言,MPA-TSVR相比于PLSR、BPNN和SVR模型更稳定。ITBI3-MPA-TSVR是紫丁香叶片叶绿素面密度最优反演模型。本研究光谱采集未在活体上进行,是为同步叶绿素面密度测定,减少误差。后续光谱数据可在活体采集,通过构建光谱指数输入ITBI3-MPA-TSVR模型即可实现叶绿素面密度的无损检测。 通过ITBI3-MPA-TSVR实现了紫丁香叶片叶绿素面密度的反演,三维光谱指数和MPA-TSVR模型的应用对城市绿化植物其他生化组分的定量预测具有一定的参考价值。全波段构建三维光谱指数既减少了光谱无关信息,又因其在二维光谱指数的基础上增加第3个波段,提升了信息的包含度,能够很大程度上突出特征信息。但是由于光谱信息十分复杂,预处理方法和光谱指数的选择在很大程度上影响光谱指数对叶绿素面密度的响应,最优光谱指数的筛选方法直接对模型精度产生影响。因此,对预处理方法、光谱指数以及最优光谱指数筛选方法的选择有待进一步研究。
2 结果与分析
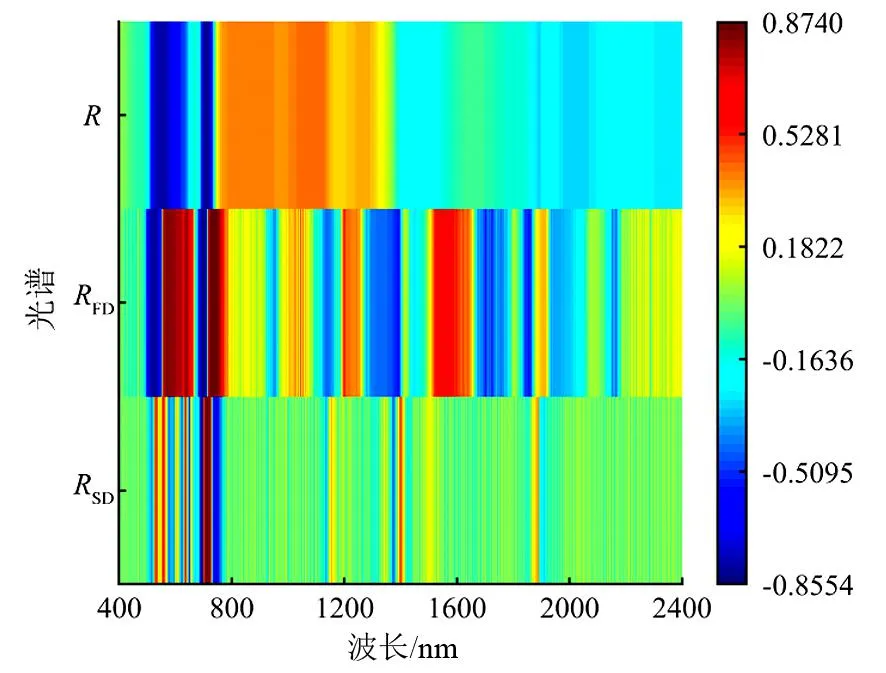
2.1 叶片光谱预处理结果

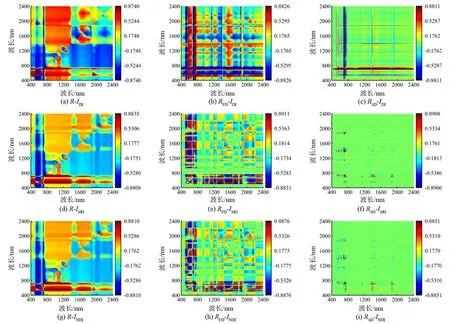
2.2 光谱指数PCC分析及最优光谱指数

2.3 模型预测结果



3 结论

