小学数学教学中数形结合思想的渗透

文｜康长华

数学是一门既抽象又具体的学科，引入数形结合思想，能将抽象的数学概念与具体的图形相结合，通过直观的图形帮助学生理解和掌握数学知识，对学生的数学学习产生积极影响。

一、以形助思，培养学生的数学思维能力

数学概念是课程学习的基础，在“分数的初步认识”课程教学中，对于“分数”概念的讲解，教师可以利用圆形或正方形的模型，将分数概念具化为实际的物体，帮助学生形成分数的视觉化认知。

第一步，引导学生回忆已学过的整数知识，带领学生回顾整数的基数、大小比较等知识点，为认识、理解分数做好基础知识铺垫，将整数知识和分数知识联系，建立更完整的知识体系。

第二步，引入分数概念引导学生回忆整数的基数概念，让学生感知分数的基数可以看作是整体的“部分”数量，使学生比较容易理解分数的概念和意义，促进对分数的理解。

第三步，将模型分发给学生，让学生用标记笔将其平均分成4 份，其中的一份就表示，学生观察模型布局，教师拿出其中个圆形模型并顺势引入分数的概念，写出，并解释它的含义。第四步，展示不同形状的，如圆形、正方形、长方形等，帮助学生理解分数的普遍性，在学生对分数有了初步认识后，教师可以进一步深化学生对分数的理解，帮助学生更深入地理解分数的概念，明白分数的实际应用。

教师可以利用图形比较概念。对于一些相似的数学概念，教师可以利用图形进行比较，帮助学生区分它们的异同点。例如，学生在学习“图形的运动”课程中容易对“轴对称”和“中心对称”两个概念混淆，教师可以利用一个轴对称图形和一个中心对称图形进行比较，让学生更清晰地理解它们的区别。

第一步，准备一些轴对称图形和中心对称图形的折纸进行示例，教师展示一个正方形（轴对称），一个圆形（中心对称），将正方形沿着一条对角线对折，让学生观察折纸后的图形，并让学生思考这个图形沿对称轴折叠后直线两旁的部分是否重合。

第二步，把一个圆形沿着一条直径对折，让学生观察折纸后的图形，并让学生思考这个图形绕对称中心旋转180°后，前后图形是否重合。

第三步，在展示和折纸实验之后，教师可以引导学生比较这两个图形的异同点，轴对称图形沿对称轴折叠后两侧图形能够完全重合，而中心对称图形绕对称中心旋转180°后，前后图形能够完全重合。借助具体的图形展示助推学生对知识、概念的理解，帮助学生建立数学知识直观化的意识，培养数学思维能力，学生可以更清晰地区分“轴对称”和“中心对称”的概念，并通过图形比较进一步加深对它们异同点的理解，也能提高学生的辨别能力和独立思考能力。

通过图形可以深化学生对数学概念的理解，以形助思的方式，将数学问题中的文字描述、数量关系灵活地转化为简单、直观化的图形，帮助学生更好地理解题意，从而更快地找到解题思路和方法，培养学生的数学思维能力、发散思维能力和解决问题的能力，有效地提高教学质量和数学课堂的学习效果。

二、以形推数，提高学生的解题能力

图形具有直观性，能够将抽象的数学问题转化为具体的图形问题，使学生更容易理解题目中的信息和问题，通过画图等方式可以帮助学生更好地理解题意，找到问题的突破口。通过将图形与数学问题相互转化，可以帮助学生更好地掌握解题方法，提高解题能力。教师可以让学生用图形化工具（如数位图、方格图等）来验证自己的答案，从而提高解题的准确性。

例如，在“图形的运动（二）”教学中，为了让学生了解平移、旋转、翻折等图形的基本运动方式，教师可以让学生观察和操作图形，预测和描述它们在运动中的变化，进而培养学生的观察、推理和解决问题的能力。教师在课前需要准备教学工具：（1）多个图形模型，如正方形、矩形、圆形等。（2）准备平移、旋转、翻折等图形运动的练习题和相关教具，如透明纸、图形卡片等。实施教学的过程中，教师可以展示一个图形，并问学生这个图形有什么特点，引导学生讨论图形的运动方式。再出示一个正方形模型，让学生通过手动操作将其平移，教师引导学生观察并描述图形在平移过程中位置的变化。接着，出示其他不同形状的图形模型，如矩形、圆形等，让学生进行平移操作，并观察、描述图形的位置变化。学生对“平移”有了基础认识后，教师可以让学生动手操作正方形模型，将其旋转，引导学生观察并描述图形在旋转过程中的变化。教师分发其他不同形状的图形模型，让学生进行旋转操作，并观察、描述图形的变化特点。

在此基础上，教师给出练习题“将图形A 按照规定的运动方式移动到图形B 的位置”，提供一些实际生活中的情境问题，如“小明把一个长方形蛋糕切成正方形块，请你观察这些块在移动过程中会发生什么变化”，根据所学的平移、旋转等运动规则，引导学生通过观察图形的形状和位置变化，运用推理来回答问题。学生可以通过实际操作和观察图形的变化，深入理解图形的运动方式，培养学生对图形变化的直观感知能力，提高学生解决与图形运动相关问题的能力。

三、数形相融，强化学生自主学习意识

小学生处于形象思维为主的阶段，对抽象的数学概念和算法的理解存在一定的困难，并且自主学习能力较弱，缺乏独立思考和解决问题的能力。教师将抽象的数学问题转化为形象生动的图形和动画，符合小学生的认知特点，能激发学生的学习兴趣，从而提高学生的自主学习能力。

“鸡兔同笼”是典型的数学题目，在《孙子算经》里，鸡兔同笼问题被叫作雉兔同笼问题，原文为：今有雉、兔同笼，上有三十五头，下有九十四足。问：雉、兔各几何？鸡兔同笼的解决方法非常多，这一课程的学习需要通过假设、利用想象来求解，能更好地训练学生的思维能力与自主探索能力。在引导学生解决一些涉及数量关系的数学问题时，教师可以借助直观图形，帮助学生理解题意。将问题中的文字转化为图形，以便更好地理解题意，如解决关于相遇问题、追及问题等应用题时，教师可以让学生用线段图来显示题目中的数量关系，帮助学生清晰地理解问题。应用数形结合思想教学，学生可以从图形的转换中发现其中的解题规律，拓展不同的解题思路。在教学中采用线段图的方法来引导学生解决问题，教师先用线段表示鸡和兔，空白的线段代表鸡的只数，阴影线段代表兔的只数。

图1

已知，一只鸡2 只脚，一只兔子4 只脚，在上图的基础上，向外拓展一下，形成下面的图形：

图2

可见，空白区域的面积等于鸡×2，即鸡的脚数，阴影区域的面积等于兔×4，即兔子的脚数。这里有一个条件：鸡和兔子的数量一共是35 只，教师可以引导学生构建出下面的图形：

图3

从上图可以计算出35×4=140，是整个图形的面积，从上面的分析中可以知道，多出来的阴影部分面积等于140-94=46，而这个长方形的宽=4-2=2，那么长就应该等于46÷2=23，也就是鸡的数量，进而得出兔子的数量是35-23=12 只。

这种方法不仅计算快，还为学生拓宽了求解鸡兔同笼问题的视野，从呆板单一的数字运算中，轻松地过渡到图形的世界之中，对于启发学生的数形结合思想，激发学生的创造力非常有帮助。这一课程对三年级学生来说，如果按照课本的知识点来讲解，部分学生能够听懂，但是用面积的方法来讲，更容易看懂，这种方法利用了数形结合思想，实质是面积概念中的“积”的应用，所谓的积就是两个数相乘，从算式来看，就是35×4，从图形来看，就是长35，宽4 的一个长方形的图形面积，学生可以用图形的面积来代表两个数的乘积，让学生亲身体验鸡兔同笼问题的解法，解决问题的同时调动学生的探究积极性，使学生能够自主地进行反思，拓展更多的解题思路和方法，从而让学生养成自主探究、主动学习的习惯。

四、以图为引，巩固学生数学知识应用能力

教师可以将数形结合教学模式应用于课堂作业设计，借助图形元素，学生可以更快地找到解题思路，提高解题速度和效率，并且可以激发学生的学习兴趣和动力。通过观察和分析学生的解题过程，教师可以更好地了解学生的学习特点和问题，并及时进行反馈与调整。以“图形的运动（二）”为例，引导学生感知平移，在观察图形、具体操作图形的过程中，理解平移的特点，发展空间观念，具体设计如下。

（一）画一画

1.画出左图的另一半，使其成为轴对称图形。

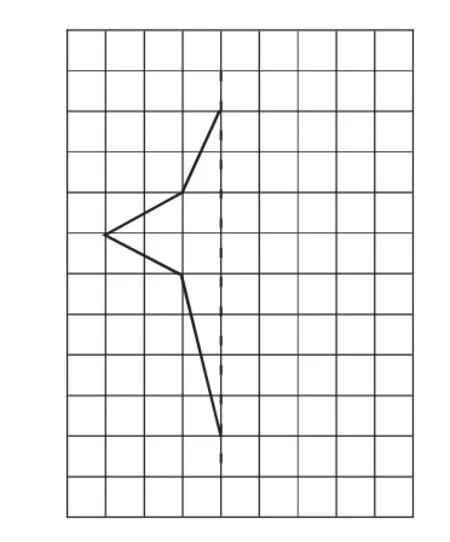
图4

2.先画出小树向上平移6 格后的图形。再画出继续向右平移12 格后的图形。

图5

本部分是预习作业，能调动学生已有的知识储备，唤醒学生已有的学习经验，为新课学习铺路搭桥，通过课前作业的反馈，教师能分析、了解学生的学情，找准学生的新知生长点。

（二）拼一拼，算一算

假设我们有一个长为4 cm，宽为3 cm 的长方形木板，如下图所示，现在我们需要将其分割成若干个1 cm×1 cm 的小正方形。

Ѳ问题：（1）这个长方形木板可以分割成多少个小正方形？（2）如果我们将其中的一部分小正方形拼成一个新的长方形，新长方形的面积是多少？

图6

Ѳ解题分析：根据长方形木板的尺寸，可以计算出其面积是4×3=12 cm2。由于每个小正方形的面积为1 cm2，因此这个长方形木板可以分割成12 个小正方形。如果将其中一部分小正方形拼成一个新的长方形，那么这个新长方形的面积一定是12 的因数。

本题方法多样，让学生自己动手实践，给予学生开拓创新的空间。

综上所述，数形结合思想通过将数学概念与几何图形相结合，以图形形式展示数学问题，以增加学生对数学知识的理解和应用能力。教师在应用过程中，需要充分发挥引导和激发学生学习兴趣的作用，营造积极的学习氛围，组织学生进行解决问题、发散思维等活动，培养学生的数学思维能力和创造力，以提高小学数学课堂教学效率。