以思维工具助力“问思式”数学课堂构建，提升学生学习力——以“垂直与平行”一课为例

文｜洪亚明

思维工具是数学教学中的得力助手，教师借助思维工具能够将抽象化的知识具象化，将碎片化的内容联系起来，从而帮助学生更好地掌握数学概念。以思维工具来构建“问思式”课堂，能够让学生在问题中思考，思考后再提出问题，直至最后无惑为止，这是提升学生学习力的有效手段。

“问思式”课堂教学是通过引导学生自主学习，积极思考，形成自己的思维成果。教学中，教师要借助思维工具助力构建“问思式”课堂，培养学生的学科素养。教师可以通过问题、情境、活动三种方式激发学生思维；借助思维工具，设计思维导图，引导学生的思维从具体到抽象转变；采用思维导图法和活动法两种方法创设课堂情境，培养学生的创新能力。

一、以思维工具助力构建“问思式”课堂的教学意义

《义务教育数学课程标准（2022 年版）》指出：“在小学数学教学中，要创设有利于激发和培养创新精神和实践能力的学习情境，让学生亲身经历知识形成过程、巩固和应用过程以及知识、技能和方法的类化过程，从而使学生学会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”。结合课标核心素养，数学“问思式”课堂教学的基本环节为“问—思—导—辨—总—行”，其中问、思、导、辨是四个关键环节。

【问】在课堂教学过程中，教师应始终围绕一个问题或一个核心问题，有目的、有计划地引导学生进行提问，激发学生的思维。

【思】教师引导学生进行知识建构，引导学生发现数学规律、思维方法和数学思想方法，形成数学核心素养。

【导】在课堂教学中，教师要让学生主动地参与学习过程，引导他们通过观察、实验、猜想、验证、推理等形式来探索知识的本质特征和规律。

【辨】教师引导学生分析和比较各种方法的优缺点，并进一步总结归纳出一些新的思想、结论或者规律，进一步发展学生的创造性思维。

【总】教师结合总结的知识技能和数学思想方法等来指导学生下一步学习。

【行】行动、实践，教师引导学生把学到的知识不断地加以应用。

构建“问思式”课堂，巧用思维工具是其最重要的特征，这就要求教师在进行教学设计时要做到：以问题为中心构建课堂结构；以思维工具为助手进行课堂教学；以学生思维发展规律和特点为依据整合课程内容。

因此，我们需要对思维工具的使用有一个清晰的认识，这将有利于指导学生有效地进行问题思考和解答。常见的思维工具有“双气泡图”“流程图”“大括号图”等多种形式，具有不一样的引导作用。教师巧用思维工具，可以帮助学生更好地解决问题。

二、借助思维工具构建“问思式”课堂教学策略

在小学数学课堂中开展“问思式”课堂教学是新课程改革的必然要求，它能促进学生在学习过程中养成主动积极思考的习惯，提高学生分析问题和解决问题的能力。我发现在小学数学课堂上开展“问思式”教学可以发挥思维工具的作用，助力提高学生的数学核心素养。因此，我将以“垂直与平行”一课为例，利用思维工具进行“问思式”教学的案例研究。

（一）运用思维工具来开展问题导学，培养学生的自主学习能力

“问思式”课堂中的核心在于问题，有问题学生才会去探究，通过探究才能得到知识的扩充和学习力的提升。教师在开展小学数学教学的过程中，应善于从教材中寻找问题，从教学中发掘问题的切入点，以恰当的时机和正确的提问方式来开展问题导学，从而让学生能够有自主探究、自主学习的时间和空间。

一般而言，课堂刚开始时的导入环节是应用思维工具的最佳时期，在这个环节中，学生的学习热情得以调动，学生对于未知的知识会有一定的好奇心，教师此时以气泡图为核心，让学生对某一个概念或者定理进行知识的填充，从而引导学生预习课本，也给了学生思考的机会，让学生的主体性得以体现。

本课片段：小组合作，初步探究两条直线的位置关系

1.（课件出示）导学目标（一）

（1）自主想象两条直线的位置关系。

（2）实践探究：在纸上任意画两条直线。

（3）小组交流：你画的两条直线的位置关系是怎样的？在图1 中呈现出来：

图1

2.教师巡视，选取学生作品

气泡图法具有独特的优势，它可以帮助学生从整体上把握问题，同时可以直观地发现问题、解决问题，是一种高效的思维方法。教学中教师在应用气泡图进行问题导学时，可以先为学生确定本次教学的中心概念，再从这个概念引申出问题，将问题放置于气泡图之中，以此来引导学生思考探究，让学生通过自己的探索得出结果，从而帮助学生更好地认识概念的本质，也让学生的记忆更加深刻。教师利用气泡图可以激发学生的空间想象力，画出两条直线各种可能的位置关系。

（二）运用思维工具组织合作探究，开拓学生的数学思维能力

数学知识具有一定的联系性，学生已经在过去的学习中掌握了基本的数学概念，也有了一定的数学思维和数学基础，教师要做的就是将所有的知识进行串联，让学生发现知识之间的联系，从而构建出一定的知识结构，使数学学习变得更系统化。借助思维工具开展“问思式”课堂时，教师可以以关键词为核心，再组织学生进行小组合作探究，画出一个完整的思维导图，鼓励学生进行思考、探究，拓展学生的数学思维，让学生在合作中成长，从多角度思考问题，形成一定的知识迁移。

分类要求：先自己思考应该怎样分类，然后在小组中交流，说说你是按什么来分的。

如用树状图分类呈现“两条直线的位置关系”的知识脉络（见图2）：

图2

教师首先给出思维导图的主图“两条直线的位置关系”，再为学生画出下面的分支，让学生在此基础上补充内容。教师鼓励学生通过合作将各种可能的位置关系都罗列出来，根据两条直线存在“相交”与“不相交”两种情况，再分类匹配到各自的树状图里。通过这个过程，学生的思维得到了开拓，而思维导图的绘制让学生的思维更具条理性，学生能够对两条直线的位置关系形成系统性的认知，从而在应用数学知识时也会更加高效。

（三）运用思维工具布置学习任务单，提升学生掌握知识的能力

教师在构建“问思式”课堂的过程中，也可以给学生提供一个“大括号图”，以学习单的形式发布给学生，让学生能够在学习任务单的指导下，有条不紊地进行自学和自我完善，并能够完成教师给予的问题和任务，得到最终的学习成果。在学习任务单的帮助下，学生的学习力能够得到锻炼，学生所掌握的知识也会更为牢固。

1.自学知识，明确平行和垂直的含义

片段例析：

（1）课件出示导学目标（二）

请认真看书65 页，并回答下面问题：

①什么叫平行线？

②什么情况下两条直线互相平行？

学后反馈，教学平行。

（2）课件出示导学目标（三）

请认真看书65 页，并回答下面问题：

①什么叫垂直线？

②什么情况下两条直线互相垂直？

2.学后反馈，巩固教学

我先出示一个长方体盒，让学生观察这个长方体盒有多少个面，然后，我再拿出一根红色和一根绿色的小棒。我先把两根小棒放在同一平面内，问：“它们在同一平面内吗？”然后，我把红色的一根小棒放在另一个平面，问：“它们还在同一平面内吗？”

小结：两条直线互相平行、互相垂直必须具备一些什么条件？（见图3）

图3

教师在以思维工具中的“大括号图”为引，进行学习任务单的设计时，确定任务单的问题既是关键词，也是精髓所在。教师再根据问题核心进行学习步骤的细化，让学生的探究学习能够走到正确的方向。通过这样的任务学习单，学生的学习步骤有了科学的指导，学生也能够根据“大括号图”的指引慢慢地完成探究，在完成的过程中得到综合锻炼，从而提升学习力。

（四）运用思维工具优化分类方法，辨别垂直与平行的特征

片段例析：动手操作，感知垂直

教师引导学生动手折出垂线。（把一张正方形纸折两次，使两条折痕互相垂直。最简捷的方法是沿边长或对角线对折），如图4 所示：

图4（1）

在课堂教学中，教师以思维工具中的双气泡图（见图5）为引，根据两条直线的位置关系，引导学生通过对比、分析、归纳、总结，辨别两条直线间是否垂直或平行，从而培养学生的分类对比意识。

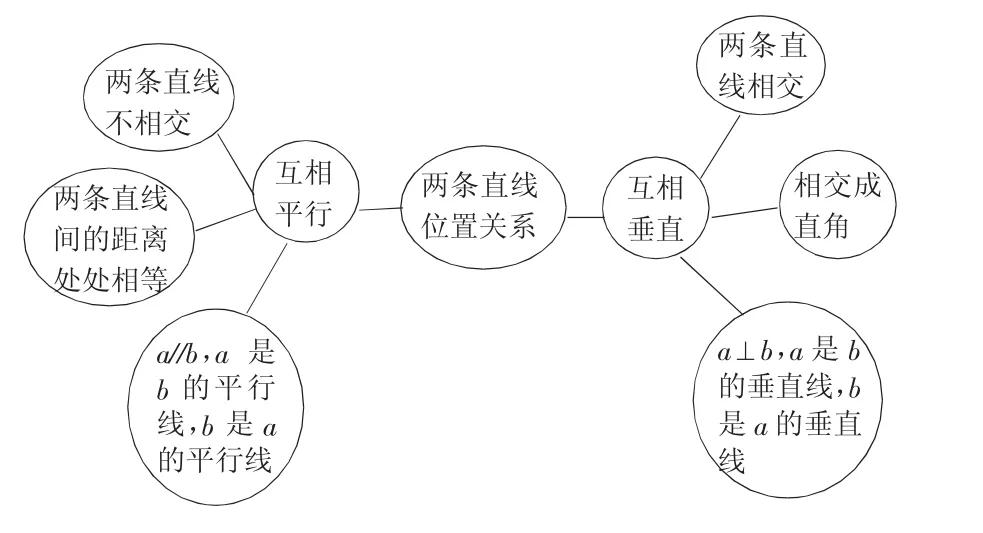
图5

三、结语

综上所述，教师在运用思维工具构建“问思式”课堂的过程中，应当注意到思与学的关系，并能够进行针对性的教学设计，让学生从提问中思考，从思考中进行深度学习。教师借助思维工具开展高效教学，可以让学生在课堂上不断解决疑惑，并能够逐渐地深入学习并掌握数学概念，从而激发学生的学习热情，提升学生的学习力。