例析立体几何中的四种图形变换

赵荣华

(吉林省四平市教育学院)

立体几何的研究对象是空间几何体,在研究空间几何的有关问题时,我们经常要对它的图形进行一些变换,如展开、折叠、割补、还原等.本文举例说明.

1 折叠变换

将平面图形按照一定的要求进行折叠,得到空间几何体,研究几何体的性质,或计算几何体的体积与表面积是一种常见的题型.解决这类问题的关键是要分清折叠前后位置关系和数量关系中的变与不变.

例1 如图1所示,在直角梯形ABCD中,AB//DC,∠BAD＝90°,AB＝4,AD＝2,DC＝3,点E在CD上,且DE＝2,将△ADE沿AE折起,使得平面ADE⊥平面ABCE,G为AE的中点.

图1

(1)求证:DG⊥平面ABCE;

(2)求四棱锥D-ABCE的体积;

(3)在线段BD上是否存在点P,使得CP//平面ADE? 若存在,求的值;若不存在,请说明理由.

(1)因为G为AE的中点,AD＝DE＝2,所以DG⊥AE.因为平面ADE⊥平面ABCE,平面ADE∩平面ABCE＝AE,DG⊂平面ADE,所以DG⊥平面ABCE.

(3)如图2所示,过点C作CF//AE交AB于点F,则AF∶FB＝1∶3.过点F作FP//AD交DB于点P,连接PC,则DP∶PB＝1∶3.又CF//AE,AE⊂平面ADE,CF⊄平面ADE,所以CF//平面ADE.

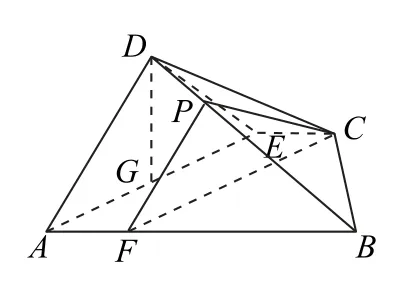
图2

同理,FP//平面ADE.又CF∩PF＝F,CF⊂平 面PFC,PF⊂平面PFC,所以平面PFC//平面ADE.因为CP⊂平面PFC,所以CP//平面ADE,则在BD上存在点P,使得CP//平面ADE,且

本题已经给出图形,解答时只需抓住两个关键点:一是图形翻折前后哪些数量关系和位置关系发生了变化,哪些没有发生变化;二是对照翻折后的图形,按照一般的立体几何问题加以解答.

2 展平变换

将空间图形问题转化为平面图形问题,是解决立体几何问题基本的、常用的方法.将空间图形展开成平面图形后,弄清几何体中相应点和线在展开图中的相应的位置关系是解题的关键.

例2 如图3 所示,已知在圆锥SO中,底面半径r＝1,母线长l＝4,M为母线SA上的一个点,且SM＝x,从点M拉一根绳子,围绕圆锥侧面转到点A,则当绳子最短时,顶点到绳子的最短距离为_________(用x表示).

图3

因为底面半径r＝1,母线长l＝4,所以侧面展开图的弧长为2πr＝2π,则侧面展开扇形的圆心角,因此,将圆锥侧面展开成一个扇形(如图4),从点M拉一绳子围绕圆锥侧面转到点A,最短距离为Rt△ASM1中斜边AM1的长度.因为SM1＝x,SA＝4,所以绳子的最短长度的平方为f(x)＝AM21＝x2＋16(0≤x≤4).设绳子最短时,顶点S到绳子的最短距离等于d,则

图4

本题要求曲面上两点间的最小距离,依据平面上两点之间线段最短的性质将曲面展平成平面,把立体几何问题转化为平面几何问题.立体几何中侧面上两点最短路程问题,一般都采用一个思路.

3 割补变换

对于不规则的几何体,通过“割”或“补”的方法可以将其变为规则的几何体,这就是割补变换法,割补变换常常用于求解体积问题.

例3 图5中的多面体的底面是边长为a的正方形,上面的棱平行于底面,其长为2a,其余的棱长都是a.已知,则这个多面体的体积是________.

图5

如图6所示,在线段PQ上分别取C,C1两点,使得平面ABC⊥平面AA1B1B,平面A1B1C1⊥平面AA1B1B,AB的中点为M,连接CM,则又,所以

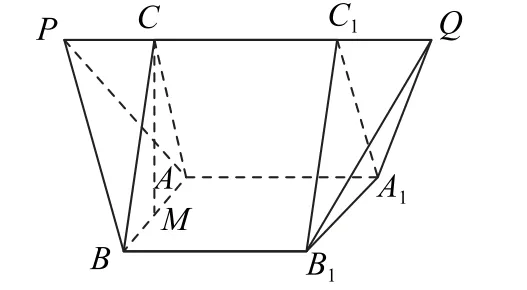
图6

综上,这个多面体的体积为

“割”与“补”是解决立体几何问题的常用方法,通过割补变换可化复杂的几何体为已熟知的简单几何体,从而较快地找出解决问题的突破口.本题将多面体分割成三个可求体积的几何体:一个棱柱和两个棱锥.

4 还原变换

有些立体几何问题给出的图形是三视图或空间几何体展开的平面图,解答时往往要将这些图形还原成直观图,最后利用直观图来解决问题.

例4 (多选题)如图7所示,这是一个正方体的展开图,若将它还原为正方体,则以下正确的是( ).

图7

A.AB//CD

B.CD//EF

C.DF//EG

D.HG//EF

由展开图可得几何体的直观图如图8所示,所以AB与CD为异面直线,HG与EF为异面直线,故A 和D 错 误.由 正方体的性质可得DF//EG,DF//CE,DF＝CE,所以四边形CDFE为平行四边形,则EF//CD,故B和C正确.

图8

综上,选BC.

本题考查空间两条直线的位置关系,必须先把平面展开图还原成立体直观图.

折叠、展开、割补和还原是立体几何基本的图形变换,也是高考常考题型.从以上四个例题可以看出,解决这类问题的方法主要有两种:一种是直观想象,借助空间想象来解决问题;另一种是实地实验,通过折纸实验等直观解决问题.

(完)