立体几何解答题中体积的求解策略

马文明

(山东省郯城县美澳学校)

立体几何中空间几何体的体积求解,是高考中的重点与难点,或利用公式直接运算求解,或作为媒介交会知识应用,或创设场景融入实际问题,成为高考中的一个热点问题.涉及立体几何解答题中体积的求解策略主要有两种:

1)利用等体积思维,比如,求三棱锥的体积常用换顶点法;

2)利用化整为零思维,比如,求多面体的体积常用切割法.

1 换顶点法

使用场景:三棱锥体积的求解与应用问题.

第一步:观察三棱锥的4个顶点的情况;

第二步:寻找易求高的顶点的三棱锥,经常利用平行、相似或全等技巧等价转化顶点;

第三步:根据体积公式求得结果.

例1 如图1所示,在三棱柱ABC-A1B1C1中,AB＝AC＝AA1＝3,AB⊥AC,∠A1AB＝∠A1AC,D是棱B1C1的中点.

图1

(1)证明:BC⊥平面A1AD;

(2)若三棱锥B1-A1BD的体积为,求平面A1BD与平面CBB1C1的夹角θ.

(1)如图2所示,取BC的中点O,连接AO,A1O,A1C,CD,因为AB＝AC,所以AO⊥BC.因 为∠A1AB＝∠A1AC,AB＝AC,所 以△A1AB≌△A1AC,则A1B＝A1C,即A1O⊥BC.

图2

因为AO∩A1O＝O,AO⊂平面A1AOD,A1O⊂平面A1AOD,所以BC⊥平面A1AOD,即BC⊥平面A1AD.

(2)如图3所示,连接OD,由(1)可知BC⊥平面AA1DO,因 为BC⊂平 面ABC,且BC⊂平 面BCC1B1,故 平 面AA1DO⊥平 面ABC,平 面AA1DO⊥平面BCC1B1.

图3

过H作HE⊥BD,连接A1E,因为A1H⊥平面BCC1B1,BD⊂平面BCC1B1,所以A1H⊥BD,又因为A1H∩HE＝H,A1H⊂平面A1HE,HE⊂平面A1HE,所以DB⊥平面A1HE.

又A1E⊂平 面A1HE,所 以A1E⊥BD,则∠A1EH即为所求二面角的平面角.在Rt△A1DH

采用换顶点法求解空间几何体的体积,主要是针对三棱锥这一比较常见的几何体,利用换顶点可以转换视角,改变对应图形的底与高之间的相对关系,进而达到巧妙解决问题的目的.

2 切割法

使用场景:多面体体积的求解与应用问题.

第一步:观察空间几何体特征,将多面体切割成其他锥体或进行合理补形;

第二步:分别求出各部分几何体的体积;

第三步:根据切割或组合求解问题.

例2 如图4所示,已知两个四棱锥P1-ABCD与P2-ABCD的公共底面是边长为a的正方形,顶点P1,P2在底面的同侧,棱锥的高P1O1＝P2O2＝h,O1,O2分别为AB,CD的中点,P1D与P2A交于点E,P1C与P2B交于点F.

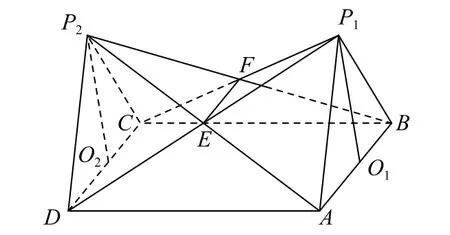
图4

(1)求证:点E为线段P2A的中点;

(2)求这两个棱锥的公共部分的体积.

(1)已知两个四棱锥P1-ABCD与P2-ABCD的公共底面是边长为a的正方形,连接P1P2,O1O2,如图5所示.因为P1O1⊥平面ABCD,P2O2⊥平面ABCD,所以P1O1//P2O2,又P1O1＝P2O2＝h,所以四边形P1O1O2P2是矩形,所以P1P2//O1O2,且P1P2＝O1O2.

图5

又O1,O2分别为AB,CD的中点,所以O1O2//AD,且O1O2＝AD,所 以P1P2//AD,且P1P2＝AD,所以四边形P1P2DA是平行四边形,又P2A∩DP1＝E,所以点E为线段P2A的中点.

(2)连接P2O1交EF于点N,过点P1作P1M⊥P2O1于M,由题意知P2A＝P2B,故P2O1⊥AB.又P1O1⊥AB,P2O1∩P1O1＝O1,P2O1⊂平 面P2P1O1,P1O1⊂平 面P2P1O1,所 以AB⊥平 面P2P1O1,故AB⊥P1M.又P2O1∩AB＝O1,P2O1⊂平面P2AB,AB⊂平面P2AB,所以P1M⊥平面P2AB,即P1M是四棱锥P1-ABFE的高.由(1)同理可得点F为线段P2B的中点,所以

在Rt△P2O2O1中,,则

而P1M＝P1O1sin∠P1O1M＝hcos∠P2O1O2＝,所以

切割法主要用于求解比较复杂或没有特殊规律的空间几何体中的体积问题.通过切割处理,化整为零,或通过补形思想,化缺为整,将不熟悉的几何图形转化为常规且可以利用体积公式来处理的空间几何体问题,进而通过合理的组合来达到解题的目的.

其实,在解决空间几何体的体积问题时,有时可以将一些复杂的、不规则的空间几何体进行必要的转化,如通过切割、组合、拼接、增减等技巧处理,转换视角,变成一个或几个相对规则的空间几何体,进而简单快捷地来求解相应的体积,或借助体积来转化与应用,巧妙化归与转化,快速变形与破解.

(完)