一种液压滑台自适应控制系统的设计与仿真

郑凯

(西安交通工程学院, 机械与电气工程学院, 陕西, 西安 710300)

0 引言

液压滑台被广泛应用在工业与日常生产活动的各个方面,而特殊环境所产生的突变载荷等外部干扰因素影响会造成液压滑台重复定位精度不准确等问题[1]。而作为整个系统的核心部分,其能否对液压系统进行有效控制,直接影响了液压滑台的位置精度,进而对液压滑台的正常工作与运行产生干扰,因此如何进一步提高液压滑台控制系统的稳定性与重复定位精度成为值得研究的问题。本文设计了一种提高液压滑台定位精度的自适应控制系统(以下简称自适应控制系统)。通过将比例反馈环节应用于液压滑台的执行控制系统,提高液压滑台在速度与载荷等特殊条件下的工作精度,扩大液压动力滑台的使用范围与效率。

1 液压滑台总体结构及工作原理

1.1 液压滑台基本结构

本文参照《机械行业标准(JB/T1995-1999)》液压动力滑台的技术条件。液压滑台的核心结构与液压控制系统分别如图1、图2所示。

图1中,1为底座,2为线轨,3为滑台,4为滑块,5为液压缸。

图2中,1为液压源,2为油箱,3为溢流阀,4为电磁换向阀,5为节流阀,6为液压缸。

1.2 工作原理

图2中的SB1按钮接通时,电磁换向阀的线圈(KY1)得电,此时阀芯处于左位,液压油经油口A流入左腔,压力升高并带动活塞杆伸出,当伸出至限位开关(SQ2)时,电磁换向阀4处于中位,活塞杆停止动作。

图2中SB2按钮接通时,电磁换向阀的线圈(KY2)得电,此时阀芯处于右位,液压油经油口B流入右腔,活塞杆退回,当退回至限位开关(SQ1)时,停止动作。其液压滑台的系统原理仿真,如图3所示。

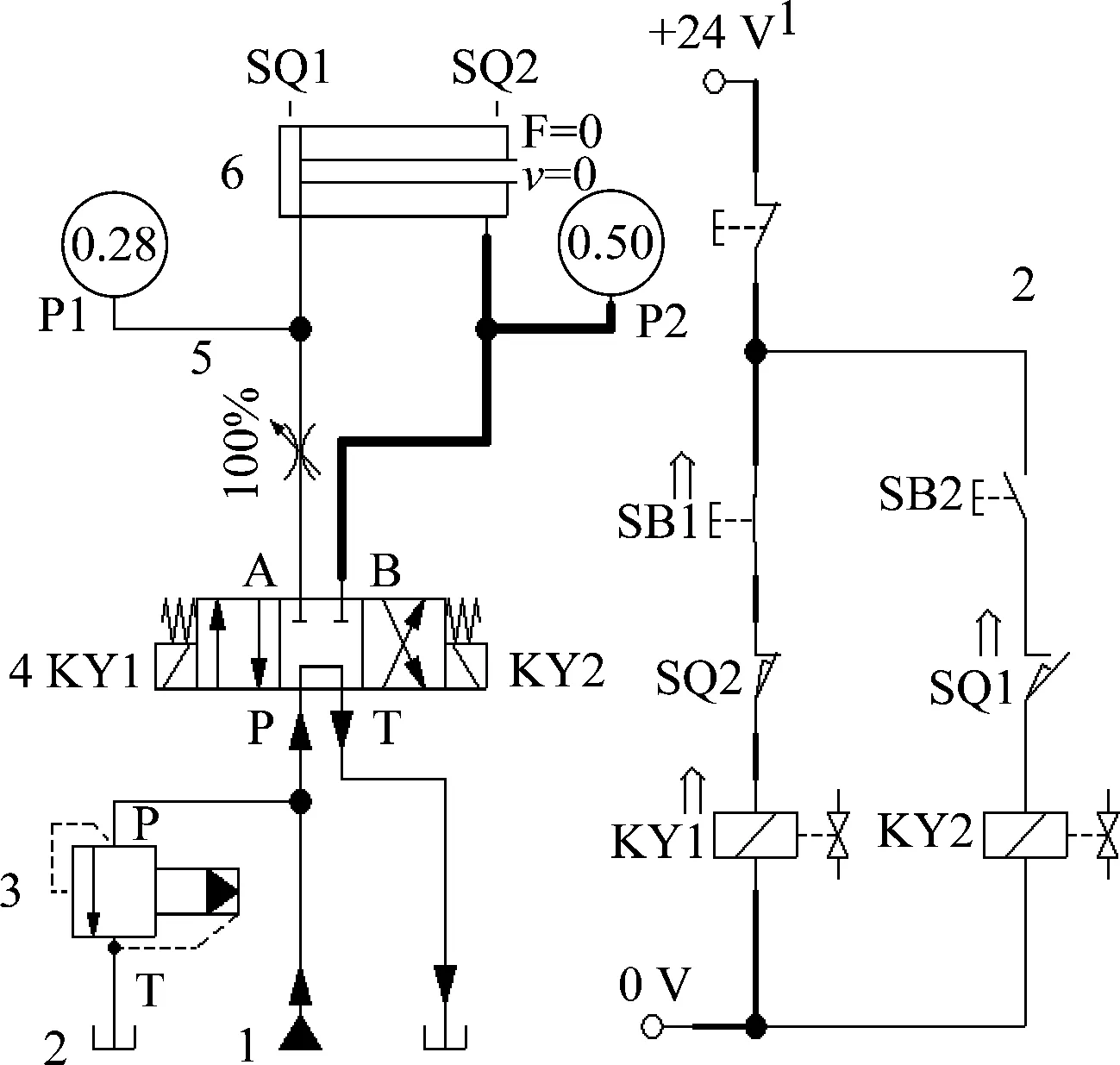
图3 液压滑台的系统仿真

由图3可知,当控制按钮SB1接通时,三位四通换向阀的线圈KY1得电后液压缸伸出,进而在FluidSIM构建的仿真系统中得到压力输出的相关参数。通过仿真实验验证了液压滑台模型的可行性,为后续自适应仿真模型的建立提供了基础。

1.3 液压滑台的基本参数

依据图1、图2,给出了液压滑台的基本参数[2],如表1所示。

2 滑台液压系统的数学模型

2.1 滑台液压系统受力分析

由图2可知,本文以非对称液压缸组成滑台液压系统,其核心结构的原理图,如图4所示。

图4 非对称缸核心结构原理图

如图4所示,当处于工作状态,此阀芯向右移位时,液压缸的输出力与负载间存在一定平衡关系,其平衡方程[3]为

(1)

式中,mt为负载总质量,BP为负载粘性阻尼系数,K为弹簧刚度,FL为活塞上外负载力,AP为活塞的有效作用面积,PL为系统的工作压力,xP为位移的变化量。

本文以液压动力滑台的非对称液压系统为研究对象,进行了必要假设及数学模型的建立[4]:

(1) 忽略液非对称液压系统管道中的流量与压力损失;

(2) 系统所承载的负载总质量不变;

(3) 液压系统的粘性阻尼系数忽略不计;

(4) 液压系统的油路管道对称,且恒压。

2.2 系统压力与位移变化量

根据式(1)可知,当活塞的有效作用面积、活塞上外负载力、弹簧刚度不变时,液压系统的工作压力与活塞的位移变化之间成一定比例关系。结合本文2.1中所述的仿真模型,将式(1)简化为

AppL=Kxp+FL

(2)

式中,K为比例系数,FL为活塞上的外负载力,AP为活塞的有效作用面积,PL为系统的工作压力,xP为位移的变化量。

其作用于系统活塞上的外负载力若恒定,且活塞的有效作用面积不发生变化时。则液压系统工作压力差(PL)与位移变化量位(xp)之间的比例关系为

PL=kxP

(3)

式中,k为比例系数

根据式(3),列举在不同系统工作压力下所对应的活塞位移变化量,如表2所示。

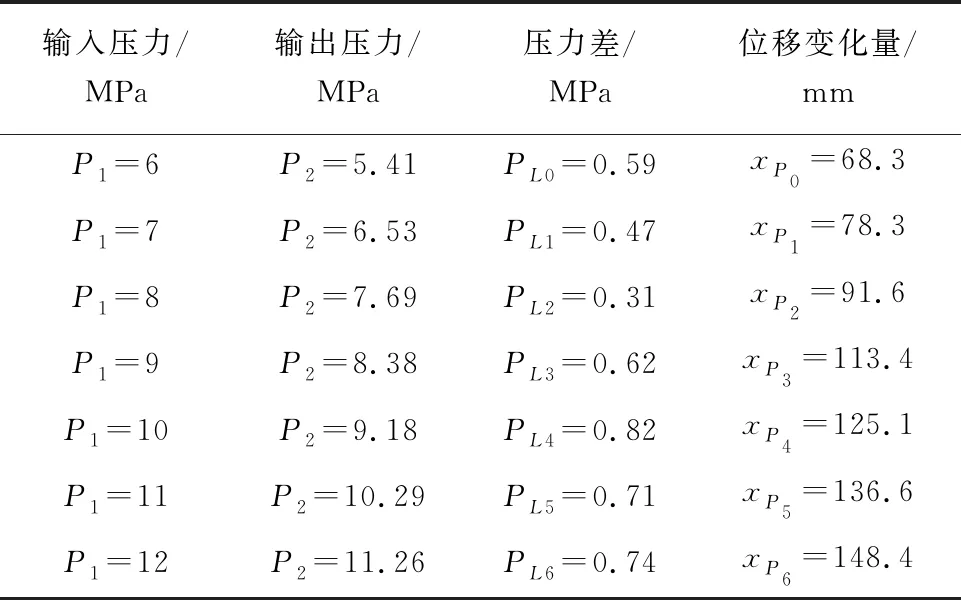
表2 系统工作压力与位移变化量

本文结合表1的数据,以式(3)为基础,构建以比例系数(k)为变量的数学模型,并结合MATLAB软件进行分析[5-7],得到了系统的比例系数。

(4)

根据式(4)可得k≈11.71

3 控制系统的设计

本文结合PID算法中的比例环节,选用Micro-chip公司较为成熟的DSPIC30F2010数字信号处理芯片[8-9]为控制核心。通过PID控制器的比例控制环节不断对参数进行调整,从而实现对比例换向阀的有效控制,进而保证系统压力有效输出。

图5为控制系统的主要工作过程。首先位移传感器完成检测,输出位移变化增量(XP),其次比例反馈环节,按照系统设定好的比例系数(k),向电磁比例换向阀输入适当强度的控制电流,改变其开口大小,完成系统压力、流量、位移的控制,进而达到消除偏差,提高系统的稳定性,实现自适应调节的目的。

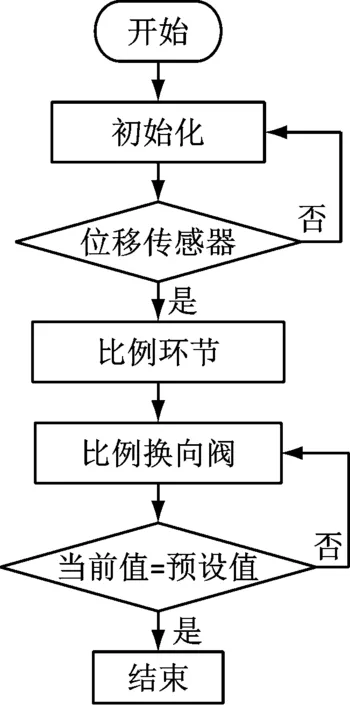
图5 控制系统流程

4 系统仿真与分析

本文利用AMESim仿真软件[10],在进行系统草图的绘制的基础上建立系统仿真模型,同时完成核心参数的设置,并进行仿真运行。分别建立一般与自适应控制系统相应的仿真模型,并对两种模型进行仿真实验,得到各自的工作特性曲线。

4.1 系统模型的建立

打开AMESim软件的电子器件、机械库,完成2种系统的草图绘制,并为对应的元件赋予子模型[11]。由于本设计所用元件均来自AMESim软件标准库,可直接进行参数设置,既赋予对应的值[12],最后通过运行查看相应结果,得到其动态曲线。

4.1.1 一般控制系统的仿真模型

(1) 建立仿真模型,如图6所示。

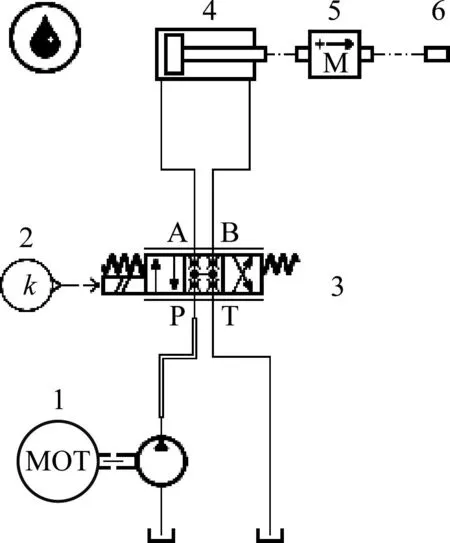
图6 一般控制系统的仿真模型

图6中,1为液压马达,2为控制信号,3为比例换向阀,4为液压缸,5为质量块,6为自由端。

(2) 设定子模型参数,如表3所示。

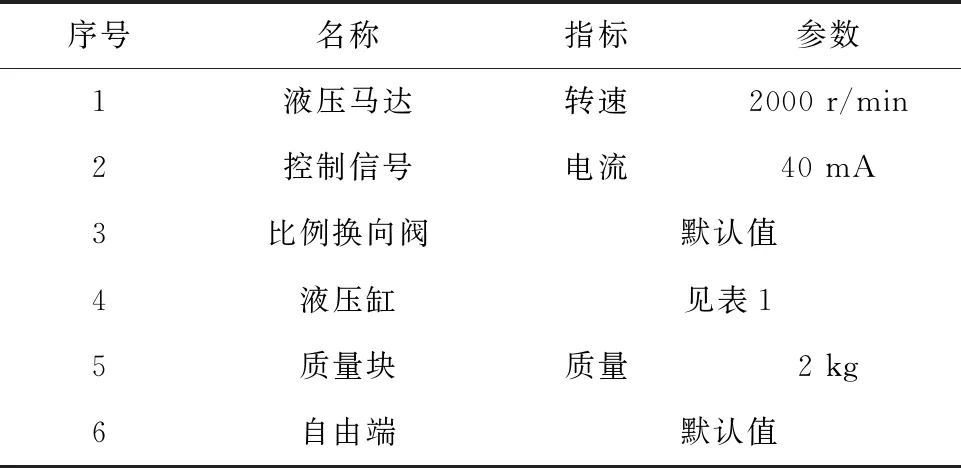
表3 一般控制系统的子模型参数

4.1.2 自适应控制系统的仿真模型

(1) 建立仿真模型,如图7所示。

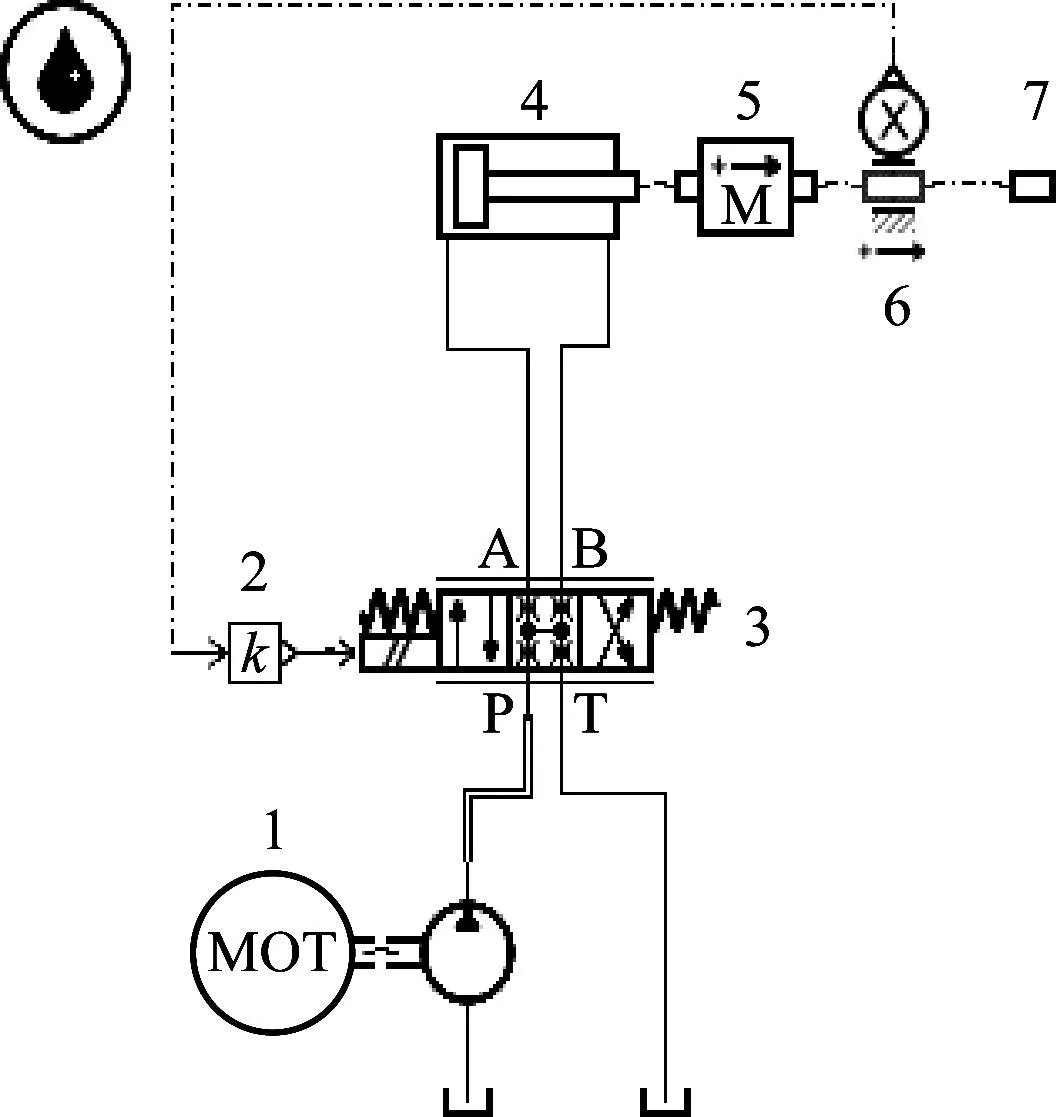
图7 自适应控制系统的仿真模型

图7中,1为液压马达, 2为比例反馈, 3为比例换向阀, 4为液压缸, 5为质量块, 6为位移传感器, 7为自由端。

(2) 设定子模型参数,如表4所示。

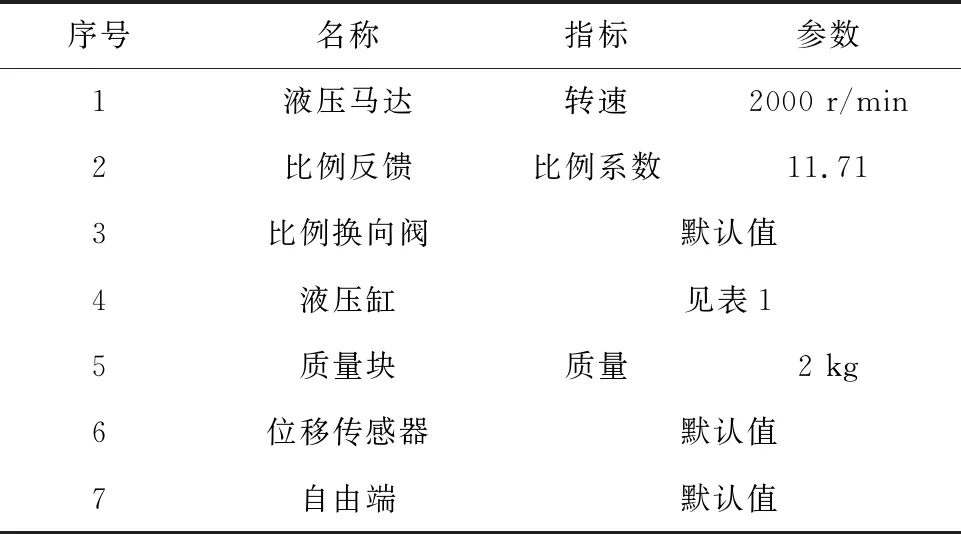
表4 自适应控制系统的子模型参数

4.2 系统仿真与分析

本文在4.1建立的仿真系统的基础上,对一般控制系统与自适应控制系统进行仿真实验。

4.2.1 控制系统的压力变化

依据图6、图7,本文对照表2、表3中的参数,对建立的仿真模型赋值并仿真,得到2种不同控制系统的压力变化特性曲线,如图8所示。

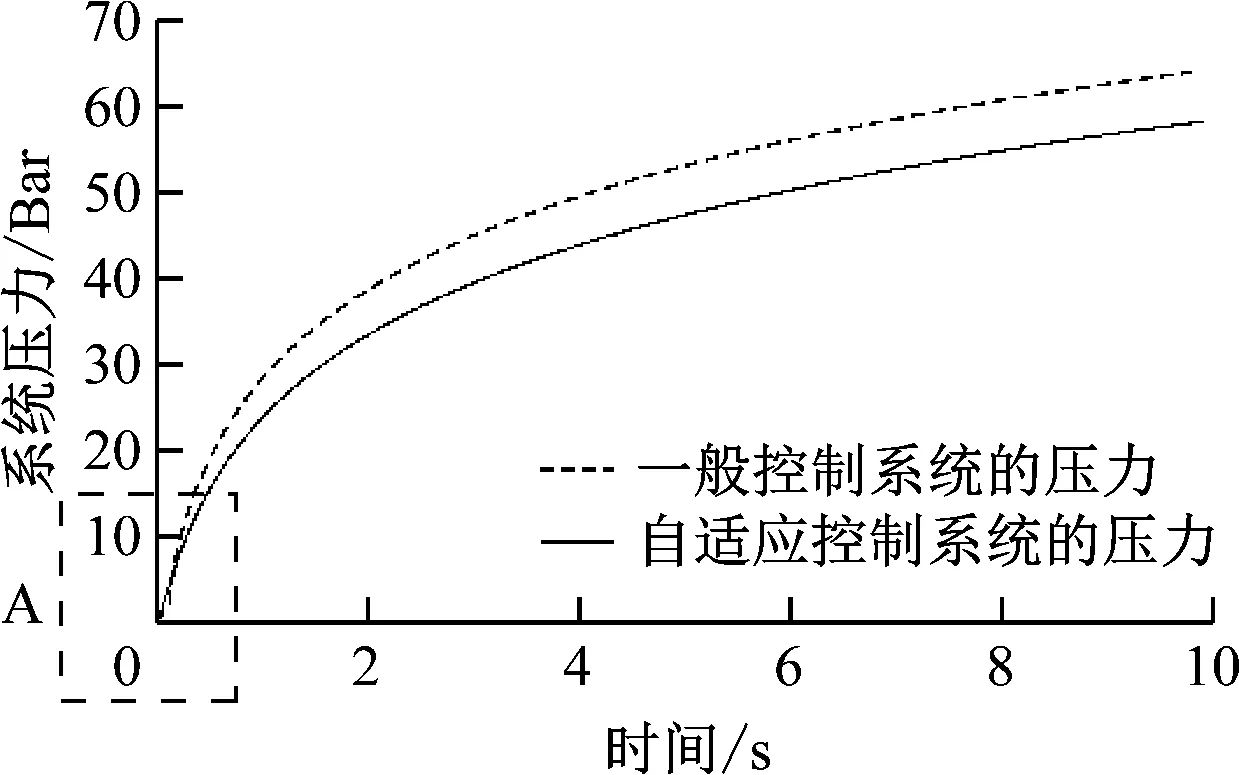
图8 压力变化特性曲线

将图7中的A处进行放大处理,如图9所示。

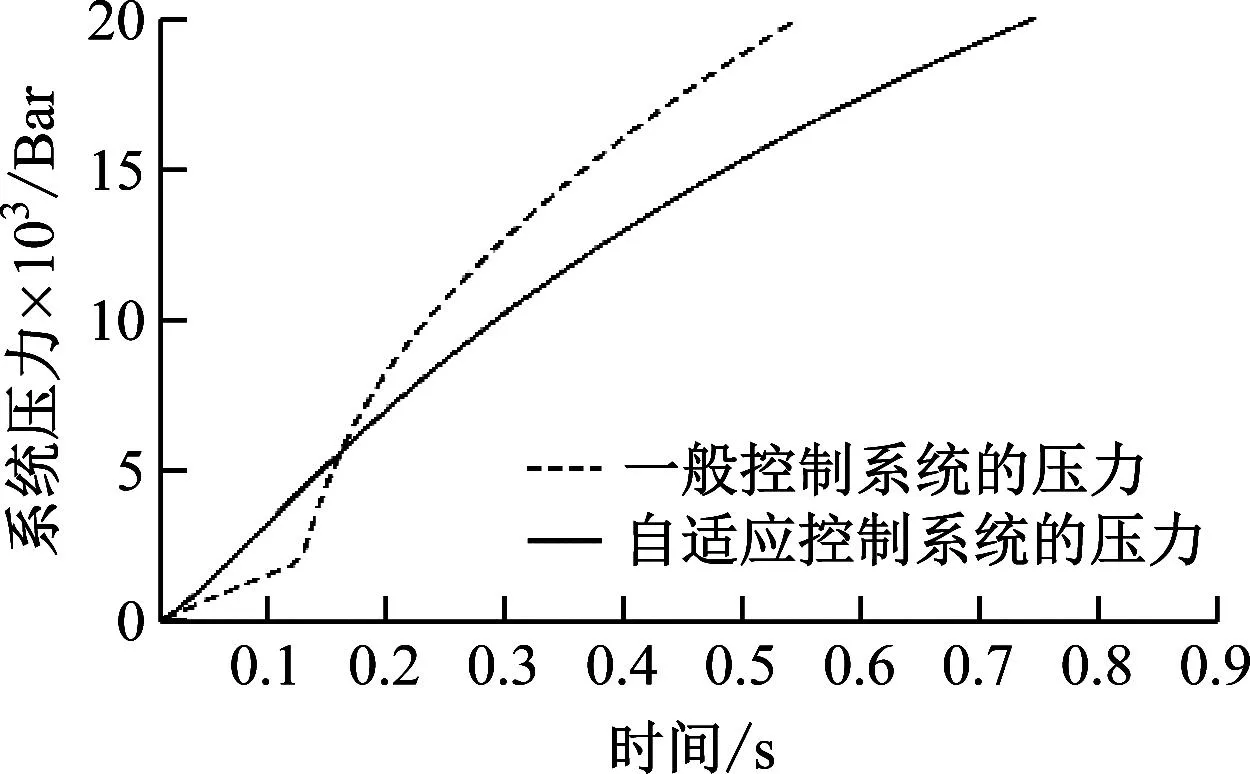
图9 图7-A处的局部放大

由图9可知,在系统工作的开始阶段,自适应控制系统的响应速度高于一般控制系统,同时自适应控制系统的压力变化特性曲线更加平滑,稳定性优于一般控制系统。

4.2.2 控制系统的流量变化

依据图6、图7,参照表2、表3中的核心参数进行仿真,得到2种不同控制系统的流量变化特性曲线,如图10所示。

图10 流量变化特性曲线

由图10可知,在自适应系统的控制下,系统流量震荡明显减少,同时自适应控制系统的流量变化特性曲线更加平滑,稳定性优于一般控制系统。

4.2.3 控制系统负载的位置变化

依据图7,对照表3中的参数进行设置与仿真,得到了在自适应系统的控制下外部负载(质量块)的位移变化特性曲线,如图11所示。

图11 位移变化特性曲线

由图11可知,在自适应系统的控制下,外部负载(质量块)的位移变化先达到稳定状态,稳定性优于一般控制系统。

由图9～图11可知,通过对一般控制系统与自适应控制系统的压力、流量、位置的变化特性分析。证明在相同时间与外部负载的作用下,自适应系统对滑台的控制使其运行更加稳定,进而为滑台的精确控制提供了基础。

5 总结

本文以提高液压滑台的控制精度为目标,分析了滑台液压系统的动态特性问题,并以液压动力滑台的液压执行系统为研究对象,将基于比例控制环节的自适应控制系统应用于液压动力滑台,结果表明:

(1) 在自适应控制系统的控制下,系统压力达到稳态的时间比一般控制系统缩短了0.2 s;

(2) 在自适应控制系统的控制下,系统流量震荡明显减少,系统的响应性得到了很好的优化。

下一阶段,本研究将进在工程应用中进一步研究并验证自适应控制系统在大流量、大输出力液压滑台系统中的合理性以及控制精度等问题。