基于改进蚁群算法的企业供应链网络优化方法

欧静敏

(广东南方职业学院, 信息学院, 广东, 江门 529040)

0 引言

优秀的供应链既能增加企业的经济效益,也能增加顾客满意度,是企业运行与发展过程中要特别关注的“增值链”[1-2]。当前,企业供应链网络优化是提高企业市场竞争力的关键[2-4]。

针对供应链网络优化问题,文献[5]分析了企业集成化供应模式,构建一个集成本、资质、环保和顾客满意度为一体的供应链网络评价指标体系;文献[6]基于Agent模型和Web框架设计了集群式供应链网络模型,为供应链网络优化的实践奠定了基础。针对供应链网络优化问题,多种智能方法被采用,包括神经网络[7]、支持向量机[8]、遗传算法[9]、蜂群算法[10]等,均在不同应用背景下取得了一定的优化效果。

本文提出一种优化供应链网络方法,基于总成本和顾客满意度构建优化供应链网络的多目标模型,并给出了约束条件;采用蚁群算法求解多目标模型,并利用局部搜索改进传统蚁群算法,得出供应链网络的优化方案。利用实际算例验证了模型的求解性能。

1 供应链优化模型

1.1 模型假设

企业原材料由不同地区的多家供应商供应,产品销往不同地区的顾客。供应链网络中包括原材料物流、组织生产、产品分销等,具体结构如图1所示。

图1 供应链结构示意图

对供应链进行模型假设,已知条件如下:①原材料供应商的损耗费用和最大产能;②原材料供应商和分销商的地理位置;③顾客订购产品的数量和对产品的满意度;④原材料和产品的运输方式和运输费用;⑤原材料供应商和产品分销商的污染指数。

1.2 目标函数

(1) 供应链总成本

供应链总成本可以表示为

(1)

式(1)中,i表示生产厂家,i=1,2,…,I,j表示分销商,j=1,2,…,J,l表示产品种类,l=1,2,…,L,k表示顾客,k=1,2,…,K,t表示运输方式,t=1,2,…,T,Xi表示原材料生产厂家的产量,Ci0表示生产厂家i的生产成本,Yj表示分销商j的分销量,Cj表示分销商j的分销成本,Xij表示生产厂家i运送到分销商j的产品量,S1ij表示生产厂家i运送到分销商j的单位运输成本,Qjlkt表示分销商j以运输方式t给顾客k的商品l的数量,S2jlkt表示分销商j以运输方式t给顾客k的商品l的单位运输成本。

(2) 顾客满意度

顾客满意度主要包括顾客购买的产品数量和质量

(2)

(3)

(4)

式(2)～式(4)中,θk表示顾客对于企业生存和发展的重要性权值,γk1表示产品数量对顾客k是否满意的影响权值,β表示顾客k对产品供应量的满意度,γk2表示产品质量对顾客k是否满意的影响权值,α表示顾客k对产品供应速度的满意度,Hjl表示生产商j生产的产品质量,Qjlkt表示分销商j用运输方式t给顾客k提供的商品数量,Fk1表示顾客k对于产品l的质量需求,Ek1表示顾客对产品的总需求量,Ek1表示分销商提供给顾客k的产品总量。

综合供应链总成本和顾客满意度,目标优化函数为

F=minC1+maxC2

(5)

1.3 约束条件

(1) 供应链中生产厂家i的生产量不能超过该厂家的产量上限

Xi≤Ai,max

(6)

式(6)中,Ai,max表示生产厂家i的产量上限。

(2) 分销商j的最大销售量不能超过该分销商的销售量上限

Yj≤Bj,max

(7)

式(7)中,Bj,max表示分销商j的销售量上限。

(3) 从分销商j以各种运输方式销售给顾客的商品l不能超过分销商j的最大销售量。

(4) 所有分销商以各种运输方式销售给顾客k的产品不能超过该顾客的最大需求量。

(5) 分销商j向顾客k用运输方式t销售的产品l不能超过该运输方式的运量上限。

2 基于改进蚁群的模型求解

2.1 编码规则

基于蚁群算法对信息素和启发因子公式,求解蚁群信息素和启发因子数值。局部信息素为

(8)

全局信息素为

(9)

式(8)、式(9)中,ρ1表示蚁群算法中局部信息素的蒸发率,ρ1∈(0,1],ρ2表示蚁群算法中全局信息素的蒸发率,ρ2∈(0,1],τ0表示信息素的挥发量。在供应链目标函数优化过程中,假设τ0=1/dij,dij表示供应链中某条路径的总成本,B表示供应链中某条路径的顾客满意度。

蚁群算法启发因子为

(10)

式(10)中,Ek表示满足供应链目标优化约束条件的可选路径的活动集合,nj表示某路径的后续总成本,λ表示后续成本的权值。

利用概率公式可以计算出对应的概率值,概率值计算方式为

(11)

式(11)表明路径的选择会随着蚂蚁动态变化,并且选择概率与蚁群信息素和启发因子乘积呈现正比关系,其中α和β表示2个可调参数,用来调节信息素与启发因子在路径选择过程中的权重值。得出选择概率后,可以利用轮盘赌方法得出活动列表。

2.2 Pareto档案集和更新机制

蚁群寻优算法初始化后,Pareto档案集设置为空,第一代蚁群检索出的所有解保存在Pareto档案集作为蚁群算法的初始解集合。后续每一代蚂蚁种群检索出的解均与Pareto档案集中所有解进行对比,依据对比结果进行更新。具体更新过程如表1所示。

表1 Pareto档案集更新过程

2.3 局部搜索

基于Pareto档案集和更新机制能够获得蚁群算法的最优解,但最优解的局部最优性能不佳,采用插入邻域和置换邻域对蚁群寻优算法进行进一步的优化。

插入邻域表示利用插入(Insert)操作得到的所有邻域而生成的集合。对于一个包含n个节点的路径,经过Insert操作后,插入邻域的规模可以表示为(n-1)2。令Insert(π,m1,m2)表示插入操作过程:如果m1>m2,则将生成活动列表m1位置上的路径节点插入到m2位置之前;反之,则插入到m2位置之后。经过上述插入操作后,活动列表邻域结构可以表示为

(12)

置换邻域(Swap)就是对活动列表的两个活动位置进行随机交换。已知各个路径节点的邻域解有n(n-1)/2个,令Swap(π,m1,m2)表示置换操作过程。经过置换操作后,活动列表邻域结构可以表示为

(13)

3 算例结果与分析

本节进行算例分析,实验硬件环境为Inter Core i7-10510U,主频1.8 Hz,内存12 GB,显卡为英伟达3070,实验软件环境为Windows 7 64位操作系统,编程语言为MATLAB。

3.1 算例模型

算例是一个由11个制造中心(生产厂家)、9个分销商、6个零售商(顾客)和两型产品构成的供应链网络,其中,1至3号分销商主要负责分销产品1,4至9号分销商主要负责分销产品2。各制造中心的生产参数如表2所示。企业商品的主要零售商分布在周边4个省份,产品的运输方式包括公路(t=1)和铁路(t=2)。各零售商的产品需求质量和数量如表3所示。

表2 产品制造与分销相关参数

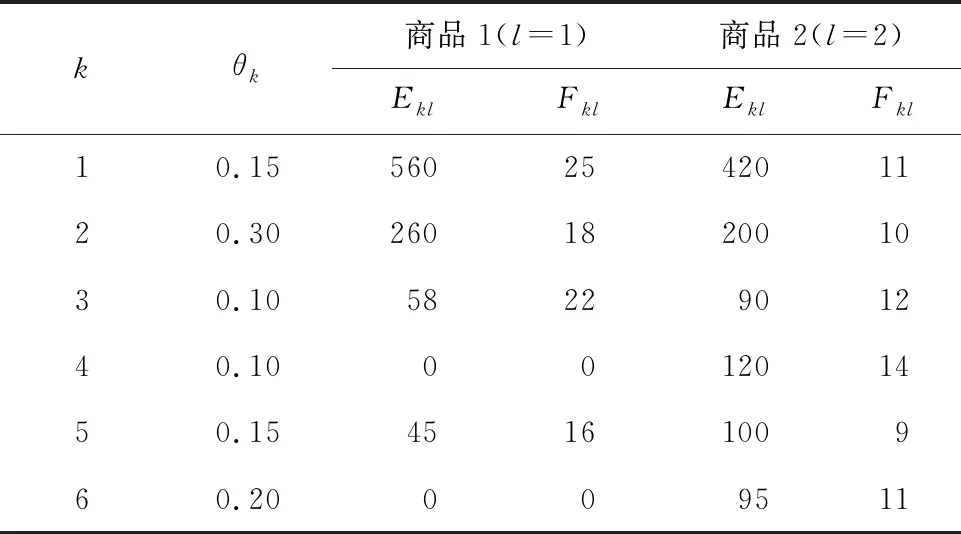
表3 零售商对产品的数量和质量需求

3.2 算例结果

零售商对于商品的数量和质量的权值分别设置为γk1=0.44和γk2=0.56,目标函数中生产成本权重设置为ω1=0.60,零售商满意度在目标函数中的权重设置为ω2=0.40。图2为改进蚁群算法和传统蚁群算法的收敛图。结果表明,传统蚁群算法需要迭代60次达到收敛,而本文改进蚁群算法只需要大约25次,这说明改进蚁群算法具有更快的收敛速度。

图2 收敛速度对比结果

为了验证本文提出的供应链网络优化方法的有效性,考虑到不同指标的评价方向不同,选取一些多目标优化过程中应用非常广泛的指标对算法非劣解集的质量进行测试,具体评价指标为修正距离(MID)、分散性指标(SNS)和多样性指标(DM)[11]。

图3是本文改进蚁群算法获得的多目标供应链优化模型结果。结果表明,供应链网络优化模型的非劣解集呈现出正向线性相关,即供应链网络总成本会随着零售商满意度的增加而增加,这与供应链网络的客观实际是相符的,证明了模型的有效性。

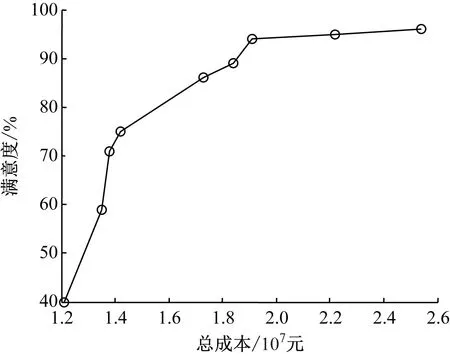
图3 模型运行结果图

企业决策者要在供应链网络优化过程中面临着供应链总成本和零售商满意度之间的矛盾问题,要提高零售商满意度,随之而来的就是供应链总成本上升,但当总成本增加到一定值后,继续增加成本,零售商满意度的增加趋于缓慢,运行本文模型得出的非劣解集能够为企业决策者提供参考方案。

为了验证模型运行获得非劣解性能,统计计算5次运行结果的修正距离、分散性指标和多样性指标值,结果如表4所示。表4结果表明,解S1在解集多样性方面表现更佳,但是在均匀性和修正距离方面不如解S4和解S5。

表4 非劣解评价指标统计结果

为了进一步验证模型对供应链网络优化的求解性能,统计非劣解集修正距离、分散性指标和多样性指标的相对百分比偏差。随机运行模型20次,统计3种评价指标的相对百分比偏差,结果如表5所示,表中还给出了文献[11]提出蜂群算法供应链优化结果。表5统计结果表明,本文模型3种评价指标的相对百分比偏差均低于0.5,优于文献[11]提出的蜂群供应链网络优化方法,证明了本文改进蚁群算法的多目标模型能够有效解决供应链网络优化问题,且精度较高。

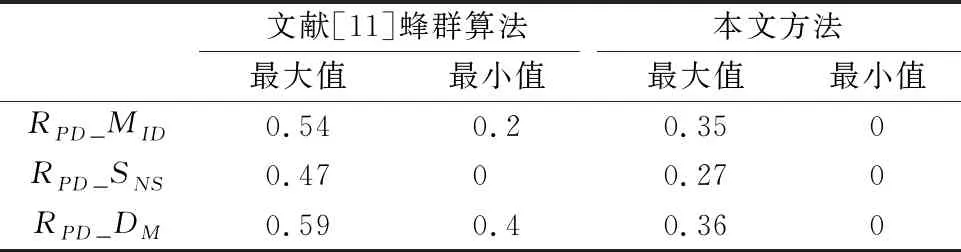
表5 3种指标的相对百分比偏差统计结果

4 总结

本文研究企业供应链网络优化问题,构建一个基于多目标的供应链优化模型,并利用改进蚁群算法求解模型。该模型充分考虑了顾客满意度和供应链总成本,利用局部搜索改进的蚁群算法能够高效地求解模型非劣解集,算例实验验证了模型的有效性。研究内容为企业供应链网络优化提供了一种新方法。