“数形结合”
--测量及不确定度教学模式的改革与研究
史韡朝,徐 崇,孙家军
(辽宁科技大学 理学院,辽宁 鞍山 114051)
物理实验测量中,学生对不确定度概念的理解非常重要,因为它是设计和进行实验以及随后对发现进行解释的基础。不确定度表示的是一个范围,它是不可避免的,即使对科学家来说也是如此。不确定度越小,结果越接近被测量的真值,质量和水平越高,其使用价值也越高;不确定度越大,测量结果的质量和水平越低,其使用价值也越低。在报告物理量的测量结果时,必须给出相应的不确定度,这样便于使用的人评价其可靠性,同时也增强了测量结果之间的可比性[1-4]。因此,测量不确定度是衡量数据质量的一种指标。
教师必须告诉学生,所有测量结果都存在一定程度的不确定性,并且不确定是可以接受的。在实验室中,学生通常会得到计算不确定度的数学公式说明,并期望通过遵循实验室手册提供的说明来理解这些思想。然而先前的研究表明,世界各地的学生在理解测量和相关不确定性方面都有类似的困难。一些学生认为没有必要重复测量,还有一些学生认为可以通过进行更多的测量来确定这种“真实值”。作为最终结果,他们通常只报告算术平均值,在比较数据集时只考虑平均值,很少考虑测量的不确定度[5-6]。因此实验教学的设计不仅应该教授那些用于量化不确定度的数学计算公式,而且应该明确地发展对不确定度的概念理解[7-8]。
与仅用数字表示数据相比,数据的图形化展示可能会减少学生数据分析时的认知负荷,从而为处理测量数据留下更多的认知资源。认知负荷理论认为,只有当信息的提供方式不会使心智能力“超载”时,学习才能有效地进行[9]。例如,如果要求学生比较两个数据集,图形表示方法将有助于评价数据区间是否重叠。虽然数据图形化似乎是比较数据值以及不确定性区间的有效方法,但这一主题国内尚未进行系统研究。本文的研究问题如下:数据的图形化展示是否有助于学生理解测量的不确定度?
1 教学实验
本研究准备了两个版本的不确定性教学方式:即有无测量数据的图形化展示。在大学物理实验绪论课结束后,对学生进行问卷测试,研究数据的图形化展示是否能够提高学生对不确定性的理解。
1.1 研究样本与测量工具
这项研究的参与者由辽宁科技大学化工专业21级两个班级共68名学生组成(每个班各34人),一班为无图形化展示班级,二班为图形化展示班级。
物理测量问卷(Physical Measurement Questionnaire,PMQ)是一项用于衡量学生对测量不确定性理解水平的问卷。它是由开普敦大学的Saalih Allie教授等人开发的。该调查问卷的背景是一项物理实验,它包含8个问题涉及测量过程中的不同步骤(例如“数据收集”或“数据分析”)。每个问题又分为两部分,即:在回答了选择题后,学生们会被要求给出自己的解释证明他们的选择是正确的。
1.2 实验过程
本研究准备了两个版本的绪论课教学方式:在一班课堂上,实验教师讲解数据的误差来源、数据的基本特征(平均值、标准差等)以及如何通过公式来计算A类、B类及合成不确定度;在二班课堂上,除了与一班相同的授课内容外,还提供了原始测量数据在数轴上的辅助图形展示。示例如下:从1米的高度释放没有初速度的球,测量其留在沙子中的直径d(见图1)。问以下三种测量结果,A组和B组的测量结果是否一致?测量结果一:A组为18、25、20、28、24,平均值23;B组为20、28、22、24、31,平均值25。测量结果二:A组为19、22、20、25、24,平均值22;B组为29、32、28、26、30,平均值29。测量结果三:A组为26、30、22、27、20,平均值25;B组为23、11、41、16、34,平均值25。
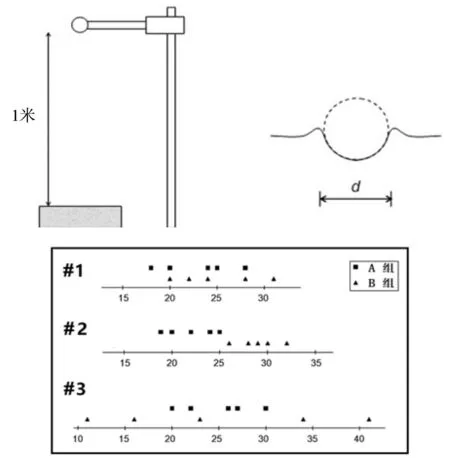
图1 教学示例
2 结果与讨论
2.1 数据的处理
该问卷,学生通常需要15分钟才能完成测试。要求每个问题都写在一页纸上,并要求按照小册子上的顺序回答问题。测试由两位作者独立打分。针对每个问题,学生如果给出正确的答案和正确的解释,将获得2分。如果学生选择了正确的答案并给出了自己不完整的解释,他们就会得到1分。如果给出的正确答案和错误的解释,则学生得0分。最高分是16分。对于分歧,两位评分者进行了协商,统一了认识。为了确定数据的图形化展示是否对学生的分数有影响,进行了方差分析。
2.2 数据分析结果
数据图形化展示的二班学生比没有图形化展示的一班学生平均得分更高(见图2)。
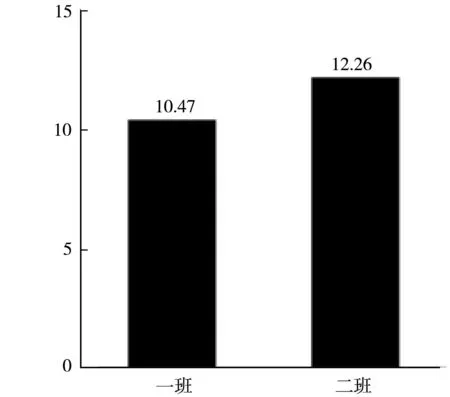
图2 两个班级的平均分数
Shapiro-Wilk检验显示,两个班级的成绩分布为均正态分布(一班W值0.947,p值0.103;二班W值0.940,p值0.062)。Levene’s方差齐性检验p值0.820,大于0.05。数据满足方差所需的假设,因此对两个班级的平均分数进行了方差分析。结果显示,数据有无图形化展示在统计上有显著效应,p<0.01(见表1)。

表1 两个班级平均分数的方差分析
这一结果可能的解释是,数据的图形化表示,可以帮助学生花更少的时间处理数据。这一发现与认知负荷理论相一致,以图形形式呈现数据减少了学生认知负荷,增加了用于处理数据的认知资源量[10]。建议在物理实验课程中加强测量数据的图形化展示。
3 结 论
之前的国外研究表明,数据的图形化展示有助于学生理解数据和测得的不确定度,但这一问题尚未在中国得到系统研究。本次研究,调查了图形表示在理解和解释数据中的作用。结果表明,数据的图形化表示可以帮助学生更好地理解数据和测量的不确定度。

