基于LS-DYNA的深沟球轴承结构参数影响动态性能的研究
倪强,张茜,胡卫平,张雅娜,董玉雪
(瓦房店轴承集团有限责任公司,辽宁 瓦房店 116300)
0 引言
随着现代计算机计算能力的飞速发展,仿真分析已经成为解决复杂工程问题的一种有效手段,有限元仿真方法渐渐被学者们运用到轴承的动力学分析领域。轴承在机械领域中起到至关重要的作用,它是传递载荷及运动关系的重要部件。针对滚动轴承动力学问题,许多学者利用LS-DYNA 软件对其进行了研究。文献 [1] 研究了轴承的参数工况,通过变化径向载荷和转速,对工况参数轴承的动力学特征进行了对比,选出最优的工况参数。文献 [2] 研究了轴承的接触力,通过理论值与仿真值进行对比,证明了仿真模型的准确性。文献 [3] 研究了在不同转速和载荷条件下,得出了轴承内外圈、滚动体的应力分布,讨论了各部件间接触力的关系。文献 [4] 提出了在轴承动力学计算中,运用刚体简化方法来提高计算效率和精度。文献 [5] 对某轴承内圈损伤进行了动力学仿真计算,通过有损伤与无损伤结构的动力学性能对比,得出了各部件应力分布和加速度、速度的波动程度。文献 [6] 利用 LS-DYNA软件建立二维有限元模型,研究了转子不平衡和轴承故障特征频率的关系,并与试验进行了对比,得出了外圈故障频率被转频调制的结论。文献 [7] 通过建立仿真模型,研究了角接触轴承在启动阶段和稳定运行阶段的动态性能参数的变化规律。所以显示动力学仿真分析为轴承结构的准确计算提供了有效方法[8]。
上述文献中学者们均用 LS-DYNA 软件对轴承的接触力、转子不平衡、动态特性、故障特征频率等进行了显示动力学计算分析,但并未涉及到轴承的结构参数变化对轴承动态性能的影响。鉴于此,本文基于国标测试工况,利用 LSDYNA 软件对深沟球轴承进行显式动力学仿真分析,将仿真速度值与理论计算值进行对比,数值比较接近,验证了该模型的可行性。
1 基本模型
当有外载荷或者重力作用时,滚动体受力位置是变化的,由于阻尼的存在和受控于内外滚道的限制,滚动体和保持架的运动滞后于内圈。
按照轴承旋转的特点,在计算分析的过程中做如下假设:
(1)因为几何模型中倒角对结构的应力分布影响较小,所以简化模型不含倒角;
(2)不考虑油膜的影响;
(3)由于结构模型的塑性变形很小,所以结构均为线性弹性材料。
1.1 几何模型
6309 深沟球轴承基本组成结构有保持架、内圈、滚动体、外圈,几何结构参数如表1 所示,其中几何模型中倒角部分简化处理,如图1所示。

表1 6309 轴承基本结构尺寸参数
1.2 有限元模型
通过有限元建模软件对轴承进行实体模型离散化,离散后模型见图2。有限元模型在建立的时候,使用同规格网格尺寸,使同类型模型节点、网格数均相同,防止网格差异及沙漏导致结果不准确。实体模型均为全积分实体单元,载荷区域建立四边形薄壳单元便于加载,同方案对比网格数与节点数相同,网格规模为 33 976 个,节点数为 40 828 个。
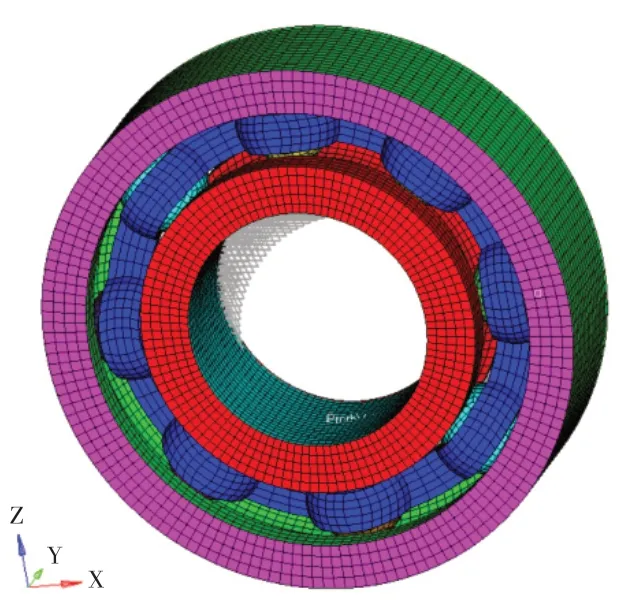
图2 6309 有限元实体模型
1.3 材料参数
6309 轴承的球、内外圈的材料均为 GCr15钢,保持架的材料为冷轧钢板,材料参数如表2所示。

表 2 6309 材料参数
1.4 接触模型
从轴承的接触关系来分有三种接触:球与内、外圈的接触和球与保持架的接触。模型中共建立 24 对接触对,本文中主从面的选择基于凸面为从面、凹面为主面的原则,球一直为从面,其余的部件分别为主面。
本次计算采用A U T O S U R F A C E_T O_SURFACE的接触类型,摩擦系数μc由式(1)
式中:fS为静摩擦系数;fD为动摩擦系数;Dc为指数衰减因数,取值 0.01;Vrel为相对速度。
轴承在运行的过程存在接触摩擦,考虑润滑油和实际摩擦的综合情况[9],摩擦系数如表3 所示。
1.5 约束条件及载荷曲线
(1)约束条件:基于国标测试工况,外圈端部施加 400 N 均布载荷并约束轴向转动(轴向转动约束在关键字中施加),内圈与芯轴接触区域只放开轴向转动,其余全部约束(此约束在关键字中施加),靠近芯轴端面约束轴向位移,施加角速度,测点为外圈上端宽度方向上的中心点[10],如图3 所示。

表 3 静、动摩擦系数
(2)载荷曲线:此次计算共定义三种载荷曲线,分别是重力加速曲线、转速曲线、力曲线。0 时刻内圈为静止转态,0.005 s 时刻内圈转速度提升至最大值,重力及轴向载荷持续施加,如图4 所示。
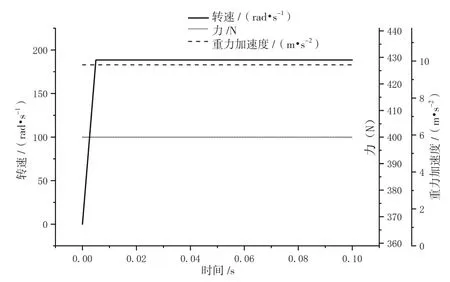
图4 6309 动力学模型载荷曲线
2 速度比较
2.1 仿真模型计算的线速度
轴承内圈是从静止状态在短时间内以一定升速进行加速运动,当达到设定值后做匀速转动。在仿真模型中输出内圈上点 A95738 和保持架上点 B59550 的线速度曲线,其余方案均类似,故只列出一组,如图5 所示。

图5 内圈及保持架速度曲线
在仿真模型内圈及保持架速度曲线中,截取0.02 s 以后的数据并求均值,仿真模型中内圈与保持架的线速度值如表4 所示。

表 4 内圈、保持架的线速度
2.2 理论计算的线速度
保持架转速为:
保持架线速度为:
内圈线速度为:
式中:nm为保持架转速;ni为内圈转速;no为外圈转速;a为接触角;Dw为球直径;Vb为保持架线速度;d为内圈直径。
2.3 线速度理论值与仿真值对比
将仿真模型中内圈、保持架的线速度值分别与理论计算内圈、保持架的线速度进行对比,结果显示仿真值与理论值比较接近,如表5 所示。

表5 线速度理论值与仿真值对比
3 游隙、沟曲率仿真计算结果
3.1 不同游隙对振动加速度的影响
在国标测试工况下,在仿真模型中选取外圈上端宽度中心点为输出点,输出垂向加速度值,计算时间为 0.1 s;当速度稳定后选取数据进行处理,取 0.02~0.1 s 时间内的垂向加速度值数据进行滤波处理和 RMS 计算,滤波方式为带通 50~10 kHz,计算结果如图6 所示。

图6 游隙-加速度趋势曲线
由图6 游隙-加速度趋势曲线可知,在国标测试工况下,随着径向游隙的增大振动加速度整体呈下降趋势。
3.2 不同沟曲率对振动加速度的影响
本文中内圈沟曲率取值范围为0.5 1 0~0.5 2 0、外圈沟曲率取值范围为0.520~0.530,按照间隔 0.001 的方式,内圈沟曲率的取值有 11 种,外圈沟曲率的取值有 11 种,内、外沟曲率排列组合生成 121 种组合方案,计算结果如图7 所示。

图7 内外圈沟曲率排列组合振动加速度等高线图
数据处理方式为选取转速稳定后的数据,取 0.02~0.1 s 时间内的振动加速度数据进行滤波处理和 RMS 计算,滤波方式为带通 50~10 kHz。
在图7 中,横坐标是内圈沟曲率的取值,纵坐标是外圈沟曲率的取值,右边黑白渐变云图是加速幅值,其中黑色区域表明振动加速度值较低,灰色区域代表振动加速度值较高,白色区域代表振动加速度值最高。
图中虚线框里振动加速度值均为较低值,是内、外沟曲率组合的优选参考区域。具体为内圈沟曲率在 0.510~0.512 之间与外圈沟曲率在 0.520~0.523 之间的组合,如图7① 所示。内圈沟曲率在 0.512~0.514 之间与外圈沟曲率在 0.523~0.527 之间的组合,如图7② 所示。内圈沟曲率在 0.510~0.515 之间与外圈沟曲率在 0.527~0.530 之间的组合,如图7③ 所示。内圈沟曲率在 0.515~0.517 之间与外圈沟曲率在0.524~0.526 之间的组合,如图7④ 所示。在这些组合中,振动加速度值均是较低的,故为优选参考区域。
4 结论
(1)游隙仿真结果数据显示,在国标测试工况的约束条件下,随着径向游隙的增大,振动加速度整体呈下降趋势。由于本文根据国标测试工况计算,只施加轴向载荷,所以随着游隙的增大,球与套圈的接触角度也增大,接触刚度就会增大,所以振动值就会呈下降趋势。
(2)沟曲率仿真结果数据显示,在国标测试工况的约束条件下,不同沟曲率排列组合所计算的振动加速度值是有区别的,存在振动加速度较低的优选参考区域,可以在该参考区域内选取合适的沟曲率。
(3)用仿真模型中内圈、保持架的线速度与理论计算的线速度进行对比,数值接近、误差较低,说明用仿真模型来分析轴承动态性能是可行的。

