基于肌球蛋白粗丝力学感知效应的Hill特性式理论研究*

赵晓阳,孙 伟,张俊萍,塔 拉

(1.内蒙古财经大学统计与数学学院,呼和浩特 010070;2.鄂尔多斯职业学院资源工程系,内蒙古 鄂尔多斯 017000;3.内蒙古大学物理科学与技术学院,呼和浩特 010021)

希尔(Hill)于1938年在对青蛙的离体肌肉的研究中发现,在骨骼肌的收缩过程中,施加于肌肉的负荷越大,肌肉收缩的速度越慢,反之亦然,且在肌肉收缩的稳定状态下得到了负荷与收缩速度关系的Hill(希尔)特性式:(T+a)(V+b)=c,其中T和V是肌肉收缩过程中施加于肌肉的负荷与肌肉的收缩速度,a、b和c是常数[1]。

Hill方程式作为肌肉收缩中负荷与速度的经验表达式,在一定负载的条件下能够很好地拟合肌肉收缩中力与速度的关系,一直被认为是骨骼肌收缩的生物物理学基础。随后Huxley提出了肌肉中的肌丝滑行学说,认为Ca2+与细丝上肌钙蛋白的结合使得粗丝上的肌球蛋白与细丝上的肌动蛋白结合,从而引起肌肉的收缩[2]。随后学者们基于肌球蛋白横桥与肌动蛋白丝相互作用的模型,对肌肉收缩中力与速度的关系和肌球蛋白横桥动力学之间的联系进行了深入的研究,得到了Hill方程式的理论表达式[3-5]。然而,这些模型没有涉及肌肉收缩过程中力的平衡的关系,没有考虑肌肉收缩过程中的粗丝的机械力学感知效应。

近年来的实验显示,在骨骼肌和心肌中存在肌肉收缩的双重调节机制,肌肉的收缩不仅受细丝依赖的Ca2+调控机制,还受到粗丝的调控[6]。当粗丝受到的力增大时,从粗丝上伸出的能够与肌动蛋白丝结合的肌球蛋白的数量也增加,从而调节肌肉的收缩特性。粗丝的这种调节机制与收缩期间的力有关,称之为粗丝的机械力学感知效应。

本文依据肌肉收缩机制,考虑肌原纤维结构中力的平衡状态,基于粗丝的机械力学感知效应,建立粗丝调控肌肉收缩模型,推导出肌肉收缩过程中产生的力与收缩速度之间的关系即Hill特性式,并且定量研究了ATP以及Pi的浓度对肌肉收缩中力与速度关系的影响。为更加深入理解肌肉收缩的调控机制提供了新的思路。

1 方法

Piazzesi等[6]在研究骨骼肌的力学特性时发现,当肌丝承受的负荷增大时,结合到肌动蛋白丝上的肌球蛋白的数量增大。文献[7]中的实验数据显示,肌肉收缩过程中,结合到肌动蛋白丝上肌球蛋白的数量m随着负荷T增大而增加,其变化趋势近似线性增长。基于此,本文假设粗丝上被激活的肌球蛋白的数量m随着负荷T线性增大,即

其中m0表示负荷T为零时已处于激活状态的肌球蛋白的数量,α是比例系数。依据肌肉收缩力的平衡条件给出方程

其中F表示肌肉收缩力,f表示弹性阻力,η表示黏滞摩擦系数,V表示肌肉收缩的速度。

在肌肉收缩过程中,部分肌球蛋白与细丝处于结合态(横桥)并产生黏滞摩擦力,若横桥的数量与被激活的肌球蛋白总数m的比例为β,且单个肌球蛋白的黏滞摩擦力为η0V,则总的黏滞摩擦力ηV=βmη0V。 由式(2)可得

将式(1)代入式(3)得

将式(5)代入式(4)得

整理式(6)得

显然,式(7)与Hill方程(T+a)(v+b)=c的形式相同,且

同时,式(7)也与Hill方程的另一种形式(T+a)(v+b)=b(T0+a)完全一致,其中T0=F—f为导致肌肉收缩速度为0的最大负荷(停止力)。

为了比较不同条件下肌肉收缩的Hill特性,通常将(T+a)(v+b)=c做归一化处理,即(T/T0+a/T0)(v+b)=c/T0。为方便计算力与速度的关系并与实验数据比较,将式(6)做归一化处理为

以上依据粗丝的力学感知效应,假设肌肉收缩过程中被激活的肌球蛋白数量与粗丝承受的负荷呈线性关系,由此推导出了肌肉收缩力与速度的Hill关系。以下将通过计算分析,论证本文给出的式(7)的合理性,并对Hill方程中各个参数的含义给出新的解释。

2 结果与讨论

2.1 ATP浓度对Hill特性的影响

肌肉收缩的张力来自肌球蛋白水解ATP 获得的能量,ATP 的浓度对力与速度曲线的特性有显著的影响。文献[8]测试了不同ATP 浓度条件下骨骼肌和平滑肌肌丝的力与速度关系。本文依据式(7)及式(8),计算各种ATP 浓度对应的Hill特性式,与该文献实验结果对比,并讨论各个参数的具体含义。

式(7)中,F表示肌丝收缩产生的力,在肌球蛋白数量足够多的情况下,F的大小与ATP的浓度成正比[8],即F=k F[ATP],k F是比例系数,单位是p N/μmol。f表示弹性阻力,与ATP浓度无关。早期实验中[9-10],肌纤维包含弹性成分titin,弹性阻力f主要由titin产生,力的大小与肌纤维的长度有关。近年来有关力与速度的某些实验剔除了弹性成分titin,仅考察粗丝和细丝之间的作用力,这类实验中,弹性阻力来自肌球蛋白头部被动脱离肌动蛋白丝的拉拽作用[11]。在Hill特性的实验中,肌节长度不断变化,根据文献[12-13],弹性成分titin的拉力可表示为肌节长度l的函数f=18l3—115l2+255l—188。实验测试得到的弹性阻力应当是平均值,在Yasuda等[14]所做的实验中,骨骼肌肌丝长度l变换的范围为2.4～3.2μm,均值为2.8μm,由此可得到f的取值范围介于10～40 p N,均值约为20 p N。T0表示肌肉收缩的速度V为0时对应的最大负荷,在数值上近似满足T0=F—f。

Hill曲线的曲率由a=m0/α决定,其中α为式(1)中新增肌球蛋白数量与负荷T的比例系数,本文假设为α常数,m0表示没有外力作用时处于激活状态的肌球蛋白的数量。依据文献[15],在没有负荷(T=0)的条件下,参与肌肉收缩的肌球蛋白的数量m0随着ATP浓度的增大而增大,在一定的浓度范围内,二者近似为线性关系。基于此,本文假设m0=k m[ATP],其中k m是比例系数。在肌肉收缩的实验中,通常[ATP]的最大值不超过1500～2000μmol[6],而一个肌节中肌球蛋白的数量大约300[7],参与ATP水解循环(被激活)的比例一般不超过2/3[8],即在ATP饱和的条件下,200≤m0≤300,由此可以推算k m的取值区间为[0.1,0.2]。

式(7)中的β表示横桥的数量与被激活的肌球蛋白总数m的比例。β的数值可以由肌球蛋白水解ATP的力学化学循环过程中各类状态的比例计算,最简单的数学模型是二态模型。二态模型将肌球蛋白与肌动蛋白丝的结合过程分为结合态(状态A)和分离态(状态B),如图1所示。肌球蛋白处于结合态时形成横桥,横桥的数量与被激活的肌球蛋白总数m的比例β也就是状态A的所占的比值。

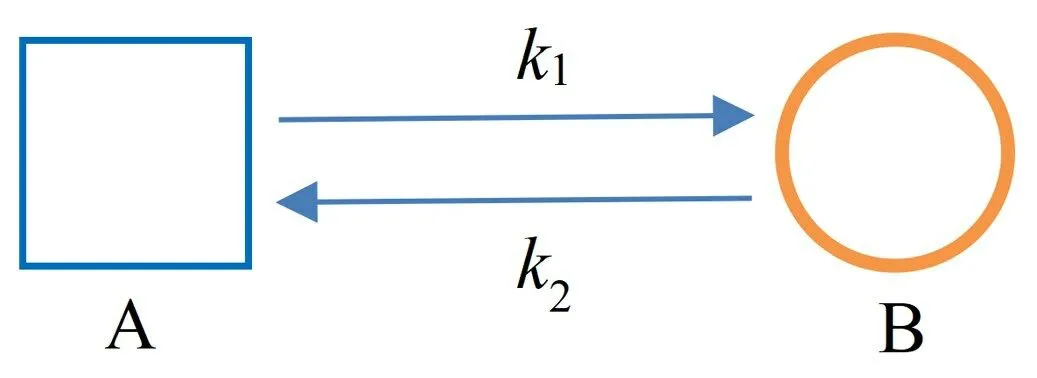
图1 球蛋白二态机械化学循环图Fig.1 Two-stage catalytic cycle of myosins

设状态A→B的反应速率为k1,B→A的反应速率为k2,易知系统的定态解β=k2/(k1+k2)。本文利用二态模型计算肌肉收缩时的黏滞摩擦力,而摩擦力主要来自僵直态,因此图中从状态A到状态B表示处于僵直态的肌球蛋白结合ATP后脱离肌动蛋白丝的过程,其反应速率k1=K T[ATP]。状态B到状态A 包含肌球蛋白再次与肌动蛋白丝结合,以及释放Pi和ADP的过程。由于释放Pi的速率远大于释放ADP的速率,所以图中k2的值主要取决于释放ADP的速率。肌球蛋白释放ADP的速率与其头部承受的拉拽力有关,释放速率通常随着负荷增大而增大[16]。当肌球蛋白所处溶液中ATP的浓度增大时,肌肉收缩力F随之增大,肌球蛋白头部承受的拉拽力也会增大。因此,在本文的仿真计算中,反应速率k2的值在给定的数值范围内随着ATP浓度增大而增大。

基于上述实验数据和推算,列出式(7)中各个参数的取值范围,如表1所示。依据式(8),计算不同ATP浓度条件下力与速度的关系曲线如图2所示。

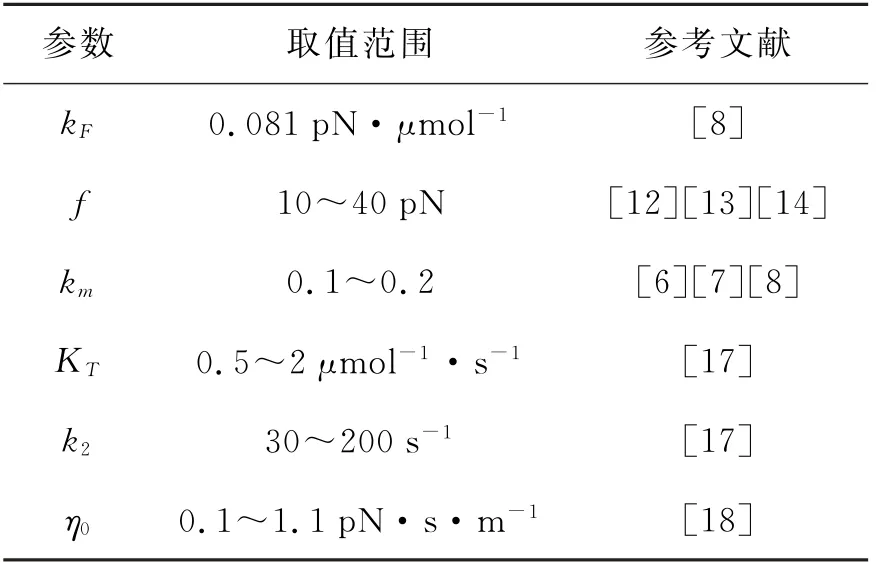
表1 二态模型中的参数选取Table 1 Parameters of two-stage catalytic cycle

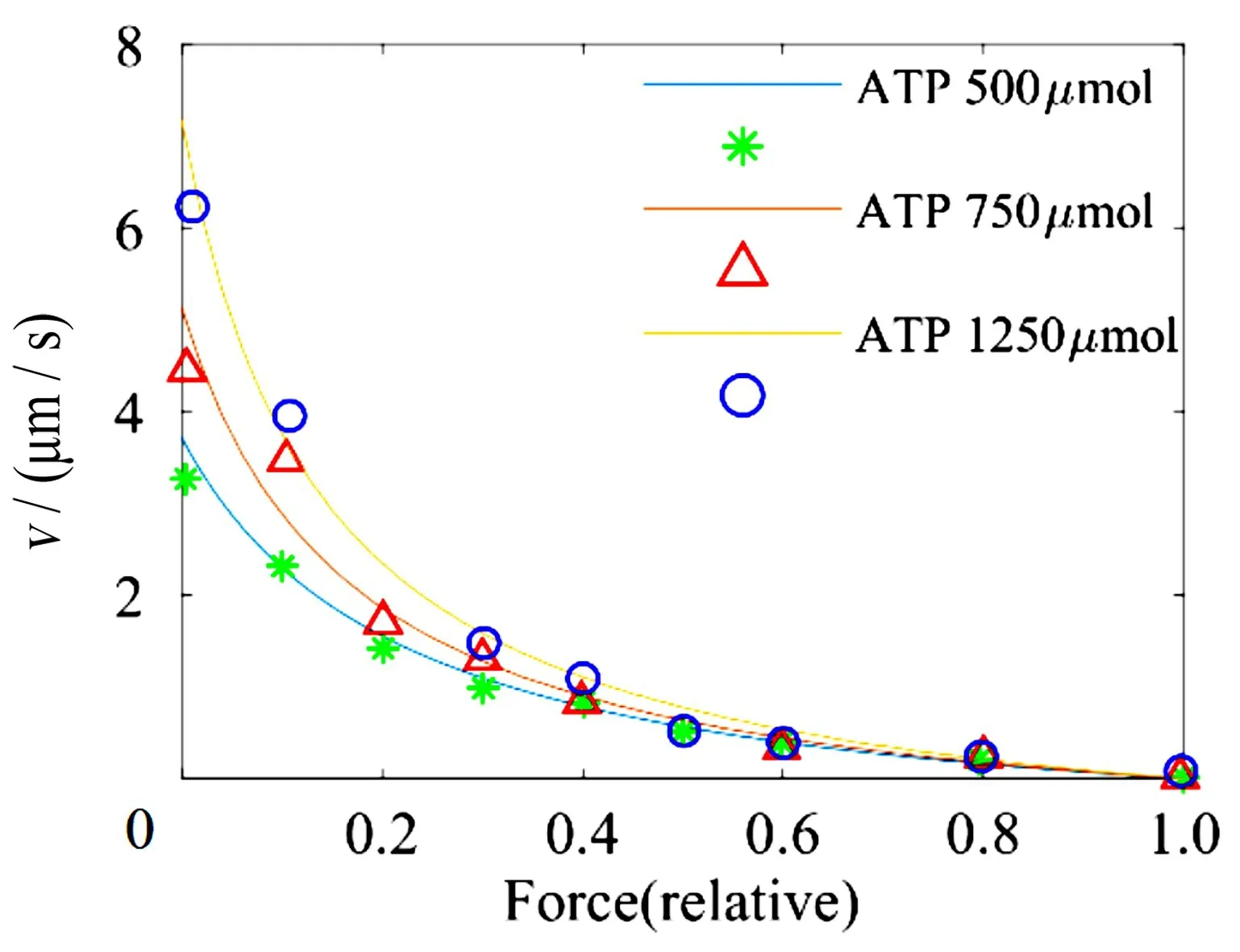
图2 不同ATP 浓度条件下,肌球蛋白微丝中力与速度关系Fig.2 Force-velocity relationship in skeletal myosin filaments with different ATP concentrations

图2中的3条力与速度的曲线,是依据本文建立的模型拟合的理论曲线,3种不同的颜色分别代表了ATP浓度在500μmol、750μmol和1250μmol时的理论曲线。Cheng等首次使用完整的天然肌球蛋白丝,研究了分离的肌球蛋白丝与荧光标记的肌动蛋白丝相互作用产生的力和负载的关系,并且使用了新的技术,使得这一系统中的ATP 的浓度与生理浓度相同。在其实验中,3 种不同生理ATP浓度之下的实验数据分别表示为图中的星号、三角形和圆圈[8]。由图中显示的情况可见,依据本文模型计算的结果与文献[8]的实验数据基本吻合,表明本文提出的粗丝力学感知效应的定量表达式虽然简单,但却具有一定的合理性。

Cheng等[8]统计了大量的实验结果,获得了不同ATP 对应的Hill特性归一化曲线的曲率m0/(αT0)(见文献[8]的表1),通过计算可以得出m0/α的数值近似随[ATP]线性增长,在假设α为常数的前提下,m0的值也与[ATP]线性相关。这一结论与本文给出的m0=k m[ATP]是一致的。

2.2 Pi的浓度对Hill特性的影响

文献[19]研究了多种Pi浓度条件下力与速度的关系,实验研究发现Pi的浓度对于力与速度的关系影响不大。为了考查Pi的浓度对力与速度的关系的影响,考虑肌球蛋白水解ATP 的机械化学循环的四态模型,如图3所示。

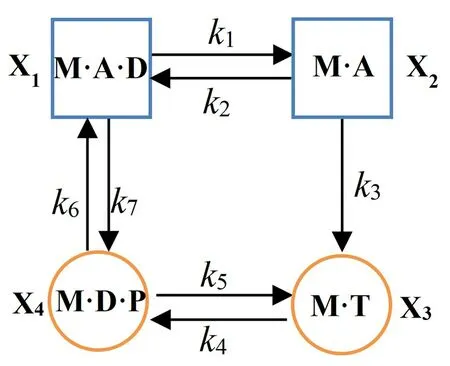
图3 肌球蛋白四态机械化学循环模型Fig.3 Four-stage catalytic cycle of myosins

图中方框表示肌球蛋白与肌动蛋白结合,圆圈表示二者脱离;M 表示肌球蛋白(myosin),A 表示肌动蛋白(actin),T 表示底物ATP,D 表示ADP,P表示水解产物Pi。M·A·D 表示肌球蛋白与ADP 结合且与肌动蛋白丝处于强结合状态;M·A·D 态的肌球蛋白复合体释放ADP后,导致肌球蛋白与肌动蛋白的结合状态成为僵直态M·A;ATP结合到M·A 中的肌球蛋白头部,使得肌球蛋白与肌动蛋白丝分离,同时肌球蛋白与ATP结合,形成M·T;M·T 中的ATP水解为ADP和Pi,形成肌球蛋白与ADP和Pi相结合的状态M·D·P,此时与肌动蛋白依然处于分离状态;M·D·P状态中水解产物Pi的释放,使肌球蛋白与ADP的复合体和肌动蛋白重新结合回到状态M·A·D。X1～X4分别表示的状态,k i表示各状态之间转换的速率常数。设x i表示处于各状态Xi的肌球蛋白的归一化比例,则依据质量定律可得:

且x1+x2+x3+x4=1。

其中参数k6表示M·D·P释放Pi的速率,而k7表示M·D 结合Pi生成M·D·P的速率常数,则在整个水解循环过程中,只有速率k7与Pi的浓度有关,假设k7与[Pi]成正比,即:

由上述讨论可知,肌球蛋白处于结合态时形成横桥,因此横桥的数量与被激活的肌球蛋白总数m的比例β也就是状态X1和X2所占的比值。则

考虑ATP 浓度一定情况下,Pi的浓度对Hill曲线的影响,将式(9)代入到式(7)和式(8)中,选取的参数m0、f、α、η0 同表1,γ取值为0.4,其余参数如表2所示。

表2 四态模型中的参数选取Table 2 Parameters of four-stage catalytic cycle

依据式(8),计算不同Pi浓度条件下力与速度的关系曲线如图4所示。

图4给出了依据本文的四态模型计算得到的不同Pi浓度下的力与速度的曲线,由结果可知,Pi的浓度对力与速度曲线的影响非常小,并且该结果与Månsson 等[19]在2021年的研究结果基本一致,进一步说明了本文建立的肌肉收缩过程考虑粗丝力学感知效应模型存在一定的合理性。

2.3 参数a、b的含义

Hill方程中,参数a、b的含义及其取值仍然没有定论。文献[22]回顾了有关肌肉收缩Hill特性的实验结果,表明在不同的实验条件下,a、b的值是不同的。

由以上讨论可知a=m0/α,表示的是零负荷时激活的肌球蛋白数量与单位负荷下增加的激活肌球蛋白数量之间的比值,反映了负荷对激活肌球蛋白数量影响的强度,而在负荷作用下激活肌球蛋白的数量在一定程度上反映了肌肉的收缩功能的强弱,可见该比值越大,即a值越大,说明负荷对肌肉性能影响越小,该值越小反映负荷对肌肉性能影响越大。而负荷为零时的激活肌球蛋白数量m0与ATP的浓度有关,所以当[ATP]不同时,a的数值也会随之发生变化,与文献[23]的结论是一致的。b=1/(αβη0),表示的是在单位负荷作用下增加的横桥在单位速度时产生的黏滞力的倒数,在该表达式中,β和η0是常数,所以该数值的大小由α确定,也反映了负荷对肌肉性能的影响。

3 结论

骨骼肌和心肌中存在肌肉收缩的双重调节机制,肌肉的收缩不仅受到细丝依赖于Ca2+调节蛋白的结构变化的控制,还受到粗丝的机械力学感知效应的调控。当粗丝受到的力增大时,从粗丝上伸出的能够与肌动蛋白丝结合的肌球蛋白的数量也增加,从而调节肌肉的收缩特性。粗丝的机械力学感知效应反映了力对肌肉收缩的影响,因此粗丝的机械力学感知效应对于理解肌肉收缩的内在机制具有非常重要的作用。描述肌肉中负荷与速度关系的Hill特性式反映了肌肉中负荷与肌肉收缩速度之间的关系,被认为是肌肉生理学的基本原理,对于理解肌肉收缩本身的机制、治疗相关肌肉疾病、理解肌肉效率与肌肉疲劳,以及开发肌肉样性质的机器人技术及假体应用的研究具有重要指导意义。因此在研究肌肉Hill特性时,有必要考虑粗丝的机械力学感知效应对肌肉收缩的影响。

已有文献通过实验证明,粗丝上伸出的肌球蛋白(被激活)的数量随着粗丝承受的负荷增大而增多,但是二者之间的定量关系尚不明确[7]。本文首次提出粗丝力学感知效应模型:肌球蛋白被激活的数量与承受的外力成正比,即式(1)。考虑了粗丝的机械力学感知效应,从肌肉中力的平衡角度出发,推导出不同的ATP浓度条件下骨骼肌肌原纤维力与速度关系的Hill式(T+a)(v+b)=c,所得结果与Hill特性的表达式完全一致,并给出各参数a、b的数学表达式,以新的角度解释Hill方程中各参数的具体含义。进一步考虑ATP浓度和Pi浓度对Hill特性曲线的影响,从本文理论模型中得到的不同ATP浓度和Pi浓度下的Hill特性曲线与近期一些较新研究成果的结论基本一致[8,19]。

近期的研究表明,粗丝上伸出的肌球蛋白的数量当粗丝承受负荷较小时可能与其所承受的外力成正比,但是当其所承受的外力较大时,就会表现出一定的非线性的关系[7]。但是本文没有考虑二者之间的非线性关系,二者的非线性效应可能对肌肉收缩中力和速度的关系产生影响。已有一些研究表明,在较大负荷作用下,Hill特性曲线将会偏离双曲线形式[23],这可能与较大负荷时粗丝的机械力学感知的非线性效应有关,需要在今后的工作中进一步深入研究。