活性粒子的运动属性和堆积密度诱导多种涡旋模式及其转变*
蒋楚楚,郑 宁,刘 伟
(北京理工大学物理学院,北京 100081)
活性物质是一类由自驱动单元组成的非平衡系统,它能将自身储存的能量或从外界环境所吸收的能量转化为定向运动[1]。自然界中蕴涵着丰富多样的活性物质,例如微观尺度上的马达蛋白,它能够利用ATP水解产生的化学能驱动自身沿微管或微丝定向运输货物[2]。在介观尺度上,藻类、精子等会转动鞭毛进行自驱运动[3]。而在宏观尺度上,鱼群[4]、鸟群[5]、羊群[6]、人群等都是活性物质。除了生命活性粒子,越来越多的人造活性粒子随着科技发展已经出现在人们视野中。常见的有Janus胶体颗粒[7]、机器人[8]等。因为自身固有的非平衡特性,大量活性粒子组成的复杂系统会表现出新奇的自组织行为与动力学,例如自发团簇[9]、边界流[10]、相分离[11-12]、湍流[13-14]、涡旋[15]、定向输运[16]等集体现象。
在活性物质自组织集群行为中,涡旋运动就是其中的一类典型。从微观尺度到宏观尺度,从生物系统到人造系统,我们都可观察到涡旋运动,这表明涡旋运动是活性物质中一种普遍现象。Sumino等[17]在动力蛋白驱动的微管中发现了大尺度晶格涡旋的存在。他们发现微管在碰撞时,相互对齐的概率很高。在微管密度高时,这种对齐作用会导致平均长15μm 的微管自组织成直径在400μm 左右的涡旋。在涡旋内部,微管顺时针和逆时针循环流动,且在经历较长的时间后,涡旋就会形成大尺度的晶格结构[17]。在细胞尺度上,研究者们还发现了细菌悬浮液中的细菌涡旋。Liu等[18]研究了流体黏弹性对细菌涡旋的影响,他们将大肠杆菌纯化的基因组DNA 添加到大肠杆菌细胞悬浮液中。当DNA 浓度被稀释时,细菌悬浮液呈无序状态,几十μm 的细胞以瞬态涡流或射流的形式进行小规模集群运动,这称为细菌湍流或中尺度湍流。当DNA 浓度上升到约50 ng·μL—1时,实验观察到整个细菌悬浮液以恒定角速度顺时针或逆时针旋转,形成mm 尺度单向涡旋,这和细菌瞬态微尺度涡旋不同,因此将毫米尺度涡旋称为大尺度涡旋[18]。除了在微介观尺度上发现的涡旋运动,宏观尺度上也存在自组织涡旋运动。Silverberg等[19]研究了重金属音乐会上的人群行为,他们观测了数千段拍摄视频,发现高密度人群的集体行为会出现两种形态:一种是参与者们随机移动,无方向性地随机碰撞,即无序气体状态,称为mosh pit,另一种是自发相位分离,形成涡旋,即有序涡旋态,称为circle pit[19]。
涡旋运动不仅出现在生物活性物质系统中,在人造活性物质系统中也有所体现。Quincke roller是一类常见的人造活性胶体粒子,通过外加直流电场可以使它一边旋转一边定向运动。Bricard等[15]在研究Quincke roller的集群行为时,发现当活性粒子的堆积密度达到一定阈值时,通过施加电场,最终会自组织成一个稳定涡旋[15]。除了在均匀自由环境中活性胶体会形成自发涡旋,研究人员随后发现在受限微流通道中,活性粒子群也会形成有序涡流格相,并且涡格平均拟能会呈现出周期振荡[20]。涡旋不仅可由自推进活性粒子所产生,手性活性物质同样也可以产生涡旋。上海交通大学张何朋团队利用两个反平行排列的Hexbug机器人实现了自转的活性转子,在一定的转子堆积密度条件下,该活性转子会在容器的边界处自发地形成拓扑边缘流,粒子系统角速度沿着容器径向方向振荡衰减,其可被看作是一种特殊类型的涡旋[11]。类似的现象也出现在振动粒子系统[16],我们将带有倾斜腿的颗粒齿轮放在振动平台上,齿轮非对称的腿部结构将竖直振动转化为定向自转,从而形成手性转子,这种手性转子在高密度条件下也涌现出拓扑保护边缘流。
活性物质涡旋运动的研究一般都是围绕活性粒子数目、边界条件以及活性粒子周围介质来开展,而很少专门考虑活性粒子本身运动属性对涡旋的影响。活性粒子根据自身运动状态,可分为线性活性粒子(具有定向平移和随机旋转)[21]、转圈活性粒子(既具有定向平移又具有定向旋转)[22]和活性转子(具有随机平移和定向旋转)[23-24],粒子不同的运动属性很可能会产生不同类型的涡旋行为。此外,该研究也具有现实意义,因为它反映了活性物质在不同环境中可以主动调整个体运动属性来形成不同集体运动状态,从而粒子群体能更好地适应环境变化或根据环境变化实现不同的功能。本文使用Hexbug玩具机器人作为研究对象,通过调整机器人的内部振动马达以及机器人支撑腿的弯曲程度,制作3种不同运动属性的活性粒子。我们在二维容器中,选择不同粒子的堆积密度,实验研究不同运动性质的活性粒子所形成的自组织涡旋运动。通过所记录的视频,我们提取粒子群体的平均流速场并进行比较,半定量刻画了活性粒子从瞬态体涡旋到稳定体涡旋乃至边界流涡旋的转变,为活性粒子的涡旋运动提供了更丰富的内涵,以及为实现集群功能的灵活切换提供了新思路。
1 活性粒子的单体运动性质
玩具机器人,也称为Hexbug玩具虫,是消耗电池能量而实现定向运动的人造活性粒子。玩具机器人近似为长方形结构,长约4.5 cm,宽约1.3 cm,身体两侧各均匀分布5条向后倾斜的弹性橡胶腿,如图1(a)、(b)所示。玩具机器人通过1.5 V 的纽扣电池驱动身体内部的偏心轮马达,马达提供竖直振动并带动机器人的腿也上下振动,通过弹性腿和水平面的碰撞和摩擦,马达提供的竖直动量就转化为了机器人的水平动量,从而实现它在水平面上的自驱定向运动,同时马达振动的噪声也使机器人随机改变运动方向。
为了防止玩具机器人在相互碰撞中倾倒,也为保证机器人之间的相互作用为各向同性,我们为玩具虫设计了圆形外壳。外壳中间是可嵌套玩具虫的长方形槽,槽两侧镂空,如图1(c)所示。该圆壳通过激光切割机切割有机玻璃板而制成,直径为50 mm,高度为15 mm。我们将玩具机器人嵌套在圆形有机玻璃外壳中,通过调整机器人支撑腿的弯曲程度,制成了实验所需的自驱直线粒子、绕圈粒子和准自转粒子。其中为了使绕圈粒子和准自转粒子的旋转半径区别更加明显,我们将玩具机器人的一侧腿适当剪短,使其几乎处于原地自转,制备出了效果显著的准自转粒子。
活性物质的运动方程可以描述其单体运动。考虑单个粒子处于二维均匀空间各向同性的平面上运动的简单情况,即周围环境没有障碍物和其他粒子。在同质环境中,布朗粒子的平移扩散和旋转扩散是独立的,而活性布朗粒子由于具有自驱动速度v,其运动方向会受到粒子旋转扩散系数的影响,导致粒子取向的旋转和粒子平移运动微分方程的耦合。因此活性布朗粒子的运动方程为[25]:其中x,y是粒子的位置坐标,φ是粒子的取向角,ξx、ξy和ξφ分别为不同方向白噪声随机项。D T=k BT/6πηR是平移扩散系数,其中k B是玻尔兹曼常数,T是绝对温度,η是流体黏滞系数。同时粒子还要经历由时间尺度τR来定量的旋转扩散系数,即D R==k BT/8πηR3。对于手性活性布朗粒子,在二维平面上不仅有平动运动方程,而且粒子的取向φ也会以角速度ω旋转。因此二维手性活性布朗粒子的运动方程为其中ω的符号决定活性粒子的手性。
在实验中,我们在玩具机器人的首末两端贴上标签,拍摄单个自驱动直线粒子、绕圈粒子和准自转粒子的运动过程,通过粒子追踪技术得到相应的运动轨迹,即粒子每个时刻的坐标信息。图2给出了以上3类活性粒子典型的运动轨迹。
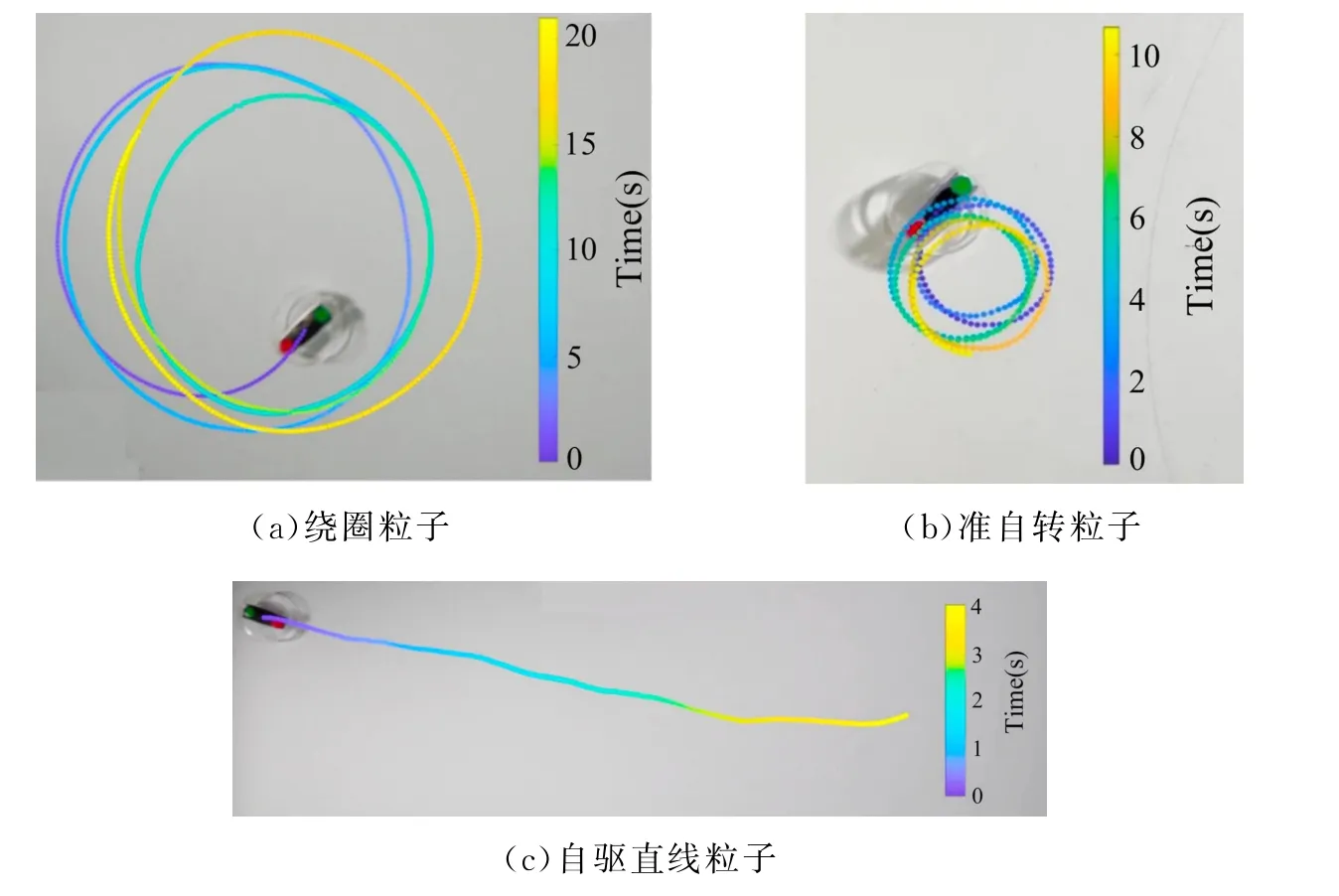
图2 不同活性粒子在平面上的典型轨迹Fig.2 Typical trajectories of different active particles
通过提取坐标进行计算,可以得到绕圈粒子和准自转粒子的旋转半径,对应于图2(a),该绕圈粒子的旋转半径r=13 cm,约为粒子直径的3倍。准自转粒子对应于图2(b),其旋转半径约为2.4 cm,仅为粒子直径的一半。我们通过随机抽样和多次重复实验,可以知道绕圈粒子的旋转半径约为粒子直径的3—4倍,而准自转粒子的旋转半径则不超过粒子直径的0.5倍。图2(c)为自驱动直线粒子的运动轨迹,其旋转半径可近似看成无穷大。
2 结果和讨论
我们将活性粒子放入高度为2 cm 的二维圆形容器。如前猜测,活性粒子的运动属性会影响受限空间内的粒子涡旋运动,同时粒子在容器内的堆积密度也会对集群行为产生显著影响。因此我们首先确定实验对象为同种运动模式的活性粒子,例如转圈顺时针粒子。在直径固定(D=60 cm)的圆形容器内,分别放入30、60、98个粒子,对应的堆积密度分别为ρlow=0.21,ρmiddle=0.42,ρhigh=0.68,使粒子的堆积密度经历低、中、高三个变化。我们在上述堆积密度使用不同运动属性的粒子观测活性物质系统的集群行为,并用摄像机拍摄实验视频。
完成实验后,利用MATLAB识别程序对视频进行图像处理和粒子追踪,将视频中的每1帧图片转化为二值图,再利用MATLAB 中的PIV 工具包(Particle image velocimetry,又称粒子图像测速法)识别粒子的瞬时流速场并求平均。通过比较不同实验条件下的平均流速场,分析活性粒子的涡旋行为的性质与转变。
当把一定数量的活性粒子放在二维受限空间中时,粒子不仅会受到环境边界的影响,粒子之间还存在着相互作用,多种相互耦合作用使活性粒子系统涌现出有趣的集群行为。我们根据旋转半径由小至大的顺序,先分析准自转活性粒子(逆时针旋转)的实验结果。在自转手性相同的情况下,逐渐增加粒子的填充密度,根据视频提取出相应的平均流速场。实验结果表明当准自转粒子以低密度填充时(ρlow=0.21),每个活性粒子基本在原地自转,粒子间很少发生碰撞作用,反映在平均流速场上,则代表流速方向的箭头排列杂乱无序,且代表大小的箭头长度很短,表明这种情况没有涡旋,瞬时流速经多次平均后几乎为零,如图3(a)所示。随着粒子堆积密度的增加(ρmiddle=0.42),活性粒子之间的碰撞频率也随之明显增加。反映在实验观察中,表现为可时常发现体涡旋,但涡旋寿命较短,一般只有秒量级,且涡旋在容器中四处运动,随时可能发生解体,这种瞬时涡旋的平均流速场与低堆积密度时类似,如图3(b)。当粒子高密度填充时(ρhigh=0.68),系统涌现出新的集群行为——拓扑保护的边界流,它可被视为一种特殊的涡旋。根据平均流速场的指示,在容器边界处存在鲁棒性很强的边界流,并且边界流速随着容器径向方向衰减,如图3(c)所示。拓扑边界流的物理机制源于准自转粒子之间碰撞频繁,造成粒子的非均匀空间分布,从而导致了空间非均匀的摩擦应力,摩擦应力耦合转子自旋使得粒子的自旋角动量转变成了粒子的集体角动量,最终形成拓扑保护的边界流[14,26]。
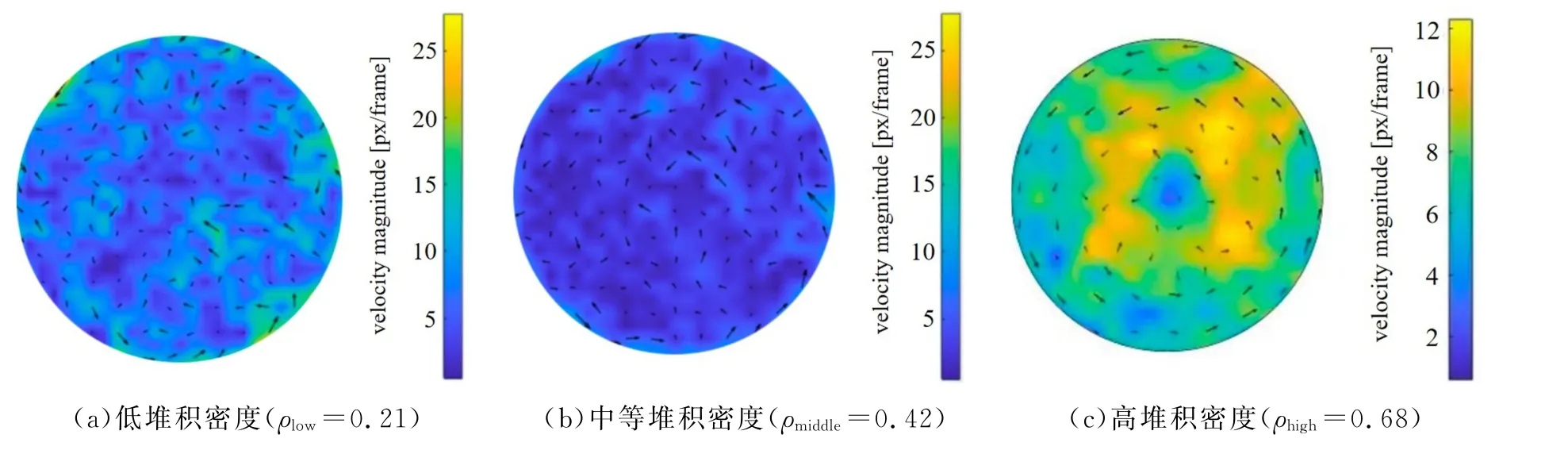
图3 逆时针准自转活性粒子在不同堆积密度时的平均流速场Fig.3 Average flow velocity fields of active particles with a counterclockwise quasi-spinning mode at different packing densities
顺时针准自转粒子的实验现象与图3中逆时针粒子的现象基本一致,除了拓扑边界流的流动方向相反。
对于绕圈逆时针粒子,其旋转半径远大于粒子直径。我们改变粒子在容器内的堆积密度,观察记录粒子在容器内的自发集群行为。当粒子填充密度为ρlow=0.21时,粒子之间碰撞就已经比较频繁,可形成寿命较为短暂,并且空间位置不固定的瞬态涡旋,视觉上涡旋会在容器中到处游走,粒子时聚时散,而反映在平均流速场上,则流速场内的箭头排列整体杂乱无序,因此低堆积密度下绕圈粒子系统既没有呈现出边界流,也没有稳定涡旋的存在,如图4(a)所示。当粒子中等堆积密度时,即ρmiddle=0.42时,时空上不稳定的涡旋会转变成相对稳定的涡旋,即涡旋一旦形成,在空间中只会围绕容器中心发生缓慢随机移动,而且寿命相对较长,几乎不会消失。这样,平均流速场仅在边界处箭头排列不甚规整,而涡旋中央的箭头则形成了相对完整的圆圈。这说明在容器中间会产生一个涡旋,但没有边界流,见图4(b)。我们发现当粒子高密度填充,即ρhigh=0.68时,涡旋最终演化成为稳定涡旋,这里稳定有双重含义,即粒子几乎填满整个容器,使得涡旋以容器中心进行整体旋转运动,在空间上几乎不再移动,而涡旋一旦形成,就不会消失,在时间上也稳定存在,对于这种稳定体涡旋,平均流速场中各层箭头首尾相连,排列规整,只有在涡旋中心处速度为0,参见图4(c)。体涡旋的形成是因为绕圈粒子在碰撞之后并不完全弹开,而是具有一定的取向,使粒子在碰撞后可以并排平行运动,由于粒子的密度较高,在粒子相互远离之前有其他粒子继续碰撞,使得平行运动的粒子集团不断增加。此外,绕圈粒子不但具有旋转特性,而且粒子具有自推进平动,从而形成体涡旋。我们改变绕圈粒子的手性,选用绕圈顺时针粒子重复上述实验,发现在不同填充密度下,除了涡旋旋转方向为顺时针,其他实验观察现象一致。这说明对于绕圈活性粒子,手性不影响容器中的涡旋行为的过渡转变。
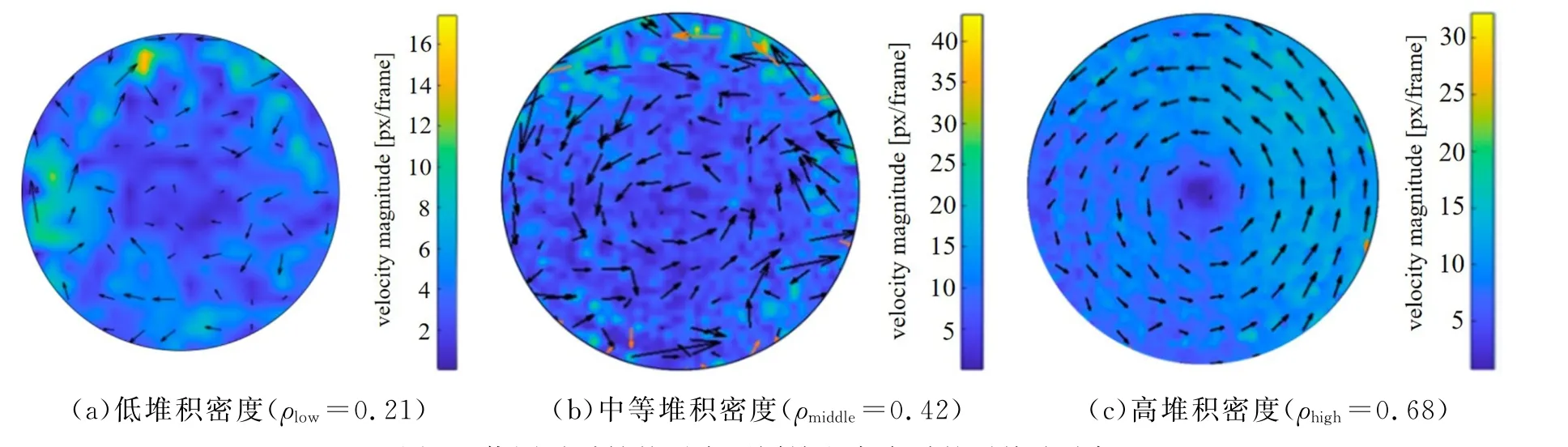
图4 绕圈逆时针粒子在不同堆积密度时的平均流速场Fig.4 Average flow velocity fields of active particles with a counterclockwise circle mode at different packing densities
最后我们分析自驱动直线粒子(旋转半径可近似看作无穷)的集群行为。当粒子填充密度ρlow=0.21时,绝大部分活性粒子会经过一系列的碰撞到达容器边界处,然后紧贴边界开始运动。这是因为活性粒子一旦碰撞边界,就需要一定时间转向离开,但转向之前只能沿着边界运动,这在以前工作中已有相关报道[27]。在我们实验中更为有趣的是,沿着边界运动的粒子之间依靠摩擦锁住了粒子的运动取向,使粒子群可首尾相连围绕边界长时间运动形成边界流涡旋,而容器内部位置几乎没有粒子。这里需要说明的是,边界流的运动方向随机,我们重复了多次实验,边界流顺时针和逆时针旋转的次数基本持平。但这种边界流并非集体效应的拓扑边界流,而更类似于粒子与边界相互作用的单体取向和粒子之间摩擦作用的混合结果。从平均流速场上看,边界处出现明显的环流箭头,如图5(a)所示。随着增加粒子堆积密度至ρmiddle=0.42,实验现象类似于低堆积密度的情况,只是围绕边界长时间运动形成的不再是单层粒子边界流涡旋,而是数层粒子形成的边界流涡旋,平均流速场如图5(b)所示。当进一步增加粒子堆积密度,即ρhigh=0.68,依然有边界流涡旋出现,其方向也是随机,偶尔粒子整体也会旋转,出现暂态体涡旋,其反映在平均流速场上,显示边界处具有环流,但沿着径向方向衰减,见图5(c)。

图5 自驱动直线粒子在不同堆积密度时的平均流速场Fig.5 Average flow velocity fields of self-propelled linear particles at different packing densities
根据以上实验现象,我们发现在低堆积密度时,随着从准自转粒子、绕圈粒子到自驱动直线粒子运动属性的变化,集群行为的演化从无规则运动转变为时空不稳定的瞬态涡旋,直至非拓扑边界流涡旋。而在中等堆积密度时,除了绕圈粒子的时空不稳定的瞬态涡旋转变为相对稳定的时空涡旋,运动属性对集群行为演化的影响与低堆积密度基本一致。当处于高堆积密度时,粒子几乎填充了整个容器,在粒子间相互耦合和粒子与边界相互作用下,集群行为的转变更加显著,演化从拓扑边界流涡旋过渡到稳定体涡旋,最后到达非拓扑边界流涡旋,总结见表1。

表1 不同条件下的涡旋行为Table 1 Various vortices at different conditions
3 结论
在本研究中,我们利用玩具机器人制成3种运动模式不同的活性粒子,研究粒子运动属性以及粒子堆积密度对在二维受限空间中活性粒子涡旋模式的影响。实验结果表明,改变粒子的堆积密度和运动属性,活性粒子系统展示了多种涡旋行为。在低中堆积密度时,随着旋转半径的增加,集群行为从瞬态涡旋开始过渡到相对稳定的体涡旋,最终形成非拓扑保护的边界流涡旋。而高堆积密度时,涡旋运动模式的转变更为显著,从准自旋粒子的拓扑边界流演变为时空稳定的体涡旋,直至最终的非拓扑边界流涡旋。与改变粒子的堆积密度相比,改变粒子的运动属性会带来显著涡旋模式转变。
我们可以使用外界激励控制粒子的运动性质,这为直接改变集群运动特性、实现多功能切换提供了新策略。例如可以将绕圈粒子转变为自转粒子,这样在高填充密度时体涡旋将转化为拓扑边界流,鲁棒性的拓扑边界流将能对悬浮于其中的非活性货物进行拓扑保护的输运[16],其中货物沿着系统边界单向、鲁棒地输运,并可以无散射地绕过障碍物。反之,高堆积密度下的绕圈粒子的振荡涡旋[18],也有潜力作为粒子振荡时钟应用在自驱动器件。

