基于多层面Rasch 模型的英语口试信度分析
邵 健
(浙江工商职业技术学院,浙江 宁波 315012)
0 引言
英语分级考试是较为常用的测试手段之一,目的在于区分学生的语言水平,从而开展分级分层教学,该方法被很多高校采用[1]。但鉴于操作层面的原因,分级往往“以总分为标准”,无法区分读写能力和听说能力的差异,从而导致最终听说、读写技能发展不均衡[2]。因此,综合考虑听说读写四个技能的分级考试,才能较好地反映学生的真实语言水平。本研究以某校英语分级考试中的面试型口试为研究对象,该测试属于语言运用测试的一种常见形式。它不仅考察学生的语言知识、语言运用和交际技巧,同时对学生的心理素质也有一定要求,整体难度较高。更重要的是,口试涉及主观评分环节。评分员需要凭借自己的经验、知识及对评分标准及量表的理解和把握,对考生的表现进行观察、理解和评判[3],考生实际水平和能力往往受到评分员、评分标准和量表等因素的影响。由于人为要素所造成的误差是始终存在、且难以避免的[3-7],这对测试信效度的保障提出了更高要求[8]。
为了更精准评估考生英语听说能力,剥离考生能力之外的其他影响因素,本文运用多层面Rasch模型(MFRM)分析这次英语口试质量,期望达成以下目的:(1)通过对考生层面的分析,对考生成绩进行微调和补偿,最终确定其分级;(2)对评分员效应以及评分员层面与其他层面的交互作用进行检验,并反馈评分员以提高评分准确性;(3)以MFRM 模型对该校现行英语分级考试评分质量进行总体检验。
1 多层面Rasch 模型
Rasch 模型是项目反应理论经典模型之一,相较于经典测量理论,它以 “概率函数的形式来描述项目作答反应结果是如何受到被试能力水平和项目特性联合作用的影响”[9]4。该模型克服了经典测量理论中观察分数等权重线性累加的弊端以及测量误差计算的不精确性,可以更精确地估算考生实际水平和项目的计量学参数。Rasch 模型可分为单参数、双参数及三参数模型,从考生和题目两个层面进行分析。但实际测试环境中,特别是进行主观题类评分时,评分标准、评分量表、评分员及其对评分标准的理解、把握和运用均有可能造成测量误差和偏差。因此,李纳克尔(Linacre)在经典Rasch 模型的基础上提出了多层面Rasch 模型[10],将经典模型无法企及的层面要素纳入其中,从而拓展了模型的解释效力,对考生得分概率的评价更为全面。详细介绍可参考张洁[11]和李久亮[12]的相关研究。目前,国内学界将多层面Rasch 模型运用于大型主观测试(如写作和口语)的信效度检验[13-14]及评分员效应和评分质量分析[5,11,15,16],取得了良好效果,现有研究表明,该模型可有效用于检验主观测试的质量,模型信息可反馈给施测部门、评分员和教师,进而反拨教学。
2 研究设计
2.1 数据来源及口试说明
数据来源于某校中外合作专业三个班新生(n=141)的英语分级考试成绩。该考试参照雅思,分为阅读、写作及口试三个部分,研究仅分析口试成绩。口试分为三部分,用时10-15 分钟。第一部分为热身环节,回答诸如姓名、年龄、家乡等问题;第二部分为简答题,要求学生用2-3 个句子予以回答;第三部分为讨论题,要求学生结合某个主题阐述自己的观点、见解或想法等,并就其展开论述。评分标准为国际第二语言水平量表 (International Second Language Proficiency Ratings,简称ISLPR)。评分者需要根据考生在口试过程中表现出的英语准确性、流利度和得体性进行评价,分别给出听和说的成绩。
口试在封闭教室中进行,每次仅有一名考生进入。考试由一名外籍教师负责提问、引导和互动,全体评分员对该考生的听说表现进行打分。量表分为6 个主要级别(记为0-5),加上主要级别之间的过渡级别(记为0+,1-,1+,2+,3+,4+),共计12 个级别(由于多层面Rasch 模型软件只能处理连续型数值变量,因此要求口试的原始成绩按照级阶被转化成连续型数值。)。按照该校中外合作专业语言阶段的规定,考生得到2+就可以升入专业学习,所以在实际分级考试中,只需用到前5 级进行评分。在测试前,所有评分员都参加过澳方组织的培训,并获得澳方颁发的TAFE 资格证书。此外,为了弱化评分员个体的差异,在测试中共计安排了四位评分员,其中1 号和2 号为中方教师,在中外语言项目任教年数都有十余年,3 号和4 号为外籍教师,任职年限分别为7 年和2 年。
2.2 MFRM 建模
采用李纳克尔开发的Minifac 软件 (V3.80.0)建模,该软件是Facets 的学生版本,除分析样本数量上限为2000 条外,其他均与正式版本无异。
所用MFRM 建模包含以下几个层面:考生的听说能力、评分人和评分标准,所构建的数学模型如下:Log(Pnijk/Pnij(k-1))= Bn-Ci-Dj-Fjk,其中,Pnijk和Pnij(k-1)分别表示第n 个考生在第j 个评分标准上被评分员i 判定为k 分和k-1 分的概率;Bn为第n个考生的能力;Ci是第i 个评分员的评分严厉程度;Dj是第j 个评分标准的难易度;Fjk代表第j 个评分标准中相邻分数段对应的阶梯难度。
通过MFRM 模型的统计分析,可综合考察学生能力、评分员、评分标准及量表如何在共同作用下影响学生的最终成绩,对评分过程中产生的各种测量误差、以及各个层面交互作用产生偏差的原因进行诊断,从而对考生的最终定级提供修正和补偿,最终提高英语口试质量。
3 统计结果及讨论
3.1 总体分析
图1 为模型总层面图,展示了所有层面的总体情况,估算结果被统一在第一列的共同单位洛基值上。该值已经进行了对数转换,满足线性和等距特征,因此可以直接进行跨层面的估算和比较。第二列是考生能力值,每个星号代表2 名考生。从星号数量可以看到,考生的能力并未呈现较为理想的正态分布,考生能力之间差异较大,能力最强的考生和能力最弱的考生之间相差22.5 个洛基值。第三列是考官严厉程度,最严考官为j1,最松考官为j2,两者之间相差3 个洛基,约为考生能力跨度值的七分之一,因此,考官个体的严格与否不至于对最终评价产生决定性的影响[17]。第四列是评分标准,即听和说的总体评价分,两者差距大约1 个洛基。第五列为评分量表,分值之间的间隔横线为相邻分值的临界线,下图中各个分数之间的分割范围有密有疏,所包含的洛基值不等,从侧面上证明评分员对分值的把握较好,评分主要依据为考生能力。总体而言,评分员和评分标准之间的差异不大,但考生能力之间确实存在较大差异。

图1 模型层面图
3.2 层面分析
MFRM 模型能对每个个体和层面进行运算和估值,提供更多评价信息,对测试进行质量检验,帮助修正测评误差,反馈评分质量,为分级教学提供依据。下文将对各层面逐一展开分析。
3.2.1 考生层面。表1 提供考生层面数据。表下面数值是考生层面总体估算值,分隔比率为5.61,即考生之间的差异是测量误差的5.61 倍;分隔指数[根据Myford & Wolfe(2004),分隔指数计算公式=(4* 分隔比率+1)/3]为7.81,即考生差异可分为7.81 个层次。结合卡方值及统计决断(X2=4388.6,p=.00),可判定考生之间存在显著差异。表1 包含考生序号(第一列),测量值和测量误差(第二至第五列) 和统计拟合指标(最后四列)。其中obsvd Ave.和Fair(M) Ave.分别对应学生实际得分( 均值)和学生期望得分(均值),后者是模型综合评分员严厉度、评分标准难度和评分量表所输出的理想分数,和前者相比,它更接近考生实际能力。有学者[13,18]提出,可以根据两者差异调整学生成绩,对最终的报道等级进行微调和补偿。本文计算了两者之间的差值,发现取值在正负0.05 之间,均值为-0.00511,标准差为0.034732,因此无需进行调整。
表1 中还包含数据和模型的拟合情况,具体指标为加权和未加权均方拟合统计量(Infit MnSq和Outfit MnSq)以及它们的Z 标准分。李纳克尔认为,未加权均方拟合统计量往往受到个体差异大的数据影响,因此,实际操作中往往以加权均方拟合统计量为准,其取值在0.6 至1.5 之间时可认为数据和模型拟合较好[19]272。也有学者根据实际估算的参数数量建议将评判指标放宽到0.5至3 之间[13]。结合本次研究的评分员和评分标准的数量,我们将拟合值锁定在0.5 至2.5 之间,大于2.5 属于非拟合(misfitting),即考生的实际观测值和模型预测值之间差异过大,小于0.5 则是过度拟合(outfitting),即情况刚好相反。表1 包含所有拟合不良的考生,共有3 名考生的Z 分大于等于2.5,属于非拟合。另有18 名学生数据过度拟合,占比12.77%。鉴于85.1%学生(120 人)的数据拟合良好,可认为考生数据整体拟合具有内部一致性。
3.2.2 评分员层面。评分员是测试中的关键层面,也是最容易出现测量误差的层面。主观上看,评分员的个体因素,如人生经历、个人偏好、情感认知、喜好习惯等,均能影响其判断,而且评分员对评分标准的理解和掌握也因人而异,存在不同;客观存在的冗长无趣的评分过程以及在评分过程中可能存在的分神、疲倦等原因,都有可能形成评价误差。因此,即便在考前对评分员进行培训,在实际测试过程中,仍可能存在和考生实际表现并无关联的测量误差,即评分员效应[20],包括严厉度、晕轮效应、集中趋势、随机效应和区分性这五个方面[3,4]。
表2 包含测量值、拟合指标和层面总体估算结果。评分员层面的分隔比率为7.91,分隔指数为10.88,这意味着四个评分员的打分严厉度可以分为将近11 个不同的层次,结合卡方检验的结果(X2=236.3,p=.00),可以认为评分员的严厉度之间存在着显著差异。从评分员之间的差异看,一号评分员的打分最为严格,二号打分最为宽松,但尽管四位评分员的严厉度之间存在显著差异,但是,从他们的点二列相关系数看,相关度在0.87 至0.89 之间,总体较为理想,所以可以认为,评分员打分的严厉度虽然不一,但评分的一致性和可靠性较高。

表2 评分员层面
此外,可通过加权均方拟合统计量评判评分员打分的一致性问题。对于该指标的临界值,一般有两种看法,一种是以加权均方拟合统计量的平均值和标准差作为标准,以平均值加减两个标准差(M+/-2SD)作为上下限[21]117;另一种以加权均方拟合统计量取值在0.7 至1.3 为限,但也可以适当放宽至0.6至1.5 之间[22]。表2 中四位评分员的加权均方拟合统计量均在临界值内,评分员一致性较为理想,评分员不存在光环效应[3,4]。综上,可以认为评分员具有较好的内部一致性,评分结果总体可信。
3.2.3 评分标准层面。评分标准分为听和说两部分,表3 显示,分隔系数为5.32,信度为0.93,卡方检验结果显著(X2=29.9,p=.00),即两者存在显著差异,评分员能有效使用评分标准区分考生听说能力。数据显示,评分员在第二项标准上更加严格,两者相差0.78 个洛基单位。经过访谈,笔者发现,相对于听的能力,对说的评判更加直观。按一位中方评分员说法,考生的发音、语调、语法、以及语言产出的量,都是直观可见的。而对于外教而言,评判一个考生口语产出的质和量,更是有着本族语使用者的优势。因此,和内隐的听力相比,对说的评判就显得更加严格。

表3 评分标准层面
从拟合指标看,这两项标准均在可接受范围内(M+/-2SD),说明评分标准的前后一致性较为理想。但是,“说” 的加权均方拟合统计量小于1,Z 分绝对值刚好为2,说明该标准的区分层次比预期要少,评分员可能过多地使用了某一分数段,提示存在晕轮效应,这有两个原因,一是考生水平确实较为集中,彼此差距不大;二是评分标准不够细致,不能很好地区分考生水平[16]。结合口试的实际情况,笔者认为两者兼有。一方面,报考该校中外合作专业考生的整体英语水平较弱,但特别差和相对较好的学生数量少,主要集中在ISLPR 体系中2 分的能力水平上;另一方面,所用评分量表共计5 个级阶(0-4分),量具间隔为1,因此,对大多数的考生而言,只能用2-3 个级阶来进行评价,无形中加剧了评分分值集中。
3.2.4 评分量表层面。评分量表层面反映了评分员是否有效使用评分量表,量表中分数段对考生能力的区分和体现等[22]。表4 反映了评分量表层面的质量和分数段标定。从平均测量值可以看出,分数段从低分到高分呈现出正态分布,且不同分数段之间存在一定的间隔,说明评分员能较为准确地运用量表来区分考生的水平。一般认为分数段之间理想间隔应该为1 至4 个洛基单位,否则提示可能存在评分的集中趋势[23]。从各分数段的起始值看,2-3分的间隔在理想范围之内,但是1-2 分,3-4 分之间则超出了间隔上限。这提示评分员过多使用了2 分和3 分段的量表,评分上存在一定程度集中。事实上,2 分和3 分段的使用频次是最高的,占所有分数段的75%。这与前文 “说” 的评分标准区分度不高,打分相对集中的结论互为印证。事后对评分员的访谈发现,评分标准和量表对考生听说能力的划分并不是十分细致,在实际打分环节,评分员所能用的分值基本只有2 到3 个。评分量表能满足对考生的分级要求(即语言初级、中级、高级班划分),但对于同级别考生之间的进一步细分就显得捉襟见肘。

表4 评分量表层面
从未加权均方拟合统计量看,量表不同分数段除0 分外,其他分数段的一致性还是较为理想,取值基本在1 左右,全部分数段均未超过2的上限[23],因此,量表还是能够较好地反映考生的能力水平。
量表质量还可通过量表分数段的概率曲线图(图2)进行分析。图中的X 和Y 轴分别代表相对于题目难度的考生能力和考生得到某个分值的概率,从左至右的五条曲线分别代表0 到4 分五个分数段的概率,曲线与曲线的交叉点就是相邻分数段之间的临界点。帕克(Park)提到,概率曲线之间需要有一定的间隔,且每个曲线需要有自己的独立峰顶,能力值处于峰顶的考生得到该分数段的概率最高[24]。图2 中每个分数段都有自己独立的峰顶,分值从左至右排列且呈现单向递增趋势。另外,曲线之间的间隔也相对较小,并不是分得很开,而后者恰恰是集中趋势的表现[4]。综合起来,可以认为,虽然在部分分值上存在集中趋势,但量表层面的总体可信度较高。
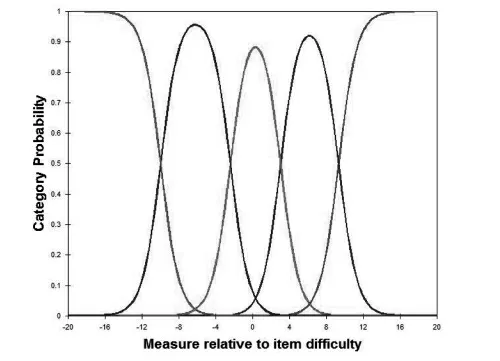
图2 分数段概率曲线
3.3 偏差分析
MFRM 还可以分析各层面的交互作用,特别是用于评分者层面与其他层面之间的相互作用关系[15],从而区分、界定评分员效应中因随机因素所造成的误差和系统偏差。通过对评分员评分前后不一致现象的分析,可以反馈给评分员,并提高测试质量[7,13,14,16]。结合口试中评分员的重要作用,本文对评分员层面与其他层面之间的交互作用进行了偏差分析,结果如下表5。以t 值绝对值是否大于2 为显著偏差的评判指标,大于2 说明评分员过于严格,小于-2 则过于宽松。
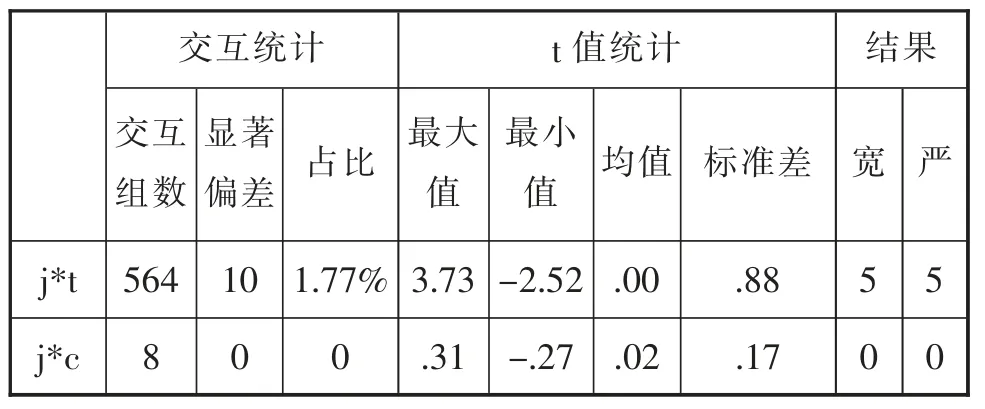
表5 评分员和其他层面交互结果汇总
表5 显示,考生和评分员共计有564 例(141*4)交互组数,其中t 值大于2 和小于-2 的各有5 组,共计出现了10 例显著偏差,占比1.77%,小于5%的临界标准[21]149,而评分标准和评分员之间共计8 例(2*4)交互组数,其t 值在-0.27 至0.31 之间,不存在显著偏差,层面的交互作用不显著。这说明评分员对标准的把握较好,一致度较高。
表6 为评分员和考生层面之间的偏差分析。该表显示,出现偏差数最多的是4 号评分员,最少的是3 号。2 号和1 号居中。结果和评分员的经验与国籍有关,4 号是新外教,任职2 年,经验相对不足。3号评分员自2008 年开始就开始在中外语言项目中任教,一直从事写作和听说教学,经验相对丰富。而1 号和2 号评分员都是中方教师,从教学经验上看不逊于外籍教师,但是,在语言敏感性上终归是稍逊一筹。

表6 评分员和考生显著偏差表
从考生能力值看,出现偏差最高的是中间段考生,能力值位于-3 到5 个洛基单位之间(可结合图1),对于这些考生,出现了5 例过严打分,4 例过于宽松打分,另有1 列宽松打分出现在能力值相对较高(6.27 个洛基单位)的39 号考生身上。在中等程度学生中容易出现偏差的现象与其他学者的研究相吻合[13,25]。但是,本次研究没有发现Congdon & McQueen[26]和戴朝晖、尤其达[15]所提到的评分时间稳定性问题,出现偏差的考生和他们考试时间无关。
另外,编号为56 的考生处于评分员打分过严的范畴,同时,该考生的个体统计量也曾出现过非拟合现象(表1 第三行数据),可以认为对该生的打分确实存在问题,可以考虑进行复核。但是,在检验其能力水平及测量预期分均值后,还是认为该生的最终报道等级无需调整。
4 结论
本文运用MFRM 模型,从多个层面对某校中外合作专业新生分级口试成绩进行信度分析,结合各层面及层面之间分析的结果,认为此次测试总体质量较好。
首先,考生层面的分隔比率和信度较为理想,根据分隔指数,可以将考生分为大约8 个不同的层次,而分级考试只要将学生分为三个级别,因此,分级口试是有效的。虽有3 名考生(2.13%)出现了非拟合,18 人出现了过度拟合情况,但经复查这些考生的实际得分和预期得分后,无需对其报道等级进行调整。其次,评分员层面的分隔指数、信度及卡方分析结论都提示,虽然评分员严厉度之间存在着显著差异,但四位评分员的加权均方拟合统计量均在临界值内,可以认为评分员具有较好的内部一致性,评分结果总体可信。事实上,绝大多数MFRM 对评分员层面的分析都得出了类似的结论[5,7,13,16],即评分员宽严度之间存在差异,但评分员的内部一致性总体理想。再次,评分标准之间存在显著差异,但同样具备一致性结论,评分员能有效运用听说两个标准对考生进行有效区分。此外,“听” 和 “说” 两个评分标准的加权均方统计拟合量在0.7 至1.3 之间,这证明标准之间的关联性适当且又不过度[17]。在评分量表上,虽出现两个分数段的集中趋势,但其他结果表明量表层面总体可信度较高。
然而,本次口试中还发现了一些亟待解决的问题,主要体现在考生的质量和评分量表的度量两个方面。从考生层面看,大多数学生的口语能力居中,没有特别好或者特别差的学生,从分布形态看,属于中间大两头小;从评分量表看,共计0 到4 分五个级阶,按照ISLPR 的评分标准,0 分标准为零基础学生,4 分标准为本专业经过1-3 个学期语言训练后达到的最终能力水平,因此,对于大一新生而言,除极个别个体外,绝大部分考生的口语测试成绩为1至3 分。这就造成了中间分数段的集中。而考后对评分员的访谈也发现,现有评分标准和量表适用于分级这一 “粗粝化” 的分级目的,但无法实现对同级别考生听说差异的 “精细化” 描写,因此,有必要对评分标准和量表进行进一步细化,以便在后期实现班级内部的差异化教学。分析还发现,评分员在本专业的任职年限和经历确实会影响最终评分质量,造成偏差,因此,在常规考试培训之余,还应给予更多的实践操练,以帮助新进教师适应本专业的评价体系。
总之,应用MFRM 方法可以更加有效、科学地评价主观性考试中影响考生成绩的诸多因素,将人为的测量误差剥离出来,通过对测量值的修正和补偿,最大可能地反映考生的实际能力。此外,对评分员、评分标准及量表的分析,能够全面综合诊断、动态监控评分员的评分过程和评分结果,从而反馈评分员本人,对提高评分质量及后期评分员培训都有实际借鉴意义。

