2022年新高考Ⅰ卷第12题的课本溯源与变式探究

康俊太

(甘肃省广河县三甲集中学,甘肃 兰州 731301)

高考题源于课本,而高于课本,但“源于”有时是显性的,容易被发现,有时却是隐性的,需要进一步探究才能发现.笔者主要从显性与隐性两个视角来探究2022年新高考Ⅰ卷第12题的课本溯源,最后给出该高考题与课本习题的变式探究,设法实现从新教材到新高考的过渡.

1 高考真题

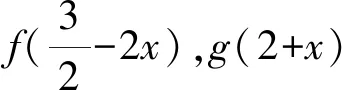
C.f(-1)=f(4) D.g(-1)=g(2)

因为(f(x)+C)′=f(x),所以f(x)的图象经过上下平移后,其对称性与导函数的性质不发生改变,即f(x)+C也满足题意,所以不能确定f(0)=0,故选项A错误.

2 试题评析

试题考查了考生分析问题和运用函数、导数相关知识解决问题的能力.作为新高考试卷的压轴选择题,试题紧扣课程标准,力图引导教学,符合基础性、综合性、应用性、创新性的考查要求.试题将导函数与函数的性质结合,设计新颖,具有较好的选拔功能.

以往试题中考查抽象函数性质的问题,往往通过特殊值法、单调性、奇偶性即可得出结论.试题创造性地将导函数引人其中,这便成为本题的一大亮点.同时多选题的题型设置也为不同能力层次的考生提供了发挥的空间.试题源于教材,紧扣课程标准,对考生的能力能进行很好地区分,具有较好的选拔功能.

3 题后反思

本题作为选择题,我们可以巧做.取符合题意的特殊函数f(x)=sinπx+1,便可迅速利用排除法得到正确选项,这就是解法2的思想.

而解法1是按照解答题的要求来做的,这样的好处就是很好地揭示了问题的本质:(1)函数的奇偶性、对称性和周期性的关系;(2)函数与其导函数的对称性的关系.

一般地,若函数f(x)具有奇偶性和对称性,则f(x)必有周期性;若函数f(x)具有奇偶性和周期性,则f(x)必有对称性;若函数f(x)具有周期性和对称性,则f(x)必有奇偶性.其结论总结如下:

(1)若f(x)是奇函数且满足f(a+x)=f(a-x),则f(x)的图象关于直线x=a对称且最小正周期T=4a.

(2)若f(x)是偶函数且满足f(a+x)=f(a-x),则f(x)的图象关于直线x=a对称且最小正周期T=2a.

(3)若f(x)是奇函数且满足f(a+x)=-f(a-x),则f(x)的图象关于点(a,0)对称且最小正周期T=2a.

(4)若f(x)是偶函数且满足f(a+x)=-f(a-x),则f(x)的图象关于点(a,0)对称且最小正周期T=4a.

4 课本溯源

函数的对称性与奇偶性的关系,不是什么新的内容,因为它是源自课本习题.

2019年人教A版《数学必修第一册》第87页第13题如下:

我们知道,函数y=f(x)的图象关于坐标原点成中心对称图形的充要条件是函数y=f(x)为奇函数,有同学发现可以将其推广为:函数y=f(x)的图象关于点P(a,b)成中心对称图形的充要条件是函数y=f(x+a)-b为奇函数[2].

(1)求函数f(x)=x3-3x2图象的对称中心;

(2)类比上述推广结论,写出“函数y=f(x)的图象关于y轴成轴对称图形的充要条件是函数y=f(x)为偶函数”的一个推广结论[3].

解析(1)解法1 设函数f(x)=x3-3x2的对称中心为P(a,b),则y=f(x+a)-b=(x+a)3-3(x+a)2-b为奇函数.

解法2 因为函数y=f(x+1)+2=(x+1)3-3(x+1)2+2=x3-3x是奇函数,由题意知函数f(x)=x3-3x2图象的对称中心为(1,-2).

(2)略.

5 习题探究

该高考题还涉及导函数与其原函数的对称性之间的关系,虽然这道课本习题没有直接涉及导函数与原函数的对称性之间的关系,但通过进一步探究习题,可以获得这方面的知识.

本习题提到了三次函数的对称中心,经过探究发现,三次函数的对称中心有如下性质.

6 变式探究

变式1 设f(x)是定义在R上的奇函数,若f(x+2)为偶函数,则f(1)+f(2)+…+f(2024)=____.

解答案:0.

方法1因为f(x+2)为偶函数,所以f(x+2)=f(-x+2),又f(x)是定义在R上的奇函数,因此f(x+4)=f(-x)=-f(x),f(x+8)=-f(x+4)=f(x),即f(x)的最小正周期T=8.由题意知f(0)=0,得f(4)=0,f(8)=0.又f(5)=f(-3)=-f(3),f(6)=f(-2)=-f(2),f(7)=f(-1)=-f(1),所以f(1)+f(2)+…+f(8)=0,从而f(1)+f(2)+…+f(2024)=0.

方法2因为f(x+2)为偶函数,所以f(x)的图象关于直线x=2对称,又f(x)的图象关于原点对称,所以f(x)的最小正周期T=4|2-0|=8. 下同方法1.

A.f(2)=0 B.f′(1)=f′(0)

C.f(3)=f(2) D.f′(2022)=-f′(-1)

解选ACD.由题意知f(2-x)+f(2+x)=0,所以函数y=f(x)的图象关于点(2,0)中点对称.对f(2-x)+f(2+x)=0两边求导,得f′(2+x)-f′(2-x)=0,即f′(2+x)=f′(2-x),所以函数y=f′(x)的图象关于直线x=2对称.

对A,由f(2-x)+f(2+x)=0,令x=0,得f(2)=0.A正确.

综上,选ACD.