机械密封中Ω形和U形波纹管的疲劳寿命分析

李乾坤，李学旺，赵春雨，向 勇，刘宝龙

（明阳智慧能源集团股份有限公司，广东中山 528400）

0 引言

机械密封因其泄漏量小、使用寿命长、工作性能可靠而广泛应用于各个领域[1]。波纹管是机械密封中主要的部件，是有波纹且轴对称的管状壳体，在不同的作用力下可以产生较大的位移，具有较好的弹性补偿性能[2]，波纹管的使用寿命直接影响了机械密封的工作状态，从而影响设备的正常运转。疲劳是设备失效最主要的原因之一，需要对关键零部件进行可靠性和使用寿命的预测，检测及预防设备故障造成经济损失[3-4]。因此对波纹管疲劳寿命的分析可以更好地提高设备的运转性能。

金属波纹管的疲劳寿命计算一般都是采用EJMA 标准中的经验公式[5]，但由于实际工况的复杂性，计算结果的误差较大。赵文元、刘进祥等[6-7]采用热-结构耦合对焊接金属波纹管进行疲劳失效分析；吴媛媛[8]对金属焊接波纹管进行建模，网格划分以及静力学分析，得到变形和应力的分布云图，并计算疲劳寿命；秦建等[9]对无加强U 形波纹管进行疲劳寿命的公式推导，并且对比了奥氏体不锈钢和钛两种材料所制成波纹管的区别；Wu Jianguo、徐中华等[10-11]分别用有限元、实验和公式计算的方法分析了S 形波纹管的可靠性和寿命。本文通过建立波纹管三维模型，结合静力学和Miner 疲劳损伤理论，使用NCode对Ω 形和U形波纹管进行疲劳寿命分析，得到了发生疲劳失效的位置，预测了不同预应力下发生疲劳失效的循环次数。

1 Ω形和U形波纹管静力学分析

两种波纹管的几何尺寸如图1所示，尺寸参数如表1所示，L3为Ω 形波纹管圆环开口，L1为波距，L2为直边长度，W为波高，R1为波峰半径，R2为波谷半径，T为壁厚，单位均为mm，波根外直径为55 mm；r1为U 形波纹管波峰半径，r2波谷半径，H1为壁厚，H2为波高，单位均为mm，波根外直径为55 mm。波纹管材料为1 Cr18Ni9Ti，其弹性模量E=196 GPa，泊松比μ=0.3，密度ρ=7.9×103kg/m3，屈服极限σS=257 MPa，弹性模量EP=247 MPa。工作状态下，波纹管外表面受到0.6 MPa 的压力，主轴转速为1 000 r/min，根据文献[12-13]，计算两种波纹管的子午向薄膜应力和弯曲应力，均可满足使用要求。

表1 波纹管尺寸参数

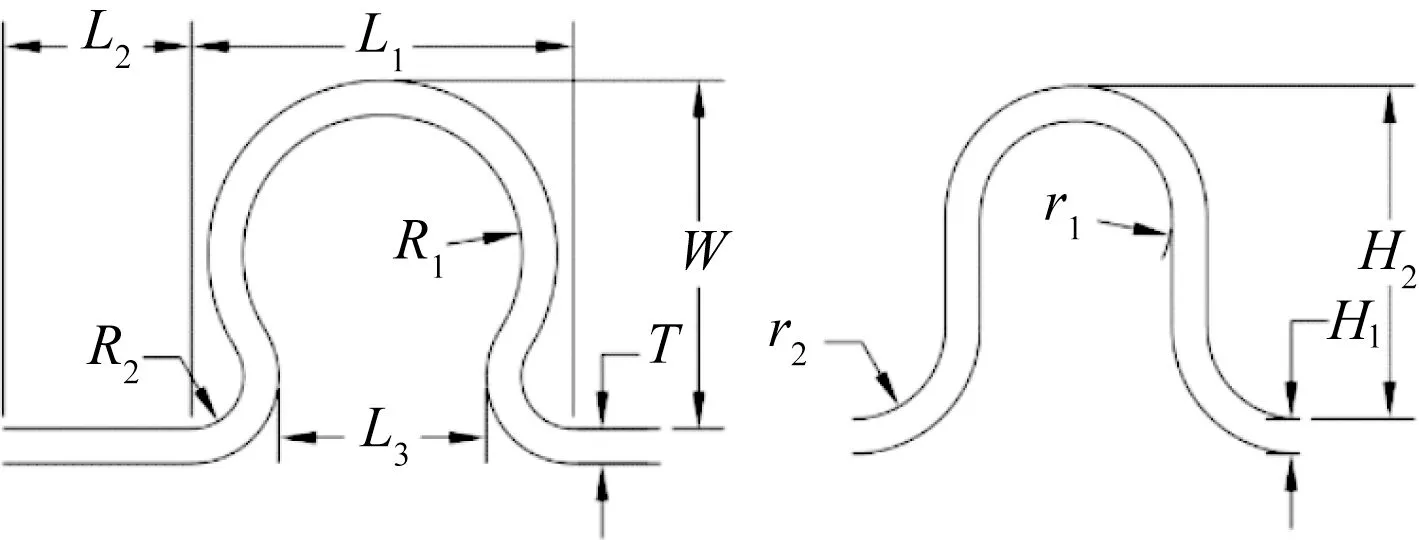
图1 波纹管基本尺寸

计算疲劳寿命前，需要对模型进行静力学分析，确定发生疲劳失效的位置。两种波纹管的网格划分如图2所示。NCode 进行疲劳寿命分析是以网格节点为计算对象，有多少节点就会有对应数量的疲劳寿命计算数据，为减少计算量都采用以6 面体主导的网格划分方法，Ω形波纹管共有621 824 个结点，95 424 个网格，U 形波纹管共有个755 526结点，116 394个网格。

图2 两种波纹管的网格划分

机械密封中大多都采用一端固定，一端自由的约束方式，本文采用此种约束方式，这里主要分析两种波纹管在轴向变载荷作用下的疲劳损伤，不考虑波纹管所受密封腔内的压力。在自由端分别施加30、50、70、90 N的预应力，方向沿轴向指向固定端。以预应力为50 N 时为例，两种波纹管的等效应力云图如图3 所示，在压缩预应力的作用下，两种波纹管应力集中都发生在波峰和波谷的位置，也是波纹管疲劳寿命最短的位置。

图3 预应力为50 N波纹管等效应力云图

分别对Ω 形波纹管和U 形波纹管在不同的预应力下进行等效应力分析，靠近受力端的波纹等效应力大，易发生疲劳损伤，第一波靠近受力端的距离不同，以靠近自由端的第二波为研究对象，提取从波谷到波峰不同位置的等效应力，提取位置如图4所示。图5为两种波纹管在不同预应力下，波谷到波峰的等效应力。应力集中都发生在波峰和波谷位置，Ω 形波纹管由于两个波谷之间有一段延长，波谷应力比波峰应力大；U 形波纹管波谷处的应力大于波峰，但相差不大；随着预应力的增加，两种波纹管的等效应力都呈现递增趋势。

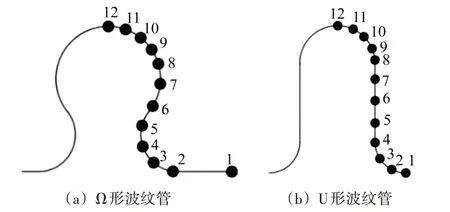
图4 两种波纹管提取应力位置

图5 不同预应力下两种波纹管波谷至波峰等效应力

以预应力为30 N 时为例，对比分析两种波纹管等效应力的分布及大小，图6 为预应力30 N 时，两种波纹管波谷至波峰各处的预应力。在波谷附近，由于Ω 形波纹管两波谷之间相距较远，过度平顺，因此波谷预应力相对U 形波纹管较小，而Ω 形波纹管波峰附近的等效应力大于U 形波纹管。任宁等[14]通过对Ω 形和U 形波纹管对比分析得到了波纹管的波峰与波谷相接处、波谷与直边段过渡处等结构不连续区存在明显的应力集中的结论，与上述研究结果一致。

图6 两种波纹管等效应力

波峰和波谷是应力集中的位置，易发生疲劳失效，以波峰为例，对比分析两种波纹管的等效应力，如图7所示，两种波纹管在靠近受力端处的波纹等效应变较大，随着预应力增大，等效应变增大；相同预应力下Ω 形波纹管受直边影响，两端等效应变减小明显；U 形波纹管类似弹簧，两端等效应变较大，中间波纹变化不明显。

图7 不同预应力下两种波纹管波峰等效应变

2 Ω形和U形波纹管疲劳寿命分析

2.1 Miner累计疲劳损伤

使用范围最广的两种疲劳分析的数学模型是S-N曲线模型和Palmgren-Miner 累计损伤模型，S-N曲线的数学模型如式（1）所示[15]：

式中：Nf为疲劳寿命；S为应力大小；A为疲劳强度；m为S-N曲线。

Miner线性累计损伤模型对损伤的定义是工作状态下零件受到总的循环次数和给定任意应力的时零件失效的循环次数之比，如式（2）所示：

式中：D为累计损伤；n为标准工况下的循环次数；Nf为给定任意应力时，出现失效的循环次数。

对于多应力下的疲劳损伤由式（3）表示，

式中：D为总的累计疲劳损伤；Di为在第i个应力下的累计损伤；ni为标准工况下的循环次数；Nfi为在第i个应力下，出现疲劳失效的循环次数。

联立式（1）～（2），可得到修正后的Miner 累计损伤模型，单应力下的Miner累计损伤如式（4）所示：

式中：C为疲劳强度的倒数。

多应力下的Miner累计损伤如式（5）所示：

式中：为S-N曲线为m时，第i个应力。

2.2 Ω形和U形波纹管疲劳寿命

将Ω 形和U 形波纹管在压缩状态下产生的最大主应力作为波纹管的子午向薄膜应力，结合修正后的Miner累计损伤模型和材料的SN曲线，通过NCode 进行疲劳分析，采用时间序列分析，生成2 s 的随机载荷，时间载荷如图8 所示，在2 s 的时间内生成100 个载荷点，这里以预应力为30 N 为例，每个时间对应的极值点反映载荷的大小，极值为负表明波纹管处于拉伸状态，为正值则处于压缩状态，极值大小反映了载荷大小，应力变化范围在-30～30 N 之间。采用随机时间序列而不采用周期时间序列，可以加快波纹管疲劳失效，缩短分析时间。

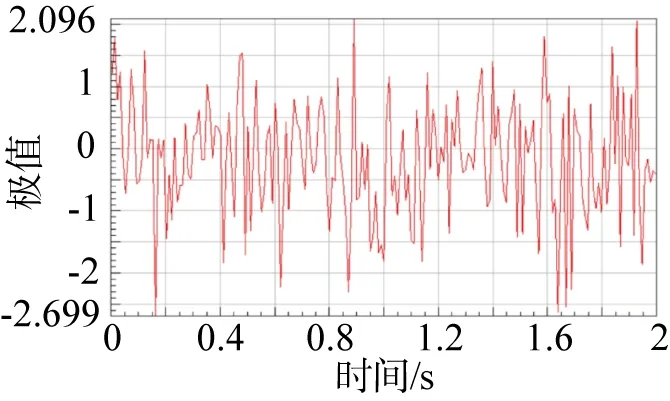
图8 随机时间序列

对Ω 形波纹管的621 824 个结点和U 形波纹管的755 526个结点进行疲劳计算，分别对不同预应力下的波纹管最大主应力和疲劳寿命（以循环次数表示）进行分析，Ω 形波纹管和U 形波纹管的最大主应力和疲劳失效循环次数分别如图9、10所示。

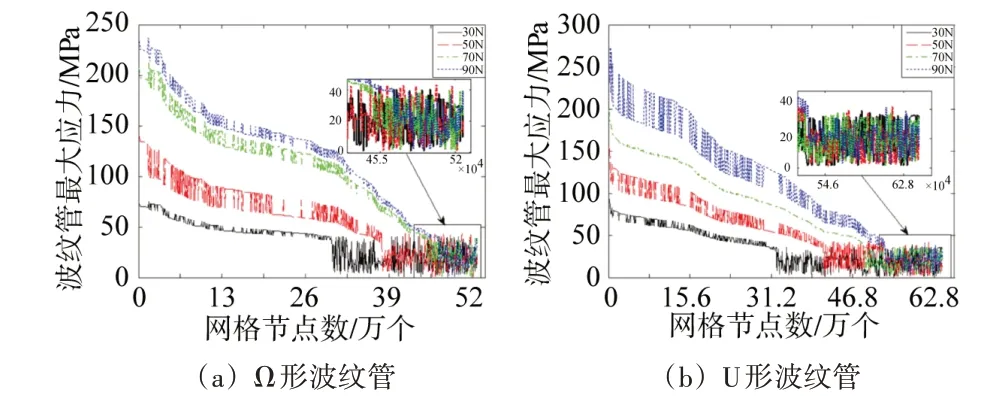
图9 Ω形和U形波纹管最大主应力

图10 Ω形和U形波纹管疲劳失效循环次数

在随机载荷的作用下，Ω 形波纹管和U 形波纹管的最大主应力都随着预应力的增大而增加，最大主应力较大的位置都出现在波峰和波谷附近的结点，其余位置的最大主应力变化趋势较为平稳，集中在50 MPa 以内。Ω形波纹管和U 形波纹管随着预应力的增大，出现疲劳的结点也逐渐增多，当预应力增至70 N 时，出现疲劳结点的数量增加缓慢，两种波纹管在不同预应力下出现疲劳结点的数量如表2所示。

表2 Ω形和U形波纹管不同预应力下出现疲劳的结点数

以预应力30 N 时为例，对比分析两种波纹管的最大主应力和疲劳失效循环次数，为使对比明显，最大主应力和疲劳循环次数在不改变曲线变化趋势的前提下，对数据进行缩减处理，并使两组数据长度相等。Ω 形波纹管最大主应力每隔650 个点取读一次数据，U 形波纹管每隔800 个点取读一次，处理后的数据完整的保留了曲线的变化趋势，如图11 所示；两种波纹管在预应力为30 N 时，出现疲劳失效的点数接近，不用对数据进行处理，如图12 所示。可以看出U 形波纹管波峰和波谷附近最大主应力大于Ω 形波纹管，其余位置的最大主应力相差不明显，U 形波纹管易发生疲劳失效的结点数要比Ω形波纹管的多，因此相同工况下Ω 形波纹管比U 形波纹管的寿命更长。文献[11]分析了Ω形和U形波纹管的应力分布规律，得出与U 形波纹管相比，在同种规格和同种材料下，Ω 形波纹管的耐压能力更强的结论，与本文所得结论一致。

图11 预应力30 N时最大主应力对比

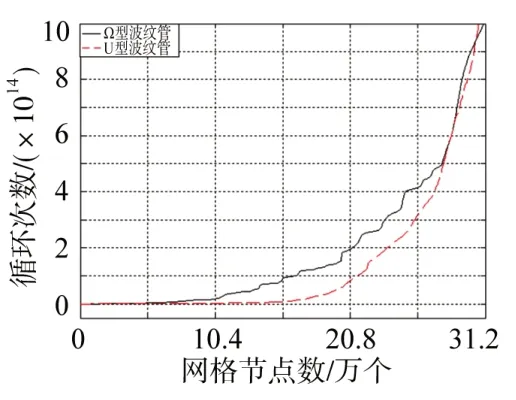
图12 预应力30 N时疲劳失效循环次数对比

3 结束语

本文通过对比分析Ω 形波纹管和U 形波纹管在不同预应力下的等效应力、最大主应力和疲劳循环次数，得到如下结论。

（1）Ω 形和U 形波纹管应力集中的位置都发生在波峰和波谷附近，随着预应力增加，两种波纹管等效应力、应变增加，在相同预应力作用下，U 形波纹管波谷附近等效应力大于Ω 形波纹管，波峰附近等效应力小于Ω 形波纹管。

（2）两种波纹管随着预应力的增大，波峰和波谷处的最大主应力增大，其余位置的最大主应力都集中在50 MPa 以内，随预应力变化量很小；相同预应力下，U形波纹管最大主应力和疲劳损伤都大于Ω形波纹管。

（3）随着预应力的增大两种波纹管出现疲劳的结点数量增多，疲劳损伤增大；相同预应力下，U 形波纹管易发生疲劳失效的结点数要比Ω 形波纹管的多，更容易发生疲劳失效。