基于融合评价指标的k-means聚类算法的地铁车轮踏面磨耗分析

易 佳，陆正刚

（同济大学铁道与城市轨道交通研究院，上海 200092）

0 引言

轮对踏面廓形会随着列车运行里程的增加而不断磨损，当这些磨损超过一定标准限值时，就必须进行镟修，使其恢复到标准外形，从而保证列车的运行安全性。目前主要的镟修方式为等级镟修，由于车轮踏面和轮缘的特殊外形，每恢复1 mm的轮缘厚度，在车轮踏面直径方向上就需要切削掉5 mm 左右[1]，车轮踏面直径方向的镟修量仍然较大。目前，经济镟修方案中主要从两方面进行研究，一个是从经济镟修外形的设计上，另一个是制定合理的经济镟修周期。

在经济镟修外形的设计上，我国众多学者也开展了一定的研究。文献[2-3]提出一种多学科设计优化方法，并验证了该优化廓形能显著减少车轮镟修量。目前对车轮踏面的优化设计大多为单轮对优化设计，优化对象单一，因而所获得的优化镟修外形不具有一定的普适性，在工程实施上还具有一定难度。

面对大量车轮磨耗数据，聚类分析这种对原始数据进行划分的方法成为研究热点。聚类分析即用数学方法研究和处理给定对象分类，是分析学的一种基本方法[4]。聚类分析过程中通常要解决两个问题，即如何划分一个给定的数据集并使得划分结果最优以及确定数据集的最佳聚类数。其中，第一个问题通常由聚类算法来解决，而第二个问题则由聚类有效性指标来评价[5]。k-means 聚类算法作为最典型，也是最常见的一种聚类算法，具有高效、准确的聚类效果，针对车轮踏面外形这类数据的处理具有较好的普适性。聚类有效性指标一般用于判断目标数据集的最佳聚类簇数。目前，已有一些经典的指标，如CH 指 标[6]、COP 指 标[7]、DB 指 标[8]、Dunn 指 标[9]以及I指标[10]等得到广泛应用。

本文基于现有的车轮磨耗数据，从指标间的差异程度出发，分析聚类特征数据对聚类数的影响；基于kmeans 算法，提出融合评价指标确定聚类数及评价聚类效果；选择聚类效果最好的方案对所有待镟修的磨耗踏面开展聚类分析，并对聚类方法进行适应性分析，验证方案的有效性，为车轮经济优化镟修提供参考。

1 地铁车辆轮对踏面磨耗特征分析

以某条线路的地铁为例，列车为6 节编组，共28 列车。本文以该线路地铁2022 年9 月底所有车轮为研究对象，并对车轮踏面外形进行了数据预处理，最终得到1 344个车轮外形数据，按照车轮几何参数的统计数据如图1～3所示。

图1 车轮的轮缘厚度分布情况

图1 所示为所有车轮的轮缘厚度分布情况。由图可知，轮缘厚度大概在3 个范围分布较为集中，分别为7.5、29、31 mm 左右。图2所示为轮缘高度分布情况。图3 所示为qR 值分布情况。由图可知，qR值的变化范围相对集中，轮缘高度大概在3个范围分布较为集中，分别为27.8、28.5、30 mm左右。

图2 车轮的轮缘高度分布情况

图3 车轮的qR值分布情况

目前针对薄轮缘踏面的优化设计研究，基本上是针对列车中某一个车轮踏面进行优化设计。但在实际列车运营中，由于不同车轮会产生多种不同的磨耗踏面，若要同时对每个磨耗踏面进行优化镟修是不切实际的，在工程上没有可操作性。

因此，针对每一列车里不同轮对的踏面磨耗情况及相近特征，采用聚类分析方法，将相似度高的磨耗踏面归为同一类，进行统一的镟修优化分析是比较好的解决方案。

2 聚类分析方法

2.1 聚类特征选择方法

对于聚类指标的选取，可在进行聚类分析之前运用相关性分析，方差计算，结合专业知识对指标进行筛选，尽量采用那些在不同类别之间存在明显差异的指标，剔除那些类间差异不明显的指标；亦可在聚类分析后，利用类间方差分析结果进行指标筛选，剔除不具有显著性差异的指标，使分类结果客观真实[11]。本文综合考虑轮对参数相关性和方差分析选择聚类指标。

对各个轮对参数进行相关性分析，以各轮对参数的方差作为评价数据集的离散程度指标，方差越大，代表该维度的数据区分度越大，定义如式（1）所示。

式中：XiN为各类踏面数据中的N个数据样本；μi为各类踏面数据的均值。

2.2 聚类特征变换方法

在进行聚类分析时，由于聚类指标的量纲差异，可能会掩盖其他变差效度指标作用，因为数量级单位大的指标往往其变化差异也大，相对权重将会增大。因此，未标准化的数据相当于具有不同的权重，可能会对数据的真实结构产生很大影响[13-14]，但出于某种需要，为强调某指标的意义时，也可通过计算加权距离的方法实现[12]。本文选用4种不同的聚类参数处理方法进行研究分析。

（1）Z-Score 标准化。X用X∗=转换，其中μ和σ为原始数据集X的均值和标准差，X∗为经过变换后的数据集。

（2）最值转换法。X用X∗=转换，其中Xmax和Xmin分别表示X指标的最大值和最小值，X∗为经过变换后的数据集。

（3）相对平均值转换法。X用X∗=转换，其中表示X指标的平均值，X∗为经过变换后的数据集。

（4）权重比定义聚类参数

通过一定的权重比，综合考虑轮缘高度h轮缘、dqR值和轮缘厚度d轮缘这3 个轮对参数。首先，采用权重为1∶1∶1的方式，定义聚类参数如式（2）所示。

其次，采用式（3）定义聚类参数。

式中：η1、η2、η3为相应轮对参数的方差值。

方差作为评价数据集的离散程度指标，可代表数据的区分度，采用方差作为权重系数，利于区分不同磨耗情况的轮对踏面。

2.3 k-means聚类算法原理

k-means 算法[15]，即k均值算法，其根据数据对象的一定特征参数，将相似度大的对象聚成同一类，使不同类别间的相似度尽可能小，是一种无监督式学习算法[16]。k-means 算法基本原理[17]：针对一个确定的数据集，可先随机选择k个数据点作为聚类中心，然后计算每个数据样本到各聚类中心的距离，并归类到距离最近的一个聚类中心，成为一类；接着计算各类数据样本的新的聚类中心，当目标函数的变化小于一定限度时，表示聚类中心收敛，否则返回重新调整各类数据样本。k-means算法具体流程如图4所示。

图4 K-means聚类算法流程

k-means 算法需要提前确定好初始聚类数目k及k个初始聚类中心，因此最关键的部分是确定聚类簇数。本文结合“平均轮廓系数”和“密度指标”，提出融合评价指标确定k值，在聚类算法某一数据集聚类划分结束后，亦可通过聚类有效性指标函数计算出的数值来评价聚类划分的好坏[18]。

（1）密度指标

聚类有效性指数SDbw基于的标准（即紧凑性和分离）是聚类的基本标准。它通过对比“类内的紧密性”和“类间的密度”来评估聚类的有效性。计算式如式（4）～（6）所示。

式中：Scat(c)为c个聚类内的平均散布情况，该值越小，说明聚类越紧凑；Dbw(c)为c个聚类之间的平均点数，即聚类间密度，与聚类内的密度有关，该值越小，说明类间分离的越好；d(vi)为第i类的聚类中心vi的密度；d(vj)为第j类的聚类中心vi的密度；d(uij)为第i类和第j类之间的聚类中心uij的密度；‖σ(Ci) ‖为向量σ(Ci)的L2 范数，即与原点的欧氏距离[19]；σ(D)为数据集D，即所有样本的方差向量；‖σ(D) ‖为向量σ(D)的L2 范数。聚类有效性指数SDbw达到最小时的聚类数目k被认为是数据集中存在的聚类数目的最佳值。

（2）平均轮廓系数SC

当密度指标判断效果不显著时，引入另一聚类有效性指标SC，如式（7）所示。

式中：a(i)为某个样本与其所在簇内其他样本的平均距离；b(i)为某个样本与其他簇样本的平均距离；N为样本数量。其中，SC取值范围为[-1，1]，其值越接近1 代表这一类里的数据与其他类的数据差别越大，同一类里的数据相似性越高。

（3）融合评价指标S

该指标能将密度指标与SC相结合，当其中一方变化不明显时，能更清晰、快速地对k值做出准确判断。

由于密度指标取值范围不确定，且其值越小越好，要对其进行转换，具体计算如式（8）所示。

式中：SD为转换后的密度指标值。

结合密度指标和SC值，通过熵权法计算权重得到融合评价指标，具体如式（9）～（10）所示。

式中：S为融合评价指标值；wi为各项指标权重；m为指标个数，这里m=2；dj为计算信息熵冗余度；j为指标个数，取j=2。最后S取值范围为[0，1]，其值越接近1表示聚类效果越好。

3 基于磨耗踏面廓形的聚类分析

3.1 聚类特征选择

表1所示为轮对参数（1 344个数据组）的方差计算结果。图5所示为轮对参数的相关性情况。由图可知，轮缘厚度、等效锥度和qR值三者之间相关性较强，踏面径向磨耗量和轮缘高度之间相关性较强，为降低数据维度，可减少相关性较强的轮对参数。根据表1可知，轮缘高度、轮缘厚度、qR值的方差较大。因而综合相关性和方差分析，最终选取轮缘厚度、轮缘高度以及qR值作为聚类特征参数。

表1 轮对参数方差

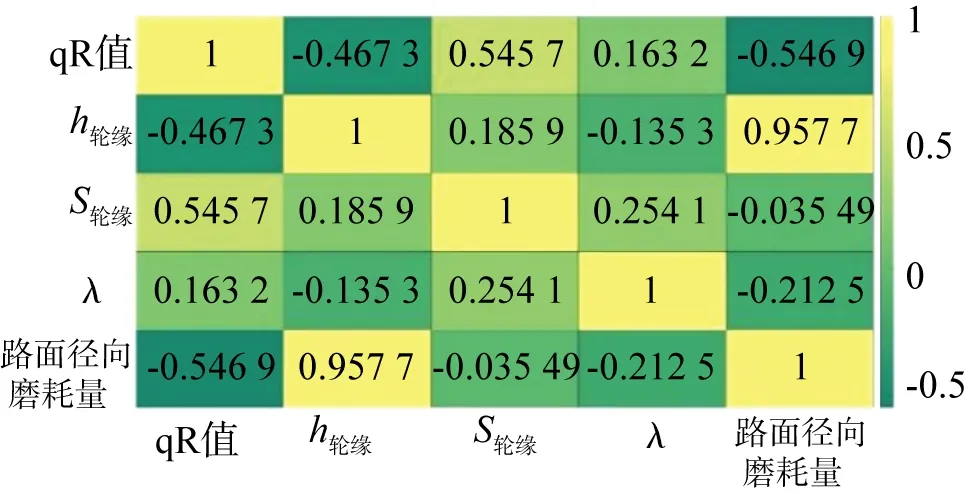
图5 轮对参数相关性

3.2 聚类特征变换影响分析

3.2.1 聚类特征变换方法对聚类参数的影响

将选取的轮缘厚度、轮缘高度以及qR值作为聚类特征参数，并将其经过4 种聚类参数转换方法处理后，计算总平均值、最大（Xmax）最小（Xmin）值及标准差（Sˉ）列于表2。结果表明，有些聚类参数转换方法对上述特征值有极大的压缩作用，可大大减小聚类参数间的离散程度；有些聚类参数转换方法能保留特征值的差异性，可使聚类效果更接近原始数据分类。对于最值转换方法，无论原始数据的聚类参数极差和离散程度多大，该方法均能有效地将最大值和最小值压缩到1和0，从而能大大减小聚类参数的离散程度；对于方差权重转换法通过方差加权区分特征参数在聚类过程中的影响，加强重要特征参数的影响，对簇的形成起积极作用。

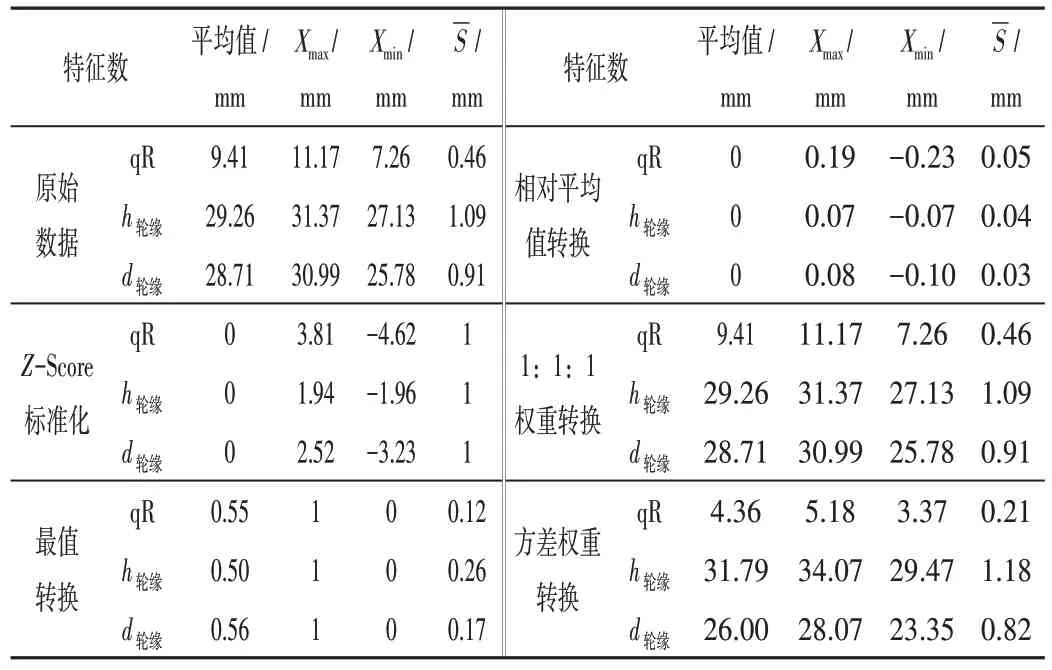
表2 聚类特征变换方法处理后的特征参数统计值

3.2.2 聚类特征变换方法对聚类数的影响

针对不同聚类特征变换方法计算聚类数（k值），比较其差异性。

（1）Z-Score标准化

根据标准化后定义聚类参数Z1，根据聚类参数Z1进行聚类分析，得到如图6 所示的聚类有效性指数（SDbw）和平均轮廓系数（SC）随聚类数（k）的变化曲线。由图可知，当k＜4 时，SDbw下降明显，在k=4 和k=7 时，SC出现峰值，随着SDbw的变小，聚类效果变好。综上，k=7。

图6 标准化后不同类别对应的SDbw指标

（2）最值转换

根据最值转换后定义聚类参数Z1，根据聚类参数Z1进行聚类分析，得到如图7所示的SDbw和SC随k的变化曲线。由图可知，当k＞3 时，SDbw下降明显，在k=4 时SC出现最大值，随着SDbw的变小，聚类效果变好。综上，k=7。

图7 最值转换后不同类别对应的SDbw指标

（3）相对平均值转换

根据相对平均值转换后定义聚类参数Z1，根据聚类参数Z1进行聚类分析，得到如图8所示的SDbw和SC随k的变化曲线。由图可知，当k＜6时，SDbw下降趋势明显，当k=2 时，SC出现最大值，但聚成两类无法很好地展示出车轮的磨耗特征，随着SDbw的变大，聚类效果变差。综上，k=4。

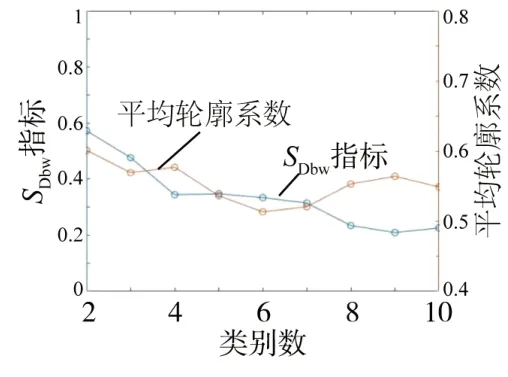
图8 相对平均值转换后不同类别对应的SDbw指标

（4）1∶1∶1权重转换

根据式（2）1∶1∶1 加权后定义聚类参数Z1，根据聚类参数Z1进行聚类分析，得到如图9 所示的SDbw和SC随k的变化曲线。由图可知，当k＜6 时，SDbw下降趋势明显，当k=7 时，SC出现最大值，随着SC的变小，聚类效果变差。综上，k=7。

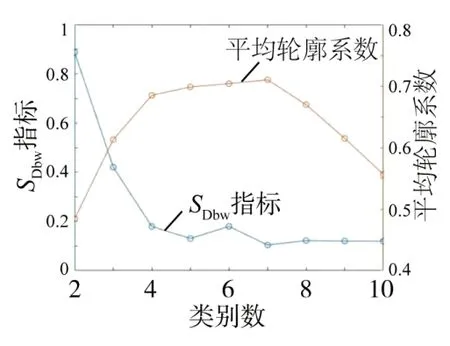
图9 不同类别对应的SDbw指标

（5）方差权重转换

根据式（3）方差加权后定义聚类参数Z1，根据聚类参数Z1进行聚类分析，得到如图10所示的不同类别数计算的SDbw和SC指标。由图可知，当k为5 和6 时，SC值最大，聚类数为5与聚类数为6的SDbw指标相当，聚类数大于6 时，SC下降明显，随着SC的变小，聚类效果变差。综上，k=5。

图10 不同类别对应的SDbw指标

3.3 融合评价指标S下聚类数分析

采用融合评价指标对不同聚类参数转换方法的k值进行选择，选取其值最大时对应的k作为最佳聚类数，并根据指标大小对比聚类效果。如图11 所示，其k值计算结果与图6～10 结果一致，方差权重和1∶1∶1 权重的聚类特征转换方法的综合指标值较高，其中方差权重转换能在原始数据上放大各指标差异性，方差权重最终k=5，1∶1∶1 权重最终k=7，可知有效区分各指标的重要性，在原始聚类参数上进行方差加权能提高聚类效果，保证信息的完整性。

图11 不同聚类参数转换方法的综合指标值随k变化

因此，最后采用融合评价指标确定k值，采用方差权重转换法对聚类特征参数（h轮缘，d轮缘，qR 值）进行处理后，基于k-means算法进行聚类分析。

3.4 聚类分析结果

针对该线路地铁2022年9月底的1 344个车轮外形数据，选用方差权重转换后的轮缘厚度、轮缘高度、qR 值进行聚类分析，进一步得到车轮踏面的5 种典型磨耗廓形。图12 所示为所有1 344 个车轮聚类分析后按类描述的踏面外形叠加图，对应分成5 类，划分在同一类的踏面外形相似度较高，整体外形较接近。同时，基于聚类结果，针对每一类磨耗踏面，采用均值法获得该类踏面的典型磨耗踏面外形，具体车轮外形如图12所示。由图可知，5 类典型磨耗踏面的区别主要在轮缘和踏面磨耗处。图13 所示为典型磨耗踏面的磨耗量情况，其中第2类和第3类磨耗量较少。图14所示为聚类中心分布情况。由图可知，5 个聚类中心有明显区别，距离相隔较远，典型廓形具体的轮对参数如表3所示。

表3 五类典型磨耗踏面的轮对参数

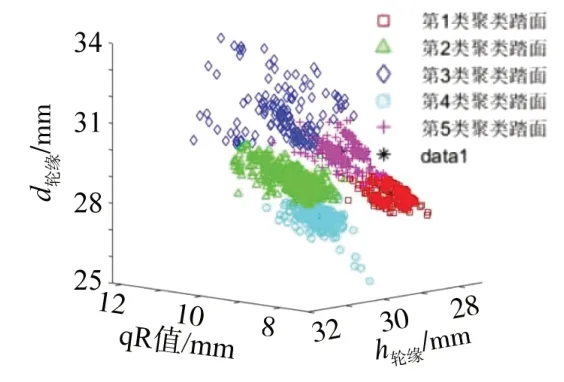
图12 车轮踏面聚类效果

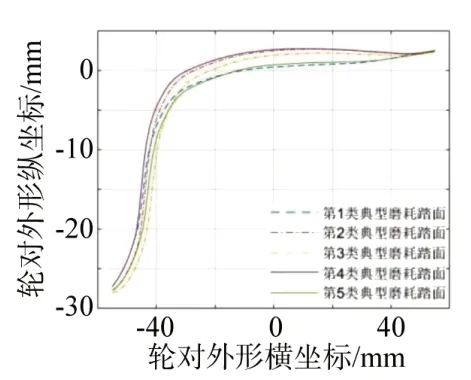
图13 5个典型磨耗踏面外形

图14 典型磨耗踏面外形磨耗量

图15 聚类中心分布

3.5 聚类分析方法适应性检验

为验证该聚类方法的适应性，应选择与原始数据日期较为接近的另外两组数据进一步分析。这里选取该线路2022 年9 月初及2022 年7 月初的两组车轮廓形数据，基于融合评价指标的k-means聚类算法进行k值分析。如图16～17 所示，方差权重和1∶1∶1 权重的聚类特征转换方法的综合指标值较高，针对9 月初数据，方差权重最终k=5，1∶1∶1 权重最终k=5，针对7 月初数据，方差权重最终k=5，1∶1∶1 权重最终k=6。对比9 月底的聚类数k变化，最终选用方差权重方法得到的综合指标值最高，k值均为5，由此验证了方差加权法对聚类参数进行处理的有效性。

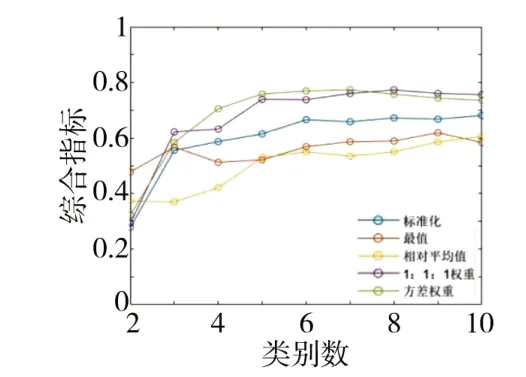
图16 不同聚类参数转换方法的综合指标值随k变化（9月初）

图17 不同聚类参数转换方法的综合指标值随k变化（7月初）

4 结束语

本文对某地铁公司同一线路的1 344个轮对的车轮踏面磨耗情况进行分析，基于聚类分析方法研究分析聚类效果的影响因素，并对地铁车轮踏面进行聚类分析研究，主要结论如下：

（1）影响聚类分析方法应用效果的因素主要包括聚类指标因素、数据处理。在进行聚类分析之前，必须充分做好前期工作，尽量考虑变量之间的相关性，尽量减少不良影响的作用。

（2）提出一种基于融合评价指标的k-means 聚类算法，以带权重的轮缘高度h轮缘、轮缘综合值qR和轮缘厚度d轮缘作为描述踏面特征的聚类参数，将密度指标与平均轮廓系数SC结合得到融合评价指标S确定聚类数K值，同时使用各个轮对参数（h轮缘、qR、d轮缘）的方差作为权重，每一类车轮磨耗踏面外形的聚类结果具有较高的准确性。

（3）基于聚类结果，针对每一类磨耗踏面，采用均值法获得该类踏面的典型磨外形，并对聚类方案的适应性进一步分析，验证了方案的普适性。

进一步地，将针对每一类典型磨耗廓形进行镟修模板优化，制定合理的经济优化镟修策略，为实现地铁车轮踏面优化经济镟修的工程应用奠定基础。