基于动态簇粒子群优化的无人机集群路径规划方法

王龙宝，栾茵琪，徐亮，曾昕，张帅，徐淑芳*

基于动态簇粒子群优化的无人机集群路径规划方法

王龙宝1，2，栾茵琪1，徐亮3，曾昕3，张帅4，徐淑芳1，2*

（1.河海大学 计算机与信息学院，南京 211000； 2.水利部水利大数据技术重点实验室（河海大学），南京 211000； 3.长江生态环保集团有限公司，武汉 430014； 4.中国电建集团昆明勘测设计研究院有限公司，昆明 650051）（ ∗ 通信作者电子邮箱xushufang@hhu.edu.cn）

路径规划对于无人机（UAV）集群的任务执行十分重要，而且高维场景中的计算通常很复杂。群体智能为解决该问题提供了较好的解决思路。粒子群优化（PSO）算法具有参数少、收敛速度快、操作简单等优点，尤其适用于路径规划问题，但它在应用时存在全局搜索能力差、容易陷入局部最优的问题。为了解决上述问题以提升无人机集群路径规划的效果，提出了动态簇粒子群优化（DCPSO）算法。首先，利用人工势场法和滚动时域控制原理建模UAV集群路径规划问题的任务场景；其次，引入Tent混沌映射和动态簇机制进一步提升全局搜索能力和搜索精度；最后，使用DCPSO算法优化模型的目标函数，以获得UAV集群的每个轨迹点的选择。在单峰/多峰、低维/高维不同组合的10种基准测试函数下的仿真实验结果表明，与PSO、鸽子启发优化（PIO）、麻雀搜索算法（SSA）和混沌扰动鸽群优化（CDPIO）算法相比，DCPSO算法具有更好的计算最优值、均值和方差，搜索精度更佳，稳定性更强。此外，UAV集群路径规划应用实例仿真结果也验证了DCPSO算法的性能与效果。

粒子群优化；动态簇机制；无人机集群；路径规划；滚动时域控制

0 引言

无人机（Unmanned Aerial Vehicle， UAV）路径规划是无人机各项任务中涉及的关键问题。无人机在到达目标点执行特定任务之前，必须规划从起点到下一个任务点的合理路径，并成功避开障碍物；但实际场景中的任务一般非常复杂，单架无人机存在效率低、响应慢、有时无法完成复杂任务的问题。无人机集群可以解决单架无人机效率低等问题，通过集群内的相互感知和信息交换，无人机集群可以在敌对的复杂环境中以较低的成本完成复杂的任务，这就要求无人机集群能够安全高效地完成路径规划工作。

近年来，无人机集群路径规划主要有两个研究方向：一种是经典路径规划算法，如梯度下降法［1］和图论法［2］；另一种是群体智能优化算法，如麻雀搜索算法（Sparrow Search Algorithm， SSA）［3］和鸽子启发优化（Pigeon-Inspired Optimization， PIO）［4］。但经典算法通常伴随着各种各样的问题，例如，梯度下降法需要大量的迭代计算，不能保证优化效果。群体智能优化算法是一种模仿生物集群行为产生的算法，擅长处理复杂的多约束优化问题［5］。

粒子群优化（Particle Swarm Optimization， PSO）［6］是经典的群体智能优化算法，具有参数少、计算简单、收敛快等优点，适合解决无人机集群复杂路径规划问题；但PSO本身也存在精度低、易陷入局部最优的问题。文献［7］中提出了一种结合PSO的自适应差分进化算法，它的核心思想是根据粒子偏离全局最优解的程度分配不同的搜索模式，并将所提出的算法应用于无人机集群路径规划中，取得了良好的效果；文献［8］中利用时变自适应惯性权重的思想，提出了一种具有较高种群多样性的改进PSO算法，并成功应用于无人机集群路径规划；文献［9］中将遗传算法和PSO有机结合，成功应用于无人机集群路径规划。

由于PSO容易陷入局部最优，所以改进PSO意义巨大。文献［10］中在局部最优解附近添加混沌扰动算子，使它具有突跳能力，进而提高全局搜索能力；文献［11］中使用Tent混沌映射进行混沌填充，增强初始化阶段的种群多样性，有利于种群在早期演化阶段遍历整个可行解域。混沌映射通常被用来解决在初始化种群时快速陷入局部最优的问题，本文利用Tent混沌映射具有的随机性和遍历性，改善PSO在初始化种群时快速陷入局部最优的问题；然而，种群在移动过程中仍会出现容易陷入局部最优的问题，因此，本文引入了动态簇机制。

本文针对全局搜索能力弱的共性问题进行了改进，针对它在高维复杂环境中路径规划的应用，提出了动态簇PSO（Dynamic Cluster Particle Swarm Optimization， DCPSO）算法，采用Tent混沌映射和动态簇机制进行改进。通过实验充分验证了DCPSO在复杂任务场景下无人机集群路径规划中的有效性。本文还揭示了生物群体智能应用于无人机集群路径规划的一般规律，为生物群体智能优化算法和无人机集群智能提供理论依据和应用参考。

1 相关工作

1.1　问题描述

假设无人机集群从基地出发，飞向任务地点，协同执行特定任务。要求无人机集群合理规划飞行路径，到达任务位置执行后续任务，同时避开途中障碍物。假设一组具有相同配置的携带传感器检测设备的无人机集群，且规定每个无人机可以相互通信。在巡航任务期间，无人机集群通常在规定的高度飞行且高度不变。任务区设置为矩形区域，无人机集群从起飞区域出发，按照规划路径避开多个障碍物到达任务点。为了在路径规划中合理地描述无人机集群的状态，需要设计一个高效的模型构建任务场景。

本文使用人工势场的方法构建任务场景。人工势场法是由Khatib［12］提出的一种虚拟力方法，常用于机器人路径规划。该方法将环境抽象地模拟为一个力场，通过作用在物体上的重力和排斥力实现路径规划。通常，无人机朝向的目标点会对物体产生重力，而需要避开的障碍物会对物体产生排斥力，从而使物体可以避开环境中的障碍物到达目标点，最终实现合理的路径规划。

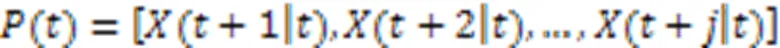
本文将无人机集群路径规划问题转化为多约束优化问题。以无人机为例，使用式（2）优化上述问题：

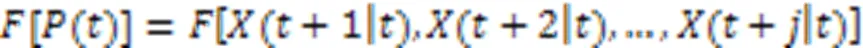
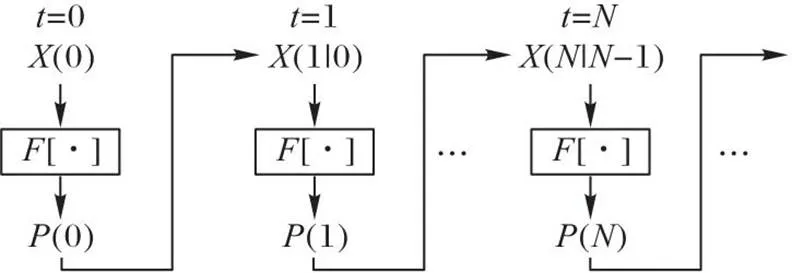
图1　无人机集群路径规划模型的结构

1.2　无人机集群相应规则

为了便于研究，本文简化了无人机集群运动规则和环境模型。无人机集群的高度在仿真模型中是固定的，因为它在实际巡航任务中通常变化很小，从而将实际问题转化为二维场景，飞行环境也转化为二维平面；此外，将无人机集群视为一组粒子并限制飞行过程中的最大偏航角。对于无人机集群飞行环境进行离散网格处理，其中每个网格中心都有代表整个网格的信息值。

1.2.1人工势场法

根据问题描述，可知任务场景中只有一个目标点，所以在终点给出一个低势能，为无人机提供更大的牵引力。将任务场景设置为矩形区域，并构建笛卡尔坐标系。使用式（3）在目标点处布置了一个山谷型势场［3］。

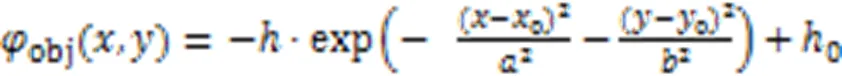
对于任务场景中的障碍物，使用式（4）构建山势场：

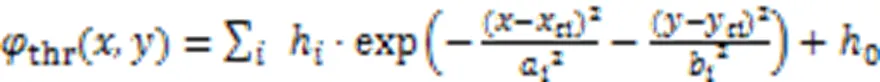
取两个局部势场中较高的两个值相加作为总势场，得到无人机集群路径规划的人工势场，如式（5）所示：

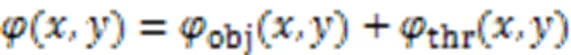
1.2.2滚动时域控制

使用滚动时域控制策略对无人机集群路径规划进行离散处理。以无人机为例，无人机每个时刻都覆盖一个滚动时域窗口，随着时间推移向前移动［13］。由于无人机集群路径规划的长度是不确定的，且在实际场景中通常很长，如果将整个无人机集群的路径作为优化问题的输出，要优化的函数在高维上会变得非常复杂，因此，本文采用滚动时域控制策略解决这个问题。

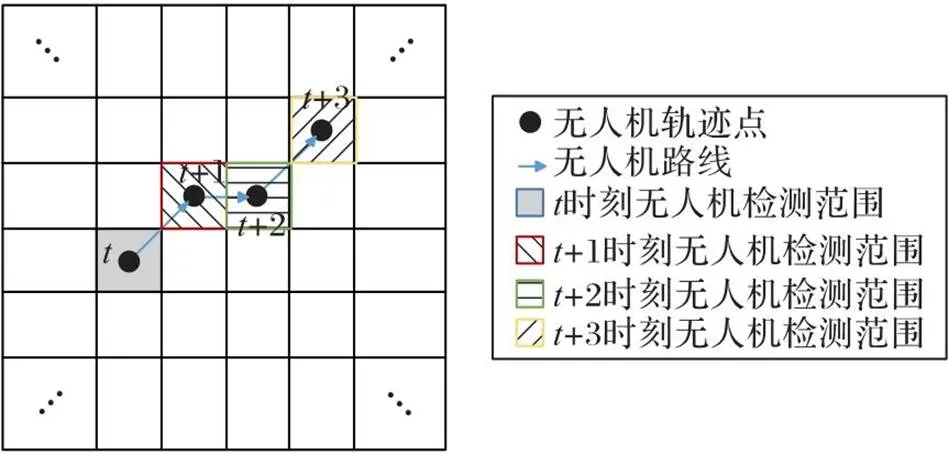
图2　滚动时域控制策略示意图

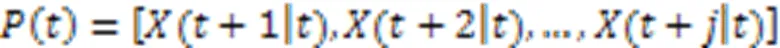
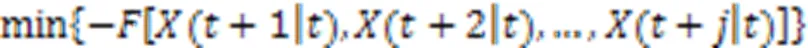
2 算法提出

2.1　算法基础

2.1.1PSO算法

PSO是一种受鸟类觅食机制启发，基于一种速度和位置搜索模型的群体智能优化算法。这种算法是一种并行算法，具有实现简单、精度高、收敛快等优点，对于解决实际问题存在重要意义。与大多数群体智能优化算法一样，整个种群是问题的输入和待优化的输出，每一个个体都是一个候选解。

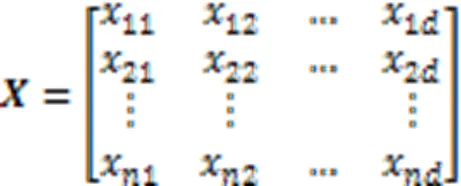
粒子群算法的迭代公式如式（9）所示：

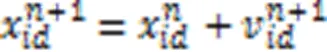
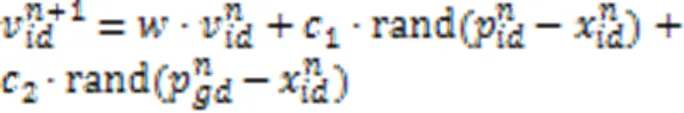
式（10）中的社会机制为算法提供了牵引力，但也制约了算法的全局搜索能力。

2.1.2Tent混沌映射

混沌映射是非线性系统中一种特别非周期性的现象，它普遍存在，具有随机性、遍历性和规律性等特点。使用混沌映射初始化种群，可以有效增加初始种群的多样性，提高初始解的质量和全局优化能力，有效避免陷入局部最优的情况。Tent映射［14］是典型的混沌系统，因它的函数图像类似帐篷又被称为帐篷映射，呈现比较均匀的分布密度，在遍历性、均匀性和迭代速度方面具有相当的优势。迭代更新公式如式（11）所示：

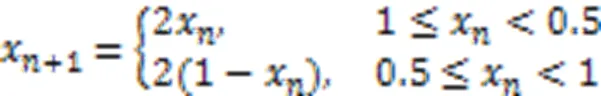
2.2　DCPSO算法

2.2.1动态簇机制

从式（9）（10）可以看出，标准PSO的迭代更新过于依赖社会部分，一旦记录下的整个种群的最优位置趋向局部最优，整个粒子群就会被牵引，进而陷入局部最优。为此，本文改进了这种机制，并生成了一种新的动态簇机制。实验结果表示，粒子群更趋于在最优位置点附近聚集。本文在PSO中引入了动态簇机制，形成一种新的DCPSO算法，以减少粒子之间不必要的通信并扩展全局搜索能力。动态簇机制是一种从自身机制角度提高PSO性能的自适应策略。随着粒子群的不断迭代和更新，算法根据密度对粒子群进行动态分类。与静态簇相比，动态簇机制可能具有更高的复杂度，但相应地，算法性能的整体增益也更大。

动态簇机制［15］有4个过程：选择簇头、聚类、迭代计算和合并以准备下一次聚类。首先，选择每个时刻最密集位置的个体作为第一个簇的簇头1；其次，种群中距离簇头1最近的一半个体被包含在簇1中，其余的个体全部被包含在簇2中，两个簇共享簇内的资源并在簇之间没有交互的情况下进行迭代；最后，合并两个簇，为下一次循环做准备。

如图3（a）所示，由于社会机制的存在，粒子群中的个体会受群体中处于最佳位置的个体的牵引。例如，粒子0被粒子1拖向局部最优1，算法很可能陷入局部最优。如图3（b）所示，通过添加连接机制，这种情况得到改善。根据粒子群的运动机制，可以判断最密集位置的粒子接近的某个最优值；因此，将最密集位置的一半粒子群作为簇1，其余的作为簇2进行不连续迭代。通过这种方式，簇1跟随最优粒子1到局部最优1，簇2跟随最优粒子0到全局最优0。一次迭代后，将簇合并，依此类推，最终整个种群将被引导至全局最优。这样既可以保留簇1原有的PSO趋势，又可以获得由簇2提供的全局搜索能力。

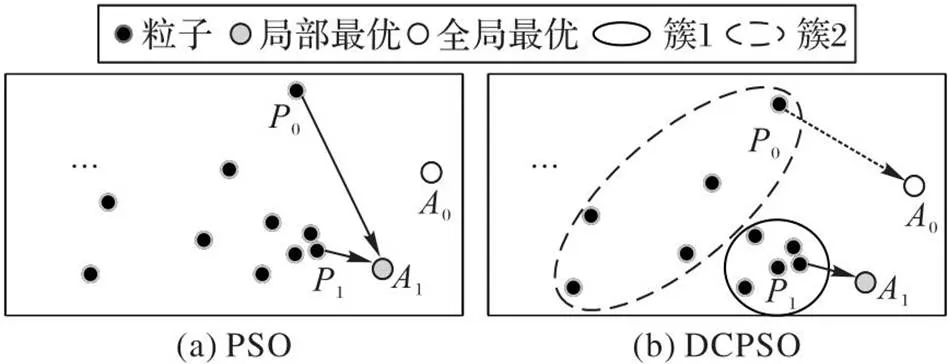
图3　PSO和DCPSO算法的粒子运动对比

2.2.2DCPSO算法

针对PSO在求解复杂高维问题时存在的搜索精度低、易陷入局部最优、鲁棒性差等缺点，DCPSO算法首先使用Tent混沌映射初始化种群，以提高初始种群的多样性；其次，在整个算法过程中采用动态簇机制，进一步提高算法的全局搜索能力和搜索精度。

具体实现步骤如算法1所示。

算法1 DCPSO框架。

输入 最大迭代次数，迭代次数，粒子群大小；

输出 最优解位置，最优适应度值。

1） 根据式（7）和式（11）初始化具有个粒子的粒子群

2） 根据不同需求设计目标函数

3） for= 0 to

4） 使用动态簇机制将粒子群分为簇1和簇2

5） 分别通过PSO更新簇1和簇2

6） 将两个簇合并成一个完整的粒子群

7） 得到当前全局最优值

8） 如果全局最优值优于先前全局最优值，更新全局最优值

9）=+ 1

10） end for

11） return，

2.3　路径规划

在上述建模过程中利用人工势场法和滚动时域控制这两个优化策略可以得到待优化的目标函数，将无人机集群路径规划的问题转化为求解目标函数最优解的问题。根据DCPSO算法构建相应的求解思路并给出算法优化过程，从而实现三维空间的无人机集群路径规划，具体流程如图4所示，详细过程如算法2所示。

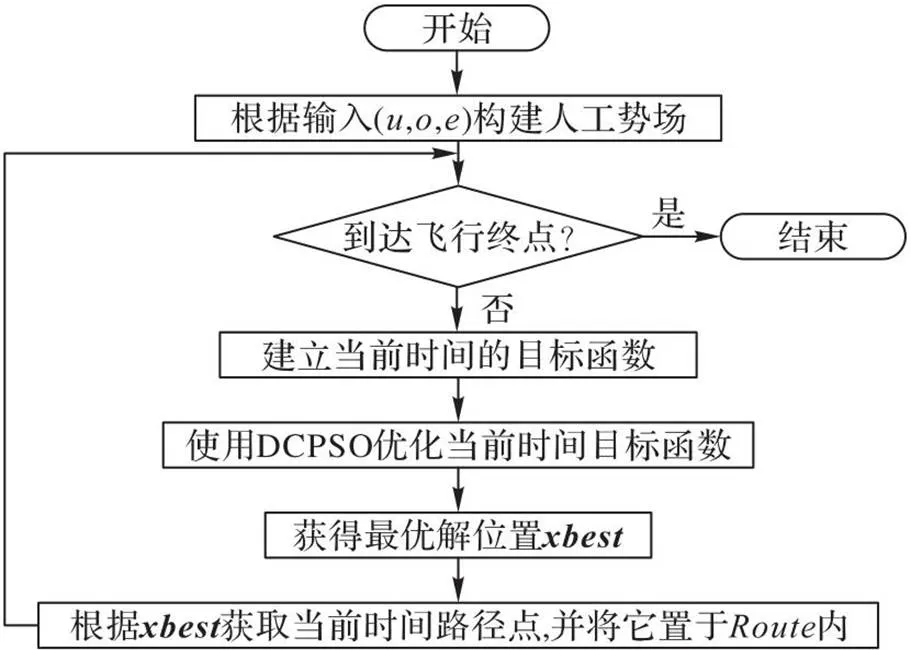
图4　基于DCPSO的无人机集群路径规划流程

算法2 基于DCPSO的无人机集群路径规划步骤。

输入 无人机集群起飞点，障碍物坐标，飞行终点；

输出 无人机集群飞行路径。

1） 根据输入，和构建人工势场

2） While 飞行轨迹不包含

3） 使用式（6）建立当前时间的目标函数

4） 使用DCPSO优化当前时间目标函数，获得最优解位置

5） 根据获取当前时间路径点，并将它置于内

6） end while

7） return

3 仿真实验与结果分析

3.1　仿真环境及参数

3.1.1基准函数

本文使用了单峰低维、单峰高维、多峰低维和多峰高维（http：//www.sfu.ca/～ssurjano/optimization.html）这4种类型的测试函数测试算法的性能。此外，为了避免单次优化的偏差，仿真实验采用了蒙特卡罗模拟方法。每个测试函数运行30次，得到最优值、平均值、标准差和平均时间，最后与标准PSO［6］、鸽子启发优化（PIO）［4］、麻雀搜索算法（SSA）［3］和混沌扰动鸽群优化（Chaotic Disturbance Pigeon-inspired Optimization， CDPIO）算法［16］进行比较。

3.1.2算法参数

PSO、PSO、SSA和DCPSO算法的参数设置如表1所示。

表1PSO、PIO、SSA和DCPSO算法的参数

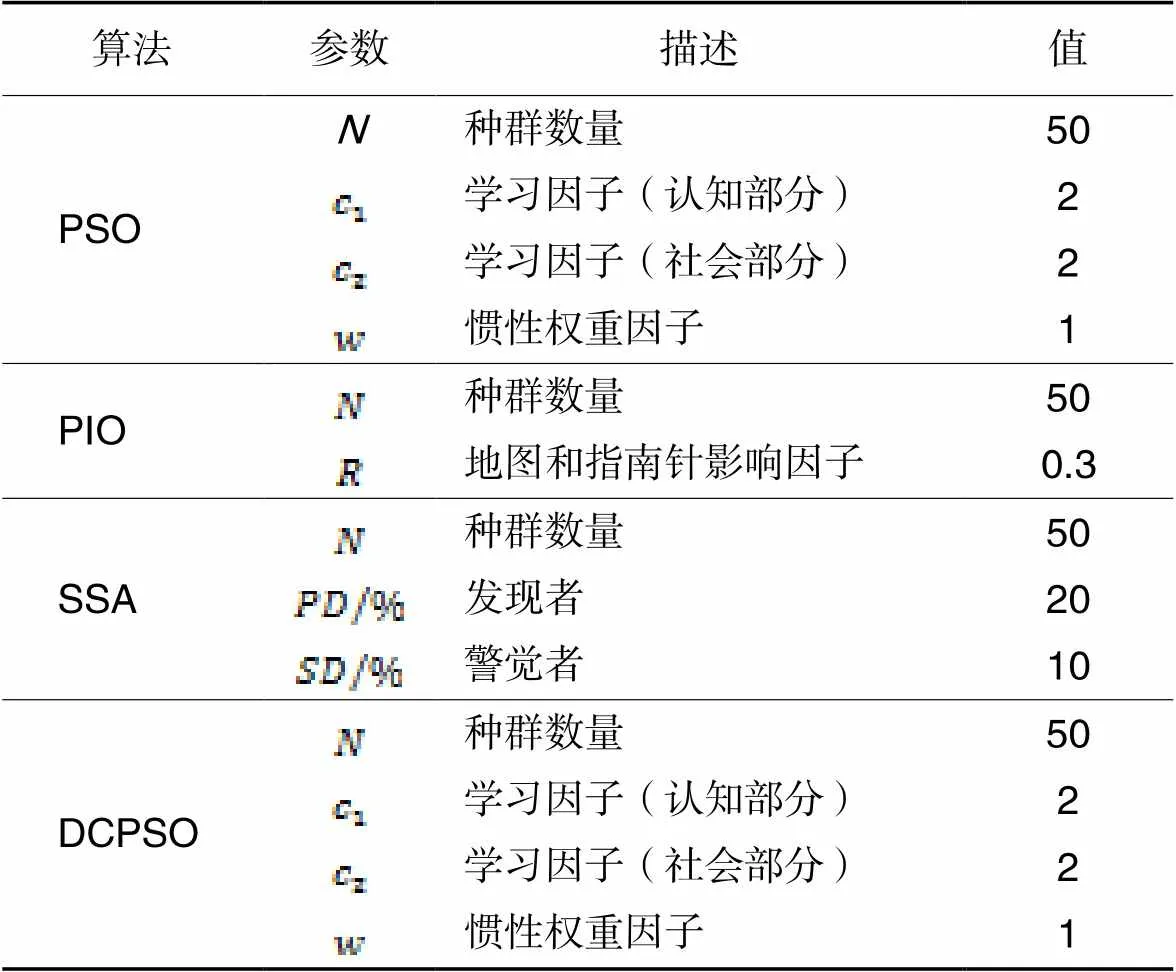
Tab.1　Parameters for PSO， PIO， SSA and DCPSO algorithms

在相同测试函数的条件下，优化结果的最优值可以衡量优化精度；平均值和标准差可以衡量算法的稳定性和鲁棒性，平均耗时则可以反映算法的收敛速度。

实验环境：2.30 GHz Intel I5处理器和4 GB内存；Python 3.8.0。

3.2　实验分析

在DCPSO算法的基础上，本文进一步考虑了算法对不同类型函数的优化能力。

单峰低维测试函数只有一个全局最优且维数较低，可以测试算法在简单情况下的局部搜索能力和搜索精度。单峰高维测试函数只有一个全局最优但维数高，可以测试算法在较复杂情况下的局部搜索能力和搜索精度；多峰低维测试函数具有多个全局最优但维数较低，可以测试算法在比较复杂的情况下的全局搜索能力；多峰高维测试函数具有多个全局最优且维数高，可以测试算法在较复杂的情况下的局部和全局搜索能力。

PSO、PIO、SSAhe DCPSO算法在4种类型的测试函数上经过30次独立实验，实验结果与CDPIO算法实验结果如表2～5所示。

表2单峰低维函数的测试结果

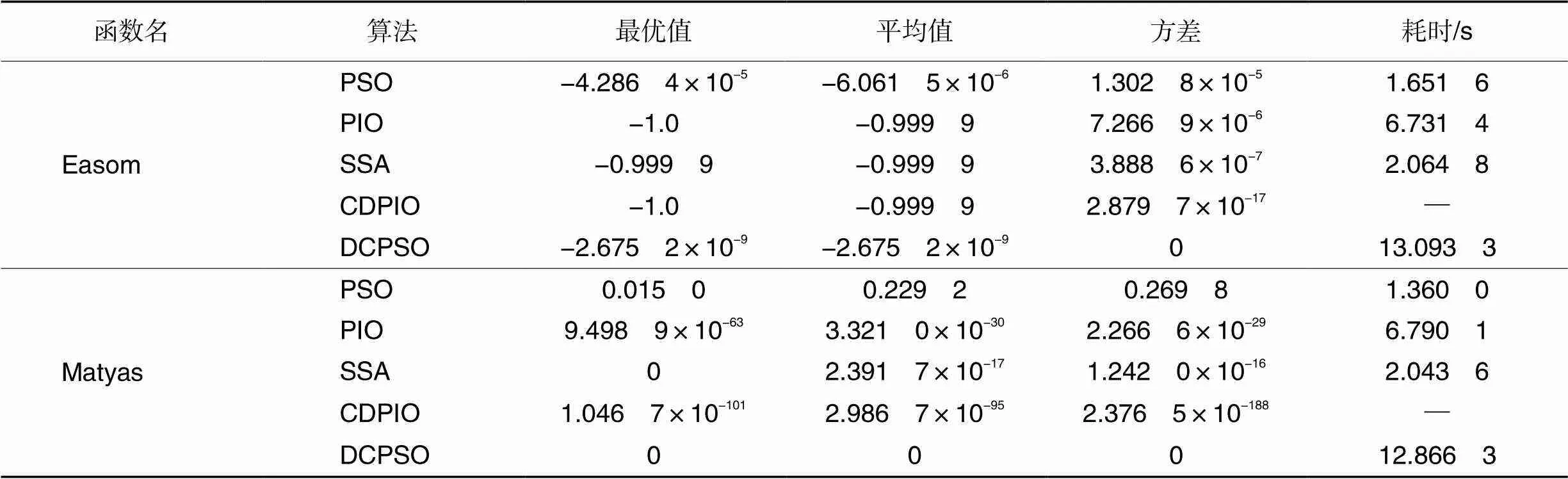
Tab.2　Test results of unimodal low-dimensional functions

表3单峰高维函数的测试结果

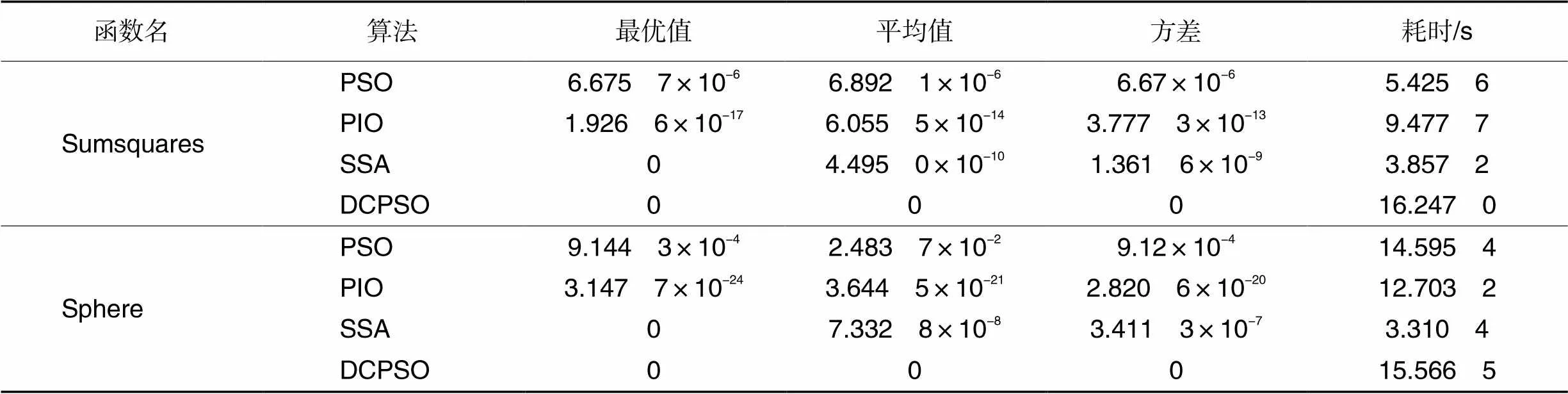
Tab.3　Test results of unimodal high-dimensional functions

表2中，DCPSO算法无法找到Easom函数的全局最优解，但对Matyas函数的优化精度较高，且对Easom函数和Matyas函数都具有较高的鲁棒性，它的优化耗时稍长于其他对比算法。DCPSO算法在优化单峰低维测试函数时是不稳定的，有时DCPSO可以准确快速地找到全局最优解，在搜索精度和稳定性上具有相当优势，有时性能比其他对比算法差。

表3中，DCPSO可以为Sumsquares函数和Sphere函数找到全局最优值，与PSO和PIO相比表现优秀；并且DCPSO得到的平均值和标准偏差最小，标准偏差为0，这意味着DCPSO在稳定性和鲁棒性方面表现优秀。DCPSO算法在优化单峰高维测试函数时能够准确找到全局最优解，在搜索精度和稳定性方面表现优秀。

表4中，DCPSO算法可以找到4个多峰低维测试函数的全局最优值。特别地，与PSO相比，DCPSO具有较大的优势。DCPSO与CDPIO算法得到的平均值和标准偏差最小，标准偏差为0，这意味着DCPSO与CDPIO算法在稳定性和鲁棒性方面优于其他对比算法。

表5中，DCPSO算法可以准确地找到Rastrigin函数的全局最优值，但是4种算法都不能找到Ackley函数的全局最优值。其中，DCPSO和SSA具有最高的搜索精度，并且DCPSO得到的平均值和标准偏差最小，标准偏差为0，这意味着DCPSO在稳定性和鲁棒性方面具有绝对优势。DCPSO的缺点在处理复杂函数时并不明显，因为所有算法都需要较长时间。DCPSO算法在处理多峰高维复函数时，在搜索精度和稳定性方面表现优秀。

表4多峰低维函数的测试结果

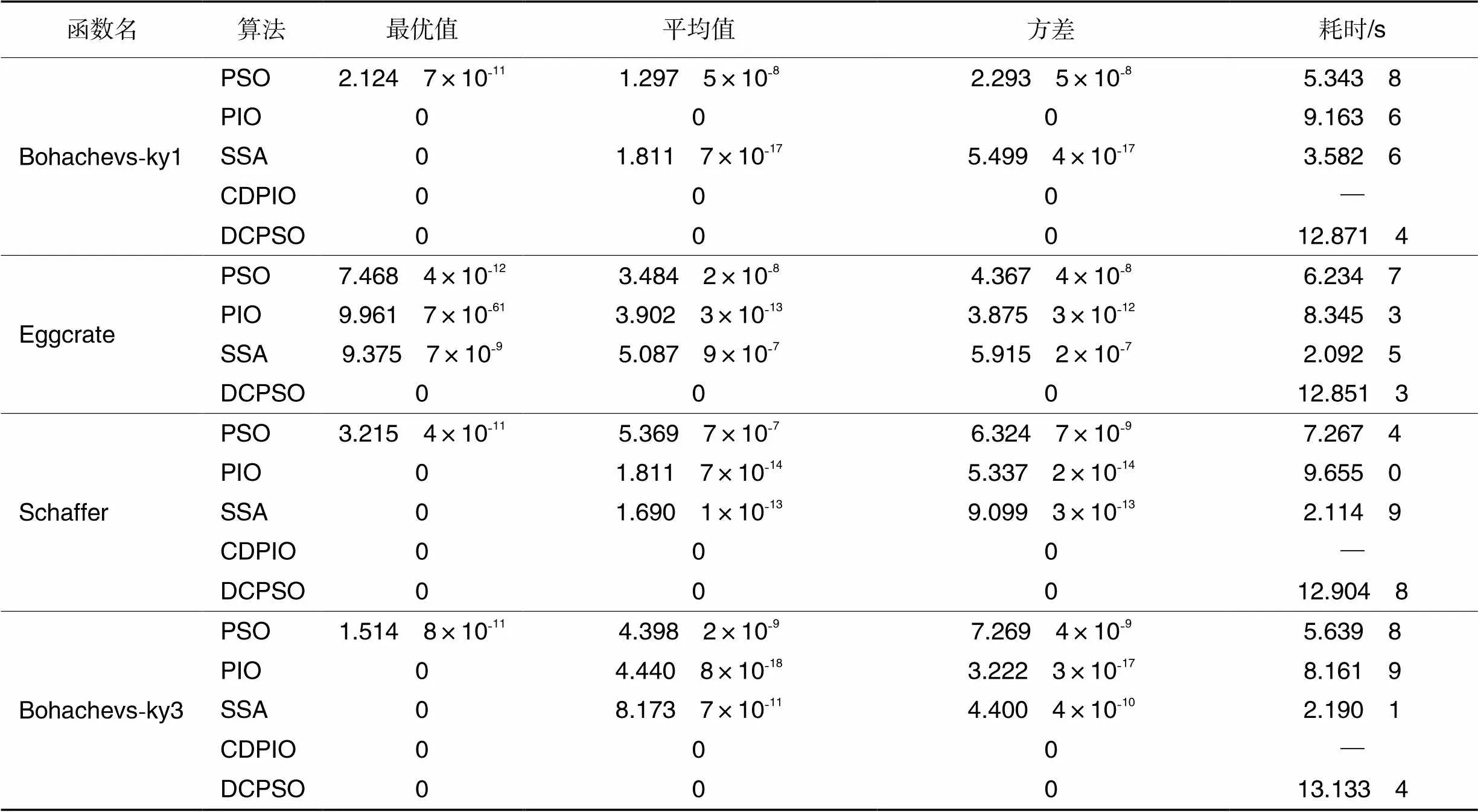
Tab.4　Test results of multimodal low-dimensional functions

表5多峰高维函数的测试结果

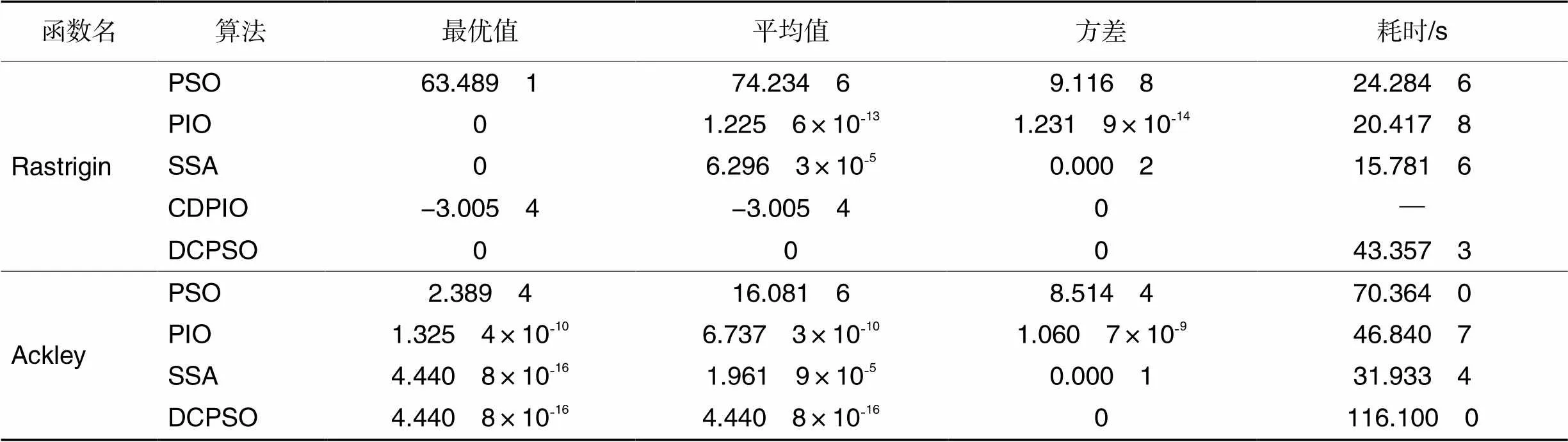
Tab.5　Test results of multimodal high-dimensional functions

综上所述，除处理简单的单峰低维函数情况外，与PSO、PIO、SSA和CDPIO算法相比，DCPSO算法具有高搜索精度和稳定性，但在计算耗时方面有所牺牲，如在优化Rastrigin时，DCPSO算法相较于PSO算法耗时增加了约19 s，但总体而言属于同一数量级，可以借助高性能服务器端弥补耗时问题。对于全域路径规划，DCPSO算法具有相当的优势和竞争力。

4 在无人机集群路径规划中的应用

上一章给出了DCPSO与PSO、PIO、SSA、CDPIO算法对比结果，结果表明DCPSO在搜索精度和稳定性方面优于其他四类算法。基于此，在无人机集群路径规划任务中优选DCPSO进行应用并仿真展示其效果。

4.1　实验参数设置

相关仿真实验参数在表6中列出。仿真实验场景如图5、6所示。图5中，无人机起点、终点和障碍物分别用不同深浅色圆圈标注。图6（a）中，三维图中的轴数值大小表示电位场强度的高低，数值越大，电位场强度越高，图6（b）中，二维图中与原点的距离表示电位场强度的高低，即距离原点近表示电位场强度高，距离原点远则表示电位场强度低。

表6实验参数设置

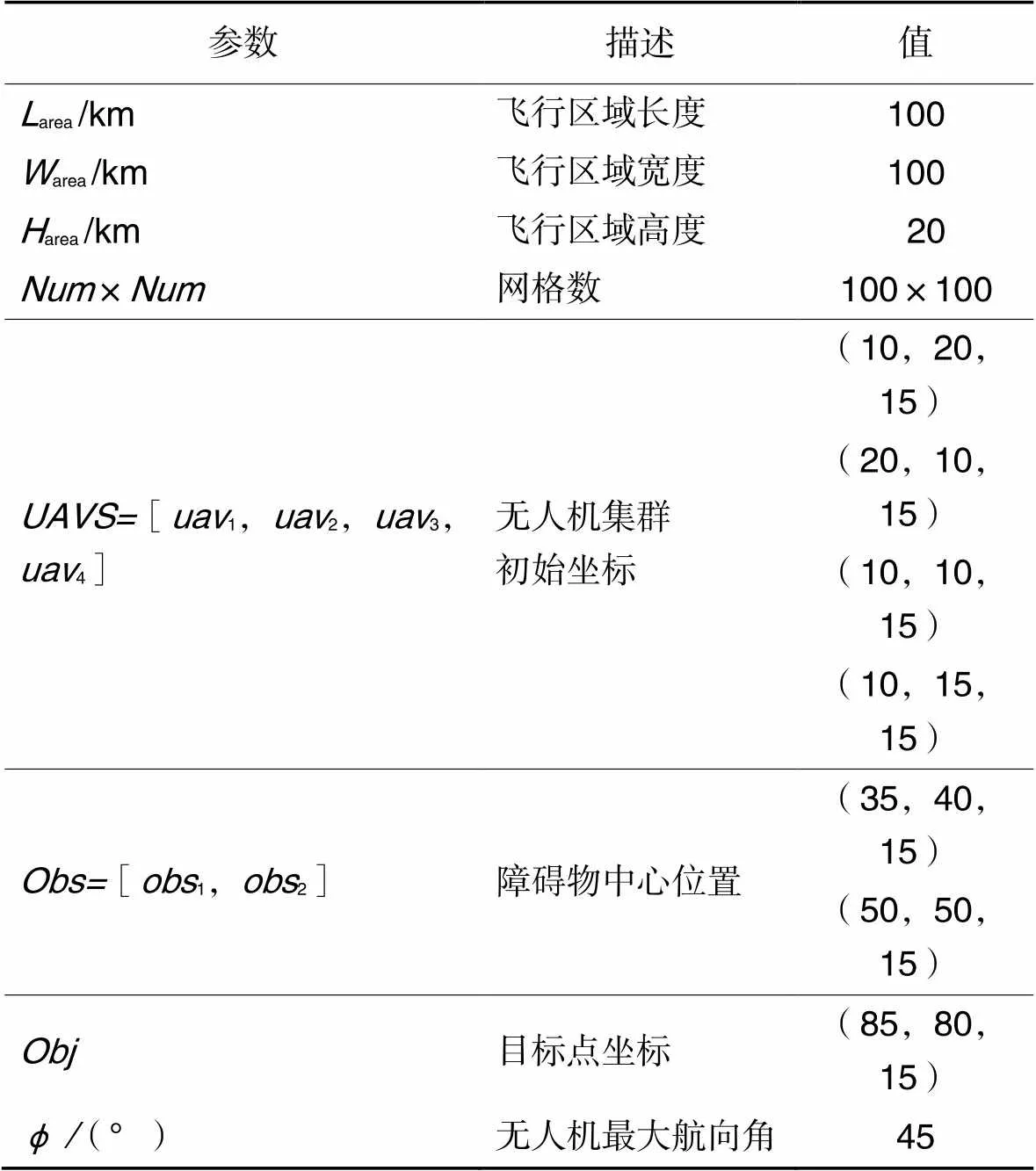
Tab.6　Experimental parameter setting

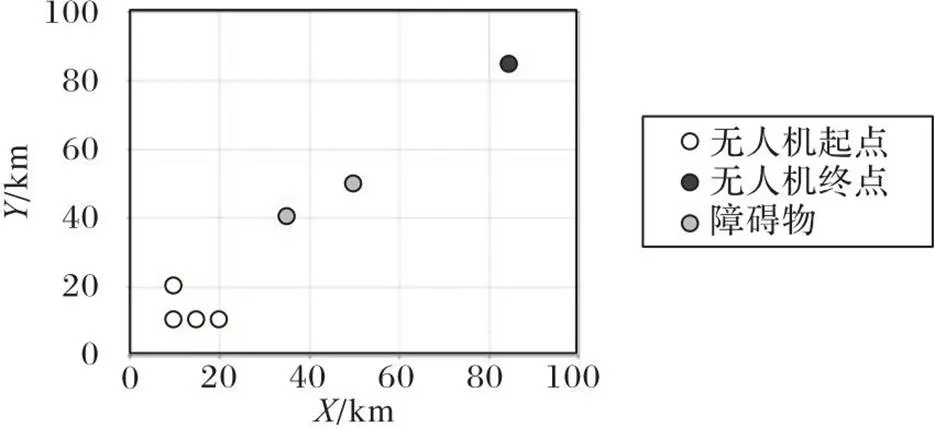
图5　无人机集群、障碍物和轨迹终点分布图

4.2　实验分析

本文在具有挑战性的环境中进行了一系列实验，以验证所提出的DCPSO算法在3D环境下的无人机集群路径规划应用中的性能。首先利用人工势场法对任务场景进行建模，然后利用滚动时域控制策略不断更新下一个最优路径点，最终得到最优飞行路径。实验中采用蒙特卡罗方法独立使用DCPSO算法运行30次，获得轨迹的平均值和标准偏差，进一步验证DCPSO算法的稳定性和有效性。

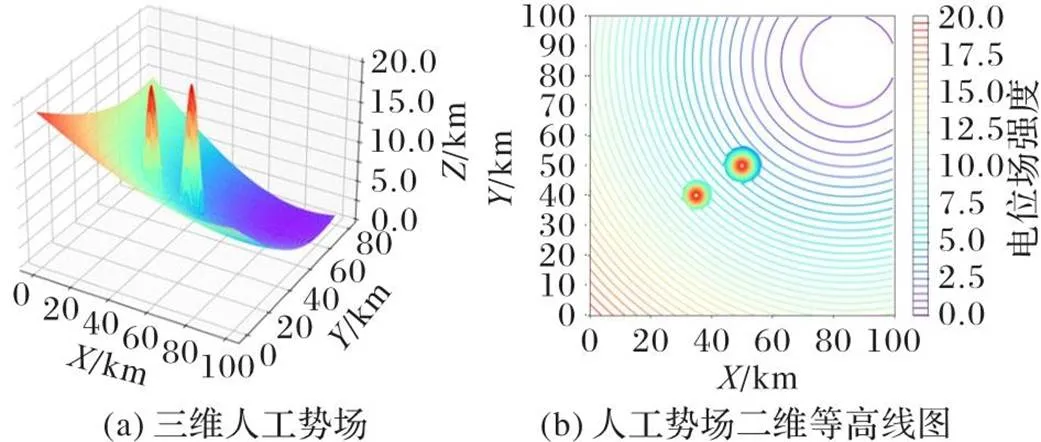
图6　人工势场图

4.2.1可行性

使用DCPSO算法优化无人机集群路径规划过程，图7显示了一项模拟实验的结果。

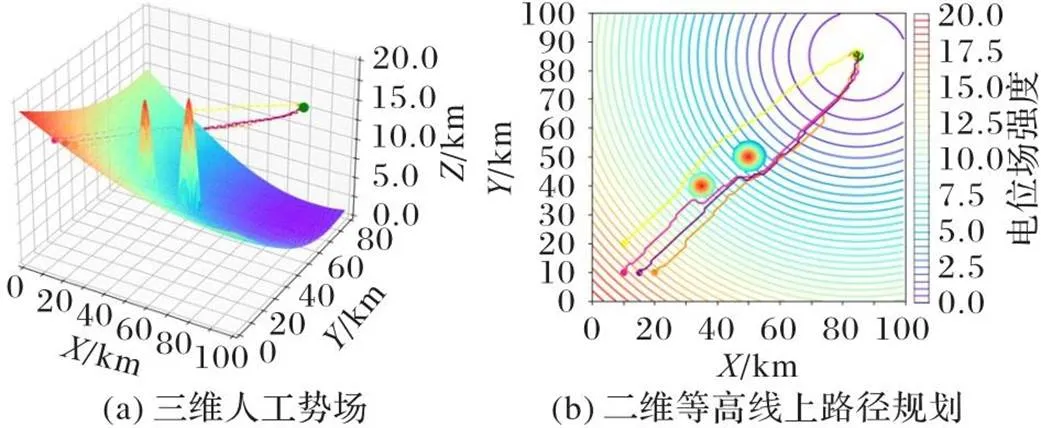
图7　DCPSO算法的路径规划

图8则直观地展示了DCPSO优化后的无人机集群路径规划，从中可以看出路径真实，无人机集群转弯角度不大。更重要的是，规划的路径可以避开障碍物，保证无人机集群在飞行过程中不会撞到障碍物，极大地保证了无人机集群在实际飞行路径规划过程中的安全。同时，从图8中可以看出，DCPSO的整体搜索效率函数值在初始阶段（大约0～8次迭代）迅速下降。然后，随着迭代次数的增加，搜索效率函数的值最终收敛到257.940。

从图7、8可以看出，DCPSO算法可以使搜索效率函数快速收敛，缩短无人机集群的飞行距离，有效避开障碍物，在最短的时间内到达终点。在收敛速度方面，DCPSO算法是该问题的有效优化方法。

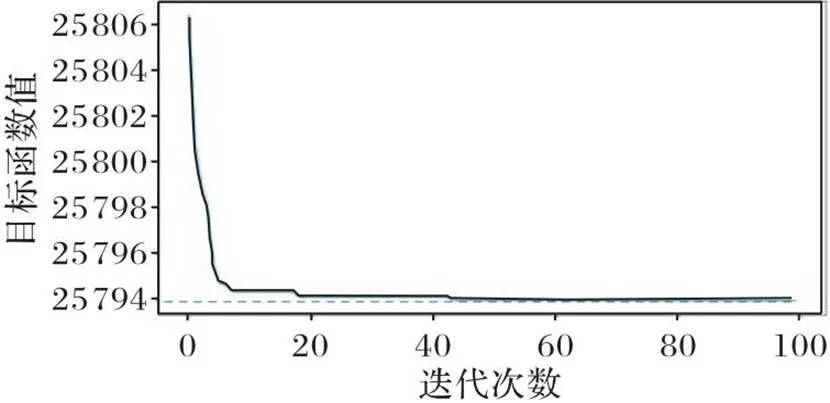
图8　DCPSO算法的收敛曲线

4.2.2有效性

为了验证基于DCPSO的无人机集群路径规划在复杂环境下的有效性，本文在4.2.1节的基础上增加了障碍物的数量。整个飞行区域布置了5个障碍物，坐标如下：（35，40，15）、（50，50，15）、（50，35，15）、（60，70，15）和（68，52，15），其他参数同上。仿真结果如图9所示。从图9可以看出，无人机集群在复杂的环境中仍然可以使用DCPSO算法准确地避开障碍物并到达终点。飞行道路平坦，没有太大的弯道，短且没有长弯路。

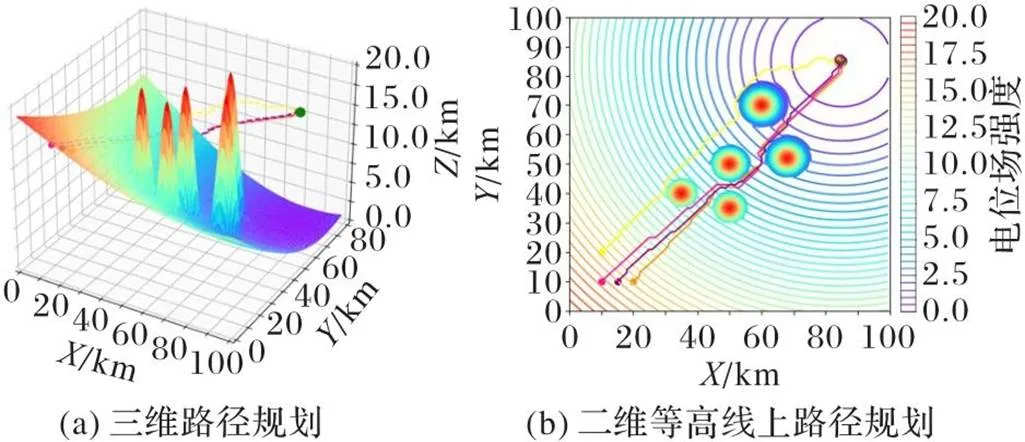
图9　多障碍环境下DCPSO算法的路径规划

4.2.3稳定性

采用蒙特卡罗方法独立运行30次，得到可行路径长度的平均值和标准差，进一步验证DCPSO算法在解决无人机集群路径规划中的稳定性和有效性。实验结果如表7所示。

通过分析表7中的仿真结果，经DCPSO优化的轨道长度在30次独立重复实验中的平均值、标准偏差、最优值和最差值分别为108.984 6、0.384 1、108.234 5和109.855 8。可以看出，DCPSO算法优化后的无人机集群路径规划结果波动小，稳定性高，验证了DCPSO算法在实际应用中的稳定性和鲁棒性。

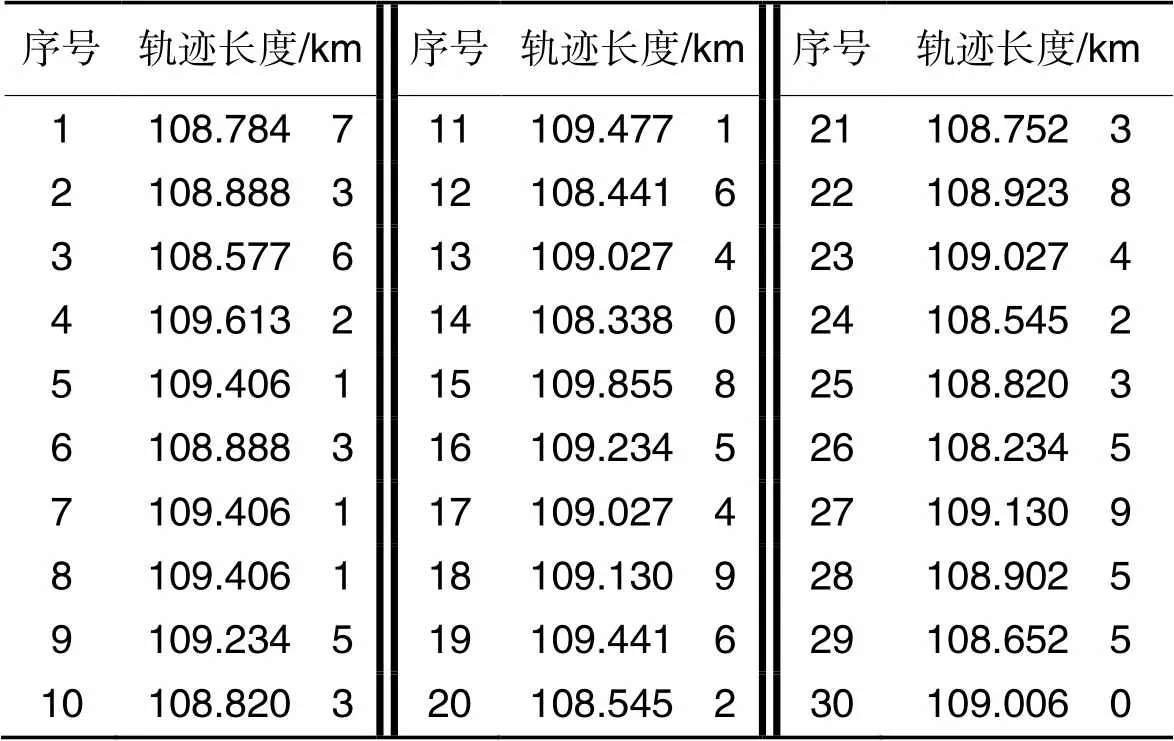
表7　DCPSO算法进行30次独立重复实验的结果

5 结语

针对PSO局部精度不高、易陷入局部最优的问题，综合动态簇机制和混沌初始化思想，提出一种动态簇粒子群优化（DCPSO）算法，并根据实际应用场景，将DCPSO应用于无人机集群路径规划问题，以提高无人机集群的执行效率。

与标准的PSO算法相比，DCPSO算法在保留PSO算法原有优势的基础上，对它们全局搜索能力和鲁棒性进行优化，并通过仿真实验验证了它是一种很有潜力的群体智能优化算法。

在复杂的三维仿真环境中，DCPSO算法在无人机集群路径规划问题上被证明是可行和有效的，进一步验证了算法具有很高的适应性和稳定性。

综上所述，DCPSO算法具有较大的竞争优势和应用前景。未来，各种应用场景将需要无人机集群在更复杂多样的飞行环境中运行，自适应稳定的无人机集群路径规划是一个重要的研究方向。

[1] LYU H， YIN Y. Fast path planning for autonomous ships in restricted waters［J］. Applied Sciences， 2018， 8（12）： No.2592.

[2] VOLKAN PEHLIVANOGLU Y. A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of autonomous UAV［J］. Aerospace Science and Technology， 2012， 16（1）： 47-55.

[3] XUE J， SHEN B. A novel swarm intelligence optimization approach： sparrow search algorithm［J］. Systems Science and Control Engineering， 2020， 8（1）： 22-34.

[4] DUAN H， QIAO P. Pigeon-inspired optimization： a new swarm intelligence optimizer for air robot path planning［J］. International Journal of Intelligent Computing and Cybernetics， 2014， 7（1）： 24-37.

[5] BHARNE P K， GULHANE V S， YEWALE S K. Data clustering algorithms based on swarm intelligence［C］// Proceedings of the 3rd International Conference on Electronics Computer Technology. Piscataway： IEEE， 2011： 407-411.

[6] KENNEDY J， EBERHART R. Particle swarm optimization［C］// Proceedings of the 1995 International Conference on Neural Networks — Volume 4. Piscataway： IEEE， 1995： 1942-1948.

[7] 鲁亮亮，代冀阳，应进，等. 基于APSODE-MS算法的无人机航迹规划［J］. 控制与决策， 2022， 37（7）：1695-1704.（LU L L， DAI J Y， YING J， et al. UAV trajectory planning based on APSODE-MS algorithm［J］. Control and Decision， 2022， 37（7）： 1695-1704.）

[8] NAYEEM G M， FAN M， AKHTER Y. A time-varying adaptive inertia weight based modified PSO algorithm for UAV path planning［C］// Proceedings of the 2nd International Conference on Robotics， Electrical and Signal Processing Techniques. Piscataway： IEEE， 2021： 573-576.

[9] LI X， ZHAO Y， ZHANG J， et al. A hybrid PSO algorithm based flight path optimization for multiple agricultural UAVs［C］// Proceedings of the IEEE 28th International Conference on Tools with Artificial Intelligence. Piscataway： IEEE， 2016： 691-697.

[10] 田兴华，张纪会，李阳. 基于混沌映射的自适应退火型粒子群算法［J］. 复杂系统与复杂性科学， 2020， 17（1）：45-54.（TIAN X H， ZHANG J H， LI Y. An adaptive annealing particle swarm optimization based on chaotic mapping ［J］. Complex Systems and Complexity Science， 2020， 17（1）： 45-54.）

[11] ZHANG R， SUN M， PAN C. Micro-nano satellite resource allocation algorithm based on chaos-filled PSO ［C］// Proceedings of the 6th International Symposium on Computer and Information Processing Technology. Piscataway： IEEE， 2021： 204-208.

[12] KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots ［J］. The International Journal of Robotics Research， 1986， 5（1）： 90-98.

[13] 段海滨，杨之元. 基于柯西变异鸽群优化的大型民用飞机滚动时域控制［J］. 中国科学：技术科学， 2018， 48（3）：277-288.（DUAN H B， ZHANG Z Y. Large civil aircraft receding horizon control based on Cauthy mutation pigeon inspired optimization ［J］. SCIENTIA SINICA Technologica， 2018， 48（3）： 277-288.）

[14] LIANG X， WANG D， HUANG M. Improved grey wolf optimizer and their applications［C］// Proceedings of the IEEE 7th International Conference on Computer Science and Network Technology. Piscataway： IEEE， 2019： 107-110.

[15] XU S， XU D， MAO Y， et al. A cooperative dynamic cluster in multitasking mobile networks ［J］. Intelligent Automation and Soft Computing， 2017， 23（4）： 567-572.

[16] LI L， XU S， NIE H， et al. Collaborative target search algorithm for UAV based on chaotic disturbance pigeon-inspired optimization［J］. Applied Sciences， 2021， 11（16）： No.7358.

Route planning method of UAV swarm based on dynamic cluster particle swarm optimization

WANG Longbao1，2， LUAN Yinqi1， XU Liang3， ZENG Xin3， ZHANG Shuai4， XU Shufang1，2*

（1，，211100，；2（），211100，；3，430014，；4，650051，）

Route planning is very important for the task execution of Unmanned Aerial Vehicle （UAV） swarm， and the computation is usually complex in high dimensional scenarios. Swarm intelligence has provided a good solution for this problem. Particle Swarm Optimization （PSO） algorithm is especially suitable for route planning problem because of its advantages such as few parameters， fast convergence and simple operation. However， PSO algorithm has poor global search ability and is easy to fall into local optimum when applied to route planning. In order to solve the problems above and improve the effect of UAV swarm route planning， a Dynamic Cluster Particle Swarm Optimization （DCPSO） algorithm was proposed.Firstly， artificial potential field method and receding horizon control principle were used to model the task scenario of route planning problem of UAV swarm. Secondly， Tent chaotic map and dynamic cluster mechanism were introduced to further improve the global search ability and search accuracy. Finally， DCPSO algorithm was used to optimize the objective function of the model to obtain each trajectory point selection of UAV swarm. On 10 benchmark functions with different combinations of unimodal/multimodal and low-dimension/high-dimension， simulation experiments were carried out. The results show that compared with PSO algorithm， Pigeon-Inspired Optimization （PIO）， Sparrow Search Algorithm （SSA） and Chaotic Disturbance Pigeon-Inspired Optimization （CDPIO） algorithm， DCPSO algorithm has better optimal value， mean value and variance， better search accuracy and stronger stability. Besides， the performance and effect of DCPSO algorithm were demonstrated in the route planning application instances of UAV swarm simulation experiments.

Particle Swarm Optimization (PSO); dynamic cluster mechanism; Unmanned Aerial Vehicle (UAV) swarm; route planning; receding horizon control

This work is partially supported by Major Science and Technology Special Program of Yunnan Province Science and Technology Department （202202AF080003）， Scientific Research Project of Yangtze Ecology and Environment Company Limited （HBZB2022005）.

WANG Longbao， born in 1977， Ph. D.， senior engineer. His research interests include domain software， intelligent computing.

LUAN Yinqi， born in 2000， M. S. candidate. Her research interests include intelligent computing.

XU Liang， born in 1980， senior engineer. His research interests include construction management of ecological and environmental protection projects.

ZENG Xin， born in 1990， engineer. His research interests include construction and management of ecological and environmental protection projects.

ZHANG Shuai， born in 1988， senior engineer. His research interests include information fusion.

XU Shufang， born in 1981， Ph. D.， associate professor. Her research interests include wireless communication network， information fusion.

TP391.9

A

1001-9081（2023）12-3816-08

10.11772/j.issn.1001-9081.2022111763

2022⁃11⁃28；

2023⁃03⁃26；

2023⁃03⁃30。

云南省科技厅重大科技专项计划项目（202202AF080003）；长江生态环保集团有限公司科研项目（HBZB2022005）。

王龙宝（1977—），男，江苏盐城人，高级工程师，博士，CCF会员，主要研究方向：领域软件、智能计算；栾茵琪（2000—），女，山东菏泽人，硕士研究生，主要研究方向：智能计算；徐亮（1980—），男，江西九江人，高级工程师，主要研究方向：生态环保工程建设管理；曾昕（1990—），男，湖北十堰人，工程师，主要研究方向：生态环保工程建设管理；张帅（1988—），男，云南昆明人，高级工程师，主要研究方向：信息融合；徐淑芳（1981—），女，安徽青阳人，副教授，博士，主要研究方向：无线通信网络、信息融合。