对比保序模式挖掘算法

孟玉飞，武优西*，王珍，李艳

对比保序模式挖掘算法

孟玉飞1，武优西1*，王珍1，李艳2

（1.河北工业大学 人工智能与数据科学学院，天津 300401； 2.河北工业大学 经济管理学院，天津 300401）（∗通信作者电子邮箱wuc567@163.com）

针对现有的对比序列模式挖掘方法主要针对字符序列数据集且难以应用于时间序列数据集的问题，提出一种对比保序模式挖掘（COPM）算法。首先，在候选模式生成阶段，采用模式融合策略减少候选模式数；其次在模式支持度计算阶段，利用子模式的匹配结果计算超模式的支持度；最后，设计了动态最小支持度阈值的剪枝策略，以进一步有效地剪枝候选模式。实验结果表明，在6个真实的时间序列数据集上，在内存消耗方面，COPM算法至少比COPM-o（COPM-original）算法降低52.1%，比COPM-e（COPM-enumeration）算法低36.8%，比COPM-p（COPM-prune）算法降低63.6%；同时在运行时间方面，COPM算法至少比COPM-o算法降低30.3%，比COPM-e算法降低8.8%，比COPM-p算法降低41.2%。因此，在算法性能方面，COPM算法优于COPM-o、COPM-e和COPM-p算法。实验结果验证了COPM算法可以有效挖掘对比保序模式，发现不同类别的时间序列数据集间的差异。

模式挖掘；序列模式挖掘；时间序列；对比模式；保序模式

0 引言

随着大数据时代的发展，时间序列数据广泛存在于各领域，如股票每日收盘价［1］、每日的天气温度［2］、心/脑电数据［3］等。时间序列包含大量对用户有用的信息，具有广泛的应用价值。人们迫切希望从时间序列数据中挖掘有用的模式。传统的时间序列研究方法通常先采用分段聚合近似（Piecewise Aggregate Approximation， PAA）［4］和符号聚合近似（Symbolic Aggregate approXimation， SAX）［5］等方法将数值数据符号化，再研究挖掘字符序列的序列模式挖掘方法。然而时间序列的字符化在实现的过程中不仅会引入噪声，还会忽略序列的原始趋势特征，难以描述时间序列数据中的关键趋势特征。

为了解决上述问题，Kim等［6］提出了保序模式的概念，直观地表示时间序列中的波动趋势。近年来，保序模式匹配研究得到了较多学者的关注［7］，并提出了多种保序模式匹配算法，如高效的保序模式匹配算法［8］、近似保序模式匹配算法［9］等；但是这些方法需要用户预先给定查询模式［10-11］，从而在时间序列中寻找查询模式的出现位置。为了有效地从时间序列中发现频繁出现的相同趋势，Wu等［12］首次提出保序模式挖掘问题。为了提高算法的挖掘效率，并进一步提高保序模式的推荐准确率，Wu等［13］提出了保序规则模式挖掘算法。

但是上述挖掘方法主要在时间序列上挖掘频繁模式，在挖掘过程中未考虑不同类别的时间序列之间差异显著时的对比模式。受符号序列的对比模式挖掘算法［14］的启发，本文在时间序列数据上探索了对比保序模式挖掘（Contrast Order-preserving Pattern Mining， COPM），并提出一种高效的COPM算法，该算法可以有效地发现不同类别时间序列数据集的差异。

本文的主要工作如下：

1）在候选模式生成方面，采用模式融合策略，大幅减少了候选模式数。

2）在支持度计算（Support Calculation， SC）方面，COPM算法使用子模式匹配结果计算超模式的支持度，大幅缩短了运行时间，降低了时间复杂度。

3）在对比保序模式判定方面，提出了一种动态最小支持度阈值的剪枝策略，以缩短运行时间。

4）在真实的时间序列数据集上进行了对比实验，验证了COPM算法的有效性。

1 相关工作

序列模式挖掘作为数据挖掘的一个重要分支［15-17］，在诸如差分隐私保护［18］等领域得到了广泛的应用。由于传统的序列模式挖掘方法在现实生活中存在诸多问题和局限性，因此研究者们针对用户的不同需求提出了多种扩展方法，如间隙约束序列模式挖掘［19-21］、闭合序列模式挖掘［22］、共生序列模式挖掘［23-25］、高效用序列模式挖掘［26-28］、负序列模式挖掘［29-30］和面向用户兴趣的三支序列模式挖掘［31］；但是，当前序列模式挖掘方法只关注模式在序列中的出现数，并未考虑序列的类别信息，导致一些重要模式的丢失。针对此问题，研究者们提出了一些新的模式和挖掘方法，如对比模式挖掘［32-36］的方法旨在找到在一些类别中频繁出现，但在其他类别中不频繁出现的序列模式，可被应用在序列数据集中分析用户行为。

目前大多数经典的序列模式挖掘算法主要关注离散字符序列，不能直接应用于时间序列数据。由于时间序列具有高维、海量等结构特征，使用传统的挖掘方法不仅会降低算法性能，还会影响最终模式挖掘结果的准确性和有效性。近些年，时间序列挖掘成为数据挖掘的热点，各种模式匹配或模式挖掘方法被提出。例如，三支序列模式挖掘将时间序列的波动趋势分为强、中和弱，而用户通常比较关心的是由强和中趋势组成的模式［31］。为了避免查询模式与时间序列之间存在较大偏差，Li等［9］提出了近似序列模式挖掘方法，在进行模式匹配和挖掘前，通常使用离散化方法（如分段线性表示方法和符号表示方法）降维处理时间序列的数据。以上方法都采用了一些符号方法将时间序列转换为符号。

虽然符号化表示方法能够将时间序列离散化成字符后进行挖掘，但是符号化方法容易引入噪声，并且符号化方法过于关注时间序列中的数值，忽略了时间序列上的趋势变化。近期，研究人员提出了保序模式匹配方法［6］，该方法无需进行数学变换和符号化，直接使用数值的相对顺序表示时间序列中元素的秩，能够直观地表示时间序列中的波动趋势。受保序模式匹配的启发，武优西等［37］提出了一种新的时间序列模式挖掘方法——保序序列模式挖掘，它重点关注时间序列上的波动趋势，能够找出给定时间序列中的所有的频繁保序模式；但该方法在计算模式支持度的过程中，需要多次扫描数据库，算法效率低。为了进一步提高算法的效率，武优西等［38］提出了一种保序序列规则挖掘方法，在挖掘过程中利用子模式的匹配结果计算超模式的支持度，提高了挖掘效率。这两种挖掘方法只是挖掘最精确的保序序列模式，为了满足不同场景的需要，武优西等［39］又提出了一种近似保序序列模式挖掘方法，以挖掘近似程度不同的保序模式。

然而，在上述研究中，保序模式挖掘、保序序列规则挖掘方法和近似保序序列模式挖掘都只在单类别时间序列数据集上挖掘，忽略了不同类别数据间的差异性，为了有效地发现不同类别时间序列数据集的差异，本文提出了一种COPM算法。

2 问题定义

时间序列数据库是由多条时间序列组成的大型时间序列数据集，可以表示为＝｛1，2，…，T，…，T｝，其中T是由一组数字元素组成的序列。

定义2 秩次。一组中某个值的秩次是它在组中的排列顺序，记作（p）。

定义3 保序模式。一组由秩次表示的模式称为保序序列模式，简称保序模式，记作（）=（（1），（2），…，（p））。

例1 给定时间序列=｛15，10，18，12，19，14｝，它的子序列是一个模式，即=（15，10，18，12）。

其中元素15在中是第三小的，那么（15）=3；同理，（10）=1，（18）=4，（12）=2，因而，（）=（3，1，4，2）。

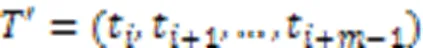
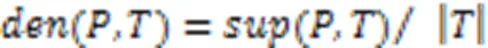
定义6 支持率。如果（，）大于给定的密度阈值，那么，计数为1；否则，计数为0。模式在时间分类序列库中的支持率是所有时间序列的计数和与时间序列数之比，记作（，）。

定义7 对比保序模式。为了反映两类时间序列的差异，对正类设定最小支持率阈值；并对负类设定最大支持率阈值，如果模式同时满足以下两个条件，则称模式是一个对比保序模式。

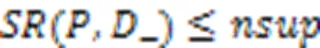
3 本文算法

3.1　候选模式生成

候选模式生成的策略主要有枚举策略和模式融合策略两种。本节采用模式融合策略生成候选模式。文献［12］中的模式融合策略可以有效地减少候选模式数，相关定义如下。

定义8 前缀保序模式、后缀保序模式、保序子模式和保序超模式。给定模式=（1，2，…，p），子模式=（（1，2，…，p-1））称为模式的前缀保序模式，记作=（）；子模式=（（2，3，…，p））称为模式的后缀保序模式，记作=（）。同时，和成为的保序子模式，称为模式和的保序超模式。

定义9 模式融合。给定两个长度的保序模式、，若（）=（），那么模式和可以生成长度为+1的超模式。存在两种情况：

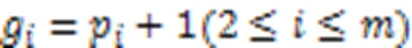
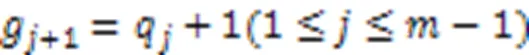
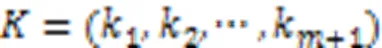
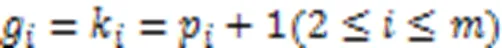
例2介绍生成候选模式的策略。

例2 给定模式=（1，3，2），=（2，1，3），可以生成长度为4的候选模式。

如果将作为前缀模式，作为后缀模式，候选模式生成规则如下：以（1，3，2）⊕（2，1，3）为例，（）=（）=（2，1），且1≠3，满足情况1，可以生成1个长度为4的候选模式=⊕。由于1<3，因此1=1，4=3+1=4；由于2<4，因此2=2=3；由于3<4，因此3=3=2。可以得知，=（1，3，2，4）。

如果将作为前缀模式，作为后缀模式，候选模式生成规则如下：以（2，1，3）⊕（1，3，2）为例，（）=（）=（1，2），且1=3，满足情况2，可以生成2个长度为4的候选模式，=⊕。由融合规则可得，=（2，1，4，3），=（3，1，4，2）。

另外一种生成候选模式的策略是枚举策略，每个长度为的模式可以生成+1个候选模式。若对例2采用枚举法，则每个模式都可以生成4个候选模式，以为例，得到的候选模式为（2，4，3，1）、（1，4，3，2）、（1，4，2，3）和（1，3，2，4），则模式（1，3，2）和（2，1，3）将生成8个候选模式；然而，模式（1，3，2）和（2，1，3）采用模式融合策略仅生成3个候选模式，因此模式融合策略可以有效地减少候选模式数。

3.2　支持度计算

为了避免冗余计算，支持度计算的策略主要是利用子模式的匹配结果计算超模式的支持度，以缩短运行时间。下面将给出具体的计算规则。

挖掘保序模式从长度为2的模式开始，因为长度为1的模式只是一个点，没有趋势波动，长度为2的模式只有两个点（1，2）和（2，1）。扫描一遍时间序列，如果子序列的相对顺序为（1，2），则将它的位置索引存入（1，2）；否则，存入（2，1）。

当模式长度大于2时，采用3.1节的模式融合策略生成候选模式，由于⊕生成候选模式时有两种情况，因此，计算模式支持度也对应两种情况。

作为前缀保序子模式、作为后缀保序子模式时，对应的匹配集合分别为L，T和L，T。生成的候选超模式对应的匹配集合则为L，T和L，T。

情况1=⊕。

情况2，=⊕。

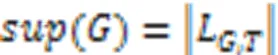
下面通过例3介绍上述模式支持度计算规则。

例3 给定时间序列1=｛15，10，18，12，19，14｝，以及长度为2的保序模式=（1，2）和=（2，1）。

子序列（10，18）和（12，19）对应的保序模式为（1，2），因此将它的位置索引（3，5）存入（1，2）；子序列（15，10）、（18，12）和（19，14）对应的保序模式为（2，1），因此将它的位置索引（2，4，6）存入（2，1）。最终通过计算可知，和在时间序列1上的匹配集合分别为L，T1=｛3，5｝和L，T1=｛2，4，6｝。

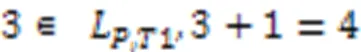
算法1 支持度计算（SC）算法。

输入 前缀保序子模式，后缀保序子模式，以及它们对应的匹配集合L，T和L，T；

输出 超模式的支持度。

3） 根据情况2得到匹配集合L，T和L，T

4） ELSE

5） 根据情况1得到匹配集合L，T

6） END IF

7） RETURN（G，T）.，（K，T）.

3.3　COPM算法

为了更高效地挖掘对比保序模式，本节设计一个剪枝策略剪枝候选模式，并提出COPM算法。

动态最小支持度阈值的剪枝策略为：若（，+）<，则将模式以及它的超模式剪枝。

COPM算法的具体步骤如下：

步骤1 扫描一次时间序列数据库。

步骤2 得到（1，2）和（2，1）模式的匹配集合（（1，2），D）和（（2，1），D），并将（1，2）和（2，1）加入候选模式集C（=2）。

步骤3 根据模式融合策略，由C生成长度为+1的候选超模式。

步骤4 利用SC算法计算模式的支持度，继而根据剪枝策略进行剪枝；若不被剪枝，则将它加入候选模式集C。最终若为对比保序模式，则将该模式加入结果集。

步骤5 重复执行步骤3～4，直到没有新的候选模式生成。

步骤6 最终得到所有符合条件的对比保序模式结果集。

例4 给定时间序列数据库，如表1所示。序号为1～3的时间序列为一组，即某一类时间序列库，类别标签用+表示；序号为4～6的时间序列为另一组，即另一类时间序列库，类别标签用-表示。设置最小密度阈值=0.1，正类最小支持率阈值=0.5，负类最大支持率阈值=0.1，挖掘中所有的对比保序模式。

表1时间序列数据库示例

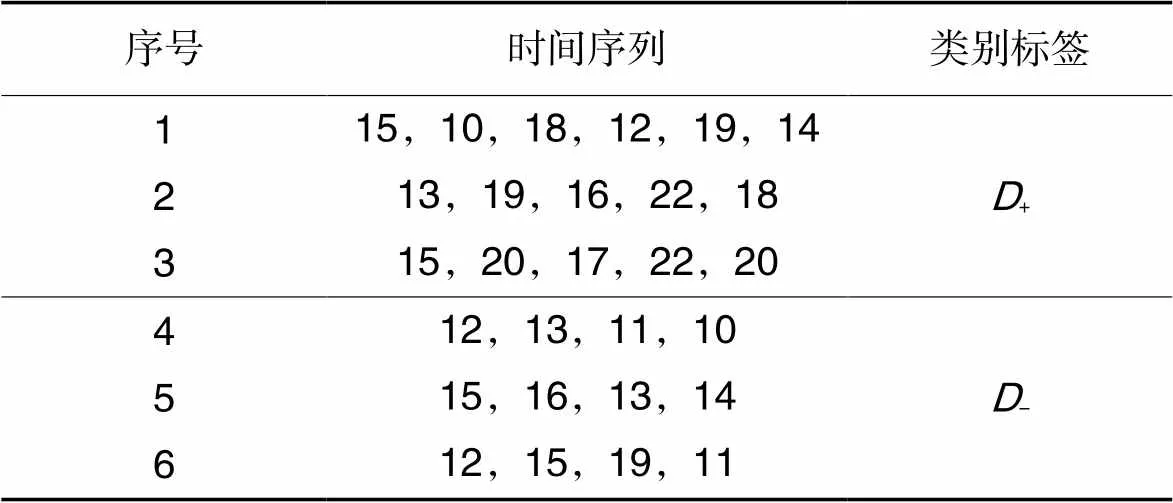
Tab.1　Example of time series database D

注：序号1～6代表有6条时间序列。

根据步骤1，扫描时间序列数据库。

根据步骤2，可以得到（（1，2），D）和（（2，1），D），并得到2=｛（1，2），（2，1）｝。

根据步骤3，由长度为2的模式（1，2）和（2，1）可以生成长度为3的候选模式（1，2，3）、（1，3，2）、（2，3，1）、（2，1，3）、（3，1，2）和（3，2，1）。

根据步骤4，利用SC算法计算支持度。以模式=（1，3，2）为例，通过SC算法计算可知模式在1、2、3、4、5和6中的支持度分别为2、2、2、0、0和0。再根据定义5，可以计算得出模式在1、2、3、4、5和6中的密度值分别为0.33、0.4、0.4、0、0和0。最后根据定义6计算可知，（，+）=3/3=1，（，-）=0/3=0。由于1>，则不会被剪枝，将模式加入候选模式集3；且0<，则模式符合对比保序模式定义。因此，模式是一个对比保序模式，将模式（1，3，2）加入结果集。

根据步骤5，重复执行步骤3和4，直到没有新的候选模式生成，最终得到所有符合条件的对比保序模式集为=｛（1，3，2），（2，1，3），（1，3，2，4），（3，1，4，2），（1，4，2，5，3）｝。

算法2 COPM算法。

输入 时间序列数据库，最小密度阈值，正类最小支持率阈值，负类最大支持率阈值；

输出 对比保序模式结果集。

1） 扫描一次时间序列数据库，得到（（1，2），D）和（（2，1），D），并得到2=｛（1，2），（2，1）｝

2）←2

3） WHILEC！= null DO

4） FOR eachinCDO

5） FOR eachinCDO

6） IFcan fuse withTHEN

7） 根据模式融合策略生成超模式

8） 利用SC算法计算超模式的支持度，再根据定义5、6得到超模式支持率（，+）

9） IF（，+）≥THEN

10） 将模式加入候选模式集C+1，再计算（，-）

11） IF（，-）≤THEN

12） 将模式加入结果集

13） END IF

14） END IF

15） END IF

16） END FOR

17） END FOR

18）←+1；

19） END WHILE

20） RETURN

4 实验与结果分析

4.1　实验数据集

为了验证COPM算法的性能，本文采用真实的时间序列数据集作为测试数据集，数据集中的数据分为两类。所有的数据集都可以在http：//www.timeseriesclassification.com/dataset.php网站下载。表2给出了每个数据集的具体描述。

表2实验数据集

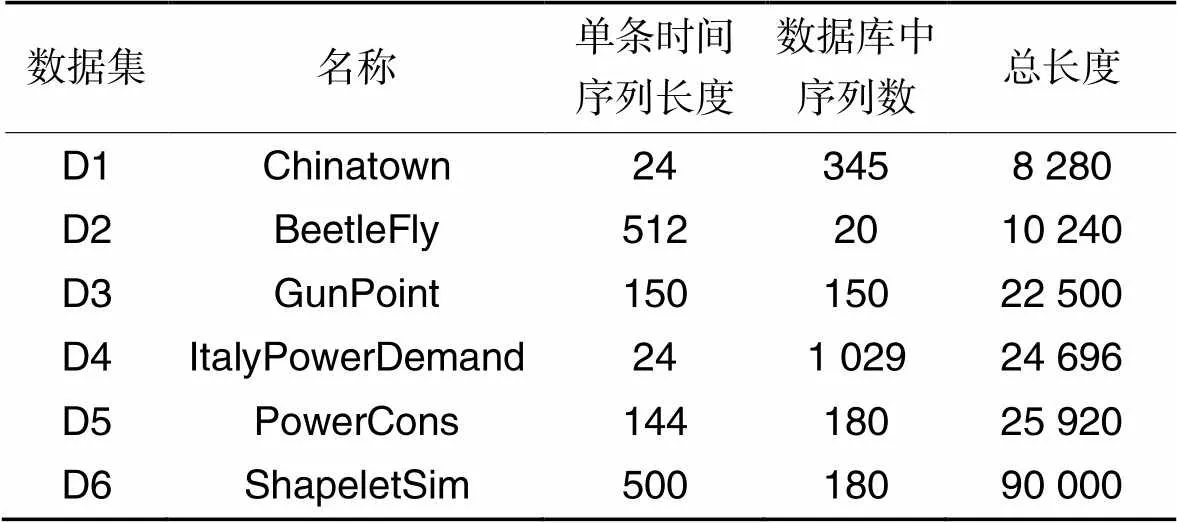
Tab.2　Experimental datasets

实验运行的环境为：Inter Core i5-3230U处理器，主频1.60 GHz，内存8 GB，Windows 10，64位操作系统，程序的开发环境为Eclipse。

4.2　对比算法

1）COPM-o（COPM-original）。为了分析COPM算法计算支持率的效率，提出了COPM-o算法，该算法采用Wu等［12］提出的保序模式匹配方法计算候选模式支持率。

2）COPM-e（COPM-enumeration）。为了分析模式融合策略的性能，提出了COPM-e算法，该算法采用枚举策略生成候选模式。

3）COPM-p（COPM-prune）。为了验证2.3节中的剪枝策略的效果，提出了COPM-p算法，该算法未采用该剪枝策略。

4.3　COPM算法的挖掘效果

为了验证COPM算法的有效性，本文采用COPM-o、COPM-e和COPM-p这3个对比算法。在D1～D6这6个数据集上实验，设置=0.01，=0.25，=0.1。表3分别给出在数据集D1～D6上的内存消耗、运行时间和候选模式数的对比。在D1～D6数据集上，在内存消耗方面，COPM算法至少比COPM-o算法降低52.1%，比COPM-e算法降低36.8%，比COPM-p算法降低63.6%；同时在运行时间方面，COPM算法至少比COPM-o算法降低30.3%，比COPM-e算法降低8.8%，比COPM-p算法降低41.2%。通过观察表3可以得到如下结论：

1）COPM算法优于COPM-o算法，因为COPM算法不仅比COPM-o算法消耗更少的内存，而且运行时间更短，这表明COPM算法采用了比COPM-o算法更有效的策略计算支持率，即本文的支持度计算方法能够缩短运行时间。例如，从表3可以看出，在D1上，两种算法都生成了161个候选模式，在D1上，COPM算法消耗内存16.284 MB，花费了0.165 s；而COPM-o算法消耗内存为67.451 MB，花费了0.607 s。在其他数据集上也可以发现同样结果。原因如下：COPM-o算法采用的模式匹配的策略不能很好地利用子模式的计算结果，必须重复扫描数据库，导致计算效率低；相反，COPM算法只需扫描一次数据库，并且利用子模式的计算结果计算超模式的支持度，避免了许多冗余的计算，从而缩短运行时间。因此，COPM算法优于COPM-o算法。

2）COPM算法优于COPM-e算法，这表明模式融合策略可以有效地剪枝候选模式。从表3可以看出，COPM算法比COPM-e算法消耗更少的内存，且COPM算法比COPM-e算法运行时间更短。例如，在D1上，COPM算法消耗内存16.284 MB，花费时间为0.165 s。而COPM-e算法消耗内存29.905 MB，花费时间为0.221 s。其他数据集上也是同样的效果。原因如下：模式融合策略可以有效地剪枝候选模式。例如，从表3可以看出，在D1上，COPM算法生成了161个候选模式，而COPM-e算法生成了235个候选模式，与COPM算法相比，COPM-e算法生成的候选模式数多了45.9%。候选模式数越少，算法运行越快，算法消耗的内存越少；因此，COPM算法优于COPM-e算法。

3）COPM算法优于COPM-p算法，这表明剪枝策略能进一步缩短运行时间。从表3可以看出，在所有数据集上COPM算法均比COPM-p算法消耗更少的内存，并且花费更少的运行时间。例如，在D1上，COPM算法消耗内存为16.284 MB，花费时间为0.165 s；而COPM-p算法消耗内存为189.285 MB，花费时间为336.734 s。这是因为剪枝策略可以有效地减少候选模式数。在D1上，COPM-p算法生成的候选模式数为29 925，而COPM算法生成的候选模式数仅为161，与COPM算法相比，COPM-p算法生成的候选模式数量多了99.5%，因此，COPM算法优于COPM-p算法。

表3不同算法在数据集D1～D6上不同指标对比

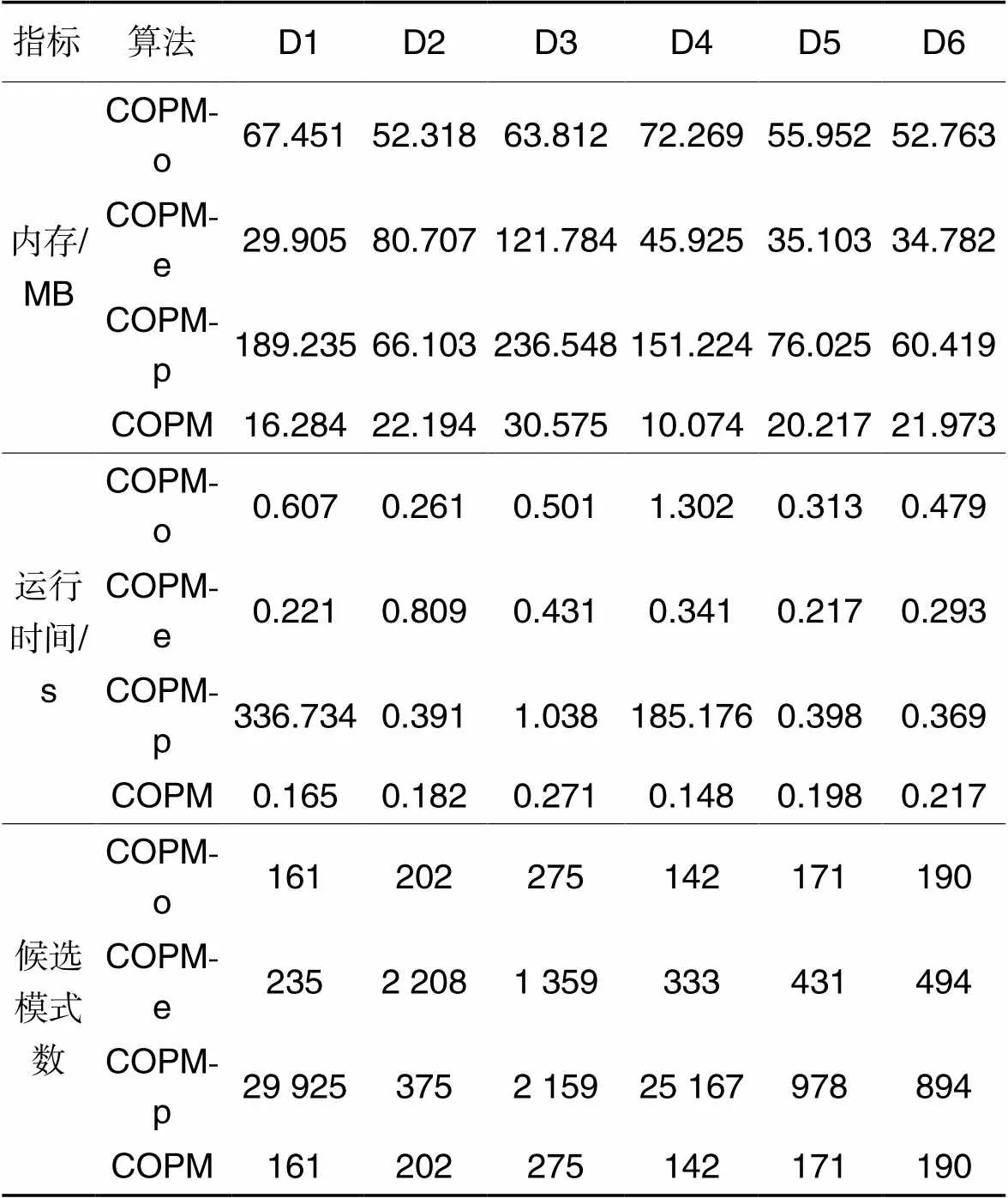
Tab.3　Comparison of different algorithms with different indicators on dataset D1 to D6

4.4　可扩展性

为了验证COPM算法的可扩展性，本文采用COPM-o、COPM-e和COPM-p算法作为对比算法；此外，选择D6数据集作为实验基础数据集，并且创建了D6_1，D6_2，D6_3，D6_4，D6_5和D6_6实验数据集，它们分别是D6数据集大小的1、2、3、4、5和6倍。参数设置为=0.01，=0.25，=0.1。内存消耗和运行时间的结果对比分别如表4所示。

表4不同数据集大小下的内存消耗和运行时间对比

Tab.4　Comparison of memory consumption and running time with different dataset sizes

由表4可知，COPM算法的内存消耗和运行时间都随数据集大小的增加呈线性增长。例如，与D6_1相比，D6_6的长度增加了500%，COPM算法在D6_1上内存消耗为21.973 MB，而在D6_6上内存消耗为94.395 MB，与D6_1相比，COPM算法在D6_6上的内存消耗增长了329.6%，在D6_1上运行时间为0.217 s，而在D6_6上运行时间为0.923 s，与D6_1相比，COPM算法在D6_6上的运行时间增加了325.4%。因此，内存消耗和运行时间的增加明显慢于数据集大小的增长。这些结果表明，COPM算法的时间和空间复杂度与数据集大小呈正相关。在其他数据集也有相同的规律。更重要地，在所有数据集上，COPM算法的挖掘性能比其他对比算法更优，COPM算法的内存消耗明显少于其他对比算法，并且运行时间比其他对比算法都更短。因此，根据COPM算法的挖掘性能不会随着数据集大小的增加而降低，进而可以得出结论，COPM算法具有很强的可扩展性。

4.5　不同密度阈值对算法性能的影响

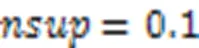
从图1、2可以看出，一般情况下，随着密度阈值的增大，COPM算法生成的候选模式数更少，运行时间更短。例如，在D3上，当=0.01和=0.025时，运行时间分别是0.271 s和0.170 s；生成的候选模式数分别为275和118。产生这一现象的原因如下：随着值的增加，密度值大于最小密度阈值的候选模式数显著减少，使算法运行时间更短。

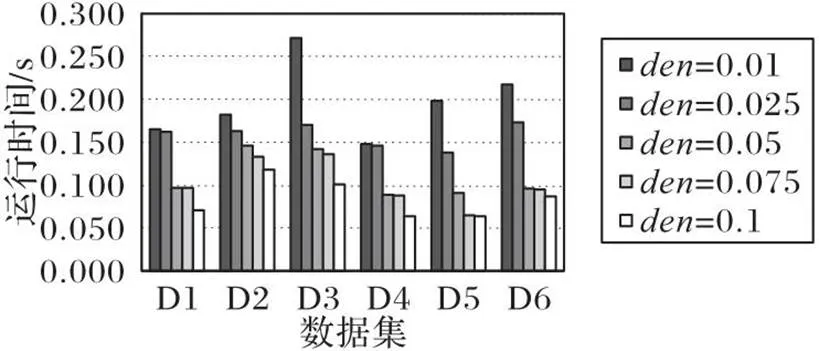
图1　D1～D6上不同den值下的运行时间对比

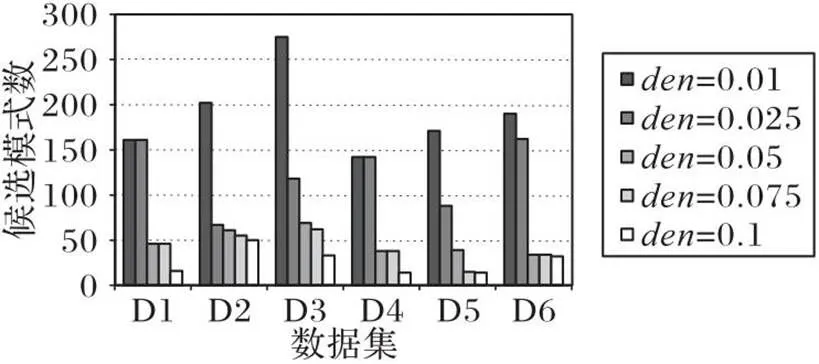
图2　D1～D6上不同den值下的候选模式数对比

5 结语

本文提出了一种基于时间序列数据库的COPM算法，可以发现不同类别时间序列数据集间的差异性。该算法主要分为候选模式生成和支持度计算两个步骤：在候选模式生成阶段，本文采用模式融合策略，大幅减少了候选模式数；在支持度计算阶段，本文利用子模式的匹配结果计算超模式的支持度，避免了重复扫描数据库，大幅缩短了算法的运行时间。为了进一步有效地挖掘对比保序模式，提出了动态最小支持率阈值的剪枝策略进一步减少候选模式数，以减少算法的运行时间。通过与3个对比算法对比实验，得出了COPM算法在内存消耗、运行时间和候选模式生成方面的性能均优于其他算法，验证了COPM算法具有较强的可扩展性。本文还验证了不同密度阈值对算法性能的影响。综上所述，本文的实验结果均验证了COPM算法的有效性。

多分类问题可以通过一对多的方式或者树形多级的方式转换为多个二分类问题，因此，针对多类数据集挖掘问题，可以采用多次二分类的方式进行对比模式挖掘；但是该挖掘方式过于复杂，未来将进一步研究如何直接在多分类数据集上进行对比模式挖掘；此外，我们还将继续研究如何有效地应用挖掘结果指导分类。

[1] LIN Y， LIN Z X， LIAO Y， et al. Forecasting the realized volatility of stock price index： a hybrid model integrating CEEMDAN and LSTM ［J］. Expert Systems with Applications， 2022， 206： 117736.

[2] MAN J， DONG H H， GAO J Y， et al. GA-GRGAT： a novel deep learning model for high-speed train axle temperature long term forecasting ［J］. Expert Systems with Applications， 2022， 202： 117033.

[3] DAI C L， WU J， PI D C， et al. Brain EEG time-series clustering using maximum-weight clique ［J］. IEEE Transactions on Cybernetics， 2022， 52（1）： 357-371.

[4] CHAKRABARTI K， KEOGH E， MEHROTRA S， et al. Locally adaptive dimensionality reduction for indexing large time series databases ［J］. ACM Transactions on Database Systems， 2002， 27（2）： 188-228.

[5] LIN J， KEOGH E， WEI L， et al. Experiencing SAX： a novel symbolic representation of time series ［J］. Data Mining and Knowledge Discovery. 2007， 15（2）： 107-144.

[6] KIM J， EADES P， FLEISCHER R， et al. Order-preserving matching ［J］. Theoretical Computer Science， 2014， 525（13）： 68-79.

[7] 武优西，刘茜，闫文杰，等. 无重叠条件严格模式匹配的高效求解算法［J］. 软件学报， 2021， 32（11）： 3331-3350.（WU Y X， LIU X， YAN W J， et al. Efficient algorithm for solving strict pattern matching under nonoverlapping condition ［J］. Journal of Software， 2021， 32（11）： 3331-3350.）

[8] CHO S， NA J C， PARK K， et al. A fast algorithm for order-preserving pattern matching ［J］. Information Processing Letters， 2015， 115（2）： 397-402.

[9] LI Y， YU L， LIU J， et al. NetDPO：（delta， gamma）-approximate pattern matching with gap constraints under one-off condition ［J］. Applied Intelligence， 2022， 52（11）： 12155-12174.

[10] CHHABRA T， TARHIO J. A filtration method for order-preserving matching ［J］. Information Processing Letters， 2016， 116（2）： 71-74.

[11] KIM Y， KANG M， NA J C， et al. Order-preserving pattern matching with scaling ［J］. Information Processing Letters， 2023， 180： 106333.

[12] WU Y X， HU Q， LI Y， et al. OPP-Miner： order-preserving sequential pattern mining for time series ［EB/OL］. ［2022-02-09］. https：//arxiv.org/pdf/2202.03140.pdf.

[13] WU Y X， ZHAO X Q， LI Y， et al. OPR-Miner： order-preserving rule mining for time series ［EB/OL］. ［2022-12-04］. https：//arxiv.org/pdf/2209.08932.pdf.

[14] WU Y X， WANG Y H， LI Y， et al. Top-self-adaptive contrast sequential pattern mining ［J］. IEEE Transactions on Cybernetics， 2022， 52（11）： 11819-11833.

[15] GAN W S， LIN J C， FOURNIER-VIGER P， et al. A survey of parallel sequential pattern mining ［J］. ACM Transactions on Knowledge Discovery from Data， 2019， 13（3）： 1-34.

[16] OKOLICA J S， PETERSON G L， MILLS R F， et al. Sequence pattern mining with variables ［J］. IEEE Transactions on Knowledge and Data Engineering， 2020， 32（1）： 177-187.

[17] SAMARIYA D， MA J. A new dimensionality-unbiased score for efficient and effective outlying aspect mining［J］. Data Science and Engineering， 2022， 7（2）： 120-135.

[18] 李艳辉，刘浩，袁野，等. 基于差分隐私的频繁序列模式挖掘算法［J］. 计算机应用， 2017， 37（2）： 316-321.（LI Y H， LIU H， YUAN Y， et al. Frequent sequence pattern mining with differential privacy ［J］. Journal of Computer Applications， 2017， 37（2）： 316-321.）

[19] WU Y X， TONG Y， ZHU X Q， et al. NOSEP： nonoverlapping sequence pattern mining with gap constraints ［J］. IEEE Transactions on Cybernetics， 2018， 48（10）： 2809-2822.

[20] 武优西，周坤，刘靖宇，等. 周期性一般间隙约束的序列模式挖掘［J］. 计算机学报， 2017， 40（6）： 1338-1352.（WU Y X， ZHOU K， LIU J Y， et al. Mining sequential patterns with periodic general gap constraints ［J］. Chinese Journal of Computers， 2017， 40（6）： 1338-1352.）

[21] LI Y， ZHANG S， GUO L， et al. NetNMSP： nonoverlapping maximal sequential pattern mining ［J］. Applied Intelligence. 2022， 52（9）： 9861-9884.

[22] WU Y X， ZHU C R， LI Y， et al. NetNCSP： nonoverlapping closed sequential pattern mining ［J］. Knowledge-Based Systems， 2020， 196： 105812.

[23] WANG L Z， BAO X G， ZHOU L H. Redundancy reduction for prevalent co-location patterns ［J］. IEEE Transactions on Knowledge and Data Engineering， 2018， 30（1）： 142-155.

[24] 王晓璇，王丽珍，陈红梅，等. 基于特征效用参与率的空间高效用co-location模式挖掘方法［J］. 计算机学报， 2019， 42（8）： 1721-1738.（WANG X X， WANG L Z， CHEN H M， et al. Mining spatial high utility co-location patterns based on feature utility ratio ［J］. Chinese Journal of Computers， 2019， 42（8）： 1721-1738.）

[25] 马董，陈红梅，王丽珍，等. 空间亚频繁co-location模式的主导特征挖掘［J］. 计算机应用， 2020， 40（2）： 465-472.（MA D， CHEN H M， WANG L Z， et al. Dominant feature mining of spatial sub-prevalent co-location patterns ［J］. Journal of Computer Applications， 2020， 40（2）： 465-472.）

[26] LIU C H， GUO C H. Mining top-N high-utility operation patterns for taxi drivers ［J］. Expert Systems with Applications， 2021， 170： 114546.

[27] WU Y X， GENG M， LI Y， et al. HANP-Miner： high average utility nonoverlapping sequential pattern mining ［J］. Knowledge-Based Systems， 2021， 229： 107361.

[28] GAN W S， LIN J C， FOURNIER-VIGER P， et al. HUOPM： high-utility occupancy pattern mining ［J］. IEEE Transactions on Cybernetics， 2020， 50（3）： 1195-1208.

[29] WU Y X， CHEN M J， LI Y， et al. ONP-Miner： one-off negative sequential pattern mining ［EB/OL］. ［2022-07-25］. https：//arxiv.org/pdf/2207.11950.pdf.

[30] DONG X J， GONG Y S， CAO L B. e-RNSP： an efficient method for mining repetition negative sequential patterns ［J］. IEEE Transactions on Cybernetics， 2020， 50（5）： 2084-2096.

[31] WU Y X， LUO L F， LI Y， et al. NTP-Miner： nonoverlapping three-way sequential pattern mining ［J］. ACM Transaction on Knowledge Discovery from Data， 2022， 16（3）： 51.

[32] JI X N， BAILEY J， DONG G Z. Mining minimal distinguishing subsequence patterns with gap constraints ［J］. Knowledge and Information Systems， 2007， 11（3）： 259-286.

[33] WANG X M， DUAN L， DONG G Z， et al. Efficient mining of density-aware distinguishing sequential patterns with gap constraints ［J］. Database Systems for Advanced Applications， 2014， 8421： 372-387.

[34] 段磊，唐常杰，杨宁，等. 基于显露模式的对比挖掘研究及应用进展［J］. 计算机应用， 2012， 32（2）：304-308.（DUAN L， TANG C J， YANG N， et al. Survey on emerging pattern based contrast mining and applications ［J］. Journal of Computer Applications， 2012， 32（2）： 304-308.）

[35] WU Y X， WANG Y H， LIU J Y， et al. Mining distinguishing subsequence patterns with nonoverlapping condition ［J］. Cluster Computing， 2019， 22： 5905-5907.

[36] HE Z Y， ZHANG S M， GU F Y， et al. Mining conditional discriminative sequential patterns ［J］. Information Sciences， 2019， 478： 524-539.

[37] 武优西，户倩，郭媛，等.保序序列模式挖掘方法： CN202010544303.5 ［P］. 2020-06-15.（WU Y X， H Q， GUO Y， et al. Order-preserving sequential pattern mining algorithm： CN202010544303.5 ［P］. 2020-06-15.）

[38] 武优西，赵晓倩，李艳，等.保序序列规则挖掘方法： CN202210294476.5 ［P］. 2022-03-23.（WU Y X， ZHAO X Q， LI Y， et al. Order-preserving sequential rule mining algorithm： CN202210294476.5 ［P］. 2022-03-23.）

[39] 武优西，刘锦，耿萌，等.近似保序序列模式挖掘方法： CN202210295950.6 ［P］. 2022-03-23.（WU Y X， LIU J， GENG M， et al. Approximate order-preserving sequential pattern mining algorithm： CN202210295950.6 ［P］. 2022-03-23.）

Contrast order-preserving pattern mining algorithm

MENG Yufei1， WU Youxi1*， WANG Zhen1， LI Yan2

（1，，300401，；2，，300401，）

Aiming at the problem that the existing contrast sequential pattern mining methods mainly focus on character sequence datasets and are difficult to be applied to time series datasets， a new Contrast Order-preserving Pattern Mining （COPM） algorithm was proposed. Firstly， in the candidate pattern generation stage， a pattern fusion strategy was used to reduce the number of candidate patterns. Then， in the pattern support calculation stage， the support of super-pattern was calculated by using the matching results of sub-patterns. Finally， a dynamic pruning strategy of minimum support threshold was designed to further effectively prune the candidate patterns. Experimental results show that on six real time series datasets， the memory consumption of COPM algorithm is at least 52.1% lower than that of COPM-o （COPM-original） algorithm， 36.8% lower than that of COPM-e （COPM-enumeration） algorithm， and 63.6% lower than that of COPM-p （COPM-prune） algorithm. At the same time， the running time of COPM algorithm is at least 30.3% lower than that of COPM-o algorithm， 8.8% lower than that of COPM-e algorithm and 41.2% lower than that of COPM-p algorithm. Therefore， in terms of algorithm performance， COPM algorithm is superior to COPM-o， COPM-e and COPM-p algorithms. The experimental results verify that COPM algorithm can effectively mine the contrast order-preserving patterns to find the differences between different classes of time series datasets.

pattern mining; sequential pattern mining; time series; contrast pattern; order-preserving pattern

This work is partially supported by Natural Science Foundation of Hebei Province （F20202013）.

MENG Yufei， born in 1995， M. S. candidate. Her research interests include data mining.

WU Youxi， born in 1974， Ph. D.， professor. His research interests include data mining， machine learning.

WANG Zhen， born in 1997， M. S. candidate. Her research interests include data mining.

LI Yan， born in 1975， Ph. D.， associate professor. Her research interests include data mining， supply chain management.

TP311.13

A

1001-9081（2023）12-3740-07

10.11772/j.issn.1001-9081.2022121828

2022⁃12⁃09；

2023⁃02⁃24；

2023⁃02⁃28。

河北省自然科学基金资助项目（F2020202013）。

孟玉飞（1995—），女，河北石家庄人，硕士研究生，主要研究方向：数据挖掘；武优西（1974—），男，天津人，教授，博士，CCF杰出会员，主要研究方向：数据挖掘、机器学习；王珍（1997—），女，河南周口人，硕士研究生，主要研究方向：数据挖掘；李艳（1975—），女，天津人，副教授，博士，主要研究方向：数据挖掘、供应链管理。