L1正则化的深度谱聚类算法
李文博,刘波*,陶玲玲,罗棻,张航
L1正则化的深度谱聚类算法
李文博1,2,刘波1,2*,陶玲玲1,2,罗棻1,2,张航1,2
(1.重庆工商大学 人工智能学院,重庆 400067; 2.智能感知与区块链技术重庆市重点实验室(重庆工商大学),重庆 400067)(∗通信作者电子邮箱liubo7971@163.com)
针对深度谱聚类模型训练不稳定和泛化能力弱等问题,提出L1正则化的深度谱聚类算法(DSCLR)。首先,在深度谱聚类的目标函数中引入L1正则化,使深度神经网络模型生成的拉普拉斯矩阵的特征向量稀疏化,并提升模型的泛化能力;其次,通过利用参数化修正线性单元激活函数(PReLU)改进基于深度神经网络的谱聚类算法的网络结构,解决模型训练不稳定和欠拟合问题。在MNIST数据集上的实验结果表明,所提算法在聚类精度(CA)、归一化互信息(NMI)指数和调整兰德系数(ARI)这3个评价指标上,相较于深度谱聚类算法分别提升了11.85、7.75和17.19个百分点。此外,所提算法相较于深度嵌入聚类(DEC)和基于对偶自编码器网络的深度谱聚类(DSCDAN)等算法,在CA、NMI和ARI这3个评价指标上也有大幅提升。
深度聚类;谱聚类;L1正则化;深度学习;无监督学习
0 引言
计算机技术的广泛应用产生了海量的数据[1],如视频数据、音频数据和文本数据等,而这些数据大多数都没有标记。如何处理这些无标记数据是目前机器学习面临的巨大挑战之一。聚类是无监督机器学习领域中最重要的方法。聚类通过某种度量方法将相似的数据分配到同一个聚簇,不相似的数据分配到其他聚簇[2]。
目前,聚类已经被广泛应用于航路发现[3]、医学图像分析[4]、缺陷检测[5]和左右轨道线检测[6]等。聚类方法大致分为两类:1)传统的聚类方法。利用经典的机器学习理论进行研究,如基于分区的均值聚类(-means clustering,-means)[7]、谱聚类(Spectral Clustering,SC)[8]、基于层次的凝聚聚类(analysis of Agglomerative Clustering,AC)[9]和具有噪声的基于密度的聚类方法DBSCAN(Density-Based Spatial Clustering of Applications with Noise)[10]等。2)深度聚类方法。这类方法利用深度神经网络理论进行研究,如利用自编码器实现聚类[11],将深度学习与-means结合提升聚类性能[12]和将深度神经网络与谱聚类结合的方法[13-14]等。相较于传统聚类算法,深度聚类算法性能良好,但仍旧面临很多问题,例如聚类结果不稳定和泛化性能差等问题。
针对上述问题,本文提出L1正则化的深度谱聚类算法(Deep Spectral Clustering algorithm with L1 Regularization,DSCLR)。首先,在深度谱聚类算法SpectralNet(Spectral Clustering using Deep Neural Network)算法[13]损失函数中加入L1正则化使拉普拉斯矩阵的特征向量稀疏化,从而增强模型的鲁棒性和泛化性;其次,针对SpectralNet网络结构容易过拟合的问题,将神经网络模型的激活函数修改为参数化修正线性单元激活函数(Parametric Rectified Linear Unit, PReLU)[15],使得深度神经网络模型训练更稳定;最后,在多个数据集上利用聚类评价指标与基准方法对实验结果进行对比分析和可视化,验证了所提算法的有效性。
1 相关工作
1.1 深度聚类
聚类是目前机器学习、数据挖掘领域研究的主要方法之一。基于划分[7-8]、层次[9]和密度[10]聚类等传统聚类方法虽然应用广泛,但在聚类高维复杂的大规模数据时,性能都较差。近年,深度神经网络因具有强大的表示学习能力而被应用到各个领域。深度学习与聚类结合(即深度聚类)使聚类性能大幅提升,如文献[11-12]中使用自编码器作为特征学习模块,并通过同时最小化自编码器和-means的损失函数实现聚类。文献[13]中提出通过深度神经网络模型获得拉普拉斯矩阵的特征向量,并称这种算法为SpectralNet;虽然这种模型简单有效,但训练过程不稳定、模型泛化性差。文献[14]中利用对偶自编码器模型生成具体判断性和鲁棒性的特征,并将这些特征作为深度谱聚类模型的输入,从而构建更稳定的拉普拉斯矩阵。与之类似,文献[16]中提出了一种基于卷积神经网络的谱聚类算法,通过利用预训练卷积神经网络提取图像边缘并进行特征融合,以减轻算法对相似矩阵的依赖。文献[17]中结合谱聚类、生成对抗网络和贝叶斯框架,通过低秩模型估计聚类数,用谱聚类获取隐藏空间结构,在此基础上利用对抗学习完成聚类。这些模型的聚类效果通常较好,但它们的结构非常复杂,较难训练。文献[18-19]中结合自编码器与子空间聚类提高样本的非线性表达,以提升聚类效果。这类方法对噪声较敏感且无法很好地表示样本之间的关系。文献[20]中提出将SpectralNet扩展到多视图场景,每个视图都用一个SpectralNet进行深度聚类;这种方法的缺点是计算量较大。文献[21]中提出一种解决谱聚类局限的图聚类方法,通过制定归一化最小切问题的连续松弛并通过训练图神经网络使得该目标最小化;但是该方法无法得到高阶的连通性,并且经常无法恢复聚簇的结构。
1.2 L1正则化
特征选择相关研究最先引入L1正则化,具体地,在特征选择的损失函数中添加L1范数,让学习到的模型具有稀疏解,以提高特征选择的可解释性[22]。文献[23]中提出一种在回归系数的绝对值之和小于一个常数的约束条件下,使残差平方和最小化从而产生某些严格等于零的回归系数,最后得到更具可解释性的模型。文献[24]中提出L1正则化的支持向量机(Support Vector Machine, SVM)聚类算法,实现了同时聚类和特征选择功能。文献[25]中提出了一种约束的谱聚类算法,通过引入L1正则化使模型具有稀疏性。文献[26]中提出了一种具用全局特征选择的神经模型,将L1正则化线性回归的特征引入深度神经网络模型,以实现深度神经网络模型稀疏化。文献[27]中提出了一种L1正则化对称非负矩阵因子分解算法,解决高阶协同聚类(High-Order Co-Clustering, HOCC)问题。文献[28]中通过引入L1正则化减少噪声,使模型更具鲁棒性。文献[29]中设计了一种平滑优化算法求解基于L1正则化的聚类目标函数,能够得到较好的近似解。综上所述,基于L1正则化的模型受到了广泛的研究并取得了较好的应用。
2 DSCLR
2.1 SpectralNet算法
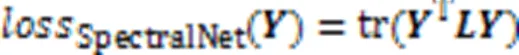
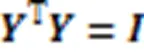
研究表明,SpectralNet在聚类时容易出现结果不稳定和泛化性差等问题。为了解决此类问题,本文提出了DSCLR。
2.2 本文算法的模型结构
DSCLR的模型整体框架主要由自编码器模块、正交模块和特征映射(Feature Map)模块这3个模块组成,如图1所示。由于正交模块和特征映射模块是共用网络结构,因此在图1中正交和特征映射模块对应一个网络结构。
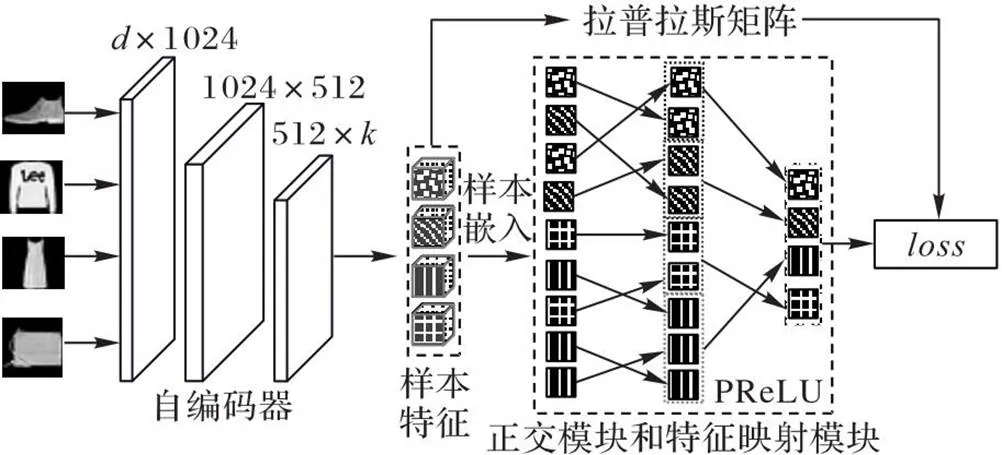
图1 DSCLR的模型整体框架
图1中的自编码器模块用于从样本中提取特征,然后利用这些特征构造拉普拉斯矩阵;正交模块用于保证学习到的特征向量的正交性;特征映射模块用于学习如何将样本构成拉普拉斯矩阵的特征向量。
此外,为了得到聚类结果更稳定和拟合能力更好的模型,本文通过将深度神经网络模型的激活函数改为PReLU激活函数[15]在几乎不增加额外参数的前提下提升模型训练的稳定性并减少模型的过拟合。具体各模块详细网络结构设计如表1所示。
表1DSCLR的网络结构
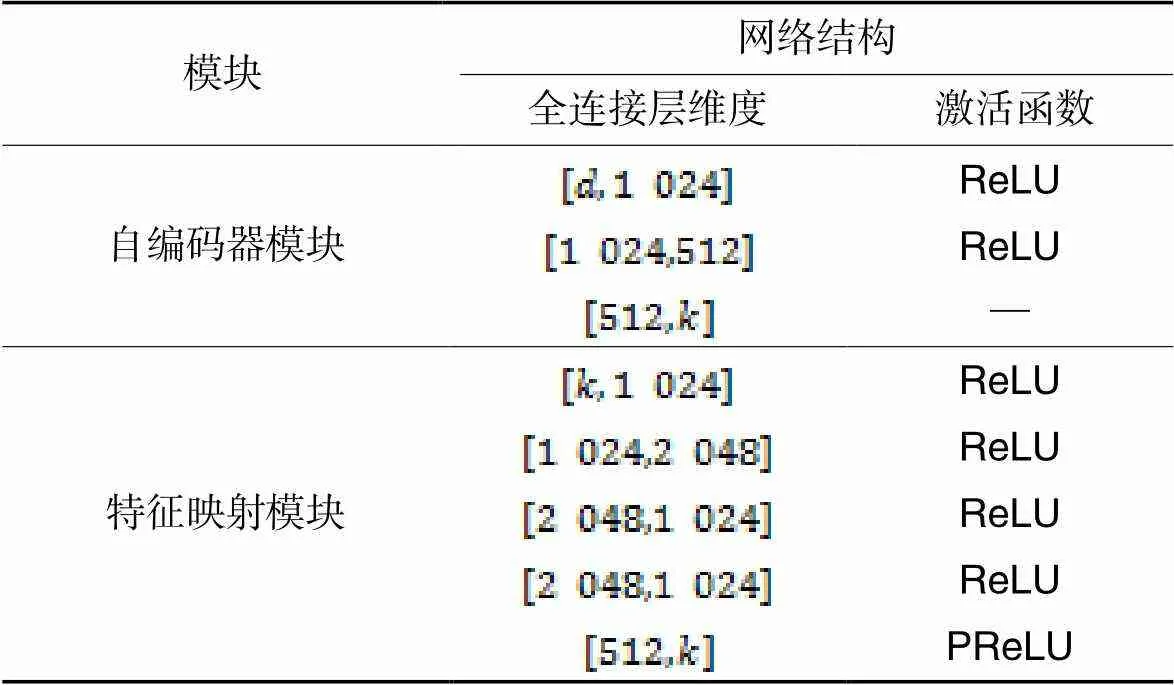
Tab.1 Network architecture of DSCLR
2.3 DSCLR
为了提高本文算法模型的稳定性和泛化能力,进一步在式(1)中引入L1正则化,从而得到如下的损失函数:
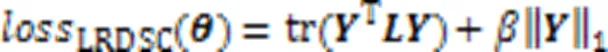
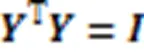
算法1 L1正则化的深度谱聚类算法。
5)重复执行步骤3)~6),直到算法收敛;
3 实验与结果分析
3.1 实验设置
3.1.1基准数据集
表2汇总了本实验所用到的数据集的基本信息。

图2 COIL20数据集的部分图像
表2数据集详情
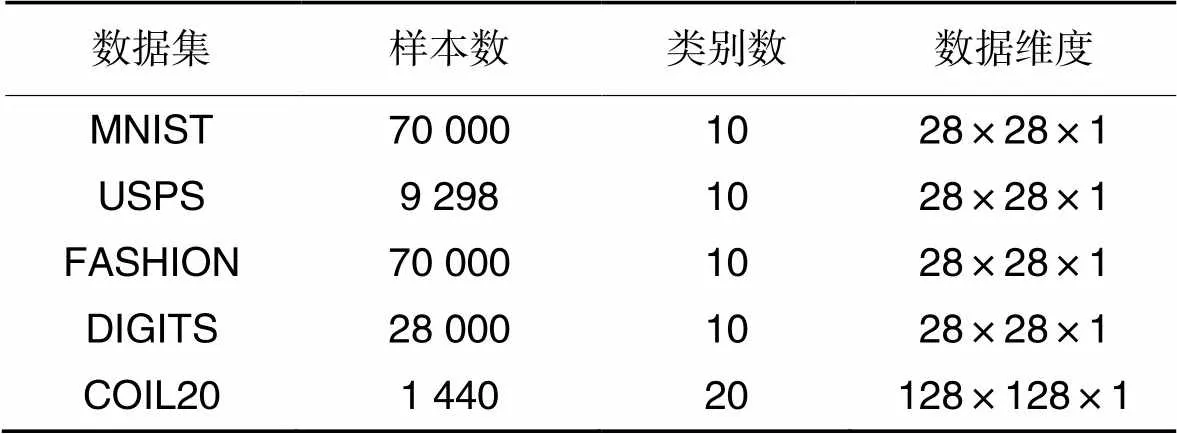
Tab.2 Dataset details
3.1.2基准算法
将本文算法分别与以下6种具有代表性的传统聚类算法和深度聚类算法进行比较。

2)AC算法[9]使用自下而上的方法进行层次聚类,最初每一个样本都被认为是一个聚簇,然后根据度量策略合并这些聚簇,最后完成聚类。
3)DBSCAN算法[10]是一种基于密度的聚类算法,它将聚簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为聚簇。
4)SC算法[8]是一种谱聚类算法。通过将样本看作空间中的点,用边连接这些点并给每条边定义一个权值,权值大小与样本之间的距离相关,距离较近的两个样本权值高,反之则低,从而构成了无向加权图,然后通过对图的划分实现聚类。
5)DEC(Deep Embedding Clustering)算法[11]通过学习数据到潜空间的映射,然后通过优化目标对潜空间数据进行聚类。
6)SpectralNet算法[13]通过深度神经网络显式学习样本与拉普拉斯特征向量之间的映射,然后用-means对这些特征向量进行聚类。
7)基于对偶自编码器网络的深度谱聚类(Deep Spectral Clustering using Dual Autoencoder Network,DSCDAN)算法[14]首先通过设计双自动编码器网络,对潜在表示及其噪声版本施加重构约束,将输入嵌入潜在空间进行聚类,其次利用互信息估计,从输入中提取更多的鉴别信息,最后采用深度谱聚类方法将潜在表示嵌入特征空间,并对它进行聚类。
8)深度嵌入谱聚类(Spectral Clustering with Deep Embedding, SCDE)算法[35]通过学习一个自编码器估计聚簇的类别数并对它进行聚类。
3.1.3评价指标
为了评估聚类的效果,本文采用了3种常用的聚类评价指标,分别是聚类准确率(Clustering Accuracy, CA)[36]、归一化互信息(Normalized Mutual Information, NMI)指数[37]和调整兰德系数(Adjusted Rand Index, ARI)[38]。
3.1.4实验环境与参数设置
1)实验环境。
本文实验在以下环境进行:Intel Xeon Platinum 8358 CPU@2.60 GB处理器、NVIDIA Corporation A100 80 GB显卡,Ubuntu 18.04.1 LTS操作系统,PyTorch 1.10.0,Python 3.7.12。
2)参数设置。
3.2 实验结果
为了验证本文算法的有效性,在5个真实数据集上分别通过CA、NMI和ARI这3个聚类评价指标比较DSCLR与其他聚类算法的性能。在实验中通过随机将基准数据集按照8∶2划分为训练集和测试集进行训练以评估所有算法的性能。
3.2.1聚类结果分析
由表3的CA评价指标可知,本文算法在MNIST、DIGISTS和FASHION数据集的聚类精度获得最好的结果。在5个实验数据集上,相较于SpectralNet,本文算法的CA分别提高了11.85、6.86、2.44、18.97和7.47个百分点;此外,在MNIST、DIGITS和COIL20这3个数据集上,本文算法的CA相较于DEC分别提高了1.20、12.57和8.44个百分点,相较于DSCDAN分别提升了8.00、5.57和21.84个百分点。
由表3的NMI评价指标可知,本文算法在DIGISTS、USPS、COIL20和FASHION数据集上的NMI指数获得了最好结果,在MNIST数据集上仅比最优的DEC低1.68个百分点。在5个实验数据集上,相较于SpectralNet,本文算法的NMI分别提高了7.75、0.59、0.74、23.31和0.76个百分点。在MNIST、DIGITS和COIL20这3个数据集上,相较于DEC和DSCDAN,本文算法同样展现了显著的提升。
由表3的ARI评价指标可知,本文算法在DIGISTS和COIL20数据集上的ARI达到了最好结果,在USPS数据集上仅比DEC低2.24个百分点。在MNIST、DIGITS和COIL20这3个实验数据集上,相较于SpectralNet,本文算法的ARI分别提高了17.19、4.66、12.05百分点;相较于DEC,本文算法的ARI分别提高了1.32、10.8和5.93个百分点。
综上所述,本文算法具有更好的聚类性能。其中在对比的基准数据集上本文算法明显优于SpectralNet、DEC和DSCDA等深度聚类算法,这也验证了L1正则化和PReLU激活函数对拉普拉斯特征稀疏化和模型训练的稳定性起到了重要的作用。
表3各算法在不同数据集上的CA、NMI和ARI值 单位:%
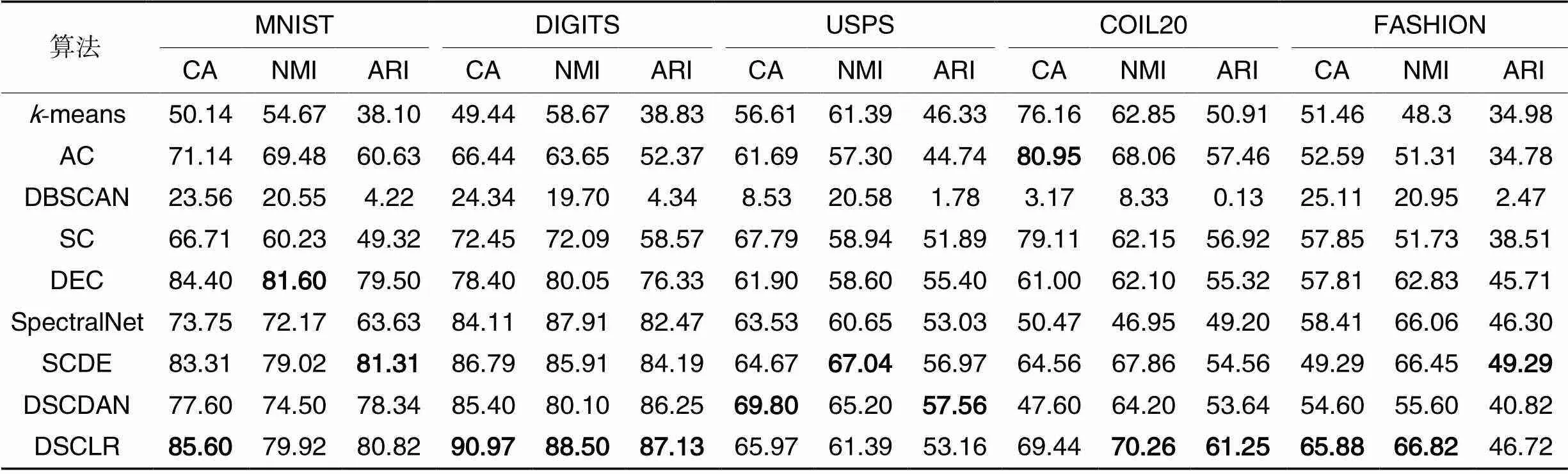
Tab.3 CA,NMI and ARI values of different algorithms on different datasets unit:%
注:加粗数据为最优结果。
3.2.2T-SNE可视化分析
本文针对MNIST数据集利用t分布随机邻域嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)算法[38]分别对原始数据、自编码器提取特征之后的数据、表3的SpectralNet算法的拉普拉斯矩阵数据和本文算法的拉普拉斯特征矩阵数据进行降维可视化操作。可视化结果如图3所示。
图3(a)为MNIST原始数据的可视化结果,图3(b)为自编编码器对MNIST提取特征之后的可视化结果,图3(c)为SpectralNet聚类结果的可视化,图3(d)为本文算法对MNIST数据集的可视化结果。从图3可以看出,本文算法的聚类效果最优。具体地,SpectralNet明显有3个聚簇边缘是混合在一起的,本文算法聚簇之间都能较好地分开。
综上所述,本文算法能够通过深度神经网络模型计算更稀疏的拉普拉斯矩阵的特征向量,稀疏的特征向量在聚类时表现了更好的鲁棒性,从而得到更好的聚类结果。
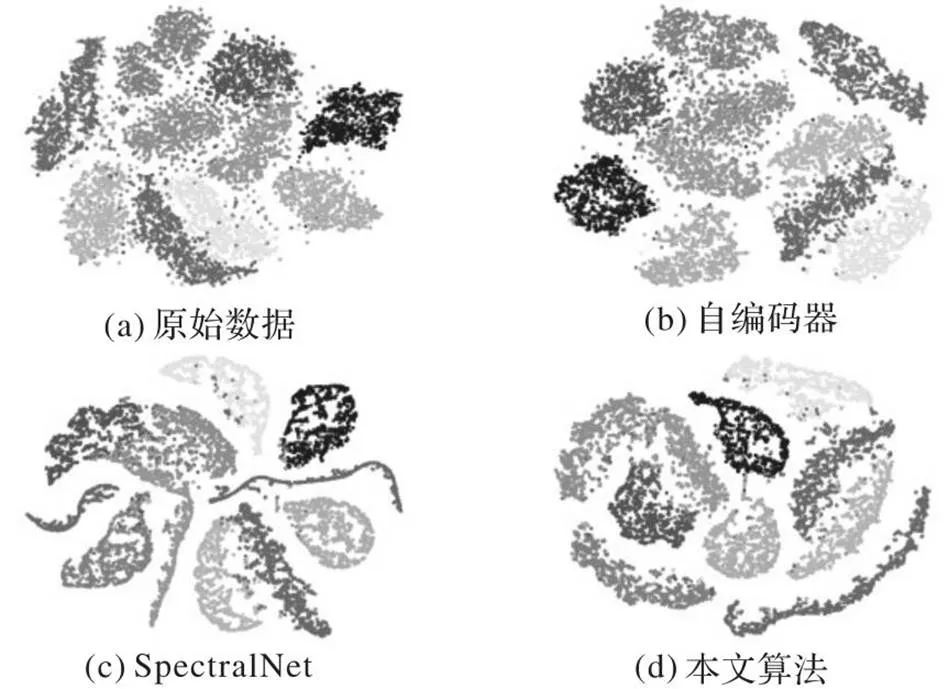
图3 MNIST数据集的t-SNE可视化结果
3.3 超参数分析实验
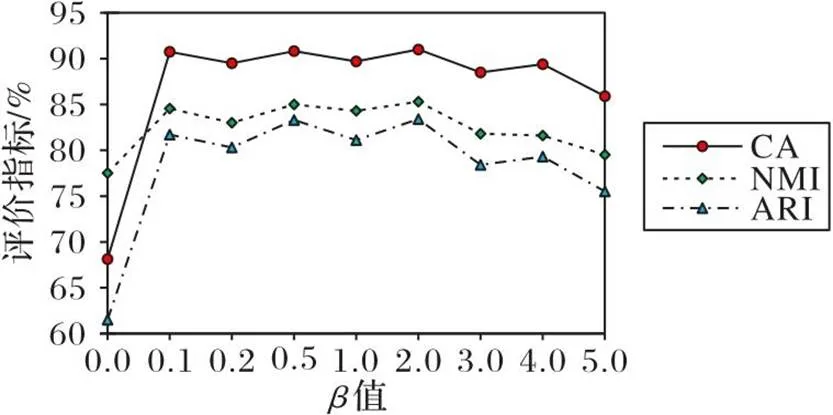
图4 MNIST数据集上不同的值对评价指标的影响
3.4 L1正则化与PReLU激活函数消融实验
由图5可知,采用PReLU激活函数策略的模型在聚类精度和训练稳定性上显著优于其他策略;未采用L1正则化算法的模型在聚类精度上明显不如采用L1正则化的策略。
以上实验结果充分验证了L1正则化和PReLU对本文算法的有效性。
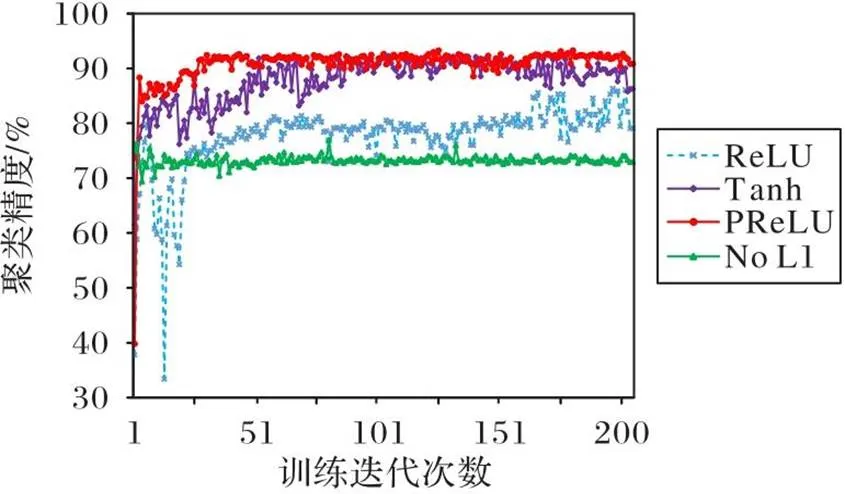
图5 不同训练策略对算法性能的影响
4 结语
本文提出了一种L1正则化的深度谱聚类算法,该算法通过L1正则化使学习到的拉普拉斯矩阵的特征向量稀疏化,通过调整深度谱聚类网络结构和激活函数,使所提算法具有更好的泛化能力和更加稳定的聚类性能。今后的工作中,将进一步设计新的目标函数,强化特征向量的稀疏性,从而提升深度谱聚类的性能;同时考虑针对不同模态的数据引入新的网络结构改进深度谱聚类模型。
[1] GUO X, LIU X, ZHU E, et al. Adaptive self-paced deep clustering with data augmentation[J]. IEEE Transactions on Knowledge and Data Engineering, 2019, 32(9): 1680-1693.
[2] JAIN A K, MURTY M N, FLYNN P J. Data clustering: a review[J]. ACM Computing Surveys (CSUR), 1999, 31(3): 264-323.
[3] 刘海杨,孟令航,林仲航,等.基于轨迹点聚类的航路发现方法[J]. 计算机应用, 2022, 42(3): 890-894.(LIU H Y, MENG L H, LIN Z H, et al. GU. Route discovery method based on trajectory point clustering[J]. Journal of Computer Applications, 2022, 42(3): 890-894.)
[4] 祝承,赵晓琦,赵丽萍,等. 基于谱聚类半监督特征选择的功能磁共振成像数据分类[J]. 计算机应用, 2021, 41(8): 2288-2293.(ZHU C, ZHAO X Q, ZHAO L P, et al. Classification of functional magnetic resonance imaging data based on semi-supervised feature selection by spectral clustering[J]. Journal of Computer Applications, 2021, 41(8): 2288-2293.)
[5] 袁野,谭晓阳. 复杂环境下的冰箱金属表面缺陷检测[J]. 计算机应用, 2021, 41(1): 270-274.(YUAN Y, TAN X Y. Defect detection of refrigerator metal surface in complex environment[J]. Journal of Computer Applications, 2021, 41(1): 270-274.)
[6] 曾祥银,郑伯川,刘丹. 基于深度卷积神经网络和聚类的左右轨道线检测[J]. 计算机应用, 2021, 41(8): 2324-2329.(ZENG X Y, ZHENG B C, LIU D. Detection of left and right railway tracks based on deep convolutional neural network and clustering[J]. Journal of Computer Applications, 2021, 41(8): 2324-2329.)
[7] KANUNGO T, MOUNT D M, NETANYAHU N S, et al. An efficient-means clustering algorithm: analysis and implementation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(7): 881-892.
[8] VON L U. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17(4): 395-416.
[9] ACKERMANN M R, BLÖMER J, KUNTZE D, et al. Analysis of agglomerative clustering[J]. Algorithmica, 2014, 69(1): 184-215.
[10] ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise [EB/OL]. [2022-10-20]. https://cdn.aaai.org/KDD/1996/KDD96-037.pdf.
[11] XIE J, GIRSHICK R, FARHADI A. Unsupervised deep embedding for clustering analysis[C]// Proceedings of the 33th International Conference on Machine Learning. [S.l.]: PMLR, 2016: 478-487.
[12] YANG B, FU X, SIDIROPOULOS N D, et al. Towards K-means-friendly spaces: simultaneous deep learning and clustering[C]// Proceedings of the 34th International Conference on Machine Learning. [S.l.]: PMLR, 2017: 3861-3870.
[13] SHAHAM U, STANTON K, LI H, et al. SpectralNet: spectral clustering using deep neural networks [C]// Proceedings of the 6th International Conference on Learning Representations. Vancouver: OpenReview.net, 2018, 1050: 10.
[14] YANG X, DENG C, ZHENG F, et al. Deep spectral clustering using dual autoencoder network[C]// Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2019: 4066-4075.
[15] HE K, ZHANG X, REN S, et al. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification [C]// Proceedings of the 2015 IEEE/CVF International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2015: 1026-1034.
[16] 苏常保,龚世才.一种基于卷积神经网络的谱聚类算法[J].安徽大学学报(自然科学版),2022,46(5):20-26.(SU C B, GONG S C. A spectral clustering algorithm based on convolutional neural network[J]. Journal of Anhui University(Natural Sciences), 2022,46(5):20-26.)
[17] YE X, ZHAO J, CHEN Y, et al. Bayesian adversarial spectral clustering with unknown cluster number [J]. IEEE Transactions on Image Processing, 2020, 29: 8506-8518.
[18] JI P,ZHANG T,LI H,et al.Deep subspace clustering networks[C]// Proceedings of the 30th Advances in Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017:24-33.
[19] ZHOU L,WANG S,BAI X,et al.Iterative deep subspace clustering[C]// Proceedings of the 2018 Joint IAPR International Workshop Structural,Syntactic,and Statistical Pattern Recognition. Cham: Springer, 2018:42-51.
[20] HUANG S, OTA K, DONG M, et al. MultiSpectralNet: spectral clustering using deep neural network for multi-view data[J]. IEEE Transactions on Computational Social Systems, 2019, 6(4): 749-760.
[21] BIANCHIF M, GRATTAROLA D, ALIPPI C. Spectral clustering with graph neural networks for graph pooling [C]// Proceedings of the 37th International Conference on Machine Learning. [S.l.]: PMLR, 2020: 874-883.
[22] TIBSHIRANI R. Regression shrinkage and selection via the lasso: a retrospective[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2011, 73(3): 273-282.
[23] TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1996, 58(1): 267-288.
[24] 刘建伟,李双成,付捷,等.L1范数正则化SVM聚类算法[J].计算机工程,2012,38(12):185-187.(LIU J W, LI S C, FU J, et al. L1-norm regularized SVM clustering algorithm[J]. Computer Engineering, 2012,38(12):185-187.)
[25] KAWALE J, BOLEY D. Constrained spectral clustering using L1 regularization[C]// Proceedings of the 2013 SIAM International Conference on Data Mining. Philadelphia,PA: SIAM, 2013: 103-111.
[26] LEMHADRI I, RUAN F, TIBSHIRANI R. LassoNet: neural networks with feature sparsity[C]// Proceedings of the 24th International Conference on Artificial Intelligence and Statistics. [S.l.]: PMLR, 2021: 10-18.
[27] LIU K, WANG H. High-order co-clustering via strictly orthogonal and symmetric L1-norm nonnegative matrix tri-factorization[C]//Proceedings of the 27th International Joint Conference on Artificial Intelligence. Menlo Park, CA: AAAI Press , 2018: 2454-2460.
[28] ZHAO M, LIU J. Robust clustering with sparse corruption via ℓ2, 1, ℓ1 norm constraint and Laplacian regularization[J]. Expert Systems with Applications, 2021, 186: 115704.
[29] BAGIROV A M, MOHEBI E. An algorithm for clustering using L1-norm based on hyperbolic smoothing technique[J]. Computational Intelligence, 2016, 32(3): 439-457.
[30] DENG L. The MNIST database of handwritten digit images for machine learning research [J]. IEEE Signal Processing Magazine, 2012, 29(6):141-142..
[31] HULL J J. A database for handwritten text recognition research[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(5): 550-554.
[32] COHEN G, AFSHAR S, TAPSON J, et al. EMNIST: extending MNIST to handwritten letters[C]// Proceedings of the 13th International Joint Conference on Neural Networks. Piscataway: IEEE, 2017: 2921-2926.
[33] XIAO H, RASUL K, VOLLGRAF R. Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms [EB/OL]. [2022-10-20]. https://arxiv.org/pdf/1708.07747v1.pdf.
[34] NENE S A. Columbia object image library [DB/OL]. [2022-10-20]. https://www1.cs.columbia.edu/CAVE/publications/pdfs/Nene_TR96.pdf.
[35] DUAN L, MA S, AGGARWAL C, et al. Improving spectral clustering with deep embedding, cluster estimation and metric learning[J]. Knowledge and Information Systems, 2021, 63(3): 675-694.
[36] CAI D, HE X, HAN J. Locally consistent concept factorization for document clustering[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 23(6): 902-913.
[37] VINH N, EPPS J, BAILEY J. Information theoretic measures for clusterings comparison: is a correction for chance necessary?[C]//Proceedings of the 26th Annual International Conference on Machine Learning. New York: ACM, 2009: 1073-1080.
[38] VAN DER MAATEN L, HINTON G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(11): 2579-2605.
Deep spectral clustering algorithm with L1 regularization
LI Wenbo1,2, LIU Bo1,2*, TAO Lingling1,2, LUO Fen1,2, ZHANG Hang1,2
(1,,400067,;2(),400067,)
Aiming at the problems that the deep spectral clustering models perform poorly in training stability and generalization capability, a Deep Spectral Clustering algorithm with L1 Regularization (DSCLR) was proposed. Firstly, L1 regularization was introduced into the objective function of deep spectral clustering to sparsify the eigen vectors of the Laplacian matrix generated by the deep neural network model. And the generalization capability of the model was enhanced. Secondly, the network structure of the spectral clustering algorithm based on deep neural network was improved by using the Parametric Rectified Linear Unit activation function (PReLU) to solve the problems of model training instability and underfitting. Experimental results on MNIST dataset show that the proposed algorithm improves Clustering Accuracy (CA), Normalized Mutual Information (NMI) index, and Adjusted Rand Index (ARI) by 11.85, 7.75, and 17.19 percentage points compared to the deep spectral clustering algorithm, respectively. Furthermore, the proposed algorithm also significantly improves the three evaluation metrics, CA, NMI and ARI, compared to algorithms such as Deep Embedded Clustering (DEC) and Deep Spectral Clustering using Dual Autoencoder Network (DSCDAN).
deep clustering; spectral clustering; L1 regularization; deep learning; unsupervised learning
This work is partially supported by Science and Technology Research Program of Chongqing Municipal Education Commission (KJZD-K202200803), Chongqing Natural Science Foundation (cstc2018jcyjAX0057), Graduate Innovative Scientific Research Project of Chongqing Technology and Business University (yjscxx2022-112-68).
LI Wenbo, born in 1998, M. S. candidate. His research interests include deep clustering, unsupervised learning, computer vision.
LIU Bo, born in 1977, Ph. D., associate professor. His research interests include graph neural network, generative adversarial network, interpretability of deep learning, video analysis and understanding.
TAO Lingling, born in 1998, M. S. candidate. Her research interests include computer vision, image processing, generative adversarial network.
LUO Fen, born in 1975, M. S.,lecturer. His research interests include computer vision, medical image processing.
ZHANG Hang, born in 1998, M. S. candidate. His research interests include machine learning, computer vision, deep clustering.
TP311.5
A
1001-9081(2023)12-3662-06
10.11772/j.issn.1001-9081.2022121822
2022⁃12⁃06;
2023⁃02⁃20;
2023⁃02⁃27。
重庆市教委科学技术研究项目(KJZD⁃K202200803);重庆市自然科学基金资助项目(cstc2018jcyjAX0057);重庆工商大学研究生“创新型科研项目”(yjscxx2022⁃112⁃68)。
李文博(1998—),男,重庆人,硕士研究生,主要研究方向:深度聚类、无监督学习、计算机视觉;刘波(1977—),男,重庆人,副教授,博士,主要研究方向:图神经网络、生成对抗网络、深度学习的可解释性、视频分析与理解;陶玲玲(1998—),女,重庆人,硕士研究生,主要研究方向:计算机视觉、图像处理、生成对抗网络;罗棻(1975—),男,重庆人,讲师,硕士,主要研究方向:计算机视觉、医学图像处理;张航(1998—),男,重庆人,硕士研究生,主要研究方向:机器学习、计算机视觉、深度聚类。

