拉索方法对脉冲折流板萃取柱存留分数的预测
金磊, 高杨, 何辉,2, 谢滨骏龙, 周羽, 张萌
(1.哈尔滨工程大学 核科学与技术学院,黑龙江 哈尔滨 150001; 2.中国原子能科学研究院, 北京 102413)
液液萃取是乏燃料后处理过程中常见的一种操作,通常是在脉冲萃取柱混合澄清槽等萃取设备中进行。为了增加两相的对流强度,增大两相接触面积,学者对萃取柱进行了改进,提出了多种类型的改进的萃取柱[1]:脉冲筛板柱[2-3];脉冲折流板柱[4-6];转盘柱[7-8]以及钻孔转盘柱[9]等。这些萃取柱广泛的应用于乏燃料后处理、生物工程和湿法冶金等领域中[10-12]。其中脉冲折流板萃取柱由于其高通量,结构简单,没有内部运动组件等优点,在核燃料领域得到大量的关注和研究[13-14]。为了能够更好地完成脉冲折流板萃取柱的设计和改进,了解脉冲折流板萃取柱中各个操作参数的影响尤为重要。相关学者对萃取柱中的水力学参数如存留分数、液滴大小[15]、液滴速度和特征速度等[16-20]都做了大量的分析和研究,并提出了在不同操作区间内的相关水力学参数随着操作参数变化的预测方程。
关于存留分数的预测方程为重点,不少水力学参数的预测方程都与存留分数的变化相关。然而,这些存留分数预测方程中包含了过多的高次项函数的乘积,使其适用范围非常狭窄,在其他数据集上预测结果和实际值偏差过大,并且难以确定在存留分数变化中起主导作用的操作参数。随着计算机的不断发展,越来越多的数据分析方法被成功应用到工业生产当中[21-22]。拉索回归(the least absolute shrinkage and selection operator, LASSO)方法是一种L1正则化回归[23],该方法能够有效地平衡从数据中回归分析出的非线性方程的复杂性和准确性。并且能够使一些参数前的系数收敛到0,从而对待选的高次项函数做出有效的筛选,避免过度拟合。
本文主要使用LASSO方法从实验数据中回归分析出关于脉冲折流板萃取柱中存留分数随着分散相速度,连续相速度和脉冲强度变化的多元二次型预测方程。同时将LASSO方法与其他经验关联式进行对比分析拟合方程的预测值和实验值的相对误差(mean relative error,MRE),并根据预测方程分析相关操作参数对存留分数的影响大小。本文为脉冲折流板萃取柱中分散相液滴粒径分布,分散相液滴速度分布等水力学参数的研究提供分析方法,并为萃取柱设计和操作参数的选取提供理论数据支撑。
1 存留分数测试与预测方程拟合方法
1.1 实验设备
实验所使用的脉冲折流板萃取柱如图1所示。

注:1.水相入口,2.萃取段,3.取样口,4.有机相入口,5.脉冲腿,6~8.脉冲系统, 9.泵1,10.泵2,11~14.储罐,15.有机相出口,16.水相出口。图1 脉冲折流板柱示意Fig.1 Schematic diagram of the pulsed disc-doughnut column
萃取段主体是由3.3高硼硅玻璃制成,内径50 mm,有效段高度1.6 m,配有10个取样口。筛板是由1 mm厚的304不锈钢制成,板间距为25 mm,挡板直径为42 mm,环板内径为32 mm,环板外径为48 mm,澄清段内径为102 mm。通过将一个曲柄连杆控制的活塞连接到脉冲腿,从而产生正弦脉冲。脉冲频率由一个调节器控制,振幅由调整曲柄活塞控制。两相的流速由蠕动泵控制。在液液实验中,使用水作为连续相,煤油作为分散相,并且都在实验前相互饱和。其物理特性如表1所示。
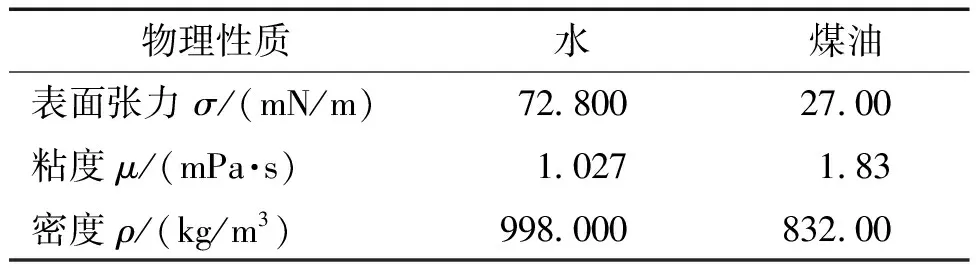
表1 实验系统物理特性Table 1 Physical character of the column
1.2 实验流程
本实验通过体积置换法来测量折流板萃取柱中的存留分数。实验开始时,先在萃取柱中注满连续相,稳定后再向萃取柱中注入分散相,并将两相流速、脉冲强度等操作参数调整到所需值(脉冲强度Af调整范围为 15.7~31.8 mm/s,分散相表观流速Vd变化范围为0.347~1.89 mm/s,连续相表观流度Vc变化范围为0.818~6.71 mm/s)。
当萃取柱达到稳定状态时,记录上澄清段中的两相界面位置,再同时关闭各相的进出口阀门以及脉冲,静置分相后再记录两相界面。计算两相界面的位移。假设所有的分散相都被分离到上澄清段,导致界面下降,存留分数为:
Φ=A1hd/Vtotal
(1)

1.3 存留分数经验关联式
不同的操作条件下,关于脉冲折流板柱中的分散相存留分数的预测方程主要有4个:
1)在没有传质的条件下在脉冲折流板萃取柱中对水-煤油体系下的分散相存留分数的预测方程为[1]:
(2)
式中H是板间距。
2)基于脉冲强度和两相流量的存留分数预测经验方程为[24]:
(3)
(4)
式中:k为不同拟合系数;α为孔隙率;ρ为密度;μ为粘度。
3)基于8种脉冲萃取柱的实验数据[25](不包括脉冲折流板萃取柱),可得平均相对误差EMRE=18.1%时的无量纲预测方程:
xd=ΠΦΨΓ
(5)
其中:
Π=CΠ+[/g(ρc/gγ)1/4]n1
(6)
Φ=[Vd(ρc/gγ)1/4]n2exp[n3Vc(ρc/gγ)1/4]
(7)
Ψ=CΨ(Δρ/ρc)n4(μd/μw)n5
(8)
Γ=CΓen6[l(ρcg/γ)]
(9)
式中:Π为单位质量的输入能量;Φ为由于两相流动引起的相互作用;Ψ为物理性质的影响;Γ为萃取柱几何尺寸的影响;CΠ、CΨ、CΓ分别为不同的常量;n为不同拟合系数;为脉冲能量;γ表示表面张力;l表示特征长度。后续将其中的常数进行重新拟合成功将该式应用到脉冲折流板萃取柱当中[16]。
4)通过在煤油-水,甲苯-水和乙酸乙酯-水3种不同的液液体系以及3种不同的操作区间内的参数变化拟合出2个存留分数的预测方程。其中在过渡区和液泛区的关系式为[4]:
(10)
在方程(2)~(10)中,存在许多高次项,导致这些方程在只考虑1个参数作为变量时,拟合曲线在操作参数的取值范围内趋于线性变化。因此本文使用LASSO方法并主要考虑各个参数的二次函数的作用,回归分析出一个适用范围更广的更加稳定的预测方程,来预测分散相速度,连续相速度和脉冲强度对存留分数的影响。LASSO方法回归方程为:
(11)
构建的待选参数矩阵以及预测方程为:
(12)
Φ=Xθ
(13)
θT=[δ1δ2δ3δ4…δn]
(14)
式中:X为待分析参数矩阵;θ为各个参数前待回归系数。
将各个待选参数值求出并放入矩阵中。再用LASSO方法计算得到待选参数前的系数向量θ并且将某些参数前系数回归为0。最终得到一个关于脉冲折流板萃取柱中存留分数随着分散相速度,连续相速度和脉冲强度变化的二次方程。
2 存留分数结果与讨论
2.1 存留分数变化测量结果
连续相和分散相速度以及脉冲强度对存留分数的影响如图2所示。
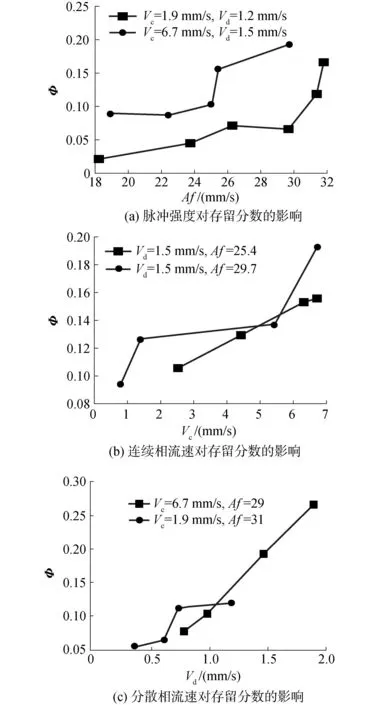
图2 3种参数对存留分数的影响的实验结果Fig.2 Experimental data of the impact of three parameters on dispersed phase holdup effect
由于在液泛时,体积置换法难以对存留分数进行有效测量,图2只记录液泛前的实验结果。图2(a)中分散相存留分数主要随着脉冲强度的增加而增加。因为脉冲强度的增加会导致分散相更容易破碎形成小液滴从而聚集在萃取段内。在脉冲不足时,由于脉冲强度不足以使大液滴破碎,脉冲强度的增加会有助于大的分散相液滴在板段内上升,导致存留分数出现较小的下降趋势[4]。图2(b)和图2(c)分别显示了分散相存留分数随连续相速度和分散相速度变化的情况。在本文的实验条件下两相流速的增加都会促进分散相速度的增加。其中连续相增加会对分散相液滴产生更大的曳力,从而增加存留分数;而分散相流速的增加使更多的分散相进入萃取柱内,从而提高存留分数[17]。
2.2 经验公式拟合结果
将本文预测方程(2)、(3)、(5)、(10)中关于Af,Vd和Vc的相关参数视为变量,其他参数看作常数对经验公式在本文实验数据集上进行重新拟合,得到新的经验公式,并计算出与实验值的相对平均误差,并在图3中比较各个预测方程中预测值和实验值相差情况。拟合方程为:

图3 拟合方程预测存留分数和实验值的比较Fig.3 Comparison of the experimental data with the predicted holdup of refitted correlations
预测1 根据方程(2)重新拟合,EMRE= 29%:
(15)
预测2 根据方程(3)重新拟合,EMRE= 32%:
Φ=7.86×10-7exp(0.38|Af-1.83|)·
(16)
预测3 根据方程(5)重新拟合,EMRE= 33%:
(17)
预测4 根据方程(10)重新拟合,EMRE=16%:
(18)
在图3中可以看到由于在预测1和预测3中分别缺少Vc和Af的作用,导致有一些预测结果与实验值的误差大于100%。预测2的拟合结果大部分都小于实验值,多半分布于图3的下方。预测4的误差最小。各个重新拟合的方程预测结果在操作范围内也趋于变化,相关系数的指数也趋于1和2,由此验证了选用二次方程来预测存留分数随着脉冲强度,分散相表观流速以及连续相表观速度的变化的有效性。
2.3 LASSO拟合结果
通过LASSO方法回归出的二次预测方程为:
0.001 73VcAf+0.002VdAf+0.000 83(Af)2
(19)
图4所示为预测值和实验值的比较,平均相对误差EMRE=11.5%。从图4中可以看出大部分预测值与实验值的误差都在20%以内。图5所示为预测方程计算的存留分数随着脉冲强度以及3个操作参数变化趋势。

图4 LASSO方法拟合方程预测存留分数和实验值的比较Fig.4 Comparison of the experimental data with the predicted holdup of regressed equation

图5 拟合方程和实验结果关于存留分数随着Af,Vc和Vd变化的对比Fig.5 Comparation of experimental holdup and predicted holdup by refitted correlation versus Af,Vc, and Vd
将方程分别对上述3个操作参数求偏导具体分析各个参数对存留分数的影响,如方程为:

0.037 3
(20)
(21)

(22)
图5(a)显示随着脉冲强度的增加,存留分数变化曲线的斜率会逐渐增大,因为由于脉冲强度的增加会加剧两相间的相互作用最终将导致液泛,并且如式(20)所示,当两相流速以及脉冲强度不大时,存留分数对脉冲强度的偏导数会小于0,表明此时存留分数会随着脉冲强度的增加而减少。
图5(b)中显示随着连续相流速的增加,存留分数的上升速度会逐渐减缓。关于连续相速度对存留分数影响的作用方式的描述主要有2种:1)由于连续相流速对分散相液滴的曳力会增大,从而增加存留分数;2)但同时过多的连续相液体流入萃取柱内,会导致分散相的相比减少。这2种作用方式的相互制衡,最终会使得连续相流速对存留分数的影响逐渐减少,如式(21)所示连续相流速前的系数为负数,而且连续相作用项的值在操作区间内都小于其他两项作用的和。
图5(c)和式(22)中显示存留分数随着分散相速度的增加而单调的线性增加,这是由于分散相速度的增加只会引起柱内分散相的通量随之增大从而提高存留分数,并且斜率会随着脉冲强度和连续相流速的增大而增大。
通过上述分析说明LASSO方法拟合出的存留分数预测方程对脉冲强度,分散相流速和连续相流速的作用都有较好的筛选能力,并且能够很好地拟合的变化趋势。
2.4 LASSO方法在其他文献数据集拟合结果
为了分析LASSO方法在存留分数变化预测的适用性,将其分别应用于文献[4]与文献[6]的数据集上进行回归分析。
1)在对3种不同表面张力体系下的数据拟合中引入表面张力σ作为新的参数变量。原文中拟合结果和实验值的平均相对误差为EMRE=7.5%[6]。LASSO拟合结果和文献数据的EMRE=1.9%,拟合方程为:
Φ=0.15-0.000 093σ2+0.000 19σVc+
0.001 8AfVd+0.000 91σVd-0.000 068Afσ+
0.000 18AfVc+0.000 065(Af)2
(23)
Φ=0.12-0.000 069σ2+0.000 54σVc+
0.001 4Vdσ-0.000 037Afσ-0.000 6Af+
0.000 053(Af)2
(24)
2)在3种表面张力且跨越多个操作区间的实验数据上[4],LASSO方法重新拟合的存留分数变化结果如式(24)所示,EMRE=20%。由于该数据集上的操作区间跨度较大,导致LASSO方法拟合出的单个预测方程并不能达到文献[4]中2个分段方程的预测精度(分别为8.8%和9.5%),但也能较好地拟合文献中的实验数据。
3 结论
1)本文在水煤油体系下使用LASSO方法对操作参数进行筛选,拟合出了便于分析解释的多元二次预测方程。通过求解预测方程对应系数的偏导,分析比较了实验数据中各个参数对存留分数的影响,得出对存留分数起主要作用的是分散相流速。
2)通过在相关文献的数据集上进行拟合分析,本文方法适用对存留分数随操作参数变化预测。
3)本文为相关水力学参数的研究和分析提供思路和改进方法。

