时标上的Clifford 值概周期函数与动力方程的Clifford值概周期解
赵莉莉
(云南大学 数学与统计学院,云南 昆明 650091)
0 引 言
神经网络能够从人脑的神经系统结构出发,研究大脑的工作机制,进而揭示人工智能的本质,它是在许多学科的基础上发展起来的新兴的、综合性、交叉性很强的学科.自20世纪80年代初期,美国加州理工学院的优秀生物学家John J.Hopfield 博士,建立神经网络的数学模型后,对实值神经网络的研究进入了一个新的高潮时期,取得了大量的研究成果[1-5].虽然实值神经网络在自动控制、模式识别、图像处理、医疗卫生等领域得到广泛应用,但也有其局限性,无法直接处理复数数据,因此,作为实值神经网络的推广,复值神经网络应运而生,解决了一些实值神经网络不能解决的问题[6],再次掀起了神经网络研究热潮,成为一个新的研究热点.文献[7]研究了一类具有时变时滞的复值神经网络概周期解的存在性与稳定性.文献[8]研究了多个复值神经网络在脉冲耦合机制下形成复杂网络系统的全局渐进同步问题.文献[9]研究了一类具有不确定性和时滞的分数阶复值神经网络无源性问题.文献[10]研究了一类具有时滞的分数阶复值神经网络的准一致同步问题.
因在处理几何问题上的优势,以及实际应用价值, Clifford值神经网络已广泛应用于自动化控制、计算机视觉、图像与信号传输过程等领域之中,获得了大量研究成果,成为又一个新的研究热点.文献[11]利用M矩阵的性质和微分不等式技巧,证明了一类带有离散时滞和分布时滞的Clifford值递归神经网络平衡点的存在性、唯一性,以及全局指数稳定性.文献[12]基于Clifford代数,利用图论方法和线性矩阵不等式方法, 对带有随机项的时滞耦合系统的稳定性和同步性进行了研究.研究时标上Clifford值神经网络,一方面即能涵盖连续型神经网络的研究,还能涵盖离散型神经网络的研究; 另一方面,还能将实值神经网络、复值神经网络,以及四元数值神经网络的研究有机地统一在一起.再考虑到,要想更精确地描述动力系统的动力学行为,其概周期解的存在性与稳定性起到了至关重要的作用, 因此,在时标上讨论Clifford值神经网络概周期解的存在性与稳定性,既有理论意义,又有应用价值.
不动点原理是探讨微分系统各类解函数存在性的常用方法之一,为了更好地在时标上使用不动点原理,讨论Clifford值神经网络的概周期解的存在性,需要将时标上的概周期函数的值域推广到Clifford代数空间、建立完备的Clifford值概周期函数空间, 以及构建时标上一阶动力方程的Clifford值概周期解的存在性定理.
1 时标上Clifford值概周期函数的相关概念
定义1[13]设Τ是实数集的一个非空闭子集(时标).前跃算子、后跃算子,以及粗细度函数分别定义如下:
σ(t)=inf{s∈Τ:s>t},ρ(t)=sup{s∈Τ,s t∈Τ称作是左稠密的,是指t>infΤ,且ρ(t)=t;称作是左分散的,是指ρ(t) 时标上的点有以下4种类型1) 即是右稠密点,还是左稠密点,这样的点称为时标的稠密点,此时有ρ(t)=t=σ(t); 2) 右稠密且左分散点,此时有ρ(t) 定义2[13]函数f:Τ→称作是回归的,是指对于所有的t∈Τk,有1+μ(t)f(t)≠0. 函数g:Τ→称作是右稠密连续的,是指g在时标Τ的右稠密点上连续,在左稠密点上左极限存在.时标上全体回归的右稠密连续函数构成的集合记为R=R(Τ,).令 R+=R+(Τ,)={r∈R,1+μ(t)r(t)>0,∀t∈Τ}. 定义3[13]如果r是一个回归函数,则时标上的指数函数er定义如下 其中 从定义3可以得到:其一,当a是一个正常数,且-a∈R+时,由ξμ(τ)(-a)是一个负值函数可得,时标上的指数函数e-a(t,s)关于第一个变元t单调递减,关于第二变元s单调递增; 其二,当r∈R+时,由ξμ(τ)(r(τ))关于r单调递增可得,当t,s是时标上的固定点时,时标上的指数函数er(t,s)关于r单调递增. 定义4[14]称时标Τ是周期时标,是指 Π:={τ∈:t±τ∈Τ,∀t∈Τ}≠{0}. 从定义4可以看出: 其一,Π关于实数的加法是封闭的,且Π的本身也是实数集的闭子集,是一个时标; 其二,在周期时标上,由前跃算子的定义可得:σ(t+τ)=σ(t)+τ,∀t∈Τ,∀τ∈Π; 其三,粗细度函数是周期时标上的周期函数,Π中的每一个元素都是它的周期,从而当a是一个正常数且-a∈R+时,ξμ(τ)(-a)也是一个以Π中每一个元素为周期的周期函数,故 e-a(t+τ,s+τ)=e-a(t,s),∀t,s∈Τ,τ∈Π. 定义5[15-17]g维欧几里德空间g上的实值Clifford代数,定义如下 其中eA=es1es2…esv,A={s1,s2,…,sv},1≤s1 在下文中,用Crd(Τ,Αn)表示从时标Τ到n维Clifford代数空间Αn的全体右稠密连续函数构成的集合. 定义6设Τ是周期时标,且Τ∩Π≠∅.函数f∈Crd(Τ,Αn)称作是Clifford值概周期函数,如果,f的ε-移位数集 E(f,ε)={τ∈Π:‖f(t+τ)-f(t)‖Αn<ε, ∀t∈Τ} 对于每一ε>0,都在时标Τ上稠密.即,对于任意给定的ε>0,存在l=l(ε)∈(0,+∞)∩Π,使得时标上每一个以l(ε)为长度的区间中,都至少存在一点τ∈Π,使得 ‖f(t+τ)-f(t)‖Αn<ε,∀ε>0. 时标取为实数集时,定义在时标上的右稠密连续函数,就是实数集上的连续函数; 而定义在整数集上的任意函数都是连续的,当然也是右稠密连续的,所以,定义6是实变量概周期函数以及概周期序列概念的合理推广. 时标上全体Clifford值概周期函数构成的集合,记为AP(Τ,Αn). 定理1如果f∈AP(Τ,Αn),则f在时标Τ上有界,且是一致右稠密连续. 证对于一个给定的ε≤1,存在l=l(ε)∈(0,+∞)∩Π,使得时标上每一个以l(ε)为长度的区间中,至少存在一点τ∈Π,满足 ‖f(t+τ)-f(t)‖Αn<ε≤1, ∀t∈Τ. (1) τ∈(E(f,ε)∩[t-t0,t-t0+l(ε)]∩Τ). 则t-τ∈[t0-l(ε),t0]∩Τ.因此,‖f(t-τ)‖Αn 在时标中任取2个右稠密点u,t,满足|u-t|<δ.取 则 故‖f(t)-f(u)‖Αn≤‖f(t)-f(t-τ)‖Αn+‖f(t-τ)-f(u-τ)‖Αn+‖f(u)-f(u-τ)‖Αn<ε,即函数在时标上一致右稠密连续. 定理2如果f∈AP(Τ,Αn),则对于任意的ε>0,存在一个正常数l=l(ε)∈Π,使得对于每一个a∈Τ,都存在η∈(0,+∞)∩Π,以及α∈Τ,满足([α,α+η]∩Τ)⊆([a,a+l]∩Τ),以及([α,α+η]∩Τ)⊆E(f,ε). 从而,令α=τ-η0,η=2η0后,可得([α,α+η]∩Τ)⊆([a,a+L]∩Τ),以及 ([α,α+η]∩Τ)⊆E(f,ε). 定理3f,g∈AP(Τ,Αn),则对于任意的ε>0,E(f,ε)∩E(g,ε)是时标中非空的相对稠密集. 由定义6与定理2,设η=η(ε)是周期时标Τ的最小正周期,则可取 Li=li+η(i=1,2),L=max{L1,L2}. τ1=mη∈([a,a+L1]∩Τ)⊆([a,a+L]∩Τ), 本研究以离子液体为反应介质,通过在溶解的纤维素溶液中加入氯乙酰胺和四氧化三铁,制备磁性纤维素。红外、扫描电镜和透射电镜等表征结果表明,氯乙酰胺及Fe3O4均成功负载于纤维素上。所制得的磁性纤维素具备鲜明的层状结构和磁性性能,这有利与提高对亚甲基蓝的吸附能力。 τ2=nη∈([a,a+L2]∩Τ)⊆([a,a+L]∩Τ), τ∈([a,a+L+2Υ]∩Τ). 对于任意的t∈Τ,有 即时标上每一个以L+2Υ为长度的区间中,都至少存在一点τ∈E(f,ε)∩E(g,ε).也就是E(f,ε)∩E(g,ε)是时标中的非空稠密集. 对于任意的t∈Τ,有 ‖f(t+τ)+g(t+τ)-f(t)-g(t)‖Αn≤‖f(t+τ)-f(t)‖Αn+‖g(t+τ)-g(t)‖Αn<ε, 即,τ∈E(f+g,ε), 再由a的任意性,f+g∈AP(Τ,Αn). 根据定理1,概周期函数f,g均在时标Τ上有界.令 即,τ∈E(fg,ε),再由a的任意性,fg∈AP(Τ,Αn). 证设{fm}是Crd(Τ,Αn)中任意一个柯西序列,即,对任意给定的ε>0,存在正整数N,当m,s>N时,有 ‖fm(t)-fs(t)‖Αn<ε,∀t∈Τ. (2) 因为,对于每一个t∈Τ,{fm(t)}是Αn中的一个柯西序列,而(Αn,‖·‖Αn)是一个Banach空间,所以存在f(t), 使得fm(t)→f(t)(m→∞).因此,在(2)式中,令s→+∞, 可得 ‖fm(t)-f(t)‖Αn<ε, ∀t∈Τ. 特别地,有 ‖fN+1(t)-f(t)‖Αn<ε, ∀t∈T. 对于任意给定的ε>0,以及t0∈Τ,由fN+1∈Crd(Τ,Αn),有以下两种情形. 情形1如果t0是右稠密点,则存在δ=δ(t0)∈(0,+∞)∩Π,使得当t∈(t0-δ(t0),t0+δ(t0))∩Τ时,有‖fN+1(t)-fN+1(t0)‖Αn<ε,故 ‖f(t)-f(t0)‖Αn≤‖f(t)-fN+1(t)‖Αn+‖fN+1(t)-fN+1(t0)‖Αn+ (3) ‖f(t)-a‖Αn≤‖f(t)-fmk(t)‖Αn+‖fmk(t)-amk‖Αn+‖amk-a‖Αn<3ε. (4) 从(3)与(4)式,可得f∈Crd(Τ,Αn).即Crd(Τ,Αn)赋予了上确界范数后构成一个Banach空间. 证对于任意的ε>0, 存在充分大的正整数m0,使得对于所有的t∈Τ,有 ‖f(t+τ)-f(t)‖Αn≤‖f(t+τ)-fm0(t+τ)‖Αn+‖fm0(t+τ)-fm0(t)‖Αn+ 即τ∈E(f,ε),再由a的任意性,f∈AP(Τ,Αn). 定理7(AP(Τ,Αn),‖·‖∞)是一个Banach空间. 证根据定理6,AP(Τ,Αn)赋予了上确界范数后是(Crd(Τ,Αn),‖·‖∞)的闭子空间,又由定理5,(Crd(Τ,Αn),‖·‖∞)是一个Banach空间,故(AP(Τ,Αn),‖·‖∞)是一个Banach空间. 引理1[18]设fi∈AP(Τ,Xi),其中每一个Xi(i=1,2,…,n)都是一个Banach空间,则对于每一个ε>0,所有函数f1,f2,…,fn具有一个公共的ε-概周期. 引理2设Τ是一个周期时标.如果存在-a∈R+,t,s∈Τ,r∈Π,则 证由(e-a(t,s))Δ=-a(t)e-a(t,s),可以得到 (e-a(t+τ,σ(s+τ)))Δ+a(t)e-a(t+τ,σ(s+τ))= (a(t)-a(t+τ))e-a(t+τ,σ(s+τ)). (5) (5)式两边同乘e-a(σ(s),σ(t)),再沿着时标·上的区间[σ(s),t]∩Τ积分后,可得 注意到[ep(c,·)]Δ=-p[ep(c,·)]σ,再考虑到Τ是周期时标,σ(t+τ)=σ(t)+τ, 有 (6) (6)式两边同乘e-a(t,σ(s))后,可得 定理8设Τ是一个周期时标,且Τ≠Π.如果f(t)∈AP(Τ,Αn),a(t)∈AP(Τ,+),且则一阶动力方程xΔ(t)=-a(t)x(t)+f(t),∀t∈Τ,一定存在Clifford值概周期解. |a(t+τ)-a(t)|<ε, ‖f(t+τ)-f(t)‖Αn<ε, ∀t∈Τ. 因此,由引理2可得 即x(t)∈AP(Τ,Αn). 本文主要探讨时标上Clifford值概周期函数的相关性质,以及一阶动力方程Clifford值概周期解的存在性.在第1节中,将时标上概周期函数的值域推广到了Clifford值代数空间,并且将现有文献中,要求时标上的概周期函数,首先应是时标上的连续函数,减弱为时标上的右稠密连续函数,拓展了时标上Clifford值概周期函数的应用空间.第2节主要获得时标上Clifford值概周期函数的有界性、一致右稠密连续性,以及关于函数加法、乘法的封闭性.第3节证明了时标上Clifford值概周期函数空间的完备性.在第4节中,利用时标上Clifford值概周期函数的相关性质,得到一阶动力方程Clifford值概周期解的存在性定理. 以本文的结论作为理论基础,使用不动点原理,可以探讨时标上任意Clifford值神经网络概周期解的存在性.第2节中的相关结论,可以用来考察Clifford值神经网络的非齐次项部分是否概周期函数.而第4节中的主要结论,可以用来构造时标上Clifford值概周期函数空间上的自反映射,若该映射还是压缩映射,则由第3节中证明的时标上Clifford值概周期函数空间的完备性,使用不动点定理,可以得到Clifford值神经网络概周期解的存在性.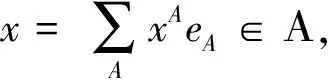

2 时标上Clifford值概周期函数的相关性质
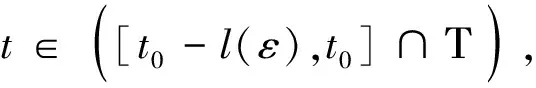



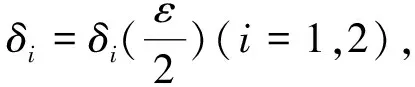








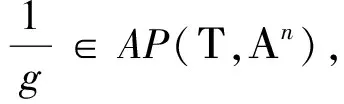
3 时标上Clifford值概周期函数空间

‖fN+1(t0)-f(t0)‖Αn<3ε.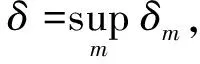
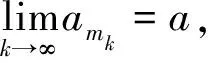
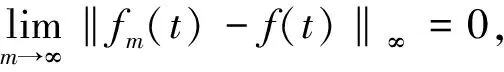

‖fm0(t)-f(t)‖Αn<ε,4 时标上一阶动力方程Clifford值概周期解的存在性



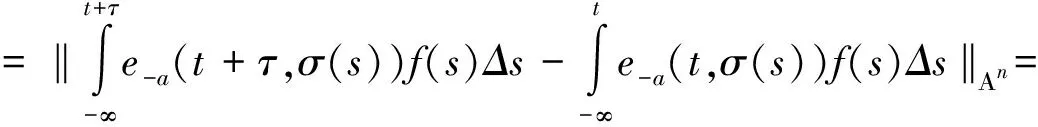
5 结 语

