不同喷管背压下氨气超声速凝结特性

边 江，赵子源，陈俊文，郭 丹，刘 杨，曹学文

（1.中国石油大学（华东）储运与建筑工程学院，山东 青岛 266580；2.中国石油工程建设有限公司西南分公司，四川 成都 610031）

氨作为储氢介质，利用催化技术能够实现“氨-氢”转化，可打破传统的氢储运方式的限制[1-2]。在“氨-氢”绿色能源技术路线中，液氨通过填充有催化剂的高温分解炉被分解成氢气与氮气[3]，由于催化剂效率的限制，分解气中含有大量未分解的氨气等杂质[4]。分解后的混合气经过“氨-氢”分离工序后，得到的氮氢混合气可用于间接氨燃料电池[5]、还原保护气体等，或进一步提纯以生产高纯度的氢气。传统的“氨-氢”分离技术有变压吸附法、吸收法、膜分离法和深冷法。变压吸附法是目前最成熟的“氨-氢”分离技术，应用最广泛，但存在工艺流程复杂，设备投资高及占地面积大等问题；吸收法采用高压循环泵，动力消耗大，操作复杂且工作溶剂有一定毒性；膜分离法操作简单，能耗低，但膜的稳定性差，对原料气杂质含量要求较高，目前无法实现大规模应用；深冷法的运行费用和能耗高，对不同组分原料处理的灵活性差。在国家双碳战略和氢能产业迅速布局的背景下，研发低碳、高效的“氨-氢”分离新技术势在必行。

超声速旋流分离技术是一种新型气体分离技术[6]，其原理是利用可凝蒸汽在高速膨胀过程中产生的低温促使气体成核和凝结。一方面，液滴在旋流叶片离心力的作用下进入收集器，实现气液分离；另一方面，气相经过扩压段激波后温度和压力激增，从而实现动能向压力能的转换[7-8]。该技术具节能环保、无人值守、处理量大和来气适应性强等优势，目前已应用于天然气脱水、脱重烃及液化等领域[9-10]。

Laval喷管是超声速分离器的冷凝部件，国内外学者对Laval喷管内的气体超声速凝结与流动特性进行了较多的研究。曹学文等[11]研究了三元混合物（空气+水+乙醇）的超声速凝结流动特性，模拟结果表明乙醇的存在促进了水的凝结。边江等[12]研究了Laval喷管背压对水蒸汽凝结特性的影响，分析了不同出口背压与进口静压的比值（以下简称“压比”）条件下的凝结规律。LⅠU 等[13]研究了Laval 喷管内激波和边界层的相互作用对水蒸汽非平衡凝结的影响，发现蒸汽在激波串的作用下，成核和多次蒸发的现象多次出现，可以通过减小喷管出口背压来提高喷管的液化效率。氨气在Laval喷管内的凝结研究比较少见，KREMMER等[14]对喷管中氨气的超声速凝结进行了实验研究，发现氨气凝结的过饱和度低于经典成核理论的预测值。JAEGER等[15]的氨气凝结实验证实了氨-水异质成核的可能，发现当水蒸汽含量（质量分数）小于4 × 10-6时，氨呈现出均质成核特性。MATHⅠEU[16]提出了一个新的公式来代替质量分数方程，使用基于表面张力修正的Lothe-Pound（LP）成核模型对喷管中的氨冷凝流动进行了数值模拟，并与实验数据进行了比较，取得了较好的一致性。可以看出，前人对氨气凝结的研究大多关注成核和液滴生长模型的修正，而对氨气的凝结与激波的相互影响研究较少。在超声速分离器出口需要一定的背压以回收压能，但过高的背压可能导致喷管内产生气动激波严重影响分离器的液化效率，因此，阐明氨气在Laval喷管内激波对非平衡凝结的影响对保障分离器正常运行至关重要。

综上，超声速旋流分离技术因其具有低碳环保、清洁高效的优点，已应用于天然气脱水、脱重烃等领域，受到了业内的好评，目前尚无将超声速旋流分离技术用于“氨-氢”分离领域的报道。本文对利用Laval 喷管实现氨气凝结的可行性进行评估，基于空气动力学和冷凝动力学理论建立氨气超声速凝结流动数学模型，采用计算流体力学软件Ansys Fluent 结合物性计算软件REFPROP，研究氨气在Laval 喷管内部凝结流动规律，探讨不同压比对氨气的超声速流动与凝结特性的影响。

1 物理模型

Laval 喷管包括入口稳定段、渐缩段、喉部及扩张段，如图1 所示。亚声速渐缩段采用维氏曲线设计，特征方程见式(1)。渐扩段采用直线段，扩张段采用等坡度直管设计，与喉部光滑连接。喷管具体设计参数见表1。

表1 Laval喷管设计参数Table 1 Design parameters of Laval nozzles

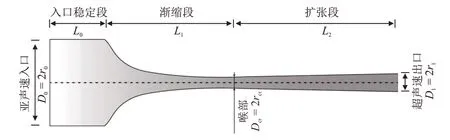
图1 Laval喷管示意图Fig.1 Schematic diagram of Laval nozzles

式中，x为轴向距离，mm；r为径向距离，mm。

2 数学模型

2.1 控制方程

采用欧拉-欧拉模型建立了气液两相的控制方程[17]，包括气相流动方程和液相流动方程。气相流动方程见式(2)～式(4)[18]。

式中，ρv为气体的密度，kg/m3；t为时间，s；xi、xj为横纵坐标分量，m；μ为气体动力黏度，Pa·s；Sm为质量守恒方程源项，kg/(m3·s)；ui、uj为速度分量，m/s；δij为Kronecker delta 数为速度脉动，m/s；Su为动量方程源项，kg/(m2·s2)；E为总能，J/kg；p为压力，Pa；keff为有效导热系数；T为温度，K；τeff为有效应力系数；Sh为能量方程源项，J/(m3·s)。

由于凝结的液滴尺寸很小，可忽略气液相间滑移速度。液相质量分数（Y）控制方程和液滴数目（N，kg-1）有关公式分别见式(5)和式(6)[19]。

式中，SY为液相控制方程能量源项，J/(m3·s)；J为自发成核率，m-3/s。

自发冷凝液滴的质量为凝结核的质量（m1，kg/(m3·s)）和液滴生长的质量（m2，kg/(m3·s)）之和。源项计算公式见式(7)～式(10)，m1和m2的计算公式见式(11)～式(13)[20]。

式中，hv和hl分别为气相和液相的焓值，J/kg；ρl为液相的密度，kg/m3；rd和rc分别为液滴的半径和成核临界半径，m。

2.2 成核模型

JAEGER 等[15]开展了氨气超声速凝结实验，认为LP 成核模型在预测氨气低温成核特性时更为准确。因此，本文采用LP成核模型，见式(14)～式(16)。

式中，vc为临界成核半径对应的液滴体积，m3；mo为氨气的分子质量，kg；kB为玻尔兹曼常数，1.38 × 10-23J/K；σ为表面张力，N/m；qr为成核模型经验常数；nc为临界凝结核含氨分子数目；h为普朗克常数，6.626 × 10-34J·s；I为凝结核的惯性矩，m4；RM为气体常数，8.314 J/(mol·K)；S为过饱和度；ps为对应温度下的饱和蒸汽压力，Pa。

液滴生长过程是一个质量和热量传递的过程，非平衡状态促使氨分子不断在凝结核心表面凝结，凝结释放潜热扰动流场。本文采用Gyarmathy 液滴生长模型[21]计算液滴的生长速度，计算公式见式(17)。

式中，hlv为自发凝结潜热，J/kg；Ts为对应压力下的饱和温度，K；λv为气体导热率，W/(m·K)；Prv、γ和Kn分别为普朗特数、比热比和克努森数。

2.3 表面张力模型

表面张力以三次方的形式存在于成核率公式的指数项中，表面张力的微小变化对成核率有很大影响。根据REFPROP 数据库可知，氨表面张力模型与62 个实验点（197.85～403.15 K）的绝对平均偏差只有0.76%[22]。表面张力计算公式见式(18)。

式中，Tc为氨的临界温度，K；σi和ni为实验拟合系数；k与物质有关，对于氨气，k取2。

2.4 数值方法与网格无关性验证

气体在Laval喷管中的流动属于高速可压缩流动，采用密度基进行求解。采用结构化网格对Laval喷管的流体域进行剖分，并对边界层加密处理。Laval 喷管网格划分情况及边界条件设置见图2。入口和出口为压力边界条件，入口压力为0.17 MPa，入口温度设置为273 K，出口压力根据压比进行设置。壁面为无滑移、无渗流、绝热壁面，对称面采用对称边界。当连续性方程、动量方程、能量方程、湍流动能和耗散速率的残差绝对值小于10-4，进出口质量流量差（包含用户自定义源项）小于0.001%，且以上各个参数不再发生变化时认为计算收敛。

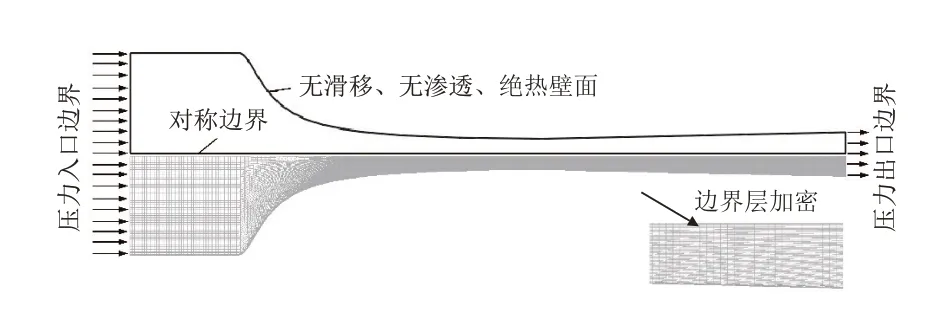
图2 Laval喷管网格剖分与边界条件Fig.2 Meshing and boundary conditions of Laval nozzles

以轴线上的温度和液相质量分数分布作为不同网格数的敏感特征参数，进行网格无关性验证，结果见图3。当网格数大于21358时，敏感特征参数的分布趋于一致。因此，在保证计算精度的前提下为了节约计算资源，选择数目为21358 的网格开展氨气超声速凝结的数值模拟研究。

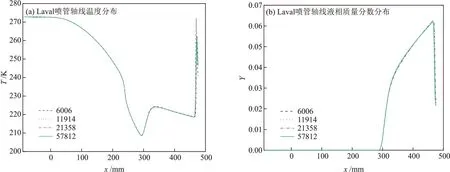
图3 网格无关性验证Fig.3 Grid-independence verification

3 结果与讨论

3.1 模型验证分析

KREMMER[14]通过实验研究了纯氨蒸汽在喷管中的超声速冷凝过程，测量了喷管轴线上的压力分布，利用其论文中的喷管结构和实验数据验证本文数学模型及数值计算方法对氨蒸汽自发凝结研究的适用性和准确性。文献[14]中的喷管收缩段为半径为25.4 mm 的圆弧，喷管喉部宽度为3.683 mm，喷管渐缩角为1°，喷管入口压力和温度分别为0.32 MPa和277.6 K，数值模拟结果与实验数据的对比见图4。

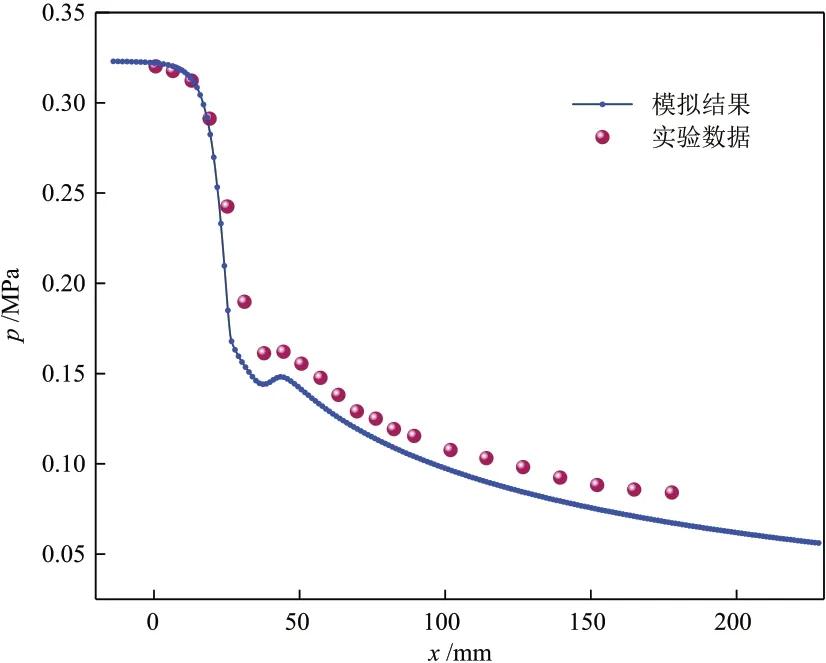
图4 Laval喷管内压力分布的数值模拟结果和实验数据对比Fig.4 Numerical simulation results and experimental data comparison of pressure distribution data of Laval nozzles

由图4可知，气体流动使压力减小，气体达到凝结条件后发生凝结并释放热量，出现凝结激波现象。数值模拟结果与实验结果较为一致，说明本文数学模型和数值方法可以比较准确的模拟出氨气超声速凝结的Wilson点，平均相对误差为11.4%。造成与实验数据误差的原因包括：对实验喷管表面粗糙度的不明确、湍流模型的简化以及成核模型采用理想气体近似等。上述模型验证证实了Laval喷管实现氨气凝结的可行性，也证明了本文采用的数学模型和计算方法对于喷管中超声速凝结流动特性模拟的适用性。

3.2 Laval喷管内氨气凝结可行性分析

在忽略气液相间传质传热的基础上，建立适用于超声速流动的单相流模型（将气相控制方程中的动量，质量和能量源项以及液相控制液滴数目方程和液相质量方程中源项设为0）。基于上述物理模型研究了Laval 喷管实现氨气凝结的可行性，不同入口参数下氨气的相特性见图5。

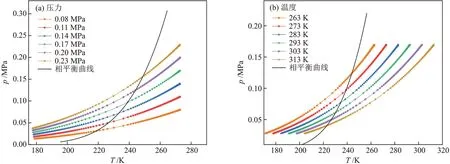
图5 不同入口参数下氨气的相特性Fig.5 Phase characteristics of ammonia at different inlet parameters

由图5 可知，氨气在喷管内膨胀降温，p-T曲线逐渐与相平衡曲线相交（气相区向液相区的转变），标志着氨气开始凝结。随着入口温度的降低和入口压力的升高，p-T曲线在液相区的范围也在增加，这说明调节入口压力和温度有助于氨气的凝结。此外，氨气可液化的温度压力范围较广，Laval 喷管实现氨气液化具有良好的入口参数适应性。

3.3 氨气超声速凝结流动特性分析

在超声速单相流模型的基础上，结合氨气非平衡凝结效应和激波，建立了氨气超声速凝结流动模型。在入口压力0.17 MPa、入口温度273 K 和背压0.09 MPa工况条件下模拟了氨气在Laval喷管中的超声速凝结流动过程，研究了非平衡凝结和激波对氨气凝结特性的影响，模拟所得流动和凝结参数分布，结果分别见图6和图7。

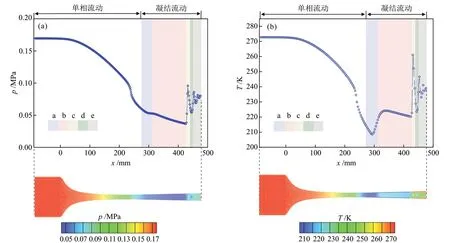
图6 流动参数分布Fig.6 Distribution of flow parameters

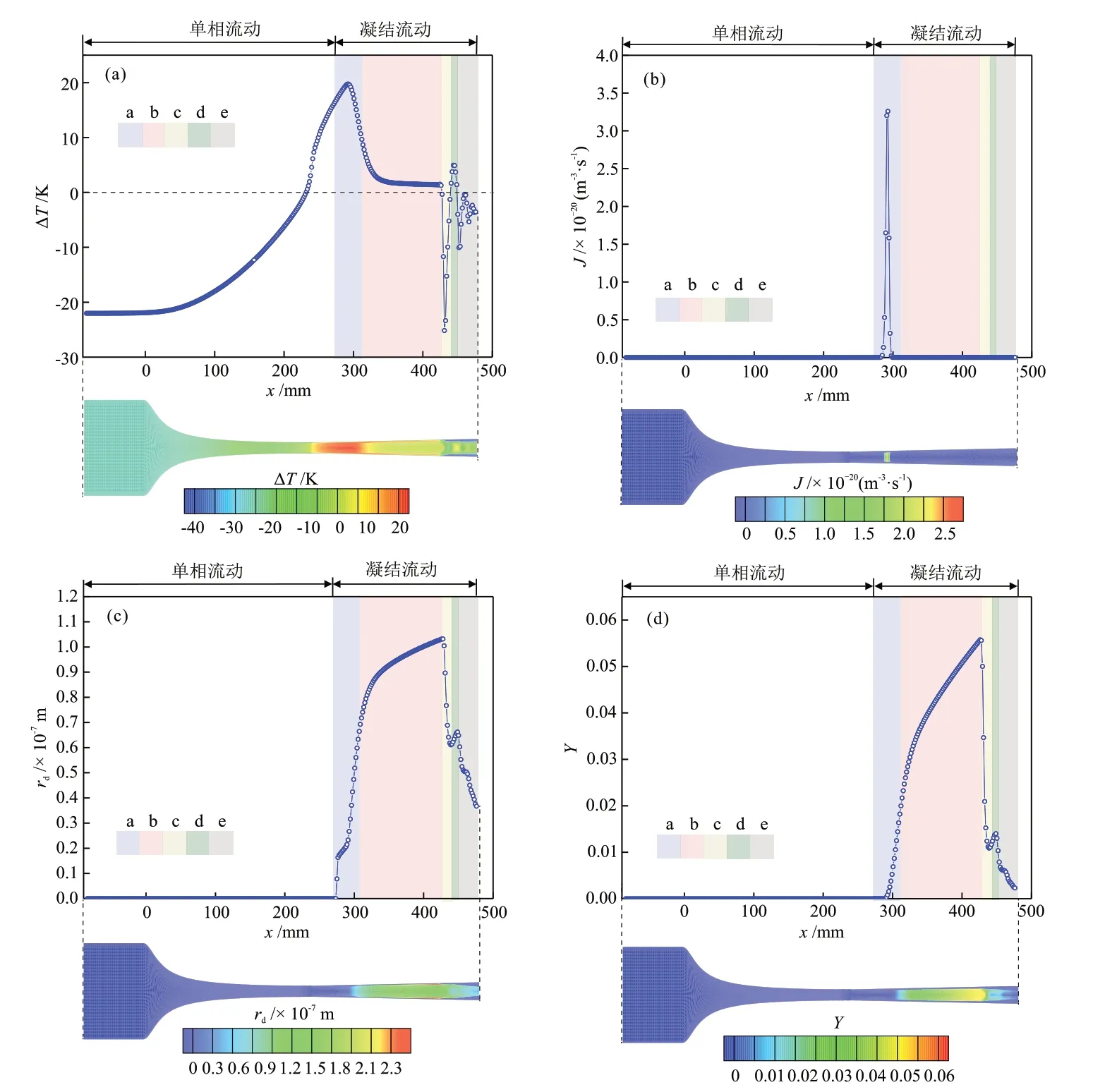
图7 凝结参数分布Fig.7 Distribution of condensation parameters

由图6和图7可知，氨气在Laval喷管中流动并高速膨胀，温度和压力降低，过冷度随之增大，当气体达到饱和状态时由于自由能垒的限制并没有立即凝结而是继续膨胀。氨气在通过喉部之后达到凝结临界状态（a区），并在极短的距离内成核，随后氨气在凝结核上不断凝结，液滴半径和液相质量分数不断增大。氨气冷凝扰乱了流场，导致温度上升和压力增大（a区和b区），过冷度也随之减小。在x=424.5 mm处，激波锋面出现，温度急剧上升，压力急剧增大，过冷度迅速变为负值（过冷度从激波前的2 K迅速降为-24 K），氨液滴没有继续增长而是开始大量蒸发（c 区），液相质量分数迅速从0.055 减小到0.010，液滴半径从1.03 × 10-7m减小到6.07 × 10-8m。在d区，温度和压力达到液滴增长的条件（过冷度大于 0 K，图7(a)），原来部分蒸发的液滴开始继续增长，液滴半径和液相质量分数出现小幅增长。当两相流到达另一个激波锋面时，压力和温度又迅速增大和上升，液滴立即开始蒸发。此后，由于过冷度持续小于0 K，液滴持续蒸发（e区），在喷管出口位置（x=472.8 mm处）处液相质量分数为0.008，喷管凝结效率下降。

3.4 不同背压对氨气超声速凝结特性的影响

保持入口参数不变（0.17 MPa、273 K），研究了背压对Laval 喷管中氨气的流动与冷凝特性的影响，结果见图8。

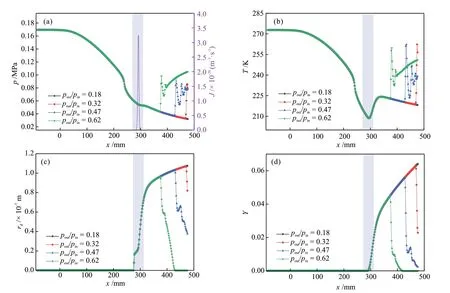
图8 压比对Laval喷管中氨气的流动与冷凝特性的影响Fig.8 Effect of pressure ratios on flow and condensation characteristics of ammonia in Laval nozzles

不同背压下，气动激波前的温度和压力分布基本相同。随着背压的增大，气动激波逐渐产生。如图8(a)和图8(b)所示，背压越大，气动激波的位置越靠前。由于激波位于出口附近，温度和压力的激增并不影响成核区域（图7阴影部分）。当压比为0.18时（对应出口背压为0.0306 MPa），气动激波没有进入喷管，对氨气的超声速流动没有影响。当压比从0.18 增大到0.62 时（出口背压从0.0306 MPa 增大至0.1054 MPa），气动激波逐渐产生并向喉部方向移动，不同压比的气动激波前的液滴半径和液相质量分数分布一致。气液两相流通过激波后，温压跃迁打破了液滴生长的条件，出口处的液相质量分数随之减小。在压比大于0.32时，喷管损失大部分液化性能。随着压比从0.18增加至0.62，喷管出口处液相质量分数从0.064减小至0，喷管完全失去液化能力。

4 结论

本文基于空气动力学和冷凝动力学理论，建立了氨气超声速凝结和流动的数学模型，研究了非平衡凝结和激波对氨的凝结影响规律，分析了不同背压对氨气超声速凝结流动特性的影响，得到以下结论。

（1）氨气在Laval喷管中高速膨胀降温，系统逐渐偏离平衡状态，非平衡状态促使氨气打破成核的自由能垒，凝结核出现。通过狭窄的成核区域后，凝结核周围的氨气分子持续凝结，液滴半径和液相质量分数不断增大。

（2）由于Laval喷管出口处背压高于一定值时，喷管内会出现气动激波，激波与边界层相互作用、相互干涉形成激波串。氨液滴半径和液氨的质量分数在激波前达到了最大值，此后气液两相流经过激波峰面，温度和压力迅速升高和增大，过冷度降为负值。因此，液滴生长条件遭到破坏，凝结液滴开始蒸发，液滴半径和液相质量分数迅速减小。在激波串的波节间存在的低温区，当过冷度大于0 K时液滴半径会出现小幅增大，但之后又会发生蒸发气化。

（3）保持Laval喷管入口参数一定，随着出口背压的增大，气动激波前移，由于激波远离氨气成核区，成核率维持不变，气动激波仅影响氨液滴的生长。随着压比由0.18 增大至0.62，喷管出口处液相质量分数从0.064减小至0，喷管液化效率不断减小直至完全失去液化能力。