中华优秀传统文化融入高中数学教学的实践与探索——以“等差数列的前n项和公式”的教学设计为例

安徽省合肥市教育科学研究院 沐方华 (邮编:230071)

安徽省合肥市第四中学 卞显亮 (邮编:230601)

1 问题的提出

中华优秀传统文化是中华民族的根与魂,教育教学是传承中华优秀传统文化的重要方式.2021年,教育部印发《中华优秀传统文化进中小学课程教材指南》,这解决了“进什么、进多少、如何进”的问题,但是在实际教学实施当中还存在“外在形式多,内在体悟少”的问题,部分老师在教学中虽然设计了不少有关中华优秀传统文化的活动,但是难以将中华优秀传统文化蕴含的核心思想理念渗透其中[1].本文以“等差数列的前n项和公式”教学设计为例,谈一谈如何在教学中渗透中华优秀传统文化.

2 教学过程设计

2.1 创设情境,提出问题

问题1等差数列很早就是我们的一个研究对象,宋代时期所著的《续古摘奇算法卷上》中有这样一个问题:“天数一三五七九,地数二四六八十,积五十五.”你会算吗?你知道古人是怎么算的吗?

师生活动从中华传统数学著作《续古摘奇算法卷上》中一个求和问题出发,学生可以一个一个进行求和.教师引导学生用数列的观点,把这10个数重新排序为:1,2,3,4,5,6,7,8,9,10,转化为等差数列的求和问题.并介绍古人的算法:“并上下数共一十一,以高数十乘之,得百一十,折半得五十五,为天地之数”,引导学生观察1+10=2+9=3+8=4+7=5+6=11,从而得到结果.

问题2据说,200多年前,高斯的算术老师提出了下面的问题:1+2+3+…+100=?你准备怎么算呢?

师生活动学生仿照上面的方法算(1+100)+(2+99)+…+(50+51)=101×50=5050,教师引导学生思考上述方法运用了等差数列的重要性质,当p,q,s,t∈N*,且p+q=s+t时,有ap+aq=as+at.

设计意图借助两个故事,由浅入深,让知识生成更自然.这两个故事蕴含着等差数列的特殊性质,教学时要让学生自己去观察、探索,发现数列的这一性质.教师通过对这两个问题的分析,引导学生用数学的眼光看待问题,也提高学生对中华传统数学的认识,增强文化自信力.

问题3你会计算1+2+3+…+n吗?

师生活动学生类比上述的方法尝试解决问题时,发现需要对n的奇偶进行讨论,学生展示做法,教师点评后总结:

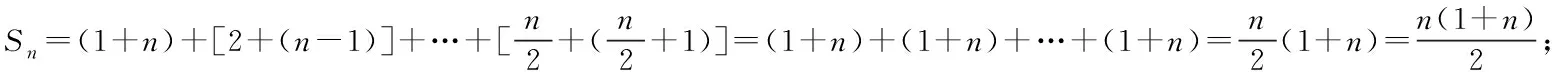
当n为奇数时,n-1为偶数

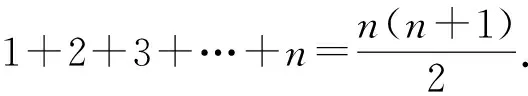
追问若不分类讨论,还可以求和吗?

师生活动教师引导学生将前n项和写为Sn=n+(n-1)+(n-1)+…+1,

再结合Sn=1+2+3+…+n,将上述两式相加,得

2Sn=(n+1)+[(n-1)+2]+[(n-2)+3]+…+(1+n)=(1+n)+(1+n)+…+(1+n)=n(1+n).

教师总结倒序相加法的步骤,通过倒序相加,将复杂的求和问题转化为简单的求和,即转化为n个(n+1)的和,避免了奇偶项的讨论.

2.2 类比探索,整体认知

问题3这种方法能够推广到求等差数列{an}的前n项和吗?

师生活动学生展开讨论.

Sn=a1+a2+…+an-1+an,

Sn=an+an-1+…+a2+a1,

2Sn=(a1+an)+(a2+an-1)+…+(an+a1),

因为a1+an=a2+an-1=…=an+a1,

所以 2Sn=(a1+an)+(a2+an-1)+…+(an+a1)=n(a1+an),

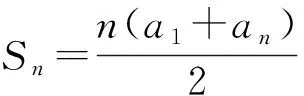
①

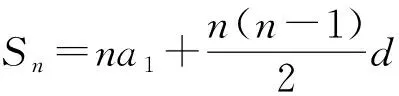
②

追问《九章算术》“盈不足”章的第19问记述了下面的问题:

今有良马与驽马发长安至齐.齐去长安三千里.良马初日行一百九十三里,日增十三里.驽马初日行九十七里,日减半里.良马先至齐,复还迎驽马.问:几何日相逢及各行几何?

师生活动教师引导学生观察良马每天所行里数可看成193与相对于第一天所增加里数的和,可以得到下面的式子:

193+(193+13)+(193+13×2)+(193+13×3)+…++(193+13×14)

=193×15+(1+2+3+…+14)×13

学生仿照上面的方法,从另一个角度得到公式②:

Sn=a1+a2+a3+…+an

=a1+(a1+d)+(a1+2d)+…+[a1+(n-1)d]

=na1+[d+2d+…+(n-1)d]

=na1+[1+2+…+(n-1)]d

设计意图借助刘徽对《九章算术》的注文,由实际问题出发,引导学生从不同角度推导等差数列的前n项和公式,既让学生经历“观察—归纳—猜想”的过程,获得发现公式的体验,又让学生用“倒序相加法”推导公式,体会数学方法的美妙.

2.3 公式应用

例1南北朝数学家张邱建所著的《张邱建算经》中记述了一个问题:现在有一位女子不擅长织布,织布的尺数逐天减少.该女子第一天织5尺布,最后一天织1尺布,一共织了30天,该女子织了多少尺布?

例2已知数列{an}是等差数列.

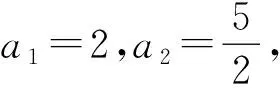
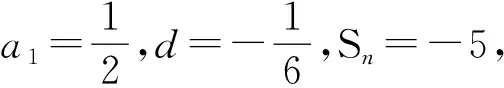
例3已知一个等差数列{an}前10项的和是310,前20项的和是1220,由这些条件能确定这个等差数列的首项和公差吗?

设计意图公式的学习需要在练习中进行巩固.第一个例题选自《张邱建算经》,是等差数列中利用公式①的求和问题,体现我国古代数学家很早就对等差数列有深入研究,进一步加深学生对传统文化的喜爱,有利于提高学生的数学文化,增强文化自信力.

3 教学反思

3.1 充分融合中外优秀传统数学文化,相辅相成服务教学

在教学过程中,我们不可过分强调某某研究成果比国外发现早多少多少年,需要引导学生辩证看待中国传统数学的历史地位和现代价值[2],选取适当的材料进入课堂.本案例选取《续古摘奇算法卷上》中从1加到10这个问题,该问题是学生尚未学习等差数列求和公式就能轻易解决的,进而引出高斯求1加到100和的这个故事,两个材料结合在一起既符合学生认知事物的一般过程,也可以反映出我国古代数学家从简单问题出发推广研究一般性问题的研究思路.

3.2 有机融合中华优秀传统文化,促进知识生成

数学课堂上的教学最重要的是“教数学”,即老师需要在课堂上展现理性思维、科学精神和严谨求实,把数学学科核心素养渗透给学生,所以将中华优秀传统文化融入数学教学是“为教育而文化”,需要老师整合历史材料有机融合在教学的各个环节.本案例中在用另一种方法推导公式②时,可以借助《九章算术》“盈不足”章的第19问作为一个“台阶”,从具体的问题出发,启发学生思考一般性问题的证明,由浅入深,恰到好处.有意识地选用中华传统数学中的问题解决作为思维起点,不仅达到了“教数学”的目的,也在教学中潜移默化渗透了中华优秀传统文化.

3.3 积极发掘中华优秀传统文化,重构促进教学

中华优秀传统文化融入数学教学要坚持精挑细选和创新发展的原则.中华优秀传统文化浩如烟海,不仅仅包括经典著作,还包含人文典故、科技成就、艺术和其他文化遗产,适合教学情景的史料如沙滩上光华内敛的璞玉,需要我们用一双慧眼才能发现,更需要我们精心雕琢,最终才能在课堂教学中绽放光彩.