多普勒非对称空间外差仪探测高层大气风速的三种方法比较研究*

李文文 惠宁菊 李存霞 刘洋河 方妍 李凌青 王彦龙 唐远河

(西安理工大学理学院,西安 710048)

1 引言

地球中高层大气的风速、风速结构和变化特性与空间航空环境、遥感探测水平和日地物理等密切相关[1].随着火星、土星等行星大气风速的遥感探测热潮,高精度探测大气风速已成为研究热点[2].高层大气风速含在气辉辐射的多普勒频移中,通过广角迈克耳孙干涉仪(Michelson interferometer,MI)等光学仪器的成像干涉条纹可提取视线方向上的风速.为了提高测风仪器的稳定性和测风精度,世界范围内的科学家不断努力发展了多种星载和地基光学测风仪器,努力提高测风精度.WINDII(wind imaging interferometer)探测地球上空80—300 km的大气风速是通过压电陶瓷驱动广角MI一臂的动镜步进4次以实现“四强度法”测风,测风精度达到10 m/s[3];PAMI (polarizing atmospheric Michelson interferometer)利用广角MI中在一个周期内的偏振态变化4次实现“四强度法”测风,测风精度达5 m/s[4];WAMI (waves Michelson interferometer)将MI两臂的反射镜都固定,把一臂反射镜分为4个区域再镀反射膜,分别产生0,λ/4,2λ/4,3λ/4 (λ为波长)的步进光程差,实现“四强度法”测风[5,6].WINDII,PAMI和WAMI等仪器均产生干涉圆条纹.多普勒非对称空间外差光谱仪(Doppler asymmetric spatial heterodyne spectroscopy,DASH)将MI两臂的反射镜分别换成闪耀光栅,产生干涉直条纹,采用傅里叶变换法探测地球上空峰值高度250 km的O(1D) 630.0 nm气辉,室内测风精度为1.6 m/s[7];MIGHTI (Michelson interferometer for global high-resolution imaging)也采用DASH思路将MI两臂的两个闪耀光栅的衍射光再相干叠加,采用傅里叶变换法探测高层大气风速,测风精度达1.2—4.7 m/s[8,9].中国科学院西安光学精密机械研究所的陈洁婧等[10]分析了DASH傅里叶变换法测风中窗函数的选取对测风精度的影响,中国科学院光电技术研究所的彭翔等[11]对DSAH测风的复合光程差相移解算方法的前提也是由傅里叶变换法从干涉图中提取位相差.宁通[12]将DASH的干涉图用傅里叶级数拟合而提取风速,测风精度为12.6 m/s.所以目前从DASH干涉条纹中提取风速有傅里叶级数法[12]和流行的傅里叶变换法[7].

本课题组研制的地基气辉成像干涉仪GBAII(ground based airglow imaging interferometer)成功探测地球上空90—100 km 的大气风速、温度、密度等信息[13-15],通过改进,利用“四强度法”测风精度能达到4—6 m/s[16].本文将GBAII的两臂换成闪耀光栅,改造为GBAII-DASH系统,首次提出用“四强度法”反演GBAII-DASH的大气风速.比较研究DASH测风的3种方法——傅里叶级数法、傅里叶变换法和“四强度法”获取风速的原理、仪器正演和野外拍摄O(1S) 557.7 nm气辉的风速数据反演及测风精度.

2 DASH探测高层大气风速的3种方法

2.1 DASH测风关键—提取干涉条纹位相差

DASH光路如图1所示,待测气辉经准直透镜Lens1后入射至立方分束器(beam splitter,BS)分成两束光强相同的相干光,经闪耀光栅G1和G2衍射后原路返回BS,再到CCD上成像干涉.轴向光以θ角入射到光栅上,如果光线以θ角沿原方向衍射回来,此时波数称为光栅的Littrow波数(σL),此角θ称为Littrow角.如图2所示的平面反射式光栅的夫琅禾费衍射光强为[17]

图1 DASH的光路图[7]Fig.1.Optical path diagram of DASH.

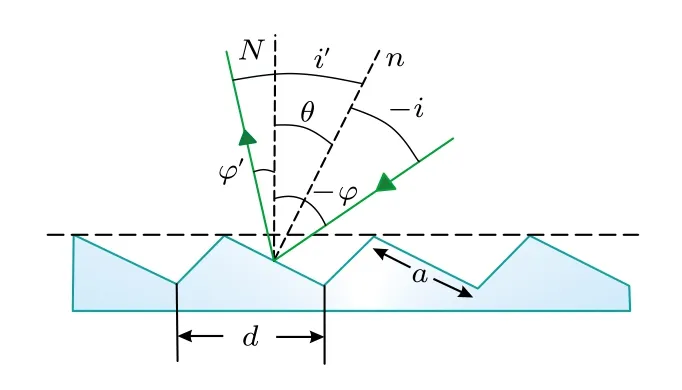
图2 闪耀光栅结构图Fig.2.Blazing grating structure diagram.

其中a是光栅小反射面的宽度;d是光栅常数;i和i'是光线关于小反射面法线n的入射角和衍射角,φ和φ'是光线关于光栅法线N的入射角和衍射角;i,i',φ和φ'的正负规定按光线以锐角转向法线的顺时针为正、逆时针为负.πa(sini+sini')/λ是单缝衍射因子,πd(sinφ+sinφ')/λ是缝间干涉因子.缝间干涉确定主极大峰值强度、位置和数目,满足光栅方程d(sinφ+sinφ')=kλ (k=0,±1,±2,···)时衍射产生主极大,考虑反射角与衍射角的正负,|sinφ+sinφ'|不可能大于1,这就限制了主极大数目.主极大的最大级|k| ＜d/λ,故一般选取第1级衍射.

入射到DASH光束的波数若是σL,过BS后的两光束经光栅衍射后返回的出射波面都与光轴垂直,相位差为0;若入射光波数不是σL,两出射波面的传播方向与光轴都有一夹角±γ,形成斐索干涉条纹,此时φ=θ,φ'=θ -γ,将其代入光栅方程,便可求出γ.斐索干涉条纹经透镜Lens2后成像于CCD靶面,此时斐索干涉条纹的空间频率为

若高斯线型气辉入射到DASH上,其干涉方程为

其中,光程差Δ=4tanθ[x+ΔL/(2tanθ)] (单位为cm),x是CCD探测器的像素点位置坐标,ΔL是两臂的路径差,如图1所示,2ΔL是干涉仪的固定光程差.B(σ)=B0exp[-4ln2(σ-σ0)2/ω2] 是光源辐射谱,B0=(2/ω)/(ln2/π)1/2,零风速波数σ0与波长对应关系σ0=1/λ0,ω=[(7.16×10-7)2×]1/2是高斯线型气辉的半高宽,其中T是热平衡时的大气温度(单位K),M是发光物质的原子量.

如果视线方向的气辉粒子对探测器有相对运动速度v,则波数变为σ=σ0(1+v/c),根据(3)式及多普勒频移,得到含大气风速项的相位φv:

零风速相位φ0为

由(4)式可知,DASH干涉仪测风的关键是探测出干涉条纹的相位差.国际上采用傅里叶级数和傅里叶变换两种方法从DASH干涉图中提取相位量来反演大气风速.

2.2 傅里叶级数法测风

对单一谱线入射的气辉光源,因为傅里叶级数可转变成余弦函数,积分变为求和,由(3)式可知干涉强度I是像素点x的余弦函数[12]:

首先对DASH干涉图进行傅里叶拟合,得出傅里叶级数方程:

根据傅里叶级数三角变换,将(7)式转换成如下余弦函数[12]:

其中ci是权重系数;φi可由(8)式中的系数求得,φi=-arctan(bi/ai);f是频率.余弦函数(8)中包括i个不同频率的余弦项,φi是第i项余弦项的初始相位.

当被拍摄的气辉谱线是单一波长时,可用一级谐波作为含该主要信息的数学模型,即当i=1时,(8)式中的φ1项是(6)式中的4π(σ -σL)ΔL项.当干涉图是零风速的光所成像时,φ1便是(5)式所示的零风速相位φ0;当干涉图是含有多普勒频移的光所成像时,φ1便是(4)式和(5)式中有大气风速相位和零风速相位之和φ1=φv+φ0.傅里叶级数法分别对零风速和含风速干涉图的数据进行傅里叶级数拟合,求出v=0的φ1及风速v≠ 0的φ1,两者相减得到φv,结合(4)式即可求出视线方向上的风速.

2.3 傅里叶变换法测风

当DASH干涉仪接收连续谱线简化为几条离散光谱时,则(3)式写成[7]:

其中j指的是第j条谱线,Sj与探测器上干涉图条纹亮度成正比,Ej(x)依赖光谱线型和光程差的包络函数,κj=4(σj-σL)tanθL是每条谱线中心σj的外差空间条纹频率,φj=4π(σj-σL)ΔL是固定光程差2ΔL引起的相位,δφj是每条谱线多普勒频移导致的相位频移量.

选择合适的光谱带、Littrow波数和ΔL后,(9)式的傅里叶变换产生一个复频谱,在空间频率κj和-κj附近有局部分离良好特性.分离出这些特性,如令j=0,通过归零除了+κ0附近局域内的光谱元素,有效消除了所有干涉图贡献,仅保留一个指数项,因此在傅里叶逆变换后得到[7]

相位项可从(10)式的虚部和实部之比得到

将(11)式计算结果减去零风速相位2πκ0x+φ0,便得到相移δφ0,根据(4)式求出该谱线在视线方向上的风速,这就是国际上常用的傅里叶变换测风方法.

2.4 “四强度法”测风

WINDII用压电陶瓷驱动MI的“动镜”实现相位的4步进测风[3],而DASH结构中没有移动部件,我们提出也可以用“四强度法”测风,阐述如下.如图3所示的简化GBAII-DASH光路,非Littrow波长光入射时,两出射光的波面间会有夹角2γ,如图4所示.两出射光到达CCD相同像素点时,若两者的光程差正好是一个λ的长度,或者是一个λ的整数倍时,探测器CCD靶面上会形成亮条纹.故对于GBAII-DASH来说,我们用两出射光到达CCD相同像素点的光程差来实现相位的四步进法测风.

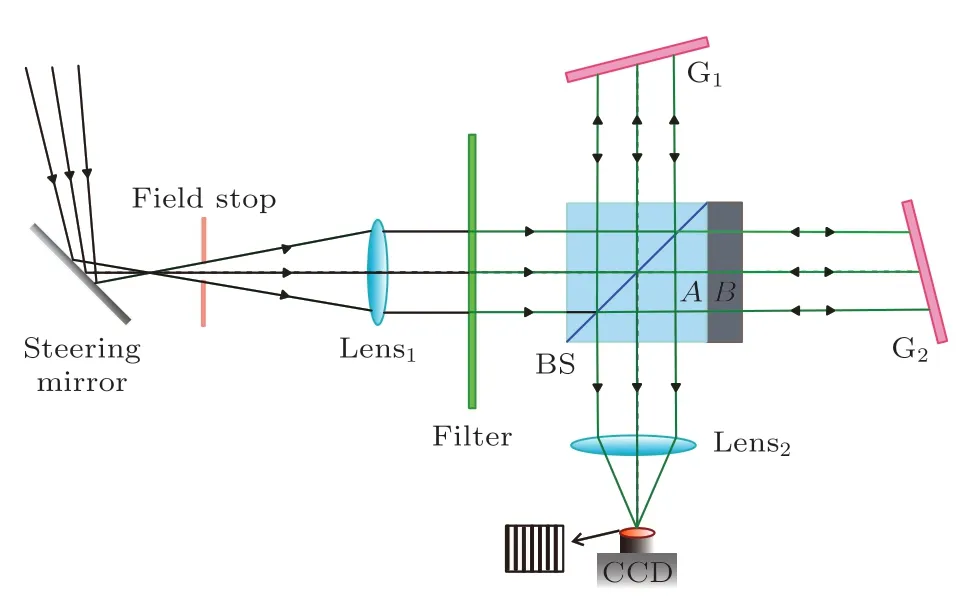
图3 GBAII-DASH的光路图Fig.3.Optical path diagram of GBAII-DASH.

图4 两出射波面夹角示意图Fig.4.Angle of emergent wave surface.

高斯线型气辉经广角MI后所成干涉图的强度为[3]

其中σ0是零风速时的波数,T是大气温度,Q=(π2ω2)/4Tln2,是高斯线型气辉的半高宽,M是以σ0为中心的发射线的物质的原子量.令条纹调制度V=exp(-QTΔ2),则

根据多普勒效应σ=σ0(1+v/c),将(13)式的σ0换成σ,光程差Δ分为含固定光程差Δ0、含风光程差Δv、步进光程差Δ′之和Δ=Δ0+Δv+Δ′(且Δ0≫Δv,Δ′),则由(3)式可得Δ0=2ΔL,Δv=Δ0(v/c),Δ′=4xtanθ,3种光程差对应相位分别为φ0,φv,φ'.因此(13)式变为

当φ'=0,π/2,π,3π/2 (对应Δ′=0,λ/4,2λ/4,3λ/4,条纹周期很小,量级是10-5,为了防止步进太小而被吞掉,会以(π/2+2kπ)(k是整数)方式步进),代入(14)式得4个强度值:

由此得到

由(18)式得到φ0+φv后,减去零风速定标所确定的φ0(定标选择cos2πσ0Δ0=1条件得Δ0,亦即φ0=2kπ (k为整数)),就得出含有风速的相位φv,再根据(4)式即可求出视线方向上的风速,这便是我们提出的GBAII-DASH的“四强度法”测风法.

3 三种测风方法的正演结果

利用计算机仿真正演GBAII-DASH干涉仪的光学成像过程,需要考虑大气传输模型和仪器模型等诸多部分,这里只对大气传输模型及仪器模型进行比较研究.

本系统以氧原子O(1S) 557.7 nm作为目标谱线,其体发射率分布为[18]

式中Ve,Vf代表地球上空E层(100—300 km)和F层(300—500 km)的峰值体发射率(单位photons·cm-3·s-1),χ是太阳天顶角(单位(°)),be=(h-He)/We,bf=(h-Hf)/Wf,h是海拔高度,He和Hf分别是E层和F层的峰值高度,We和Wf为E和F层气体的标高.

GBAII-DASH探测系统使用窄带滤波片的滤波函数与波长λ、入射角θ的关系为[19]

其中Δλ是半高宽,λ0是中心波长,n是滤光片的有效折射率.

(14)式中的φ0可由零风速定标而确定,选择适当的固定光程差2ΔL,令φ0=2kπ (k为整数),而不出现在余弦函数中,则展开干涉强度函数(14)式得

令J1=I0,J2=I0Vcosφv和J3=I0Vsinφv,则CCD的第l行j列像素上获得的模拟结果为

其中R是仪器响应度,2ΔLij是固定光程差,Nnoise是输出信号中存在的噪声.

仪器正演仿真时我们选取CCD是1024 × 1024面阵探测器,单像素尺寸24 μm × 24 μm,固定光程差2ΔL=7.495 cm;光栅Littrow波长550 nm,Littrow角14.3°,刻线密度900 L/mm.模拟西安上空峰值高度为98 km的O(1S) 557.7 nm气辉.假设一个大气风速值,得到正演仿真干涉图后,分别用傅里叶级数法、傅里叶变换法和“四强度法”从干涉图中提取风速.

3.1 傅里叶级数法测风的正演结果

干涉条纹进行一级傅里叶级数拟合后的结果如图5所示,图6是图5的局部放大图,从图6可明显观察到,因为风速而导致的干涉图相位的频移.

图5 干涉图的傅里叶级数正演结果Fig.5.Fourier series forward results of interferograms.

图6 图5中正演结果的局部放大Fig.6.Local amplification of forward results in Fig.5.

假设以10 m/s为风速间隔的0—100 m/s风速,得到正演干涉结果,对风速为0 m/s干涉结果进行傅里叶级数拟合后的方程式如下:

同理可得出其他风速的傅里叶级数拟合方程.根据(7)式和(8)式可求出不同风速的相位φ,此时0风速相位φ0就是GBAII-DASH系统固定光程差2ΔL导致的相位,则不同风速导致的相位频移量φv=φ -φ0,根据公式v=cφv/4πΔLσ0求出风速如表1第2列所示,平均测风相对误差是2.98%.

表1 三种测风方法的正演结果Table 1.Forward wind speed results by three methods.

3.2 傅里叶变换法测风的正演结果

对干涉数据进行傅里叶变换后,利用(11)式分别求出不同风速的干涉图上各像素点的相位,如图7所示.选取第387个像素点的相位进行分析,即x=387时,不同风速的相位Φ=2πκx+φ0+δφv.而0风速的相位就是系统固定光程差2ΔL导致的相位Φ0=2πκx+φ0,则不同风速导致的相位频移量δφv=Φ -Φ0,用v=cδφv/4πΔLσ0求出风速如表1第3列所示,平均测风相对误差是4.67%.

图7 傅里叶变换的相位分布图Fig.7.Phase distribution diagram of Fourier transformation.

3.3 “四强度法”测风的正演结果

用“四强度法”反演风速,首先需确定如图4所示起点I0的坐标x0,然后以两出射光到达CCD像素点x0的光程差为起点,令光程差依次步进λ/4或者kλ+λ/4 (k是整数),故x0的选取很重要.干涉图的强度I是关于CCD像素点坐标x的函数,将GBAII-DASH干涉仪中固定光程差2ΔL所导致的相位φ0,代入到干涉图方程中,求出相位是φ0的像素点坐标x,则此x便是步进的起始点坐标x0.

假设风速为50 m/s得到仿真干涉数据的拟合函数如图8的绿色曲线所示,因为干涉图的周期很小,一个周期量级为10-5,为3个像素大小,每次步进1/4个周期,即3/4个像素的距离,这个距离太小而被吞掉,故我们将周期性函数进行拉伸,得到拉伸后的“四强度法”拉伸函数结果如图8的红色虚线所示.经过拉伸后再步进,确定出x1,x2,x3,x4,各像素点对应的强度值I1=0.1793,I2=0.8836,I3=0.8207和I4=0.1164,利用tan(φ0+φv)=(I4-I2)/(I1-I3)和反正切求出v=50 m/s时φ=0.8745 rad.

图8 函数拉伸后的“四强度法”Fig.8.Four steps of phase determination.

用同样的方法处理其他风速的干涉图数据,得出相位.将0风速的相位φ0作为GBAII-DASH固定光程差2ΔL所对应的相位,则风速导致的相位频移量是φv=φ -φ0,利用v=cφv/4πΔLσ0求出正演风速如表1第4列所示,平均测风相对误差是3.00%.

3.4 三种测风方法正演结果的误差

上述正演研究中未考虑噪声的影响,但是实际拍摄气辉的成像干涉图存在多种噪声,从干涉图提取相位之前需对原始数据去噪和平场.为了探测噪声和平场对3种方法测风误差的影响,我们在正演过程中对上述风速的干涉图人为添加均值为0、标准差为0.1的高斯噪声,对各数据进行平场处理后,利用傅里叶级数、傅里叶变化和“四强度法”进行正演,得到正演风速结果如表2所示,3种方法得到的平均相对误差分别为2.30%,11.66%,2.27%.可见干涉图存在噪声时,傅里叶变换法的测风误差相对较大,傅里叶级数法和“四强度法”测风的测风精度高,但两种方法在测风间隔是10 m/s时的测风误差相近,为了更好地区分出傅里叶级数法和“四强度法”的测风精度,我们继续分析测风间隔在1 m/s和0.1 m/s时两种方法的测风误差.

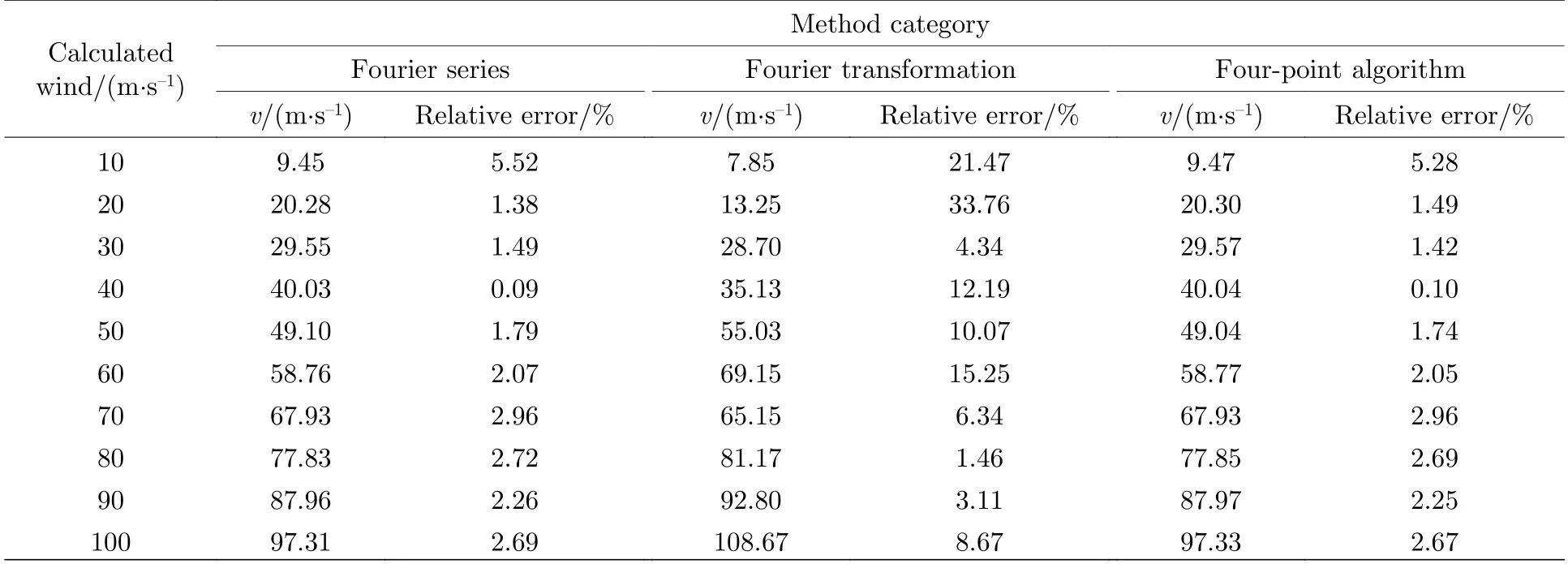
表2 加入噪声后的3种测风方法的正演误差Table 2.Speed Error after adding noise by three methods.

模拟含有噪声的以1 m/s为间隔的风速是31—39 m/s和以0.1 m/s为间隔的风速是30.1—30.9 m/s的干涉图,用傅里叶级数法和“四强度法”从干涉图中提取风速,求出误差,结果如图9所示.从图9可以看出,1 m/s为风速间隔时“四强度法”的平均测风相对误差是2.20%,明显低于傅里叶级数法的平均测风相对误差3.55%,以及0.1 m/s为风速间隔时“四强度法”的平均测风相对误差是2.69%,也明显低于傅里叶级数法的平均测风相对误差4.15%.故“四强度法”的测风精度更优于傅里叶级数法测风.

图9 两种方法的测风误差Fig.9.Wind measurement error of two methods.

从正演和增添噪声的上述结果可见,傅里叶变换法测风的误差较大.傅里叶变换法测风时,将窗函数频谱卷积过程中导致复原干涉图的包络与理想干涉图的包络在小光程差和大光程差区域发生明显变形,直接影响干涉相位的计算,导致测风误差大.减小误差的办法是选择中心区域的光程差点能较准确反演出风速[20].

“四强度法”测风时,是通过(18)式的反正切求出相位,其中(I4-I2)和(I1-I3)已经把干涉图的背景噪声和直流部分统统减掉,故对数据平场后测风精度较高;况且“四强度”法测风计算简便,不用考虑窗函数因子的不确定性带来的测风误差.

4 室外实验3种方法的反演结果

采用图3所示的GBAII-DASH光学系统(实物见图10),于2023年4月19日凌晨1—3点在陕西西安临潼洪庆山顶(海拔1250 m,34°19′52′′ N,109°16′56′′ E)拍摄O(1S) 557.7 nm气辉的成像干涉图如图11所示,图11(a)是GBAII-DASH的0°天顶角所拍的结果,用于零风速定标,图11(b)是天顶角为45°时拍摄的O(1S)气辉成像干涉图.

图10 GBAII-DASH 的实验系统Fig.10.GBAII-DASH system in the laboratory.

图11 GBAII-DASH拍摄O(1S) 557.7 nm气辉的成像干涉图 (a) 0°天顶角时拍摄的干涉图;(b) 45°天顶角时拍摄的干涉图Fig.11.Imaging interferogram of O(1S) 557.7 nm gas glow obtained by GBAII-DASH: (a) Interferogram taken at 0°zenith angle;(b) interferogram taken at 45° zenith angle.

通过去噪和平场等措施后,分别用傅里叶级数法、傅里叶变换法和“四强度法”提取图11气辉干涉图的大气风速如表3所列.分别用傅里叶级数法、傅里叶变换法和“四强度法”测得当晚西安上空98 km的一维风速为32.21 m/s,43.55 m/s和32.17 m/s.

表3 三种方法反演室外测风结果Table 3.Inversion wind speed outdoor experiment by three methods.

5 结论

基于DASH探测高层大气风速,比较研究了傅里叶级数法、傅里叶变换法和“四强度法”提取风速的原理、正演、噪声和反演等内容,3种方法探测风速均从DASH光学系统所得斐索干涉条纹的相位差变换而来,结论如下:

1)模拟以10 m/s为风速间隔的风速0—100 m/s的正演斐索干涉图,用傅里叶级数法、傅里叶变换法和“四强度法”得到正演风速值,计算得到3种方法的平均测风误差分别为2.93%,4.67%和3.00%.

2)人为添加均值为0、标准差为0.1的高斯噪声后,假设风速是0—100 m/s,用傅里叶级数、傅里叶变换和“四强度法”分别对平场后的数据进行正演,得到平均相对误差分别为2.30%,11.66%,2.27%.

3)以1 m/s为间隔模拟风速31—39 m/s,得到含高斯噪声的正演斐索干涉图,用傅里叶级数法和“四强度法”得到正演风速值,并得到平均测风误差分别为3.55%,2.20%;以0.1 m/s为间隔的风速30.1—30.9 m/s,模拟得到含高斯噪声的正演斐索干涉图,用傅里叶级数法和“四强度法”的平均测风误差分别为4.15%,2.69%;“四强度法”的测风误差都小于傅里叶级数法的测风误差.

4)利用GBAII-DASH拍摄西安上空98 km的O(1S) 557.7 nm气辉,得到天顶角为0°和45°的成像干涉图,再用傅里叶级数、傅里叶变换和“四强度法”得到风速的反演结果分别为32.21 m/s,43.55 m/s和32.17 m/s.

5)从DASH的正演、反演数据结果看,我们提出的“四强度法”探测高层大气风速的结果较好,计算简便且测风精度相对较高.