折线型折流板间隙内气液流动及分离特性
马 峰, 伍丹丹
(1. 山西工程科技职业大学 设备工程学院, 山西 太原 030619; 2. 中石化中原油田分公司石油工程技术研究院, 河南 濮阳 457001)
在天然气开发领域及油气田地面工程中,管道内的水合物很有可能产生段塞流,对下游压缩机等设备造成巨大危害[1].因此,有必要对天然气进行气液分离处理,减少对管道的堵塞及腐蚀[2].
常规的惯性式气液分离设备是天然气站脱水工艺中最常用的分离设备,折流板作为惯性式气液分离设备中重要的分离元件,目前许多学者已经对其进行了大量研究.早期的研究大多以试验为主[3],如Monat等[4]将激光干涉仪应用到了波纹板除雾器的分离性能试验中;随后,Mcnulty等[5]在此基础上对不同折流板型式的波纹板除雾器分离性能进行了比较分析.同时,很多学者通过数值模拟的方法对其进行了研究.如Wang等[6]数值分析了各种不同结构型式的折流板分离器内的压降特性、湍动能、液膜厚度等参数变化,提出了折流板分离器的分离效率和各准则数之间的关系.Wang等[7]数值分析了液滴直径与分离速度的之间的关系,发现折流板的分离效率与液滴直径成正相关.总之,目前针对传统惯性式气液分离设备的折流板已经进行了大量研究,但上述研究没有充分考虑液滴与折流板叶片的碰撞以及碰撞后续发展结果,不能很好地描述折流板间隙内的流场情况以及各参数对分离性能的影响,无法准确地指导实际工程
因此,基于DPM与拉格朗日液膜模型,考虑液滴与折流板叶片的碰撞以及碰撞后续发展结果,建立了折线型折流板间隙内气液流动分析模型,通过试验数据验证了模型的准确性.研究了折流板内部流场情况,分析了折流板运行参数对折流板分离性能的影响规律.
1 数理模型建立
1.1 物理模型建立
建立了折流板间隙内气液流动模型,由于流体沿着折流板横向通道内流动状况相似,故把流场简化为平面的二维流动.图1为截取四个叶片、三个流体通道的二维结构示意图,其中,折流板进出口部分长度S=50 mm、排液孔直径H=3 mm、折流板总高度h=173 mm、叶片转折角θ=63°、板间距W=20 mm.
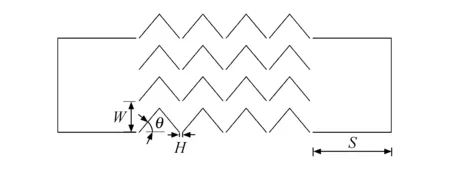
图1 折流板二维结构示意图Fig.1 Two-dimensional structure diagram of deflector
1.2 数学描述
考虑到计算成本问题,进行适当的简化:1) 由于入口的流体速度较小,故可视空气为不可压缩气体处理.2) 在折流板内实际上是含有液滴的气液两相流的流动过程,由于空气体积分数远大于水相,水以液滴形式随空气在折流板通道内流动,因此,将空气视为连续相,水视为离散相.3) 忽略液滴相变及传热特性.4) 由于液滴直径很小,忽略液滴质量.综上考虑,建立了数值模拟基本数学模型.
1.2.1空气流动
在折流板通道内流动的空气为不可压流,满足质量守恒方程.不可压缩流体湍流时均流动的连续性方程可表示为
(1)
式中:ug,x为空气流速在x方向上的分速度,m/s;ug,y为空气流速在y方向上的分速度,m/s.
空气在折流板通道内的流动时需满足力平衡方程.根据牛顿第二定律,空气在折流板通道内流动过程中的惯性力等于空气重力、单位质量空气表面压力、空气粘性力、湍流应力的合力.由此,在惯性参考系中的空气动量守恒方程表示为
(2)
式中;p为静压,Pa;gy为y方向的重力加速度,m/s2;μ是空气动力粘度,Pa·s;μt是湍流动力粘度Pa·s.
式(2)中湍流动力粘度μt可表示为
(3)
式中:kg、εg分别为空气的湍动能和湍动能耗散.
采用Realizablek-ε湍流模型,湍动能方程和湍流耗散率方程可分别表示为
式中:σk和σε分别为湍动能和耗散率的有效普朗特数的倒数,根据文献[8]取σk= 1.0,σε= 1.3;Cμ不再是常数,Gg,k为空气的平均速度梯度引起的湍动能的生成项,两者的计算式分别表示为
(6)
(7)
式中:U*是关于平均应变率和旋度的函数,表1列出了相关参数的选取原则[8].

表1 Realizable k-ε湍流模型中的各参数值
1.2.2水滴流动
采用DPM模型对液滴进行分析,为了简化计算,忽略液滴间的作用力,并将液滴视为球形液滴.
1) 液滴受力平衡方程
基于Lagrangian参考系,液滴受力平衡方程式为
(8)
式中:g为重力加速度,m/s2;ρg、ρl分别为空气和液滴的密度,kg/m3;Fx为作用在液滴上单位质量的附加力,m/s2,包括萨夫曼升力或布朗力等.本文中由于气流密度与液滴密度比值小于1,因此虚拟质量力和压力梯度力可忽略不计.对于亚微米粒子可考虑将布朗运动的影响算入在附加力项中.由于Saffman升力仅适用于亚微米颗粒情况,且基于剪切场,因此式(8)中Fx的值为0,可以忽略不计.FD为单位质量的液滴颗粒所受到的曳力.故式(8)可化简为
(9)
将液滴视为球形,则单位质量的液滴受到的阻力公式为
(10)
式中:τr为液滴的弛豫时间,s;ug、ul分别为空气和液滴的速度,m/s.
液滴的弛豫时间根据文献[9]可表达为
(11)
式中:μ为空气动力粘度,N·s/m2;dl为液滴直径,m;Re为相对雷诺数,是一个无量纲准则数;CD为阻力系数.
式(11)中的相对雷诺数Re和阻力系数CD可表示为
式中:a1、a2、a3是受液滴材料影响的常数,参照表2中Morsi和Alexander给出的参数选取[10].

表2 不同雷诺数时a1、a2、a3的取值
2) 液滴轨迹方程
液滴每运动到一个新的位置,都对应有一个新的速度,而液滴轨迹方程表示为
(14)

当空气为湍流流动时,式(15,16)中的空气速度ug加入脉动速度项.而对于k-ε湍流模型,假设脉动速度服从高斯概率密度分布.在空气湍流涡的寿命期内,脉动速度的计算式为
(17)

3) 液滴之间的相互作用
液滴在折流板通道内流动过程十分复杂,液滴之间难免会发生不同类型碰撞.当庞大数量的液滴一起在折流板通道内流动时,每个液滴都可能与剩余的液滴碰撞.
O’rourke[11]提出了一种计算液滴碰撞时的算法,通过进行随机估计计算液滴碰撞概率能够有效的降低计算液滴碰撞的次数.因此,本文使用了O’rourke方法计算液滴发生碰撞的后续发展结果.
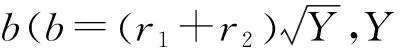
由文献[11]可知,临界偏移量bcrit的计算式为
(18)
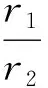
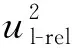
碰撞后由O’rourke法计算出碰撞后的速度表达式:
(21)
1.2.3壁面液膜形成及分离
液滴在喷入分离腔后流动状态复杂,在折流板内流速变化大.与欧拉壁膜模型相比,拉格朗日壁膜模型(LWF)通过瞬态的粒子将物理效应离散化,在特定的条件下模拟液滴与壁面碰撞形成液膜的过程,非常适合液滴在折流板内流动的快速瞬态效应.
在使用拉格朗日壁膜模型时,且不涉及传热问题时必须满足以下的假设及限制条件:液膜温度小于液体的沸点温度;壁面温度为300 K,即常壁温条件;液膜饱和温度为5 000 K;Re和We中的液滴速度垂直于壁面,数值上为液滴相对壁面的速度.
本文分析了常温环境的气液分离现象,液滴与壁面之间无热量交换,折流板壁面光滑且为润湿壁面,因此选用了Stanton-Rutland碰撞模型.
1) Stanton-Rutland撞击模型
在不同的壁面条件(壁面温度、干湿状态、粗糙度)和液滴的撞击条件(液滴直径、速度)下,液滴与壁面冲击后的结果也不同,如图2所示[12-13].根据文献[13]可知,临界壁面Tcrit= 1.0×5 000 K,临界无量纲能量Ecrit=57.7.本文的壁面温度为常壁温,远小于Tcrit值,因此液滴撞击壁面只可能发生飞溅、铺展、沉积三种可能的结果.若撞击壁面时的无量纲能量小于16,则液滴附着在折流板表面从而形成液膜;若无量纲能量大于16小于Ecrit时液滴在折流板表面附着后逐渐铺展开;若无量纲能量大于Ecrit时液滴撞击折流板壁面后在液膜表面飞溅出小的液滴,飞溅的液滴数本文采用fluent默认值4,而这些飞溅出去的小的液滴又会进入气流中继续流动.

图2 液滴撞击壁面时的相互作用决策图Fig.2 Interaction decision diagram of droplet impacting the wall
液滴撞击壁面时的能量定义式为
(22)
式中:uln为液滴垂直于壁面的速度分量,m/s;ρl为液滴密度,kg/m3;dl为液滴直径,m;σ为液滴的表面张力,N/m;h0为在壁面形成的液膜厚度,m;δbl为边界层厚度,m.
2) 液滴在壁面边缘分离模型
当折流板两壁面间的夹角及薄膜流动的惯性足够大时,粘附在壁面的壁膜有可能剥离出液滴.O’rourke边缘分离模型假设剥离出的液滴直径等于边缘处薄膜的高度,其质量流率等于流过边缘的薄膜的质量流率,从而计算了从壁膜分离出的液滴的直径和质量流率.
第一,如果所学内容涉及到运算律,但授课的时间在学运算律之前,例如“凑十法”本质上是加法结合律,老师们不能使用运算律的知识,但在讲运算律的时候,前面的知识可以作为使用运算律的例子,让学生充分感受到运算律的应用是十分普遍的.
壁膜剥离出液滴的条件为
(23)
式中:γ为液滴从壁面分离时的分离角;Wef为液滴发生分离时的韦伯数,定义为
(24)
式中:σ为膜的表面张力,N/m.本文数值中,折流板叶片左侧壁面的分离角为117°,右侧叶片壁面的分离角为63°.临界韦伯数Wec为0.
3) 液滴剥离模型
基于Bertodano等[14]和Mayer[15]的工作,提出液滴剥离模型.当空气与壁面上的液膜之间存在较大的相对速度时,在足够高的气流剪切速率下,会在壁膜表面形成开尔文-亥姆霍兹波.如Mayer所述,处于剪切流里的薄的液膜会产生波长为λ的开尔文-赫姆霍兹波,这种波会自发增长并在一定的条件下最终从薄膜中剥离出液滴.
从薄膜中剥离出液滴必须满足波的频率ω必须大于零,ω可表示为
(25)
ω大于0可以推导出最小波长λmin应满足:
(26)
式(26)中f和v的计算式分别为
Bertodano等[14]提出波的频率ω也可以利用泰勒理论的线性稳定性分析获得
(29)
由文献[14]可知,从液膜中剥离出的液滴平均直径可通过式(30)获得
(30)
式中:数值因子F的默认值为0.14.
(31)
式中:C默认值为0.5.
由此得到了从开尔文-赫姆霍兹波中剥离出的液滴直径及质量流率.
1.3 边界条件
采用DPM模型模拟折流板内液滴的运动情况.通过随机轨道模型求解液滴受到气流的湍流效应而引起的湍流扩散.对连续相流场进行求解,建立离散相的喷射源、定义液滴初始外置、速度、喷射时间等初始条件,边界条件设置具体如表3所列.

表3 具体边界条件设置
1.4 分离性能评价指标
折流板的分离性能主要是指在不同工况下对于液滴的分离性能,主要包括分离效率ηp和压降ΔP两个评价指标.分离效率由式(32,33)表示:
式中:Qin和Qout分别为进出口液滴质量流率,kg/s;Pin和Pout分别为折流板进出口压力,Pa.
2 网格无关性及模型验证
2.1 网格无关性验证
采用结构化网格对计算区域进行划分,为提高计算精度,并在壁面处进行边界层的加密处理.分别选取网格数量为8 640、19 165、52 563、75 436四套网格,如图3所示.综合考虑计算效率和计算精度,经过大量试算发现网格数量为19 165时满足计算要求.

图3 折流板局部网格分布Fig.3 Local grid distribution of the deflector
2.2 模型验证
为了验证模拟结果的可靠性,将折流板数值模拟的计算值与试验测量值进行对比.由于试验条件的限制,选取与折线形折流板原理相同的水平梯形折流板为试验对象,分析了其数值模拟计算结果与试验测量数据的对比结果,如图4所示.可以看出,数值模拟的分离效率曲线与试验结果十分接近,而数值模拟的压降较实验测得压降高30 Pa左右.这是因为在试验过程中,空气从气体管路进入分离腔的过程中压力有一定的损失,造成进入分离腔时压力降低,所以流体经过折流板前后的压力差会有所降低;且在数值模拟时模型的简化一定程度上也会与试验情况存在差异,但模拟结果与试验结果误差在可接受范围内,可以认为数值模型可靠性较高.

图4 模拟可靠性验证
3 结果分析与讨论
3.1 折流板内部流场分析及分离性能评价
通过分析折流板内的压降特性及流场情况,可以有效地改善折流板的分离性能.因此,对环境温度为常温、入口气流速度为1.5 m/s、板间距W=20 mm、叶片转折角θ=50°的工况下,折流板通道内流场情况进行了分析.图5a为折流板内气相速度场云图,从图中可以看出流体进入折流板通道后被叶片右侧壁面阻挡,气流向下偏转,速度增大,最大可达到3.8 m/s左右.图5b为对应的气相压力云图,可以看出,压力在每级叶片后都会有明显的分区现象,气流在进入折流板时压力最高,随着流动过程中叶片的阻碍作用,压力开始逐级降低.但每级叶片的右侧内壁面都出现了局部压力增大的情况,这是因为流体在顺着折流板通道进入叶片后被右侧的壁面拦截,使得气流在此区域暂时聚集而引起压力增大.此后,随着流动过程中的能量损失,这种现象变得不再明显.
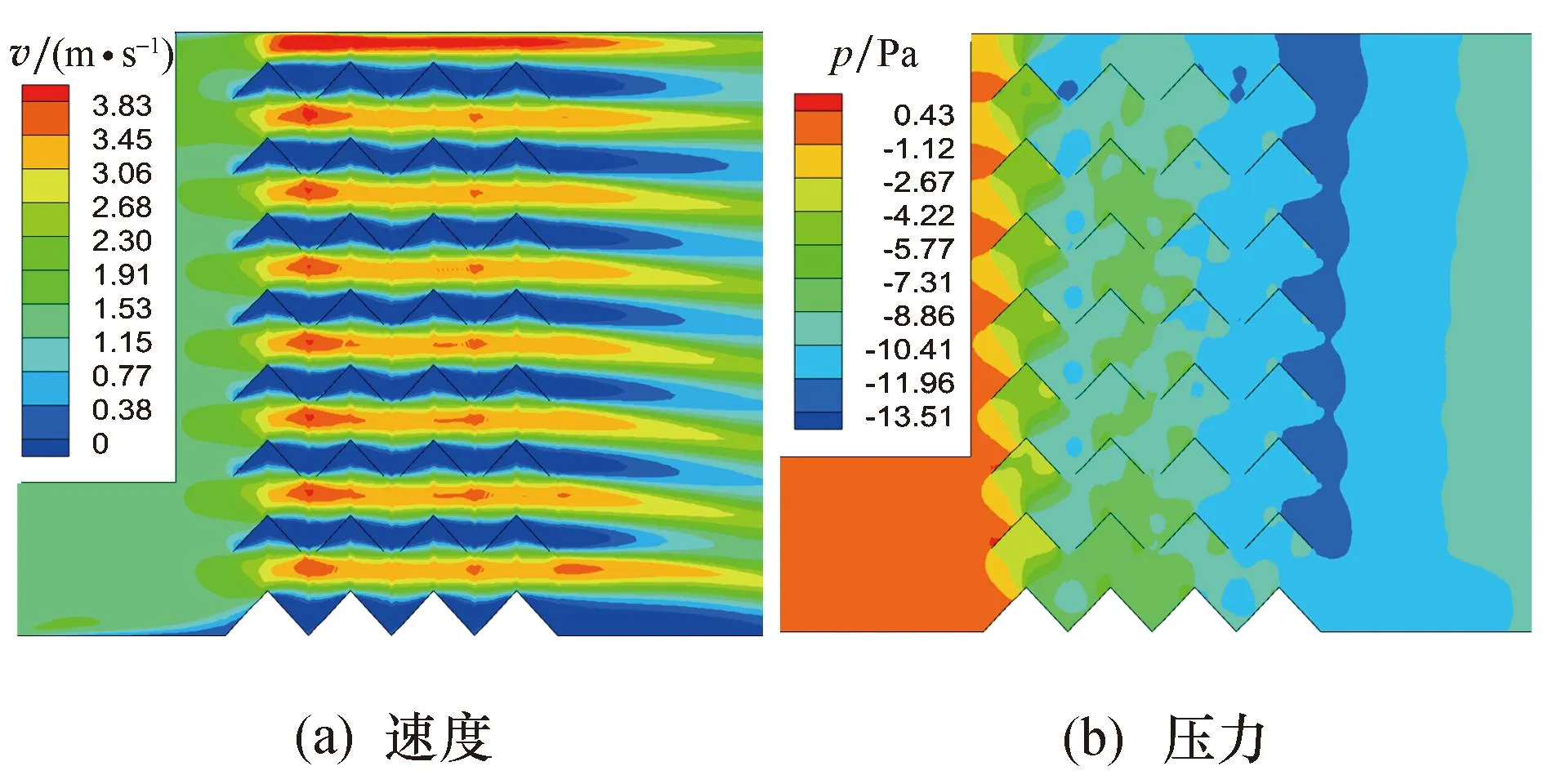
图5 入口流速为1.5 m/s时流体速度和流体压力分布Fig.5 Fluid velocity and pressure distribution when the inlet velocity is 1.5 m/s
3.2 入口流速对分离特性的影响规律
研究板间距W=20 mm、叶片转折角θ=50°的工况下,入口流速对分离性能的影响规律,如图6所示.从图中可以看出,分离效率呈对数函数形式,即其随着入口流速的增大而逐渐增大,最终趋近于水平.这主要与液滴碰撞叶片壁面后的后续发展有关,当液滴与倾斜壁面发生碰撞后会经历五个阶段:动力学阶段、铺展阶段、滑动阶段、回缩阶段和稳定润湿阶段.由于动力学阶段历时非常短(10-6ms),可忽略.在铺展阶段,液滴与壁面碰撞后沿着其径向方向在壁面延展开来,此时液滴所具有的原始动能开始转化为表面能、内能和液滴内部流体的动能,液滴的铺展直径持续增大直到最大值并且呈薄饼形状.随着气流速度增大,此时液滴所具有的原始动量增加,液滴在叶片壁面的聚合加快,使得从叶片表面滑落的液滴直径更大,因此不易被气流携带再次进入流体通道内,分离效率有所升高.同时,还能观察到压降随着流速的增大而增大.

图6 不同入口流速下分离效率及压降特性曲线Fig.6 Characteristic curves of separation efficiency and pressure drop for different inlet flow rates
图7为不同入口流速时折流板内流场速度矢量图,对比发现随着气流速度的增加,流场内的最大速度也增加.此外,随着入口流速的增加,在叶片及两叶片之间的凹槽壁面区域流速也较大,使得在此区域内生成的涡旋减少,气流被迫从排液孔流出,增加了流动阻力,因此流体在流经折流板后压降增大.

图7 不同入口速度的流场速度矢量图
总体而言,在一定程度上,随着入口流速的增大,分离效率会逐渐增大.因此在折流板运行期间,适当增大流速可提高分离效率.
3.3 液滴尺寸对分离特性的影响规律
研究板间距W=20 mm、叶片转折角θ=50°、入口流速Vd0=7.5 m/s的工况下,液滴尺寸对分离性能的影响规律.图8为不同液滴尺寸下分离效率及压降特性曲线.从分离效率曲线可以看出,液滴直径小于130 μm时,分离效率略微降低;液滴直径大于130 μm后,分离效率逐渐增大.这是因为在入口流速一定时,当液滴直径较小时,液滴具有的初始动能较小,液滴在叶片上表面形成的液膜顺着叶片壁面滑落后,再次被气流携带走,造成分离效率的下降;当液滴直径大于130 μm后,液滴所具有的原始动量增加,液滴在叶片壁面的聚合加快,使得从叶片表面滑落的液滴直径更大,因此不易被气流携带再次进入流体通道内,分离效率有所升高.从压降曲线可以看出,随着液滴尺寸的增大,压降整体变化很小.

图8 不同液滴尺寸下分离效率及压降特性曲线Fig.8 Characteristic curves of separation efficiency and pressure drop for different droplet sizes
图9为不同液滴尺寸下折流板内湍动能分布,从中可以看出,随着液滴尺寸的增加,折流板内流动状态十分接近,湍动能几乎没有发生变化,故压降整体变化较小.

图9 不同液滴尺寸下湍动能分布云图Fig.9 Distribution diagram of turbulent kinetic energy for different droplet sizes
综上所述,液滴尺寸小于130 μm时,随着液滴尺寸的增大,分离效率会缓慢减小;液滴尺寸大于130 μm时,随着液滴尺寸的增大,分离效率会逐渐增大.因此,在此叶片结构下的入口液滴尺寸应在合理范围内尽量增大.总体而言,液滴尺寸对压降影响较小.
4 结论
基于DPM与拉格朗日液膜模型,建立了折线型折流板间隙内气液流动分析模型,模拟研究了折流板运行参数对分离性能的影响规律,得出了以下结论:
1) 在环境温度为常温、入口气流速度为1.5 m/s、板间距W=20 mm、叶片转折角θ=50°的工况下,气流进入折流板通道后会被叶片右侧壁面阻挡,向下偏转,导致速度增大.压力在每级叶片后都会有明显的分区现象,折流板入口处压力最高,由于流动过程中叶片的阻碍作用,压力开始逐级降低.但每级叶片的右侧内壁面都出现了局部压力增大的情况.
2) 在一定程度上,随着入口流速的增大,分离效率会逐渐增大.因此在气液分离设备运行期间,适当增大折流板入口流速可提高分离效率.但压降会随之增大,提高系统能耗.
3) 液滴尺寸小于130 μm时,随着液滴尺寸的增大,分离效率会缓慢减小;液滴尺寸大于130 μm时,随着液滴尺寸的增大,分离效率会逐渐增大.因此,在此叶片结构下的入口液滴尺寸可在合理范围内尽量增大以提高分离效率.总体而言,液滴尺寸对压降影响较小.

