四元数矩阵方程最小二乘Toeplitz解的半张量积方法

闫立梅, 赵琳琳, 丁文旭, 李 莹, 范洪彪

(1. 德州学院 数学与大数据学院, 山东 德州 253000; 2. 聊城大学 数学科学学院, 山东 聊城 252000)

为了克服普通矩阵乘法受维数的限制,程代展等[1-2]提出了矩阵的半张量积理论,矩阵的半张量积是矩阵普通乘法的推广和延展.该理论一经提出,在与矩阵有关的诸多领域得到了广泛应用.Fan等[3]和Cheng等[4]提出了求解模糊关系方程的半张量积方法,给出了模糊关系方程有解的充分必要条件,找到了所研究模糊关系方程全部的精确解;Fu等[5]使用矩阵的半张量积方法研究了有限Boolean代数的分解以及同构和同态问题;Cheng等[6]使用半张量积方法讨论了多值逻辑的完备性问题;葛美侠等[7]在半张量积的理论框架下研究了网络演化博弈,给出了网络演化博弈策略一致性的充要条件;丁文旭等[8],王栋等[9]和Ding等[10]将半张量积理论用于求解四元数矩阵方程,提出了四元数矩阵的实向量表示方法,得到了较好的效果;半张量积理论在其它领域也得到了成功的应用[11-13].

本文使用矩阵的半张量积方法研究四元数线性系统(1)的最小二乘Toeplitz型矩阵解和Hermitian Toeplitz型矩阵解.

(1)

Toeplitz矩阵在超视距雷达[14]、噪音消除[15]、计算机视觉[16]等工程应用领域发挥着重要的作用,是矩阵理论的研究内容之一.

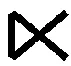
1 预备知识

定义1[17]设x1,x2,x3,x4∈R,称

x=x1+x2i+x3j+x4k

为四元数.其中,i,j,k满足i2=j2=k2=ijk=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j.

定义2设X∈Qn×n,称

为四元数Toeplitz矩阵.显然,四元数Toeplitz矩阵由它的第一行和第一列上共2n-1个元素决定.

定义3[1-2]设A∈Rm×n,B∈Rp×q,t=lcm(n,p)是n和p的最小公倍数,称

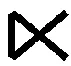
为A和B的矩阵半张量积.

矩阵半张量积一般不具有交换性.但可以在换位矩阵的协助下具有一定的交换性,称之为准交换性.

定义4[1-2]称

故有,

简记为

W[m,n]=δmn[1,…,(n-1)m+1,…,m,…,mn]

换位矩阵可以起到交换两个行向量和列向量相乘顺序的作用.

性质1[1-2]设x∈Rm,y∈Rn,A∈Rp×q,则

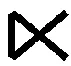
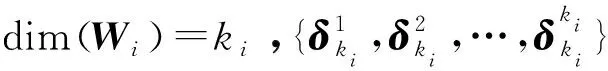
ij=1,2,…,kj;j=1,2,…,n

设

称MF为F的结构矩阵.

定义6[8]设四元数x=x1+x2i+x3j+x4k,称vR(x)=(x1,x2,x3,x4)T为x的实排列.

设x,y∈Q,xy的实排列vR(xy)可以通过半张量积方法用实向量vR(x),vR(y)来表示.

引理1[1-2]设x,y∈Q,则

其中

为两个四元数乘积的结构矩阵.

丁文旭等[8]提出了四元数行向量和列向量的实排列以及四元数矩阵的实行排和实列排概念.

定义7[8]设x=(x1,x2,…,xn)为四元数行向量,y=(y1,y2,…,yn)T为四元数列向量,称

分别为四元数向量x和y的实排列,vR(x),vR(y)∈R4n.

定义8[8]设A∈Qm×n,Rowi(A),Colj(A),i=1,2,…,m;j=1,2,…,n分别是A的第i行和第j列,称

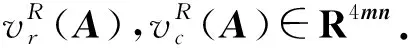
四元数向量和四元数矩阵的实向量表示具有下面的性质.

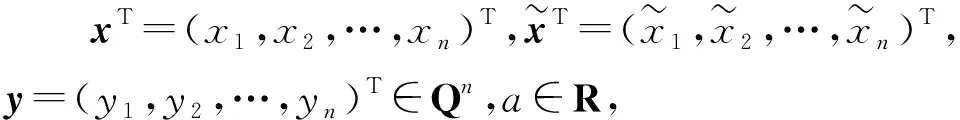
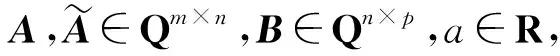
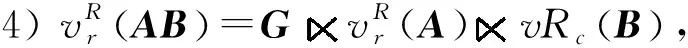
R4mp×16mn2p

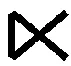
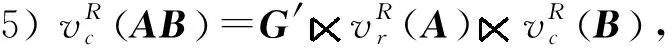
引理4[18]设A∈Rm×n,b∈Rm,则不相容线性方程组Ax=b的最小二乘解的通式为x=A+b+(In-A+A)y,其中y∈Rn是任意的向量.

引理5[18]设A∈Rm×n,b∈Rm,则线性方程组Ax=b有解的充分必要条件是AA+b=b,且其通解为x=A+b+(In-A+A)y,其中y∈Rn是任意的向量.

2 方程(1)的最小二乘Toeplitz解和Hermitian Toeplitz解

称XT为四元数矩阵方程(1)的极小范数最小二乘Toeplitz解.

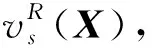
定理1设X∈TQn×n,且

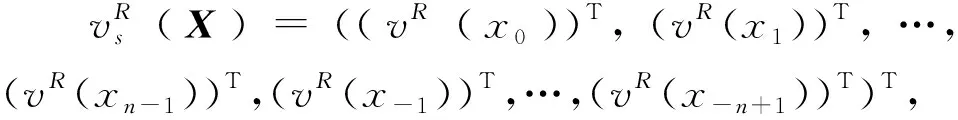
定理2设Xi∈TQn×n,i=1,2,…,k,记

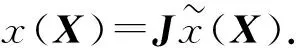
定理3设Ai∈Qm×n,Bi∈Qn×p,i=1,2,…,k,C∈Qm×p,则四元数矩阵方程(1)的最小二乘Toeplitz解为

其极小范数最小二乘Toeplitz解XT满足:

(2)

式中

G′与G在引理3中已交待(其维数不同), 矩阵J如定理2 中所示.

证明由引理2、引理3和定理2 可得

则

y∈R4k(2n-1)

其极小范数最小二乘Toeplitz解XT满足:

推论1设Ai∈Qm×n,Bi∈Qn×p,i=1,2,…,k,C∈Qm×p,四元数矩阵方程(1)有解的充要条件:

其通解为

y∈R4k(2n-1)

其极小范数Toeplitz解XT满足:

证明

因此,

y∈R4k(2n-1)

其极小范数Toeplitz解XT满足:

问题2设Ai∈Qm×n,Bi∈Qn×p,i=1,2,…,k,C∈Qm×p且

欲求XHT∈SHT,满足:

称XHT为四元数矩阵方程(1)的极小范数最小二乘Hermitian Toeplitz解.

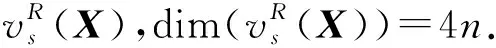
定理4设X∈HTQn×n,记

则

其中

定理5设Xi∈HTQn×n,i=1,2,…,k,记

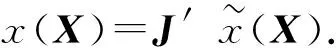
问题2与问题1的不同在于解的取值范围是不同的,仿照定理3与推论1给出四元数矩阵方程(1)的最小二乘Hermitian Toeplitz解的结论.

定理6设Ai∈Qm×n,Bi∈Qn×p,i=1,2,…,k,C∈Qm×p,则四元数矩阵方程(1)的最小二乘Hermitian Toeplitz解为

其极小范数最小二乘Hermitian Toeplitz解XHT满足:

(3)

推论2设Ai∈Qm×n,Bi∈Qn×p,i=1,2,…,k,C∈Qm×p,四元数矩阵方程(1)有解的充要条件是

其通解为

y∈R4kn

其极小范数Hermitian Toeplitz解XHT满足:

3 数值实验分析

算法

步骤1 输入矩阵Ai∈Qm×n,Bi∈Qn×p,i=1,2,…,k,C∈Qm×p,G′,G,W[4np,4n2],J;

步骤2 计算

下面的算例验证了该算法在求解四元数矩阵方程Toeplitz解时的精度和有效性.

算例1针对不同维数的四元数矩阵方程(1),检验上述算法的精度.取k=2,随机生成四元数矩阵,

Ai=rand(m,n)+rand(m,n)i+ rand(m,n)j+rand(m,n)ki=1,2

Bi=rand(n,p)+rand(n,p)i+ rand(n,p)j+rand(n,p)ki=1,2

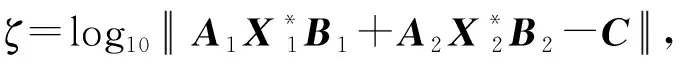
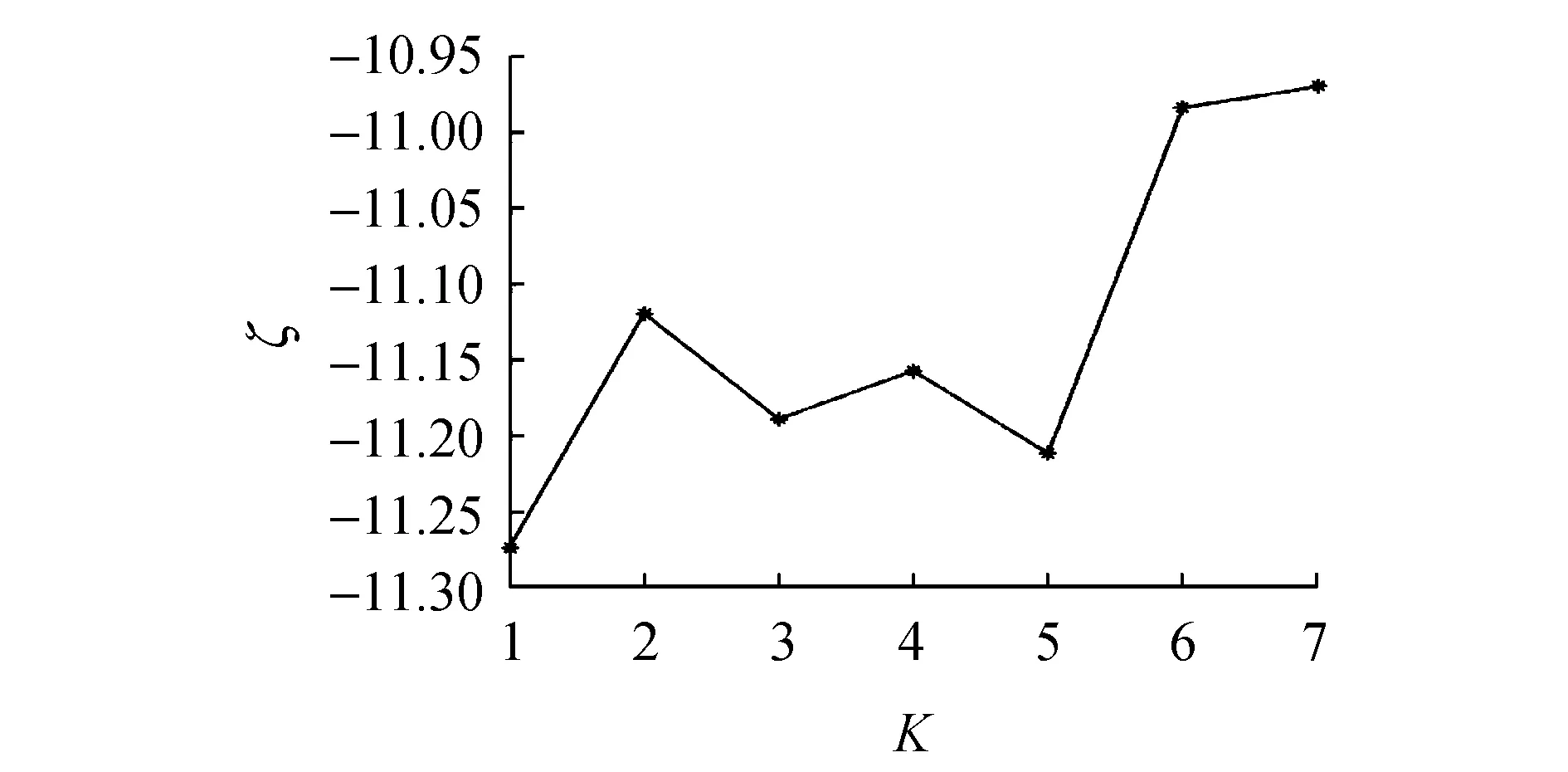
图1 矩阵不同维数下的误差ζFig.1 Errors ζ under different dimensions of matrix

4 结论

同时考虑矩阵的半张量积理论和四元数矩阵的实向量表示方法,构建了求解四元数矩阵方程的最小二乘Toeplitz解和Hermitian Toeplitz解的半张量积方法.针对解矩阵的特殊结构,提取有效消息去除冗余,降低了计算复杂度,提高了运算精度.这种方法可以推广使用求解其它的四元数矩阵方程,是一种求解四元数矩阵方程特殊形式解的有效方法.