善用回归策略，提升数学解题能力

夏世中

摘要：在九年级紧张的复习阶段，教师若善用回归策略，紧扣数学本质，能引导学生在茫茫题海的探寻中让数学知识得以巩固，在追根溯源中让数学理论得以归真，在解题总结和反思中让数学思想与方法得以彰显，从而有效提升解题能力.

关键词：复习；回归；原型；数学思想与方法

在九年级复习阶段，尤其在各类考试之前，许多学生都会陷入题海无法自拔，只重视解题的数量而忽视解题的质量，只重视解题的结果而忽视解题的过程，只忙于解题而忽视解题后的反思，尤其是对于题中考查的知识点、数学思想方法等数学本质方面的思考几乎为零.这种为了解题而解题的做法不仅消耗了学生大量的精力，浪费了宝贵的时间，而且复习效果甚微，也在一定程度上制约着学生解题能力的提高.

那么，结合九年级复习的特点，如何有效解题才能更好地提升复习的效果和学生解题能力呢？笔者认为，回归策略是一种行之有效的策略.九年级的复习是一个庞大的系统，在复习中，要让学生回归数学本质，如回归基础知识、基本原型、基本思想与方法等，并以此指导解题，在解题之后进一步反思，以促进对知识的理解和内化，形成数学观念，提升解题的思维能力.从数学的本质特征来说，可以把回归的方法细分为回归定义、回归基本原型、回归数学思想与方法三种，下面具体谈谈每种方法的应用.

1 回归定义

概念是构成学科的基石，定义是对一个概念的内涵和外延所作的简要而准确的描述，反映了知识点的本质属性.“回归定义”实质是以定义为核心知识点，用定义的本质来解决数学问题的方法，是一种朴素又重要的回归方法.核心概念、重要定义向来都是中考试题的重要考点，在突出考查数学的本质与基础的同时，也引导着教与学要回归本源，重视对基础知识和基本技能的夯实.

例1 （2020湖北黄冈中考试题）甲、乙、丙、丁四位同学五次数学测验成绩统计如表1所示，如果从这四位同学中，选出一位同学参加数学竞赛.那么应选（）去.

A.甲 B.乙 C.丙 D.丁

分析：本题主要考查平均数、方差的定义.先看平均数，平均数大的同学其成绩相对较好，若平均数相同，则选择方差小的同学.方差是反映一组数据的波动大小的量.方差越大，则数据与平均值的离散程度越大，稳定性也越小；反之，方差越小，数据与其平均值的离散程度越小，稳定性也越好.所以乙的成绩好且稳定.故选：B.

概念和定义是数学本质的根本，熟练掌握它们的内涵与外延，是深入理解数学本质的基础，是起决定性作用的第一步，因此教师要予以重视并引导学生进行灵活运用.

2 回归基本原型

著名数学家华罗庚曾经说过，对于复杂的问题要善于退，直到退到不能再退为止，再从此出发向前推进.九年级的复习中，有大量的综合题型，对于这类复杂的数学问题，要化繁为简，化未知为已知，找出其中的原型.当然回归原型，不光可以把复杂的问题转化为基本问题，也可以是把复杂的图形转化为基本图形，还可以是把复杂的方法转化为基本的方法.这样一个拨云去雾溯根源的过程有利于我们深入理解数学问题，抓住数学本质，达到解一题通一类的复习效果.

例2 （2022年武汉市中考题）如图1，在Rt△ABC中，∠ACB=90°，AC>BC，分别以△ABC的三边为边向外作三个正形ABHL，ACDE，BCFG，连接DF.过点C作AB的垂线CJ，垂足为J.分别交DF，LH于点I，K.若CI=5，CJ=4，则四边形AJKL的面积是___________.

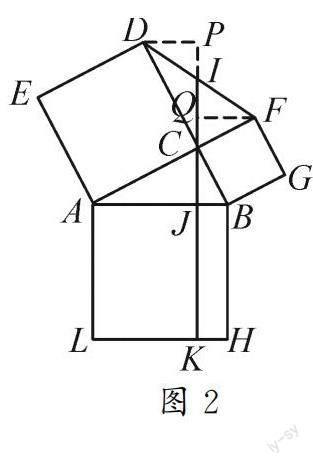
分析：如图2，过点D作DP⊥CI，交CI的延长线于点P，过点F作FQ⊥CI于点Q.通过作两条垂线，构造两组全等三角形△ACJ≌△CDP（AAS）和△BCJ≌△CFQ（AAS）.因此借助全等三角形实现线段长度关系的转移，AJ=CP，DP=CJ=4，BJ=CQ，QF=CJ=4，所以DP=QF，从而△DPI≌△FQI（AAS），所以DI=FI，PI=QI.因为∠DCF=90°，所以DI=FI=CI=5.

在Rt△DPI中，由勾股定理可得PI=3，所以QI=PI=3，于是AJ=CP=CI+PI=5+3=8，从而BJ=CQ=CI-QI=5-3=2，则AB=AJ+BJ=8+2=10.因为四边形ABHL为正方形，所以AL=AB=10.又四边形AJKL为矩形，故四边形AJKL的面积为AL·AJ=80.

由图2可以总结出以下几个结论：（1）S_△ABC=S_△DFC；（2）若IJ⊥AB，则DI=FI，AB=2CI；（3）若DI=FI，则IJ⊥AB，AB=2CI.回归到以往的解题经验，发现这类几何图形还有其他的形态.如图3，把两个正方形换成两个等腰直角三角形；如图4，把两个正方形换成两个相似直角三角形；等等.它们的相关结论也是成立的.

多组相似的几何图形必然是由某个原始的几何模型衍生和变形得到的，通过寻根溯源，我们发现这一模型来源于七世纪印度数学家婆罗摩笈多（Brahmagupta）的一个定理：如果一个圆内接四边形的对角线互相垂直相交，那么从交点向某一边所引垂线的反向延长线必经过这条边对边的中点.由该定理衍生了一系列的几何图形，其模型的结论当然都成立.至此，学生豁然开朗.尽管图形有着七十二变的魔力，但是总也逃不出我们的掌心，我们有复原它的能力，让其回归本真，各个击破.

3 回歸数学思想与方法

虽然九年级的复习内容多而杂，但是众多的内容所反映出的数学思想与方法却十分有限.比如，在初中阶段由一次函数、二次函数、正比例函数、反比例函数的概念和性质所提炼出的思想都叫做函数思想，方程知识对应的是方程思想，几何与代数的有机结合形成数形结合思想.这些思想是对数学知识本质的概括和浓缩，而数学方法是数学思想的具体反映，如整体思想中体现了换元法.这些数学思想与方法是数学学习的精髓，是解题的金钥匙.在解题教学中回归数学思想与方法的渗透，是提升学生解题能力的关键，也是培养能力、发展思维的重要途径，甚至影响着学生以后的数学学习与知识的应用能力.

例3 反比例函数y=k/x（x＞0）过点A（3，4），直线AC与x轴交于点C（6，0），过点C作x轴的垂线BC交反比例函数图象于点B.

（1）求k的值与点B的坐标；

（2）在平面内有点D，使得以A，B，C，D四点为顶点的四边形为平行四边形，试写出符合条件的所有点D的坐标.

分析：第（1）问以函数思想来指导解题，具体体现在用待定系数法求k的值，求出k=12，点B的坐标是（6，2）.

第（2）问，若以A，B，C，D四点为顶点的四边形为平行四边形，则需在已知A（3，4），B（6，2），C（6，0）的前提下求点D.由于平行四边形的形状具有不确定性，因此需要分类讨论，所以以分类讨论思想为指导来解题.

不妨以AC为平行四边形的边还是对角线为分类标准进行分类讨论.

①当AC为对角线时，如图5，AD∥BC，且AD=BC，建立关系，列方程y_A-y_D=y_B-y_C，求得D（3，2）.

②当AC为一边时，如图5，当四边形ACBD′为平行四边形时，AD′∥CB且AD′=CB.

建立关系，列方程y_D′-y_A=y_B-y_C，求得点D′（3，6）.

③当AC为一边时，如图5，当四边形ACD″B为平行四边形时，AC=BD″且AC=BD″.

建立关系，列方程x_D″-x_B=x_C-x_A，y_D″-y_B=y_C-y_A，求得D″（9，-2）.

综上所述，符合条件的点D的坐标是（3，2）或（3，6）或（9，-2）.

这是一道反比例函数与平行四边形的综合题，以此题为载体，在讲解时以函数思想、方程思想和分类讨论思想、数形结合思想为统领，指导学生如何一步步运用所学数学知识解题.在融会贯通平行四边形的性质、判定等知识的同时，也让学生理解蕴含在其中的思想方法，以及思想方法对解题的指导作用.

九年级的复习资料堆积如山，唯有把握其中的数学本质，才能把资料从厚变薄，把所学的知识系统化、条理化.九年级的题型千变万化，题设条件错综复杂，唯有紧扣数学的本质，才能随機应变，轻松应对.回归定义、基本原型、数学思想与方法正是回归数学本质的具体方法.这种由表及里、循序渐进、步步深入的解题方式，能帮助学生寻觅到解题的门道，寻求到通解与通法，以不变应万变，从而脱离茫茫题海，体验成功解题的乐趣，实现数学能力的有效提升，也无形中增强了学生备战中考的信心.