法尼亚诺关于双纽线弧长测量问题的研究

张巧艳，刘 茜

（西北大学 科学史高等研究院，陕西 西安 710127）

17 世纪后期，牛顿和莱布尼茨创建了比较系统的微积分[1]。积分没有独立的定义，它是作为微分的逆运算而存在的。微积分能处理各种特殊问题：求速度、做切线、求极大极小值、曲线在某点的曲率等问题可统一用微分法来解，而求曲线弧长、面积、体积、重心、距离等问题可用积分来解[2]。

当时对于曲线求弧长问题极难求解，包括椭圆与双曲线的弧长问题，除了直线、圆及抛物线之外，第一个求得绝对弧长的曲线就是“半立方抛物线”y2=ax3。1657 年英国数学家耐尔（William Neil，1637—1670）求出了它的弧长。1670 年，牛顿在《级数与流数方法论》中也求出了半立方抛物线的弧长，他知道一般的求弧长公式，但在求椭圆弧长时，只是得到了无穷展开的级数[2]。

1694年雅各布·伯努利（Jakob Bernoulli，1654—1705）和约翰·伯努利（Johann Bernoulli，1667—1748）相继研究了双纽线的构造问题。雅各布·伯努利用弹性曲线性质来解决莱布尼茨在1689年提出的等时线问题，他得到微分方程，并对其进行积分，等式右边就是曲线的弧元。然而，这并不完全令人满意，因为它要求对等时线问题的解依赖于超越曲线，而超越曲线的方程只能通过对物体的弹性作假设来建立。因此，雅各布·伯努利提出了另一种等时线的构造，使用了一种全新的曲线——双纽线（lemniscate），也称伯努利双纽线。它是一个代数曲线，而不是一个超越曲线。此外，约翰·伯努利也朝着同样的方向前进，他也在寻找一条能够修正旁心等时线的代数曲线。于是，伯努利兄弟以不同的方式得到了代数方程(x2+y2）2=a2(x2-y2)。它的形状（图1）是一个横置的“8”，或者像一个打结的花边，lemniscate 在法语中是一个丝带结。如果用θ表示弦CP和r表示∠RCP，则可得到极坐标的曲线方程为r2=a2cos（2θ）。在曲线上被半径圆截取的弧长用积分表示为。这很容易得到双纽线的弧长和弹性曲线的弧长相等。

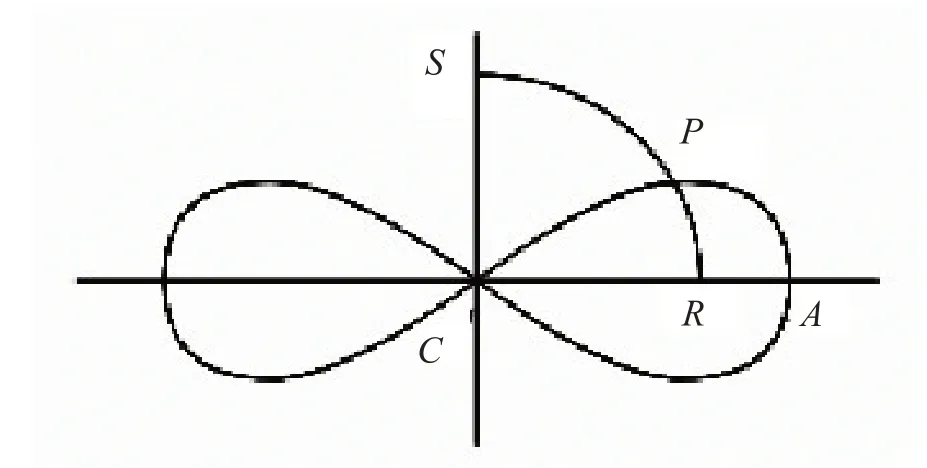
图1 双纽线构造示意图

1698年，约翰·伯努利发现绝大多数曲线的弧长并不能用初等函数表示，但是这些曲线的弧长的和或差有可能可以用初等函数表示。他发现立方抛物线y=x3的两段弧长的差是可积的，然后将这一结果推广到一些高阶抛物线、椭圆和双曲线弧长的更一般问题上，但是他没有给出证明[1]。

17世纪到18世纪，关于椭圆积分处理有三大类问题：（1）微分方程的几何构造。当处理包含椭圆微分方程时，很自然地寻求用更简单的曲线——圆锥截面进行求积构造。（2）不同曲线弧线的比较。通过修正或正交构造，将所研究的曲线的圆弧与圆锥截面的圆弧进行比较，当这些曲线与圆锥之间存在几何关系时，将前者的测量与后者的测量进行比较。（3）同一曲线的弧的比较。曲线的测量不是修正或变换到椭圆（双曲线）的弧，而是曲线本身的测量。第三类问题涉及将同一条曲线的不同弧线相互联系起来，这些弧线可以从曲线的不同点去测量[3]。

1714 年，意大利数学家法尼亚诺（Giulio Carlo Fagnano dei Toschi，1682—1766）开始研究双纽线相关的问题。他试图在前人工作的基础上，通过研究双纽线弧长的测量方法来求解积分，他的工作为整个椭圆积分的建立做出了重要贡献[2]。目前有关法尼亚诺关于双纽线的工作的研究文献主要有莱姆德（Raymond）的《法尼亚诺关于双纽线椭圆积分的贡献》[4]、斯瑞得哈（Sridharan）的《从弹性曲线到双纽线》[5]以及周瑞宏的《法尼亚诺对椭圆积分的开创性贡献》[6]等。这些工作主要是对双纽线产生的历史、曲线性质以及在不同坐标系下曲线表达式之间的相互转换、双纽线倍弧长公式中的代数关系等的讨论，鲜少关注法尼亚诺用两种不同的双纽线弧长测量方法求解双纽线积分以及成功得出双纽线倍弧长公式的具体细节和原因。本文基于法尼亚诺1715 年至1718 年关于双纽线的论文[7-11]，在“为什么数学”的研究范式下[12]，结合几何图示对法尼亚诺双纽线的弧长测量方法以及双纽线倍弧长公式发现过程进行剖析，这不仅有助于更清楚直观地了解法尼亚诺在双纽线弧长方面的工作，而且有助于全面了解椭圆积分的历史发展过程。

1 基于圆锥曲线性质的双纽线弧长的测量

1718年，法尼亚诺发表了两篇题为《测量双纽线弧长的方法》[9-10]的论文。在第一篇论文中，他尝试利用椭圆和双曲线的性质去测量双纽线的弧长。在第二篇论文中，他首先用抛物线及其切线的性质再次尝试测量双纽线的弧长，其次利用等分第一象限双纽线弧长的方法去测量其弧长。

当双纽线半轴、椭圆曲线的短半轴和双曲线的半轴相等时，且椭圆曲线不定弦与双纽线不定弦取相同的值，可以找到第一象限与双纽线不定弦相对应的正向弧与反向弧的积分表达式，这个表达式每一项都分别对应于椭圆曲线与双曲线中的元素。这时将双纽线正向弧与反向弧相加便是第一象限的弧长，再将其乘以4，便是整段双纽线的弧长，通过适当的化简便可得出等式的右边为三项表达式之和，第一项是椭圆曲线弧长表达式，第二项是双曲线的弧长表达式，第三项是关于半轴与曲线弦的代数关系式。

法尼亚诺用定理与推论将其过程进行展示推理：

推论1若双纽线的弦CQ=z与椭圆的横轴CH=z，并且在双曲线LMP中，SO=t，并将其分别代入定理1中的等式中，则可推出

可见，由定理1 和推论1，他使得双纽线的弦与椭圆的弦相等并设为z（图2），双曲线的弦设为t（图3），并将其分别代入定理1 中的方程中，则推出了用椭圆弧和双曲线弧所替换出来的双纽线弧的表达式。

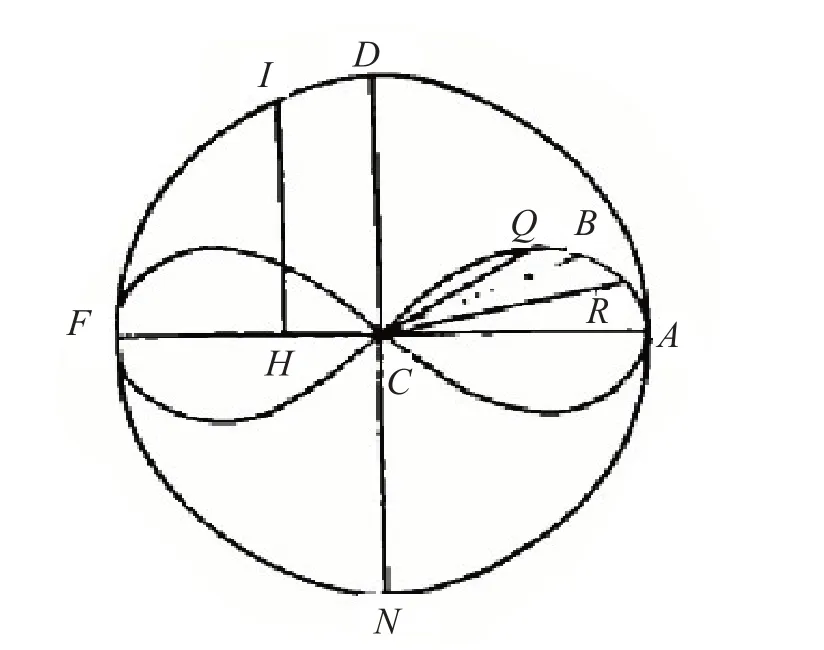
图2 椭圆和双纽线示意图（摘自法尼亚诺论文集附录插图24）

图3 双曲线示意图（摘自法尼亚诺论文集附录插图25）

推论2：若双纽线的弦CQ=z与椭圆的横轴CH=z，并且在双曲线LMP中，SL=r，并将其分别代入定理2中的等式中，则可推出

同样地，由定理2 和推论2，使双纽线的弦与椭圆的弦相等并设为z（图2），双曲线的弦设为r（图3），并将其分别代入定理2的等式中，则推出了用椭圆弧和双曲线弧所替换出来的另一段双纽线弧的表达式。

它是中国第一条以地方为主投资建设、技术标准最高的高速铁路，也是国家“八纵八横”高铁网中“一横”青岛至银川通道(青岛—济南—石家庄—太原—银川)的重要组成部分,是该通道的最东端一段,与该通道已经开通的石济高铁、石太高铁实现连通。济青高铁与胶济铁路、胶济客专在济南至青岛间形成“三线并行”的铁路交通运输格局,将极大提升济南至青岛间运输能力,对沟通山东省与三大经济带,推进国家级发展战略实施具有重要意义。

由式（2）（4），可推出双纽线的弧长为

即双纽线的弧长是可以用椭圆曲线弧与双曲线的弧及三者的轴长与弦长之间的代数表达式来替换的。

但是当z=a时，双曲线的SO将变得无穷大，使得弧也变得无穷大，因此似乎用这种方法测量双纽线的弧长遇到了困难。他在注释中也指出：“不能说是完美地发现了这条曲线的测量方法。”[9]法尼亚诺的尝试在取特殊值时无法用上述表达式来计算双纽线弧长。在第二篇关于双纽线的论文[10]中他尝试运用与第一篇相同的变换思想，进一步研究双纽线弧长的测量，利用双纽线的弦与抛物线曲线以及其某点处切线建立等式关系，利用这种弦与弧的对应关系去测量双纽线的弧长。

首先，法尼亚诺在论文[9]中展示了4个关于参数代换与其微分方程的定理，并对其赋予几何意义（图2）：

在双纽线中，法尼亚诺给出了每个弦所对应的正向弧与反向弧的积分表达式，而对应于抛物线他也给出了与割线所对应的弧长积分以及切线的表达式。通过定理3-6 中应用于曲线之间的代换，他展示将上述定理应用于几何中的示例，对定理中的微分方程进行积分，双纽线的每段弧长都可由右边的抛物线弧长与切线线性表示，他在注释中这样写道：

读者已经能使用前4 个定理来扩展抛物线来推导出测量双纽线的其他方法，在必要时会省去或添加适当的常数来完成方程。此外，他们能够从这些定理中推导出一些全新的真理，关于弧之间的比较等。我很高兴地提到，由于抛物线的大小在几个方面取决于前面4 个定理的双纽线的弧长，而双纽线的大小又取决于双曲线和椭圆曲线，因此抛物线的大小在几个方面又取决于上述两个曲线。[10]

因此，通过利用圆锥曲线弧长代换虽然没有真正测量出双纽线的弧长，但利用变换思想，法尼亚诺成功得到抛物线与椭圆和双曲线间的相互转换。

2 基于等分法的双纽线弧长的测量

法尼亚诺虽然没有成功利用圆锥曲线测量出双纽线弧长，但发现积分看起来非常相似，于是他想到类比圆弧的研究方法，将圆弧分割为任意等份，得到整个圆弧的长度。所以他便想到等分第一象限的双纽线并利用弦与弧之间的代数关系去寻找新的测量方法，这样或许可以测出双纽线的弧长。

在第一篇论文[9]后半部分，法尼亚诺研究了双纽线内部弦与弦的代数关系，以及弦所对应的弧之间的比较，成功将第一象限的双纽线弧长进行了二等分。

如图4 所示，结合定理7 及推论3，他发现，第一象限双纽线的两条不定弦若存在一个代数关系，则可使与第一条弦对应的正向弧与第二条弦对应的反向弧相等，只要使两条弦相等就可得到二等分弧。由此方法，他成功将第一象限双纽线的弧长进行了尺规减半。

图4 等分双纽线弧长示意图（摘自法尼亚诺论文集附录插图29）

对第一象限双纽线弧长的三等分以及五等分是在法尼亚诺第二篇论文[10]的后半部分，他依旧利用双纽线内部弦与弦的代数关系去分析。

如图4所示，为了方便代换，法尼亚诺将半轴的值a换为1，在二等分的基础上，他又找到第三条弦与第一条弦的代数关系，使得与第一条弦所对应的正向弧是第三条弦所对应的弧的2倍，依旧使第一条弦与第二条弦相等，这时就将第一象限的双纽线三等分了。

五等分第一象限双纽线弧则是结合了二等分弧以及三等分弧的方法：

法尼亚诺找到第四条弦与第三条弦之间的代数关系，使得与第三条弦对应的正向弧是第四条弦所对应的反向弧的2倍，这时便成功将第一象限的双纽线弧长进行了五等分。在找同时满足z和r的值时他写道：

这可通过定理8 和9 中的等式将字母z代替r来找到，从而推出，将u代入定理9 中，将产生另一个方程，除了z不包含其他未知数。如果假设z4=b，将产生一个新的八次方程。由于计算冗长，因此在本文中写下来是多余的。在表示z4 值的等式中，相同数量的z4 将有两个小于a4的真实值，这两个值中较大的表示CT(z)的平方，因为通过化解得到的是u而不是z，会发现与那个非常相似的等式。已故侯爵H.P 在他关于圆锥形截面论文lib9.rop9中教导了构造八次方程的方法。[8]93

以此类推，法尼亚诺还发现了将双纽线切割成给定数量的相等部分，再将每个部分分成两个相等部分的方法。虽然法尼亚诺已经知道如何将第一象限的双纽线弧长进行2×2m、3×2m、5×2m等分（其中m表示任意正整数）[10]，但他的等分是有限的，不能利用等分双纽线弧长的方法完全测出其弧长，故而也没有成功找到双纽线弧长积分的解。

3 倍弧长公式的发现

法尼亚诺的尝试虽未能如愿，但在此过程中他通过两个类似于正弦积分代换，成功得出了双纽线的倍弧长公式[14]。

这个替换没有使积分合理化，因为又得到了一个平方根；于是，他又做了第二次替换，设，则有

双纽线的倍弧长公式则为

1750年，法尼亚诺被提名成为柏林学院的成员，他的上述重要论文结集出版，总计1 000多页。1751年12月23日，法尼亚诺的论文集交由欧拉（Leonhard Euler，1707—1783）审阅，卡尔·雅可比（Carl Gustav Jacob Jacobi，1804—1851）称这一天为“椭圆函数理论的诞生之日”[16]。在法尼亚诺的众多论文中，发表于1718年的题为《测量双纽线弧长的方法》[9-10]的两篇论文引起欧拉的注意。1756—1757年，欧拉在《不可求长的曲线弧的比较研究》[17]一文中基于法尼亚诺关于双纽线的工作，在已经将双纽线的四分之一部分的面积n等分后，又考虑怎么将它n+1 等分。欧拉指出他和法尼亚诺的工作对积分提供了一些有用的结果。基于法尼亚诺的工作，欧拉在文献[18]中试图寻找微分方程的代数形式的通解。欧拉在椭圆积分相关主题上发表了数十篇论文，也正是在这些工作中发现了椭圆积分的加法公式。加法公式的发现对椭圆函数后来的发展产生了深远的影响[19]。

4 结语

在17 世纪至18 世纪关于椭圆积分处理的三大类问题中，法尼亚诺的研究是这些问题的一部分，他将其方法应用到了双纽线的研究中。在雅各布·伯努利和约翰·伯努利工作的基础上，法尼亚诺对椭圆积分的研究不仅具有明显的几何学倾向，还运用了代数与分析相结合的方式进行研究。在18世纪上半叶，法尼亚诺运用几何与代数以及分析的方法对椭圆积分的研究标志着构造几何逐渐在向分析方向延展。在1715—1718 年研究双纽线弧长时，他尝试利用微分方程的几何构造的方法寻求用更简单的曲线-圆锥截面测量双纽线的弧长。通过修正或正交构造，利用不同曲线弧线的比较将双纽线的弧与圆锥截面的弧进行比较，当这些曲线与圆锥之间存在几何关系时，将前者的测量与后者的测量进行比较。但由于在取到特殊值时无法测出双纽线的弧长，因此他便利用同一曲线的弧的比较去测量双纽线本身的弧长，并类比圆弧的测量方法，想到了等分双纽线弧长的方法，试图将第一象限的双纽线弧长进行无限等分得到整段弧长，进而求解积分。他成功将第一象限双纽线弧长进行了2×2m、3×2m、5×2m等分（其中m表示任意正整数），但他的等分是有限的，因此他的第二次尝试也没有成功，没有找到积分的解。幸运的是，他在这过程中发现了双纽线的倍弧长公式，这对于1751年欧拉发现椭圆积分的加法定理具有重要影响。而加法定理贯穿了整个椭圆函数理论，可以说法尼亚诺关于双纽线弧长的研究是椭圆函数理论的起点，他为椭圆函数理论的建立做出了重要贡献。