基于化学键偶极的精氨酸分子力场参数的建立
刘 琦, 祝佳怡, 姜笑楠, 孙长亮, 郝 强, 王长生
(1.辽宁师范大学 化学化工学院,辽宁 大连 116029; 2.沈阳化工大学 分析测试中心,辽宁 沈阳 110142)
在细胞代谢、信号传导以及基因表达等关键生命过程中,精氨酸显现出不可或缺的作用. 作为蛋白质的构建元素之一,精氨酸参与了蛋白质的构建,氨基酸及其衍生物的生物合成过程[1],同时也参与了尿素循环的调控[2]. 精氨酸在细胞质和细胞核内的生物合成过程中也具有重要的功能. 此外,精氨酸在胍基乙酸以及随后形成的肌酸合成过程中充当了重要的供体. 这种多重作用使得精氨酸成为维持蛋白质结构稳定性和功能活性的关键成分. 精氨酸在染色体包装、DNA修复以及其他细胞过程中的参与[3],使其备受生物学研究关注.
然而,精氨酸分子的复杂性远不止于其在生物学中的角色. 分子内和分子间的相互作用很大程度上受到其胍基上电荷分布和立体构型的影响. 这些电荷分布在精氨酸分子与其他分子之间的氢键、离子键以及范德华力等相互作用中扮演着至关重要的角色. 精确描述这些相互作用对于理解精氨酸在蛋白质结构的稳定性、酶活性以及其他生物学功能方面的作用至关重要[4].
分子力场方法作为分子模拟和计算化学领域的基石,为揭示生物分子的结构和相互作用提供了关键支持. 然而,现有的力场方法在涉及带电体系的精确描述方面仍存在限制. 特别是在描述如胍基上电荷分布这类复杂氨基酸的时候,现行的力场参数无法提供令人满意的结果. 因此,开发出适用于精氨酸分子的精准力场参数成为当前亟待解决的任务. 通过建立一个基于化学键偶极的精氨酸分子力场参数,将能够更加准确地模拟精氨酸胍基上电荷分布以及与其他分子间的相互作用,从而有助于更加深入地研究和理解生物分子中精氨酸的功能.
1 化学键偶极的分子力场方法
为了精确预测精氨酸分子,尤其是带电氨基酸侧链部分与水分子之间的相互作用,本文对质子化的精氨酸侧链与水分子组成的团簇体在NPT系综下进行2 ns的分子动力学模拟. 以轨迹中精氨酸侧链分子及其周围的两个水分子组成的复合物为基础,在B3LYP/6-31+G(d,p)水平下进行了结构优化. 以一个质子化的精氨酸侧链分子与两个水分子形成的复合物为研究对象,构建了一个包含15个稳定三体复合物(S1~S15)的训练集(如图1所示). 此外,还在考虑基组重叠误差校正的情况下,采用MP2方法结合aug-cc-pVTZ基组,获得了训练集中各构象的二体和三体相互作用能. 二体和三体相互作用能分别由式(1)、式(2)和式(3)、式(4)计算得到.
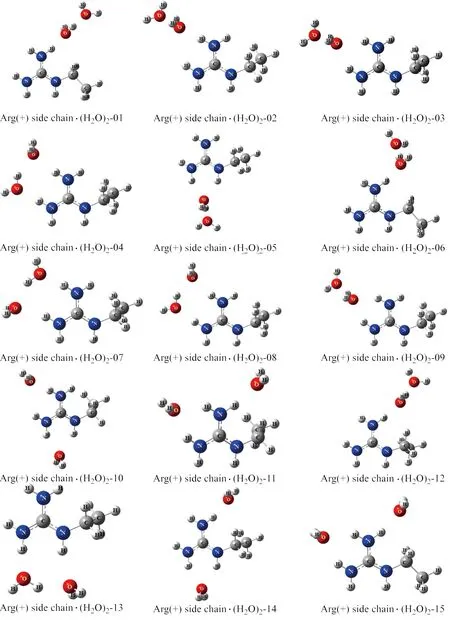
图1 15个由精氨酸侧链与水形成的三聚体复合物Fig.1 15 Trimeric complexes formed by 15 arginine side chain interacting with water molecules
V2b(i,j)=E(i,j)-E(i)-E(j),
(1)
(2)
V3b(i,j,k)=E(i,j,k)-E(i,j)-E(i,k)-E(j,k)+E(i)+E(j)+E(k),
(3)
(4)
基于课题组前期的研究基础,本文采用了静电作用函数、范德华作用函数和轨道作用函数构建了一种适用于质子化精氨酸分子的分子间相互作用势函数. 与传统的力场方法不同,这个势函数的静电相互作用部分是基于可极化的化学键偶极矩建立的,其具体函数形式如式(5)所示:
(5)
(6)
其中,δμA-B代表了分子中A-B键的诱导偶极矩,μ0,A-B是无外部作用时A-B键的固有偶极矩,qind,A和qind,B分别是采用AM1方法计算得到的复合物的A-B键上A原子和B原子的电荷,qind,A,0和qind,B,0分别是无外部作用下分子中A-B键上A原子和B原子的电荷.
在前期研究工作的基础上[5-8],本文对精氨酸侧链相关参数,尤其是胍基部分进行了参数化. 表1给出了本文确定的相关参数.

表1 本文所确定的参数Table 1 Parameters determined in this work
基于上述参数,计算了训练集中的15种构象的二体和三体作用能,如表2所示. 表中列出了采用MP2/aug-cc-pVTZ和本文方法计算得到的二体作用能和三体作用能的数值,以及本文方法与MP2/aug-cc-pVTZ的绝对误差. 该结果显示,重新拟合的参数能够准确计算这些复合物的二体和三体作用能.
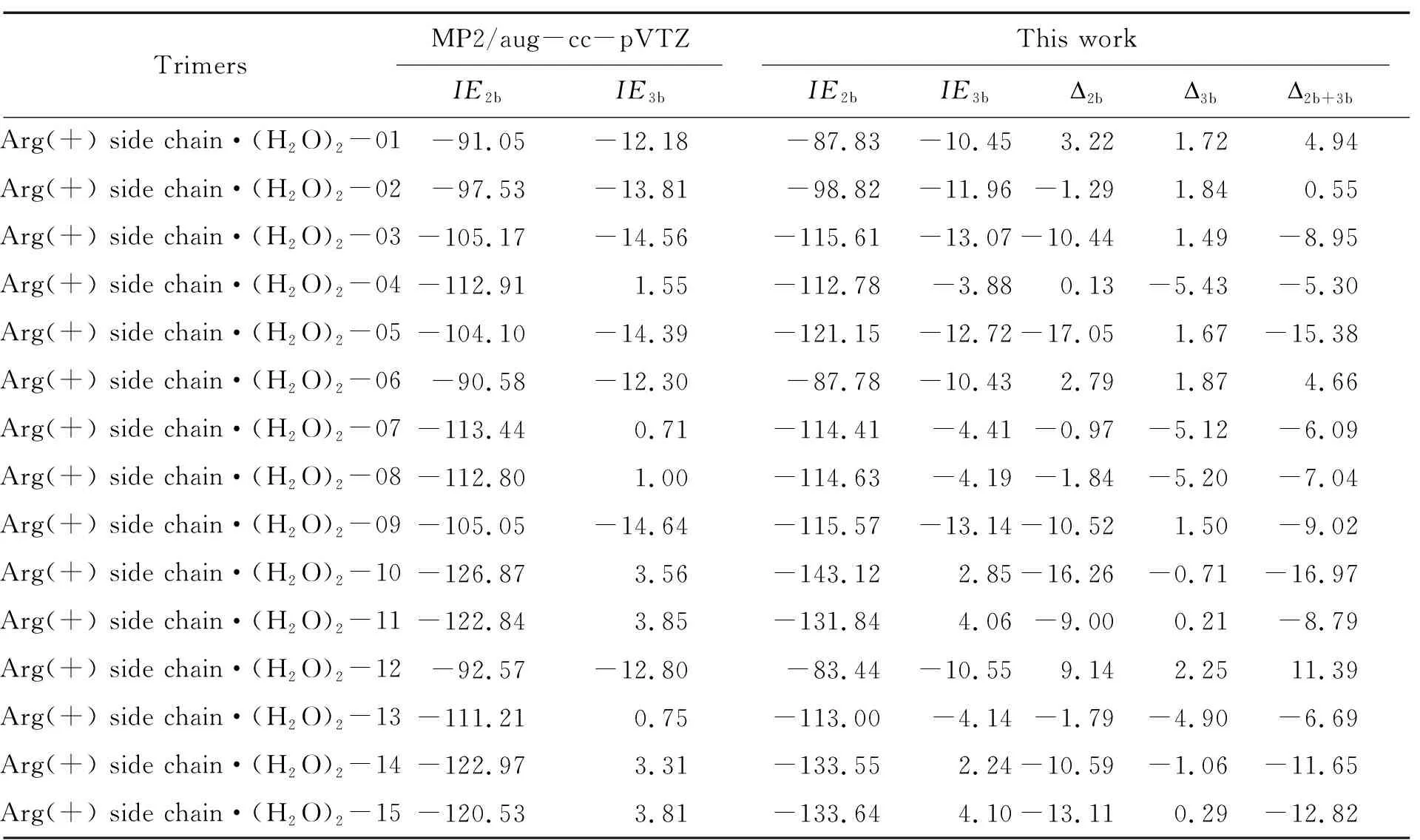
表2 采用不同方法计算15个质子化的精氨酸侧链与水分子复合物的二体作用能、三体作用能及相应绝对误差Table 2 Two-body interaction energies,three-body interaction energies,and corresponding absolute errors calculated using different methods for 15 protonated arginine side chain-water complexes kJ·mol-1
2 应用
利用前述优化后的偶极-偶极作用模型式(5)和式(6)和表1中提供的参数,对一系列含有质子化精氨酸侧链的水分子团簇[Arg(+) side chain·(H2O)n,(n= 8,10,12,15,18,20)]的二体和三体作用能进行了研究,并与高精度的MP2/aug-cc-pVTZ水平结果进行比较. 一系列含有质子化精氨酸侧链的水分子团簇的结构均取自分子动力学模拟. 分别以轨迹中精氨酸侧链分子及其周围的8、10、12、15、18和20个水分子组成的复合物为基础,在B3LYP/6-31+G(d,p)水平上进行结构优化,得到了如图2所示的6个质子化精氨酸侧链与水分子形成的稳定团簇结构.
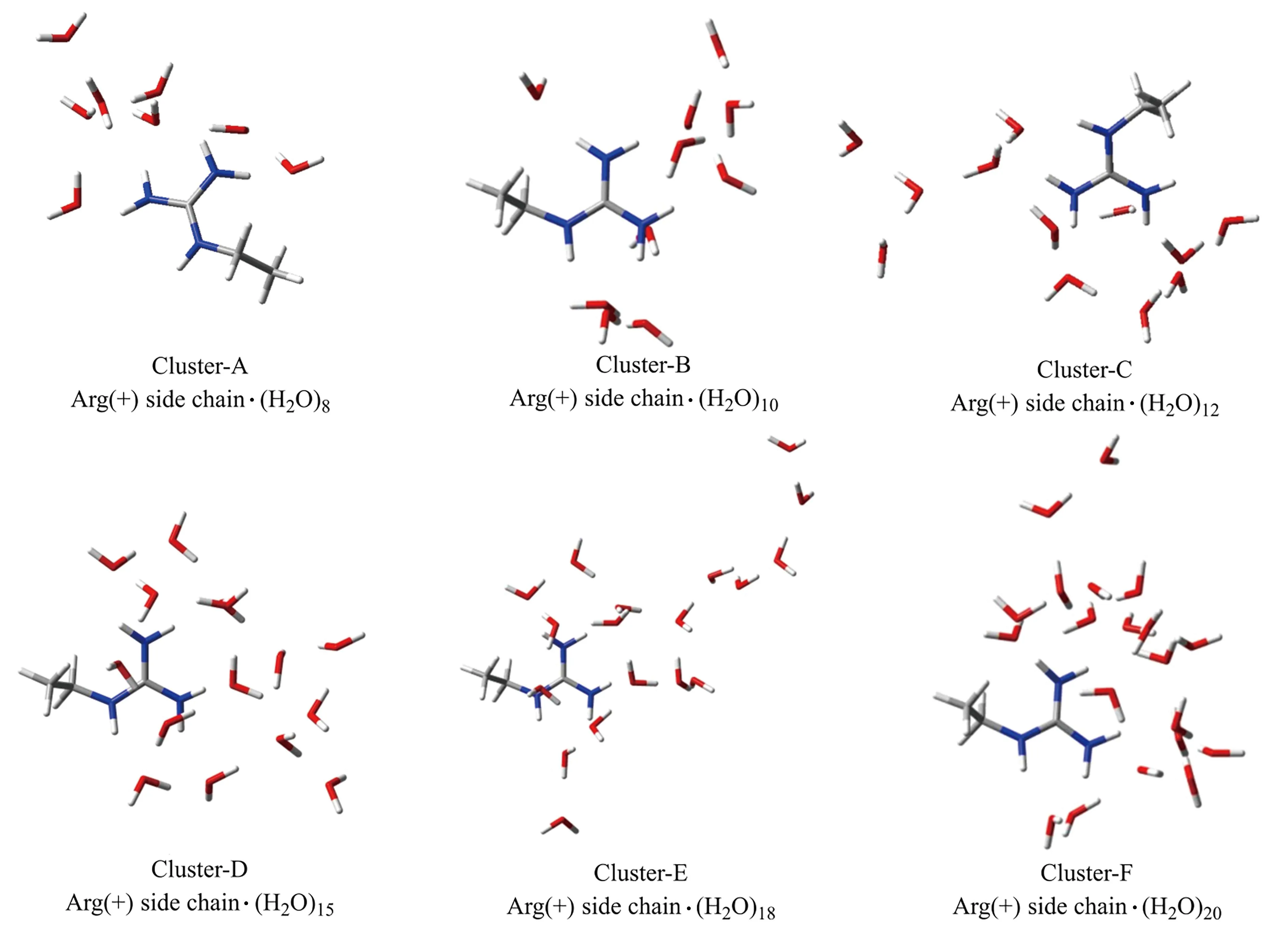
图2 质子化的精氨酸侧链分子分别与8、10、12、15、18和20个水分子形成的团簇Fig.2 Clusters formed by protonated arginine side chain with 8,10,12,15,18,and 20 water molecules
从测试团簇分子结构上讲,6种不同尺寸的水分子团簇中含有大量的分子间氢键作用. 不同于中性团簇分子,质子化的精氨酸侧链分子与水分子间的氢键作用更强,构建的稳定团簇中,N-H…O型氢键的平均键长仅为0.211 nm. 其中,最短氢键键长为0.184 nm,最长氢键键长为0.293 nm.
二体和三体相互作用在分子间相互作用研究中扮演着至关重要的角色,其重要性不言而喻. 事实上,这两种相互作用的贡献在分子之间的总相互作用中可占95%以上. 作为一种分子力场模型,它们能够以极高的准确性预测分子团簇中的二体和三体相互作用,这对于深入探讨大分子系统的性质以及理解分子间相互作用的本质至关重要.
表3列出了MP2/aug-cc-pVTZ和本文方法计算的6个质子化精氨酸侧链与水分子形成的团簇的分子间二体和三体相互作用能,以及本文方法与MP2/aug-cc-pVTZ的绝对误差. 以二体作用能的计算结果为例,以MP2/aug-cc-pVTZ方法计算结果为基准,本文方法在计算这6个团簇的二体作用能时,绝对误差的平均值为8.52 kJ·mol-1,相对误差的平均值为 -1.22%. 这显示出了本文方法在计算准确度方面的卓越表现. 具体而言,本文方法计算Cluster-B [(Arg(+) side chain· (H2O)10)]团簇的二体作用能与标准数据仅相差0.17 kJ·mol-1,而最大绝对误差出现在Cluster-D[(Arg(+) side chain· (H2O)15)]团簇,其计算的二体作用能的绝对误差为25.41 kJ·mol-1,相对误差为 -3.9%.
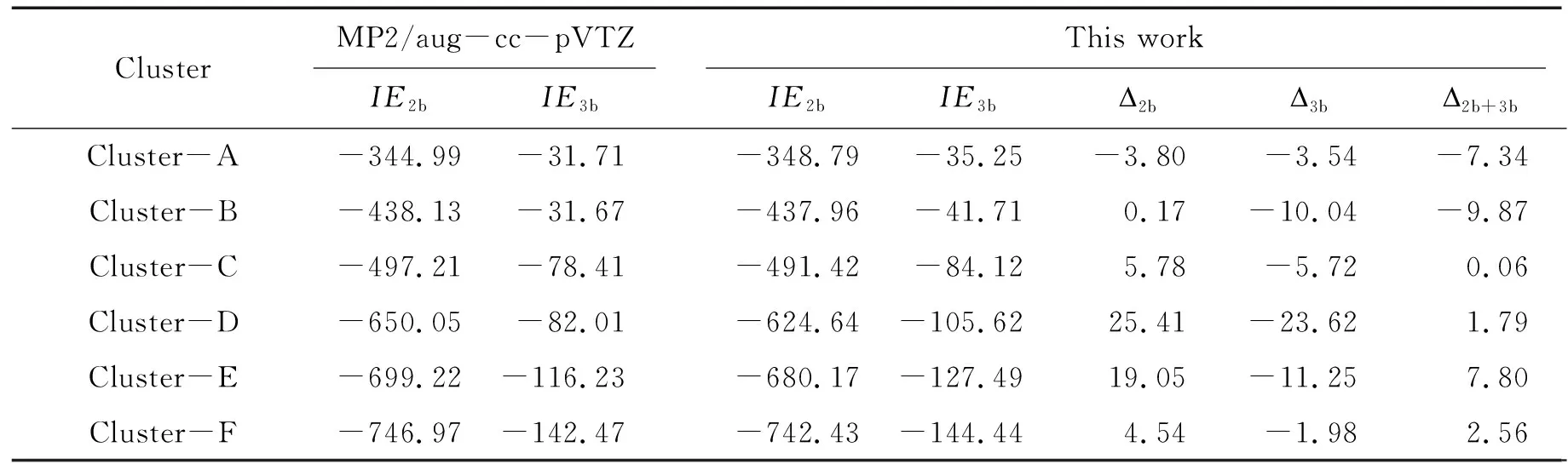
表3 采用不同方法计算质子化精氨酸侧链与水分子团簇的二体作用能、三体作用能及相应绝对误差Table 3 Two-body interaction energies,three body interaction energies,and corresponding absolute errors calculated using different methods for protonated arginine side chain and water molecules clusters kJ·mol-1
不同于仅能描述分子间二体相互作用的非极化力场模型,本文方法基于诱导化学键偶极方案将极化作用引入模型. 采用简单而有效的诱导偶极与其他偶极或电荷之间的相互作用势来描述体系的三体及以上相互作用能.在三体作用能计算方面,本文方法也显示出了较高的计算准确度,其计算结果的绝对误差的平均值为 -9.36 kJ·mol-1. 这不仅显示出了本方法能够较好地描述分子间的三体作用,同时也和二体作用能计算误差形成了有益的互补,能够更准确地描述这类团簇分子间的总相互作用.
总的来说,本文方法在预测本文所研究团簇的二体和三体相互作用能方面表现出了高准确度,绝对误差的绝对值最大为 9.87 kJ·mol-1,绝对误差的平均值为 -0.83 kJ·mol-1. 这不仅反映了本文方法在分子间相互作用能计算方面的卓越表现,同时也表明了本文方法在三体相互作用能与二体相互作用能计算的误差之间的互补性,能更准确地描述了这类团簇分子间的相互作用. 另外,值得一提的是,本文方法在不同研究系统中的计算误差没有明显地随体系规模增大而增加,这显示出了它在应用和推广方面的出色潜力.
为了更全面地评估本研究中新的诱导化学键偶极计算方法的可靠性,以及新的拟合参数在计算蛋白质分子中质子化精氨酸片段与水分子形成的团簇中的二体和三体相互作用能上的可靠性,重新构建了包含完整质子化精氨酸侧链的水团簇分子结构.具体过程如下:首先,将质子化的精氨酸分子(两端分别用氮甲基和乙酰基封端饱和)置于水盒子中,并使用NPT系综下的GTH-PBE[9]方法进行了10 ps的分子动力学模拟;其次,在平衡后的模拟中,每1 ps保存一个结构,共获得了5个质子化精氨酸分子与水分子形成的团簇. 需要强调的是,为了保证参考数据的计算准确度,仅截取距离质子化胍基C原子0.45 nm以内的水分子与质子化精氨酸残基构成团簇. 这些团簇的结构如图3所示.
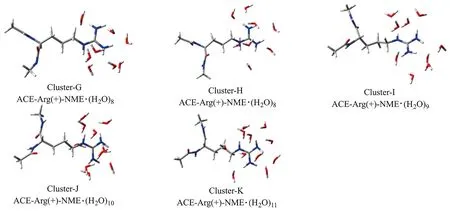
图3 质子化精氨酸二肽分子与水分子形成的团簇Fig.3 Clusters formed by protonated arginine dipeptide interacting with water molecules
分别采用RI-MP2/aug-cc-pVTZ、AMOEBAbio18[10-11]和本文方法计算上述5个团簇的总二体作用能和总三体作用能,计算结果列于表4中. 表中展示了作为基准的RI-MP2/aug-cc-pVTZ方法在计算这5个随机团簇中二体和三体作用能的结果. 同时,本文方法和常用的AMOEBAbio18可极化力场方法的计算结果也列于表中. 此外,还列出了各组数据之间的绝对误差,以便更清晰地评估这些计算方法的性能. 表中的Δ2b+3b为二体作用能和三体作用能绝对误差之和.
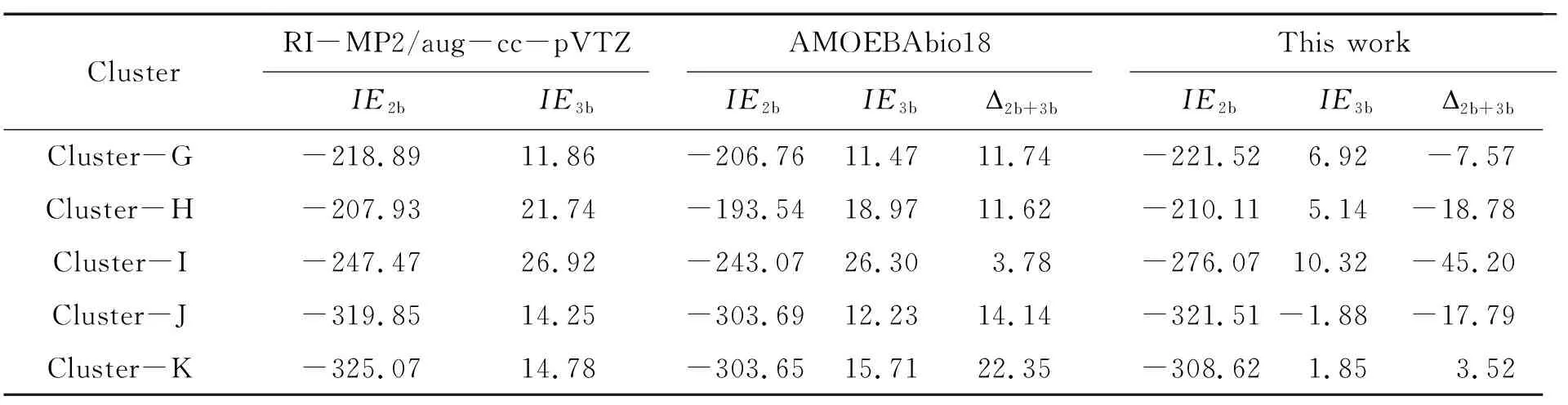
表4 采用不同方法计算封端饱和的质子化精氨酸与水分子团簇的二体作用能、三体作用能及相应绝对误差Table 4 Two-body interaction energies,three-body interaction energies and corresponding absolute errors calculated using different methods for protonated arginine dipeptide-water clusters kJ·mol-1
首先,对于Cluster-G和Cluster-H这两个拥有相同水分子数量的团簇进行讨论. 不论是使用AMOEBAbio18方法还是本文提出的方法,都能够成功预测它们的相对稳定性. 不过,值得注意的是,相较于AMOEBAbio18方法,本文方法采用了一种更为高效的非迭代化学键偶极距方案,从而实现了相当高的计算准确度. 这也反映了本文方法在计算效率上的优势. 此外,本文方法在对其他随机团簇的二体和三体相互作用能进行计算时,同样表现出了令人满意的计算准确度,这也部分证实了该计算方法和参数的可靠性.
然而,需要特别注意的是,本文中使用了原有的基于中性氨基酸的主链参数来完成质子化精氨酸主链相关作用的计算. 这导致了在含有质子化精氨酸片段的水团簇的多体相互作用能计算中,相对于含有质子化精氨酸侧链的水团簇,计算误差较大. 为解决这一问题,我们计划在未来的研究工作中进一步有针对性的优化精氨酸主链相关基团的参数,以期获得更高的计算准确度. 这个优化过程将有助于更准确地描述蛋白质中精氨酸残基与水分子的相互作用,从而提高模拟结果的可靠性.
总的来说,通过这些结果,不仅证实了本文方法在多体相互作用计算中的有效性,还展示了其在计算效率上的优势. 然而,在应对其他氨基酸残基的挑战时,还将继续努力,以进一步完善和改进本方法的计算准确度,使其更符合实际情况. 这将为分子模拟和计算化学领域提供更为可靠的工具和方法,有望在药物设计和生物化学研究中产生广泛的应用前景.
3 结 论
本研究通过引入一种新的诱导化学键偶极计算方法,成功应用于蛋白质分子中质子化精氨酸片段与水分子形成的团簇的相互作用能计算.结果表明,新方法在预测本文涉及的尺寸较大的含有质子化精氨酸侧链、二肽的随机水分子团簇的二体、三体总作用能的绝对误差的平均值为 -8.3 kJ·mol-1,相对误差的平均值为3.8%,表现出了良好的计算准确度.在计算量上还明显小于常用的可极化力场方法.然而,在处理精氨酸主链相关作用时,也面临一些挑战,需要进一步改进相关参数以提高计算准确度. 这一研究为理解分子间相互作用,尤其是带电荷片段间的相互作用提供了重要的工具和方法,对于药物设计、生物物理化学等领域的研究具有积极的影响,为未来的科学研究提供有益的参考.

