HQEFT框架内半轻衰变的相关研究
左亚兵, 田婧赢, 金洪瑶, 朱嘉利, 凌 汶
(辽宁师范大学 物理与电子技术学院,辽宁 大连 116029)
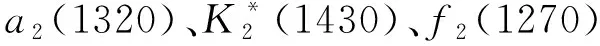
1 强子矩阵元的形状因子描述与光锥求和规则推导
1.1 强子矩阵元的形状因子描述
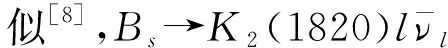
(1)
(2)

在HQEFT框架内,对式(1)、式(2)等号左边的强子矩阵元做重夸克展开,只考虑领头阶贡献[11-12],有
(3)

(4)
其中,
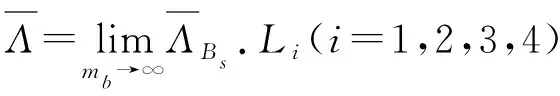
(5)
(6)
(7)
(8)

1.2 光锥求和规则推导
下面利用光锥求和规则计算领头阶波函数Li(i=1,2,3,4).与末态为2++轻张量介子情形类似[8],首先定义如下真空-K2介子关联函数:
(9)
(10)
其中,T表示算符的编时乘积.
从唯象学角度,在式(9)、式(10)不同时空点流算符中插入具有Bs介子量子数的态的完备集,得到
(11)
(12)
将式(3)、式(4)代入式(11)、式(12),有
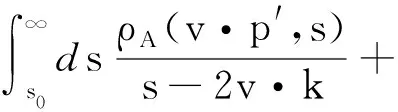
(13)
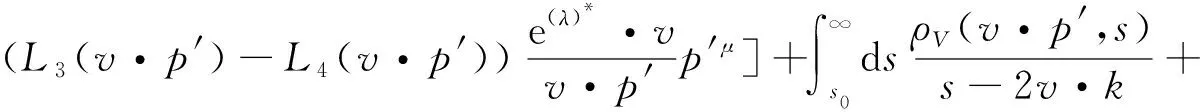
(14)
其中,F为HQEFT中的有效重介子衰变常数[13].k=(p′+q)-mbv,表示Bs介子的残余动量.积分项表示来自高共振态的贡献.减除项的引入是为了保证积分收敛,做Borel变换后自动消失,不影响物理结果.
另外,也可以从理论角度对关联函数式(9)、式(10)进行计算,写为
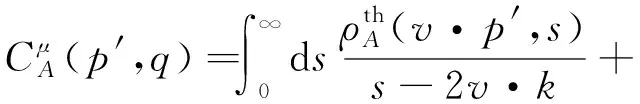
(15)
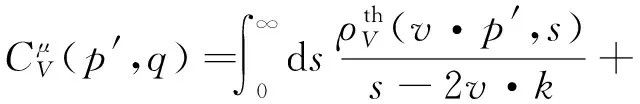
(16)
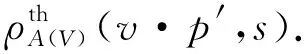
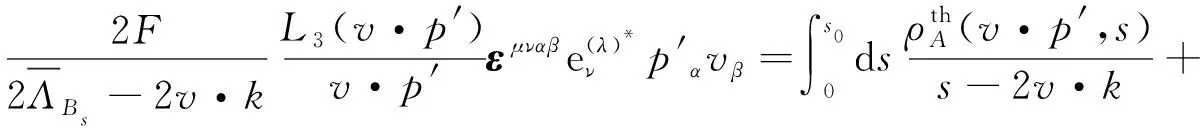
(17)
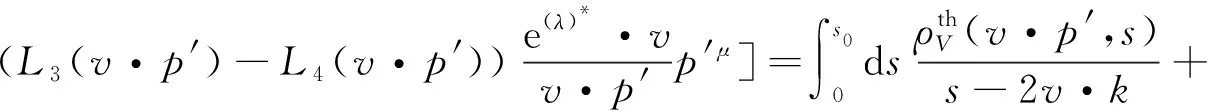
(18)
定义y=v·p′,ω=2v·k,对式(15)、式(16)连续做两次Borel变换,有
(19)
(20)
在HQEFT框架内,重夸克展开至领头阶计算关联函数式(9)、式(10)并代入式(19)、式(20),可以得到
(21)
(22)
这里,{φ‖(u),φ⊥(u)},{gv(u),ga(u),ht(u),hp(u)},{g3(u),h3(u)}为末态K2(1820)介子的光锥分布振幅,扭度分别为2、3、4.这些分布振幅定义如下[10]:
(23)
(24)
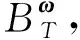
(25)
(26)
(27)
(28)
2 数值结果与分析
2.1 形状因子
利用式(5)~式(8)和式(25)~式(28)式计算Bs→K2(1820)跃迁形状因子涉及末态K2(1820)介子的光锥分布振幅.这里,考虑分布振幅到扭度3,采用文献[10]通过QCD求和规则给出的结果.
(29)
(30)
(31)
(32)
(33)
(34)
其中,
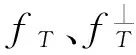
其他相关输入参数的取值如下[1,11-13],
mBs=5.37 GeV,mq=0.002 GeV,ms=0.093 GeV,mT=1.82 GeV,
式(25)~式(28)中的s0和T为自由参数,前者与初态Bs介子的阈值能量相关,后者为Borel变换参数.根据LCSR的要求,选取跃迁形状因子随这2个自由参数变化最稳定的区域作为其取值范围.Bs→K2(1820)形状因子在q2=0时的值随Borel变换参数T的变化曲线如图1所示.不同形式的曲线(实线、虚线、点划线)对应不同的s0取值.从图1可以看出,自由参数s0、T可以在如下范围内取值:
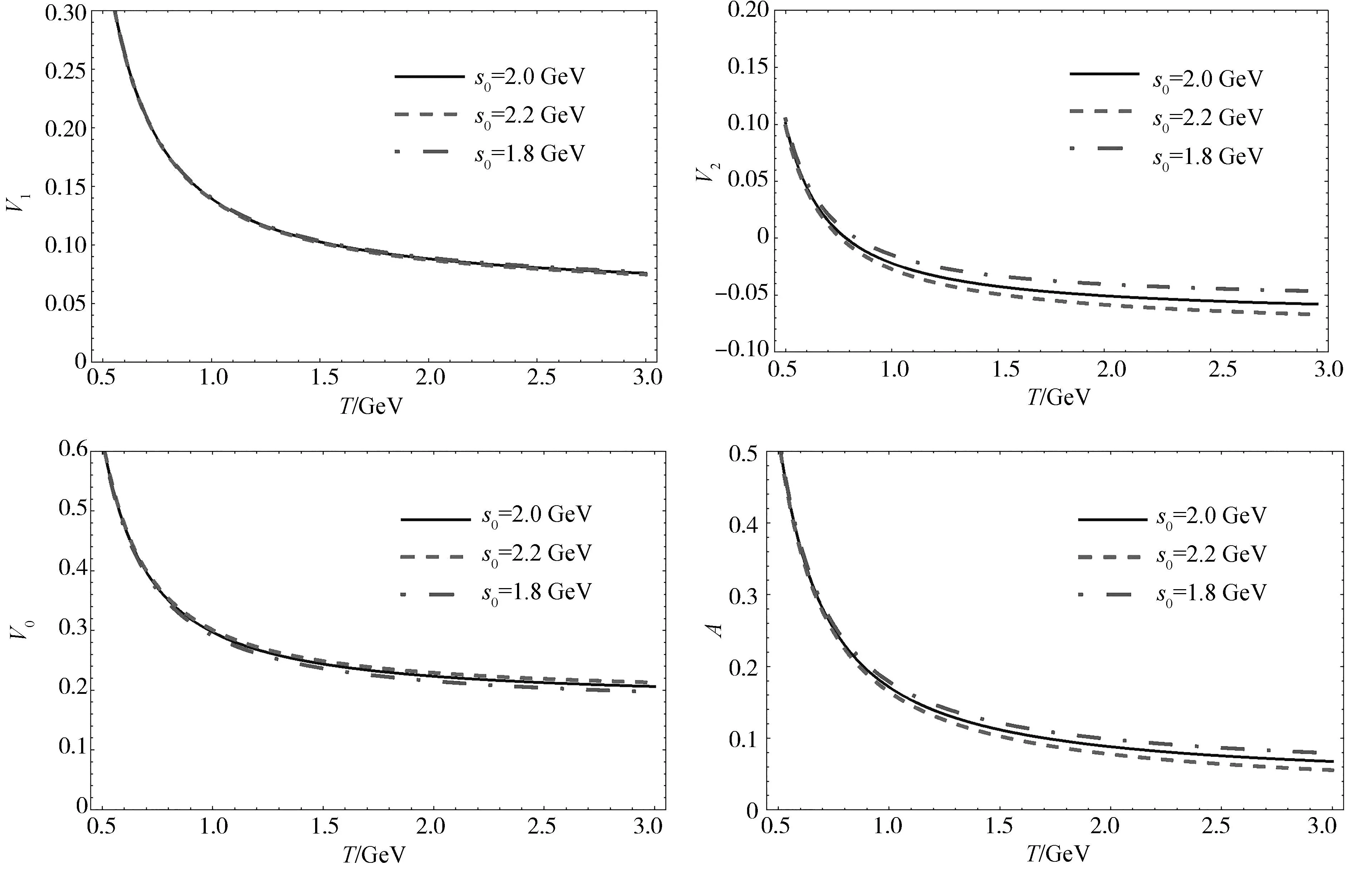
图1 Bs→K2(1820)形状因子在q2=0时的值随T的变化曲线Fig.1 Bs→K2(1820) form factors as functions of T at q2=0
s0=2.0±0.1 GeV,T=2.0±0.3 GeV.
由于LCSR在大q2区域不再可靠,采用如下参数化方式将LCSR在小q2区域给出的结果延拓到整个物理区域:
(35)
其中,F∈{V1,V2,V0,A}.图2给出了延拓后得到的Bs→K2(1820)跃迁形状因子在整个物理区域内随q2的变化曲线.可以看出,形状因子V1、V0随着q2的增大而增大,V2随着q2的增大而减小,A几乎不随q2变化.跃迁形状因子的数值结果在表1中给出.与相应2++张量介子情形不同,跃迁形状因子V2<0.形状因子的误差来自自由参数s0、T的取值,在5%~20%范围内.

表1 Bs→K2(1820)形状因子的数值结果.其中,拟合参数aF、bF的第一、第二和第三个值分别对应形状因子的中心值、最大值和最小值Table 1 Numerical results of the Bs→K2(1820) form factors,where the first,second and third values of fitting parameters aF,bFcorrespond to the central,maximum and minimum values of form factors,respectively

图2 Bs→K2(1820)形状因子在整个物理区域内随q2的变化曲线Fig.2 Bs→K2(1820) form factors as functions of q2in the whole physical region
(36)
其中,
(37)
(38)
(39)
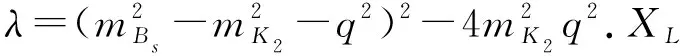

(40)
纵向极化分数:
(41)
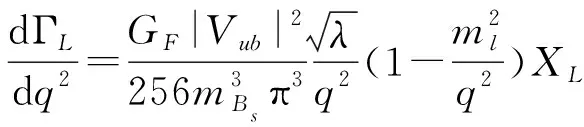
微分前后不对称:

(42)
总的前后不对称:
(43)
对于Bs介子寿命τBs、带电轻子质量ml、CKM矩阵元|Vub|、费米耦合常数GF和约化普朗克常数ħ,采用粒子数据组(PDG)给出的最新结果[1]:
τBs=1.52×10-12s,me=0.51×10-3GeV,mμ=0.106 GeV,mτ=1.777 GeV,
|Vub|=(3.82±0.20)×10-3,GF=1.166×10-5GeV-2,ħ=6.582×10-25GeV·s.

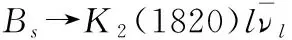
表2 半轻衰变Br、fL、AFB、c0的数值结果Table 2 Numerical results of Br,fL,AFB,c0for the semileptonic decays
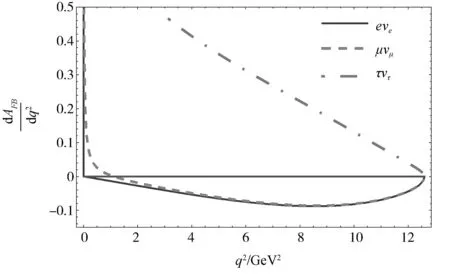
图3 半轻衰变微分前后不对称随q2的变化曲线Fig.3 The differential forward-backward asymmetries as functions of q2for the
3 结 论
在HEQEFT框架内,利用LCSR的方法对Bs到D波2--张量介子K2(1820)半轻衰变进行了研究.首先,考虑K2(1820)光锥分布振幅到扭度3,重夸克展开至领头阶,利用LCSR计算了相关的跃迁形状因子Vi(i=0,1,2)、A.计算表明,与相应2++张量介子情形不同,形状因子V2在所取自由参数(s0、T)范围内小于0.跃迁形状因子的误差来自s0、T的取值,在5%~20%区间内.

