基于奖励与策略双优化的机械臂控制算法

申 珅,曾建潮,,秦品乐

(1.中北大学 电气与控制工程学院,山西 太原 030051; 2.中北大学 计算机科学与技术学院,山西 太原 030051)

0 引 言

随着工业装备的快速发展,机械臂在生产领域的应用不断增加,各类提升机械臂性能的智能控制算法层出不穷。机械臂端到端的控制方法主要分为强化学习、模仿学习和迁移学习这三种方法[1]。其中,与环境直接交互的强化学习算法在机械臂控制领域的应用尤为广泛[2],然而,强化学习在高效训练高自由度的工业机械臂的应用中仍然存在一些问题,即由无效动作导致的训练周期过长、收敛速度慢的问题。

为了解决强化学习训练高自由度的工业机械臂效果不佳的问题,国内外学者普遍采用两类方法来进行优化。

第一类方法是通过对强化学习算法的泛用性进一步优化,以实现减少无效动作的目的。Schulman等[3]令策略网络服从一个分布,提出信赖域策略优化(Trust Region Policy Optimization,TRPO),实现了机械臂在连续动作空间的策略优化; Kalashnikov等[4]提出QT-Opt算法,令7台机械臂收集58万次抓取数据,用来训练神经网络以作为机械臂控制器; Yahya等[5]提出自适应分布式指导策略搜索(Adaptive Distributed Guided Policy Search,ADGPS),让多个机械臂分别训练并进行经验分享,减少试错数并寻找最优路径; Haarnoja等[6]结合Q函数与交叉熵,提出软Q学习算法(Soft Q-Learning,SQL),大大提高了机械臂控制的鲁棒性,并结合AC算法,提出软演员-评论家算法[7](Soft Actor-Critic,SAC),缩短了算法训练的时间; Zhang等[8]设计了一种改进SAC算法来应用于机械手的操控; Zhong等[9]结合DDPG算法与逆运动学,提出一种时变的混合机械臂控制算法; Iriondo等[10]基于双延迟深度确定性策略梯度算法(Twin Delayed Deep Deterministic Policy Gradient,TD3)研究了移动机械手在桌子上拾取物体的操作; Ranaweera等[11]通过域随机化和在强化学习训练过程中引入噪声,提高了训练效果; 苏杰等[12]改进DDPG应用于机械臂轨迹运动。这一类方法的核心思想是通过引入概率论的方法,大幅度减少无效动作带来的影响,但是该类方法并不能根除无效动作。

第二类方法是将强化学习与模仿学习相结合,由先验数据对强化学习进行约束,以实现稳定运行的目的。Finn等提出的GCL算法是在MaxEntIRL的基础上对机械臂进行轨迹约束,并将人为示教轨迹直接作为最优方案来引导强化学习进行训练[13-14]; Ho等[15]在GCL基础上,提出了生成对抗模仿学习算法(Generative Adversarial Imitation Learning,GAIL),筛选出与示教轨迹相似度高的采样轨迹,降低了无效动作出现的可能,提高了训练速度; Eysenbach等[16]提出逆向强化学习,根据示教数据导出通用的奖励函数; Yu等[17]提出并验证了一种基于改进IRL的机器人手眼合作模型,使机器人获得了高效的决策性能; Sun等[18]结合DQN和行为克隆,提出了一种新的DRL算法 (D3QN),显著降低了训练初期探索的盲目性; Peng等[19]提出了Deep Mimic算法,将奖励函数来拆分成数个模仿分量的指数和,利用复合奖励函数来训练强化学习; Escontrela等[20]提出了AMP算法,将复合奖励函数拆成模仿分量和目标分量,提高了生成动作的有效性。卢彬鹏[21]通过图像处理技术来获取训练强化学习所需的示教数据; 傅海涛[22]通过加设传感器来进行外设示教。这一类方法的优点是利用轨迹优化中存在的可行解来作为强化学习的约束,但是其泛化性相较于第一类方法较差。

综上所述,本文针对两种方法各自存在的缺陷,提出了一种新的算法,即先通过第二类方法来训练,再引入第一类方法来提高机械臂控制器的鲁棒性,具体研究内容如下:

1) 提出一种基于模仿分量与任务分量构建复合奖励函数的方法,在强化学习的训练阶段提高控制器的鲁棒性。

2) 提出一种基于奖励与策略双优化的机械臂控制算法HR-GAIL,构建奖励与策略的二元变量损失函数,在奖励与策略交替优化的过程中实现对控制器的更新。

3) 在Pybullet仿真环境中批量生成示教数据,并进行仿真训练和实验,与GAIL+SAC方法进行对比来验证本文方法的有效性。

1 机械臂控制基本原理

1.1 机械臂控制框架

机械臂控制系统由传感器、控制器、执行器和被控对象组成,各部分之间的关系如图1 所示。环境的内置传感器识别当前的状态s,该状态信息随后被输入到控制器中。强化学习算法的策略网络作为机械臂的控制器,通过输出动作指令a改变机械臂关节电机和手爪电机的力矩值,从而实现对被控对象的控制。机械臂与被控对象的交互导致环境的改变,传感器识别新状态s′后继续输入到控制器中进行下一步控制。

1.2 机械臂控制器的设计

机械臂控制器的设计参考SAC的框架,仅提取SAC的策略网络作为控制器。策略网络由层数为n的多层全连接神经网络构成,输入状态s后,在神经网络的输出端可以得到对应动作的均值μ与标准差σ,由此来构建多元正态分布模型。通过对该多元正态分布进行采样,在机械臂控制器的输出端得到采样动作a与该采样动作的概率值p。机械臂控制器的设计如图2 所示。

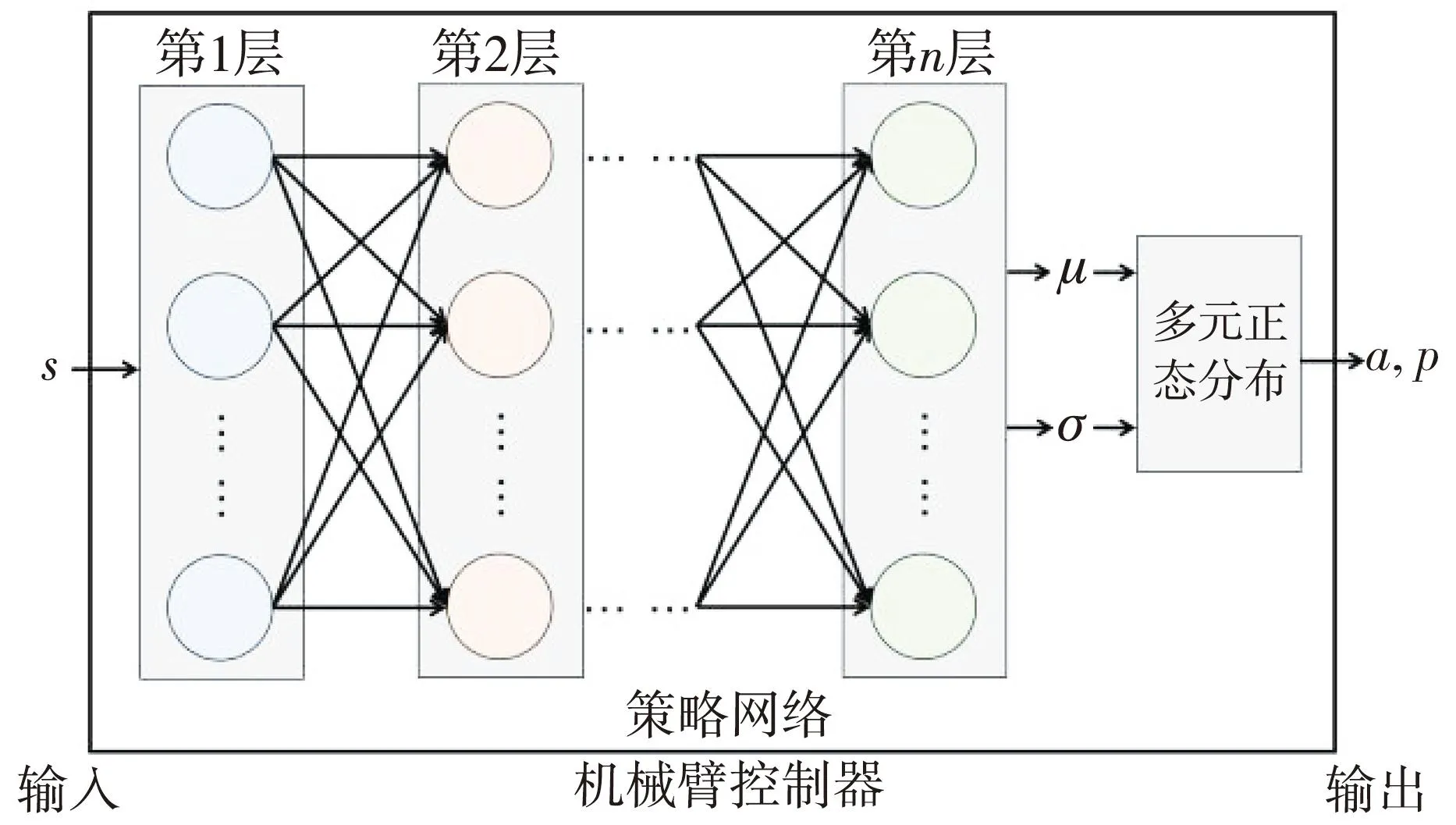
图2 机械臂控制器的设计

控制系统的执行机构是Franka Emika Panda机械臂,该机械臂有7个关节电机,末端执行器上安装了2指手爪,其结构以及各关节的坐标系位置如图3 所示。

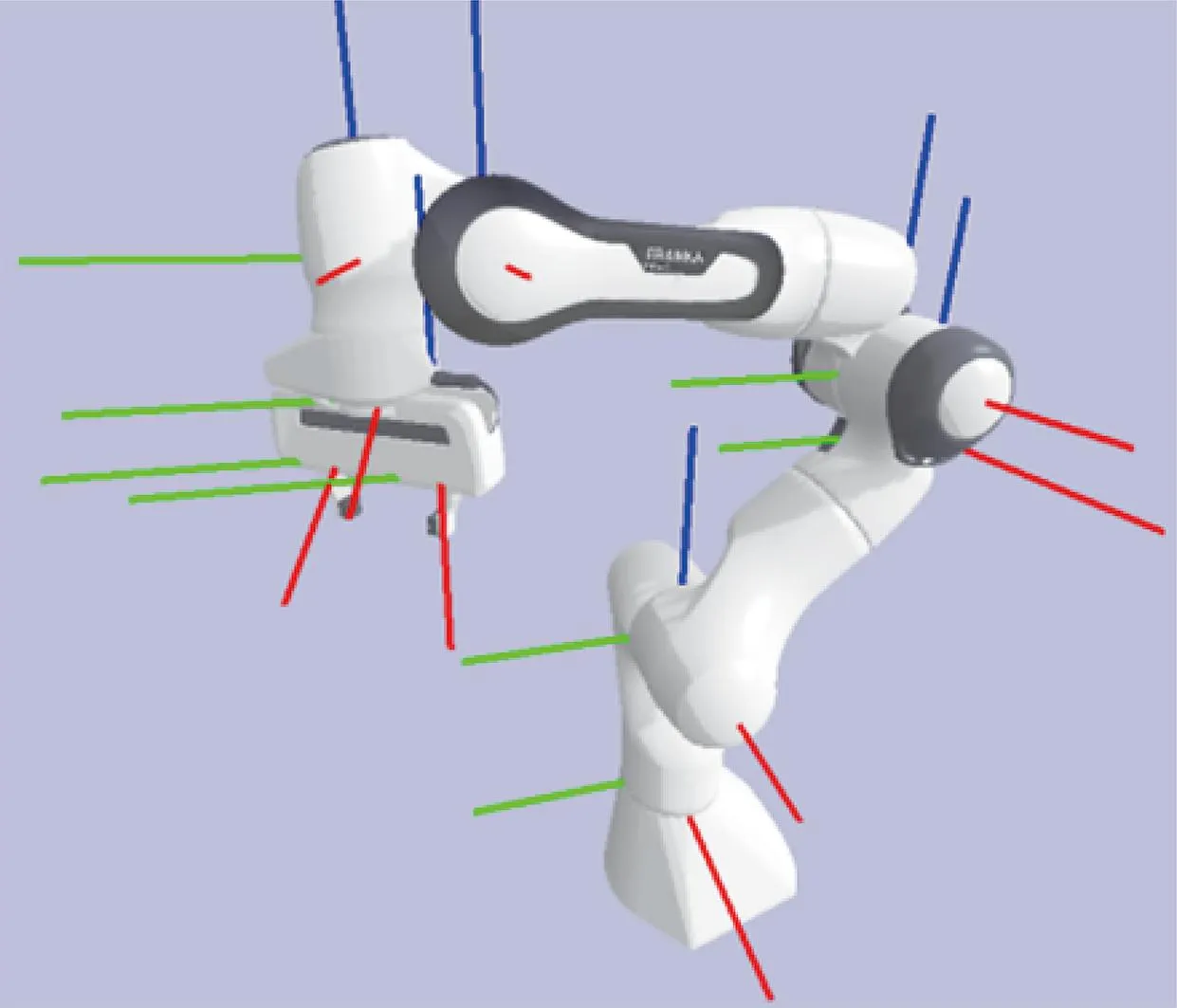
图3 Franka Emika Panda机械臂

每一时刻t下的状态st由7个关节角以及手爪2指上的平移位置构成,表示为

st=[θ1,θ2,θ3,θ4,θ5,θ6,θ7,d1,d2]T。

(1)

每一时刻t下的动作at由7个关节角速度以及手爪2指所施加的力构成,表示为

(2)

式中:M为手爪电机的力矩值。当手爪对目标物块施加一定的压力后,才能通过摩擦力提起物块。因此,需要通过输出手爪电机的力矩值来驱使手爪进行相应的抓取动作。

动作概率pt是策略网络πθ在状态st所采样动作at的动作概率,表示为

pt=πθ(at|st)。

(3)

2 基于奖励与策略双优化的改进算法

2.1 复合奖励函数的构成

奖励函数是评价强化学习效果的重要指标。本节算法参考DeepMimic算法构建复合奖励函数,即每个奖励函数的分量都是由当前分量与示教数据的差的2范数构成。求取该差值的自然指数后,再将各奖励函数的分量进行加权求和。

(4)

式中:Pe是机械臂末端手爪的位姿;Pc是目标物块的位姿;Pt是目标位置的位姿;α,β是权重系数,这里分别设定为6和12。

log[sigmoid(fη(st,at)-logπ(at|st))],

(5)

式中:Dπ是鉴别器; sigmoid(x)的表达式为[1+exp(-x)]-1;π(at|st)是动作概率;fη是鉴别器网络,其网络结构如图4 所示。

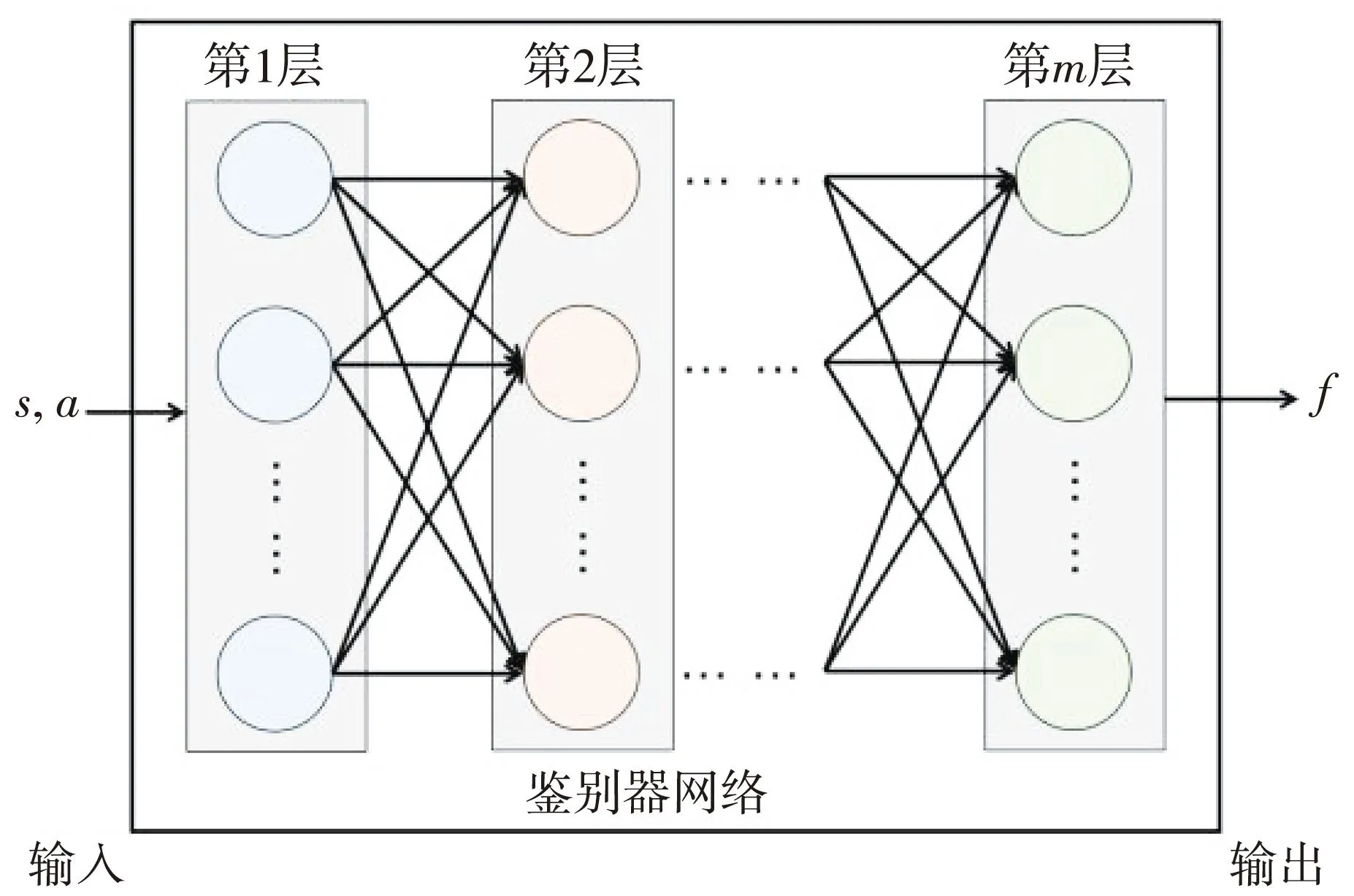
图4 鉴别器网络结构

输入状态s和动作a的信息后,在层数m的多层全连接神经网络的输出端得到鉴别器f的值。

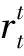
(6)

式中:Q是复合奖励函数,表示从当前时刻t到末端时刻T的累计奖励; 参数γ是模仿分量的权重,这里设定为0.7。

2.2 改进算法框架

本文在复合奖励(Hybird Reward)的基础上改善GAIL,并在SAC的策略网络进行优化,该方法命名为HR-GAIL。HR-GAIL先确保示教样本和采样样本之间的分歧最小化,进而优化奖励函数和策略网络。奖励函数和策略网络的复合映射为

H(π)+Eπr(s,a)-EπEr(s,a)],

(7)

式中:π为控制器的执行策略;πE为示教演示的执行策略;H(π)为熵;r(s,a)为奖励函数;Eπr(s,a)为在π分布上对奖励r所求的期望;EπEr(s,a)为在πE分布上的期望;ψ为归一化函数,其表达式[15]为

ψ(r)=EπE{-r+φ[-φ-1(-r)]},

φ=-logD。

(8)

HR-GAIL分别构建基于策略网络πθ的采样鉴别器Dπθ和基于示教轨迹的示教鉴别器DπE,其表达式分别为

Dπθ(st,at)=sigmoid(fη(st,at)-

logπθ(at|st)),

DπE(st,at)=sigmoid(-fη(st,at))。

(9)

HR-GAIL在鉴别器网络fη上叠加偏置项logπθ(at|st),目的是增加鉴别器网络fη的鲁棒性,再经过函数sigmoid函数处理,得到采样鉴别器Dπθ的值。将该方法同样应用在示教鉴别器DπE,示教动作概率πE(at|st)是确定的,故其值取1,则logπE(at|st)的值取0。

联立式(6)～式(9),则二元变量的损失函数为

L(πθ,fη)=-λH(πθ)+EπθQ+EπElogDπE,

(10)

式中:λ∈(0,1),是熵的正则项,这里设定为0.2。在二元变量损失函数的基础上,分别对参数η和参数θ求偏导数,可得

在高校经济管理教学过程里，在校企合作模式的前提下充分掌握企业所需要人才方向，根据依据定制出符合企业所需人才培养方案，校企合作模式下校企双方通过相应方式在企业建设实习基地，企业定期提供实习场所、实习机会，高校定期将优秀毕业生安排到企业工作，这种模式将学校与企业紧密结合，学生的实习成果可以帮助解决企业一些实际问题，在创造企业效益的前提下，学校降低了教育成本。学生通过实习能够更熟练的运用所学知识，也解决了学生自身就业问题。经济学管理教学中运用校企合作模式能够更好的了解企业所需人才类型，进一步根据企业需求制定有针对性的专业人才。

ηL(πθ,fη)=Eπθ[γηlogDπθ(s,a)]+

EπE[ηlogDπE(s,a)],

(11)

θL(πθ,fη)=-λθH(πθ)+

Eπθ[γ∇θlogDπθ(s,a)]。

(12)

改进算法框架如图5 所示。

图5 改进算法框架

控制器是参数为θ的策略网络,根据状态s,输出动作a与动作概率p。动作a作用在机械臂上并在环境交互,得到新状态s,然后再进行下一步循环。每一次交互都会把s,a,p保存在数据缓存器的采样轨迹分区。

2.3 机械臂控制器的训练

首先计算机械臂末端手爪位姿与物块位姿的位置差和角度差,并引入反运动学公式,输出下一个状态下机械臂的各关节所对应的角度值; 然后手爪锁定物块,计算出机械臂末端手爪位姿与目标位置的位置差和角度差,并引入反运动学公式,使手爪带动物块移送到目标位置; 最后运用筛选机制,从上千条运动轨迹中选出符合用户需求的示教数据簇。生成示教数据的流程如图6 所示。

在控制器的训练阶段,从数据缓存器中采样批量数据,根据式(10)的损失函数,计算关于θ的梯度,实现对策略网络πθ的参数更新。综上所述,机械臂控制器训练过程的伪代码如算法 1 所示。

算法1：机械臂控制器训练过程

输入:最大迭代次数tmax,数据缓存器B,鉴别器网络fη

输出:训练好的策略网络πθ

程序开始

1.从B中分别对示教轨迹和采样轨迹采样

2.for 每一次迭代

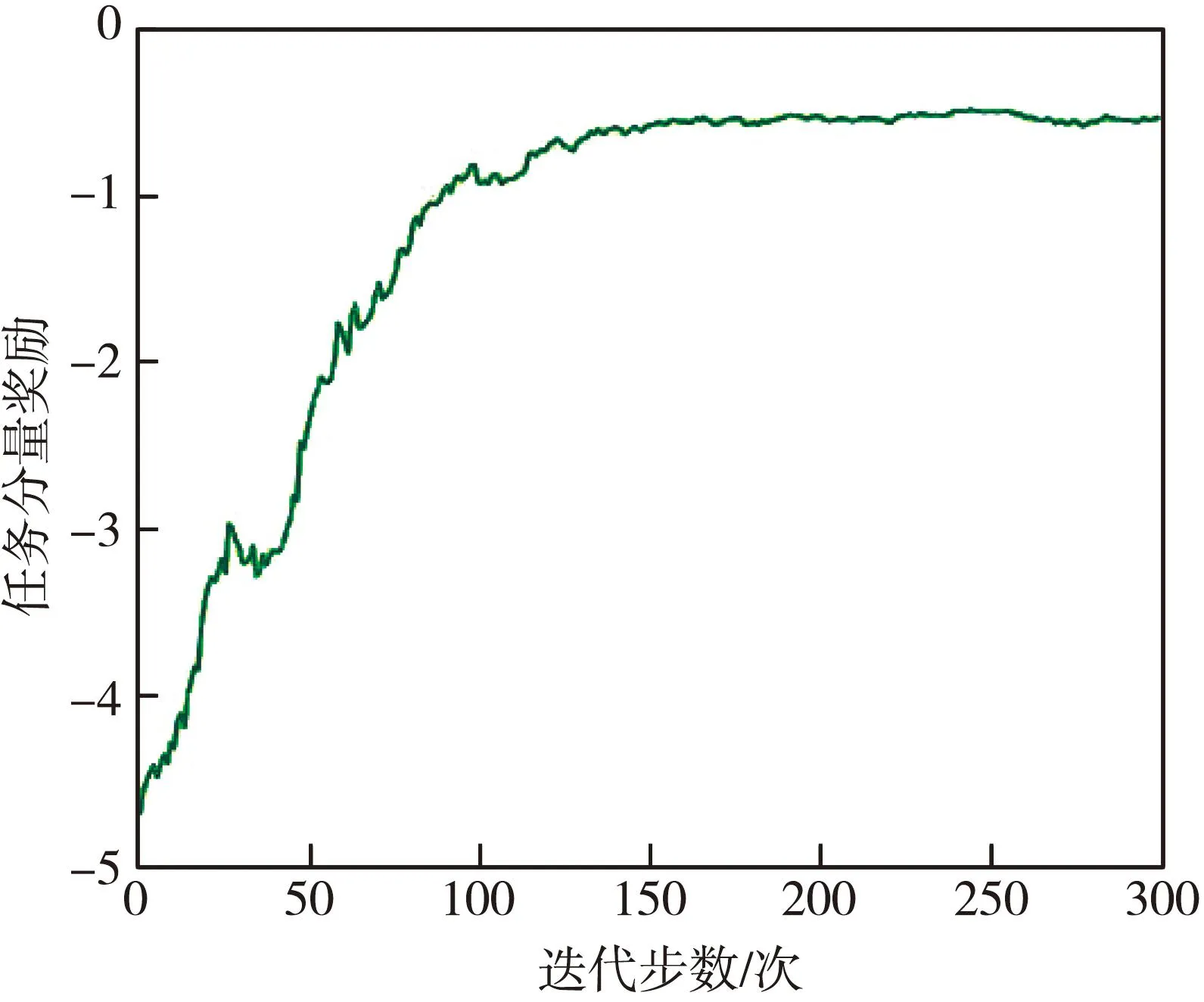
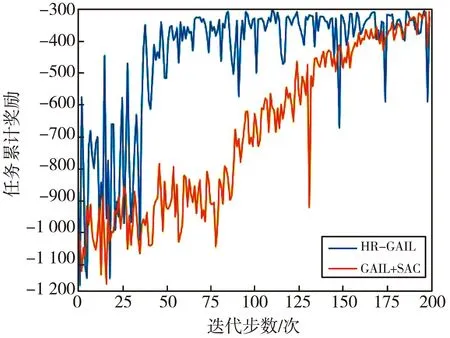
3.whilet

4. 获取状态st

5. 由控制器πθ采样at,pt

6. 计算Dπθ(st,at)和DπE(st,at)

7. 仿真出st+1

9. end while

10.根据式(11),计算奖励梯度更新fη

11.根据式(12),计算策略梯度更新πθ

12.end for

程序结束

3 实 验

3.1 仿真环境配置

本系统所使用的硬件设备为LAPTOP-4KUQUNRQ,内置的GPU芯片的型号为GeForce RTX 2080 Ti,处理器为Intel(R) Core(TM) i5-6200U CPU @ 2.30 GHz,内存为16 GB。使用的仿真软件为Python3.6,物理仿真驱动为Pybullet3.1.7,调用基于Pytorch1.5.1+cpu和Pytorch1.5.1+cuda框架的神经网络算法。

基于Pybullet引擎构建的机械臂模型仿真系统,并应用在抓取及移动物块的场景中,如图7 所示。机械臂模型仿真系统包括Franka Emika Panda机械臂URDF模型、分拣台、目标物块、目标位置和控制滑块。

图7 机械臂模型仿真系统

根据D-H模型方法[23],由沿xi-1坐标轴的有向距离ai,沿zi-1坐标轴的有向距离di,x坐标轴间夹角αi,z坐标轴间夹角θi来构建机械臂的几何模型,同时,θi是实时获取的状态信息。Panda机械臂D-H参数如表1 所示。

表1 Panda机械臂D-H参数

计算坐标系两两之间的变换矩阵,得到机械臂基座到机械臂手爪的总变换矩阵,由此计算出逆运动学公式,并按照图6 的流程生成示教数据,并最终采集2 000条示教轨迹记录在数据缓存器中。该示教轨迹将在神经网络的训练环节中重复使用,后续经由HR-GAIL算法产生的轨迹将作为采样轨迹,同样记录在数据缓存器中。

HR-GAIL算法中神经网络的参数设置如表2 所示。

表2 HR-GAIL算法中神经网络的参数设置

3.2 抓取效果仿真

机械臂控制器搭载HR-GAIL算法进行训练,当各神经网络参数稳定后,改变目标物块位置,进行抓取效果仿真,如图8 所示。

图8 抓取仿真效果图

仿真结果表明,机械臂手爪能精准抓取物块,并稳定地移动到目标位置。

3.3 对比实验

根据数据缓存器里的数据,分别计算300次迭代训练下的GAIL与HR-GAIL的鉴别器损失值,以验证本文奖励优化的性能。二者的鉴别器损失值如图9 所示。

(a) HR-GAIL示教鉴别器与采样鉴别器损失值

从图9(a)和图9(b)都可看出:示教鉴别器损失值都在不断减少,而HR-GAIL的示教鉴别器损失值震荡幅度小,收敛速度更快; 采样鉴别器损失值先增大后保持稳定,而HR-GAIL的采样鉴别器损失值比GAIL更快地达到稳定状态。

复合奖励函数的任务分量反映了控制器完成仿真任务的优劣情况,其随迭代步数变化的情况如图10 所示。任务分量由多个差值的2范数构成,所以最终时刻的奖励值尽可能接近0,如图10 所示,且在150步左右收敛至最大值-0.5。同时,随着迭代步数的增加,奖励值不断增大,最佳的任务累计奖励约为-300。

图10 任务分量奖励随迭代步数变化图

GAIL负责学到奖励函数的步骤,SAC在定义好奖励函数后才进行强化学习。因此,验证本文策略优化的效果,需要对比HR-GAI与GAIL+SAC在同一示教数据下,生成各自的奖励函数,再执行强化学习训练后,完成同一任务的累计奖励。二者的任务累计奖励随迭代次数变化的对比图如图11 所示。

图11 HR-GAIL与GAIL+SAC任务累计奖励对比图

由图11 可以看出,HR-GAIL在50步左右就达到了最优状态,即任务累计奖励为-300,而原方法在160步左右才达到最优,体现了本算法在高效训练机械臂方面的优越性。

令机械臂执行抓取并移动物块的任务,设置5组实验,每组实验限时6 h,对比不同方法的抓取成功率、碰撞情况和完成时间,结果如表3 所示。

表3 不同方法的仿真效果

由表3 可知,采用HR-GAIL方法的完成时间比GAIL+SAC方法缩短16%,抓取成功率提高5%。碰撞方面,其他方法没有从示教数据中学到经验,无法有效指导高自由度机械臂的动作决策,在实验过程中一直发生碰撞。

4 结 论

本文以GAIL、DeepMimic和SAC为模板进行推论,构建了基于奖励与策略双优化的机械臂控制算法HR-GAIL,用于解决强化学习在训练机械臂过程中周期长的问题。该方法变换鉴别器形式,并融合复合奖励函数,在策略网络πθ和鉴别器网络fη交替优化的过程中实现对机械臂控制器的更新优化。相比GAIL+SAC方法,本文算法在50步左右就达到了最优状态。复合奖励函数的构建能够更好地训练策略网络,使得控制器的收敛速度更快。但是,本文仅在仿真环境探究了机械臂控制算法的有效性,还存在一定的局限性,未来需要在实际工程任务中进行验证。