飞机进近阶段的接收机自主完好性监测研究综述

刘磊磊,张鹏飞,马振华,何 印,冀云彪

(中北大学 航空宇航学院,山西 太原 030051)

0 引 言

随着全球导航卫星系统(Global Navigation Satellite System,GNSS)的全面发展和完善,GNSS在世界范围内得到了广泛的应用[1]。GNSS作为一种具有全球性、全天候、高精度、高可靠性等优势的卫星导航系统,在民用航空中也发挥着越来越重要的作用。GNSS应用于民航领域具有导航精度高、空域利用率高、全球覆盖、运行成本低等优点。传统的陆基无线电导航的定位误差随着航空器与导航设备之间距离的增加而增大,相比较而言,目前GNSS的定位精度已经达到较高水平。以北斗卫星导航系统(BDS)为例,在全球范围内水平方向平均定位精度≤9 m,垂直方向平均定位精度≤10 m,在实际应用中达到的定位精度会更高。同时,GNSS用于飞机进近阶段导航还可以有效减少陆基导航设施,节约运行成本,提高运行效率,增加飞行流量。

近年来,随着经济的高速发展,航空领域呈现出繁荣景象。在2019年,全球平均每天有120 000个可靠性航班,从2019年到2038年,全球民航市场需要增加约39 000架民航飞机[2]。保障航空安全运行的关键技术之一是稳定、可靠的进近技术,这就需要对GNSS用于飞机进近导航的精度和完好性提出更高的要求。为此,许多国家通过增加卫星个数、利用新的完好性验证信息来提高GNSS的可靠性,提升其应对风险的能力[3]。提供可靠的完好性服务是通过完好性监测来实现的,完好性主要是保证系统提供定位服务的品质,完好性监测主要对系统存在影响定位精度的故障进行有效检测和排除。GNSS三级完好性监测的分类如图1 所示。

图1 中,接收机自主完好性监测(Receiver Autonomous Integrity Monitoring,RAIM)是利用冗余信息进行故障的检测、识别和排除,并及时向用户发出告警[4]。就目前导航现状以及未来多系统组合导航的背景而言,用户获得的观测量不断增加,新增的多频信号恰好可以消除电离层延迟,解决了对完好性最大的威胁,同时,RAIM技术不需要外部设施,并具有快速、方便、成本低的优势,所以采用RAIM技术可以提高GNSS在民航导航中的完好性,从而实现实时的完好性监测和进场服务[5]。

1 飞机进近阶段对GNSS的完好性要求

飞机在到达机场后的最后飞行阶段称为进近阶段。传统的进近类型分为非精密进近(NPA)和精密进近(PA)两种,NPA只提供水平方向引导的进近程序,PA不仅能提供水平方向引导的进近程序,还可以提供垂直方向引导的进近程序[6]。飞机进近阶段的划分情况如图2 所示,精密进近又可划分为APV-Ⅰ、APV-Ⅱ和CAT 三个阶段[7]。

图2 飞机进近阶段

根据国际民航组织(International Civil Aviation Organization,ICAO)中的规定,民航进近过程中不同飞行阶段的完好性性能要求如表1 所示,分别从水平和垂直精度、水平和垂直告警极限、完好性、告警时间、连续性和可用性来体现不同飞行阶段的性能要求。

飞机进近阶段的导航性能要求主要从精度、完好性、可用性和连续性四个方面进行评估。在保证精度的基础上,满足连续性和完好性的要求,才能保证服务的可用性。为了确保安全可靠,需要在规定时间内完成对故障的检测和识别,并及时排除故障。在导航性能需求中,完好性风险、连续性风险、误警率、漏检率、告警门限和告警时间也是非常重要的指标。连续性风险和完好性风险分别对应误警率和漏检率,且两者只能在允许的范围内互相包容。告警门限表示系统所允许的最大偏差限值范围,如果故障偏差超过告警门限,系统就会向用户发出告警,在非精密进近阶段只考虑水平告警门限,而在精密进近阶段还需考虑垂直告警门限。告警时间是指用户接收到报警的时间与用户误差超过限值的时间之差,表示系统所允许的最大报警时间。故障检测分布如图3 所示。

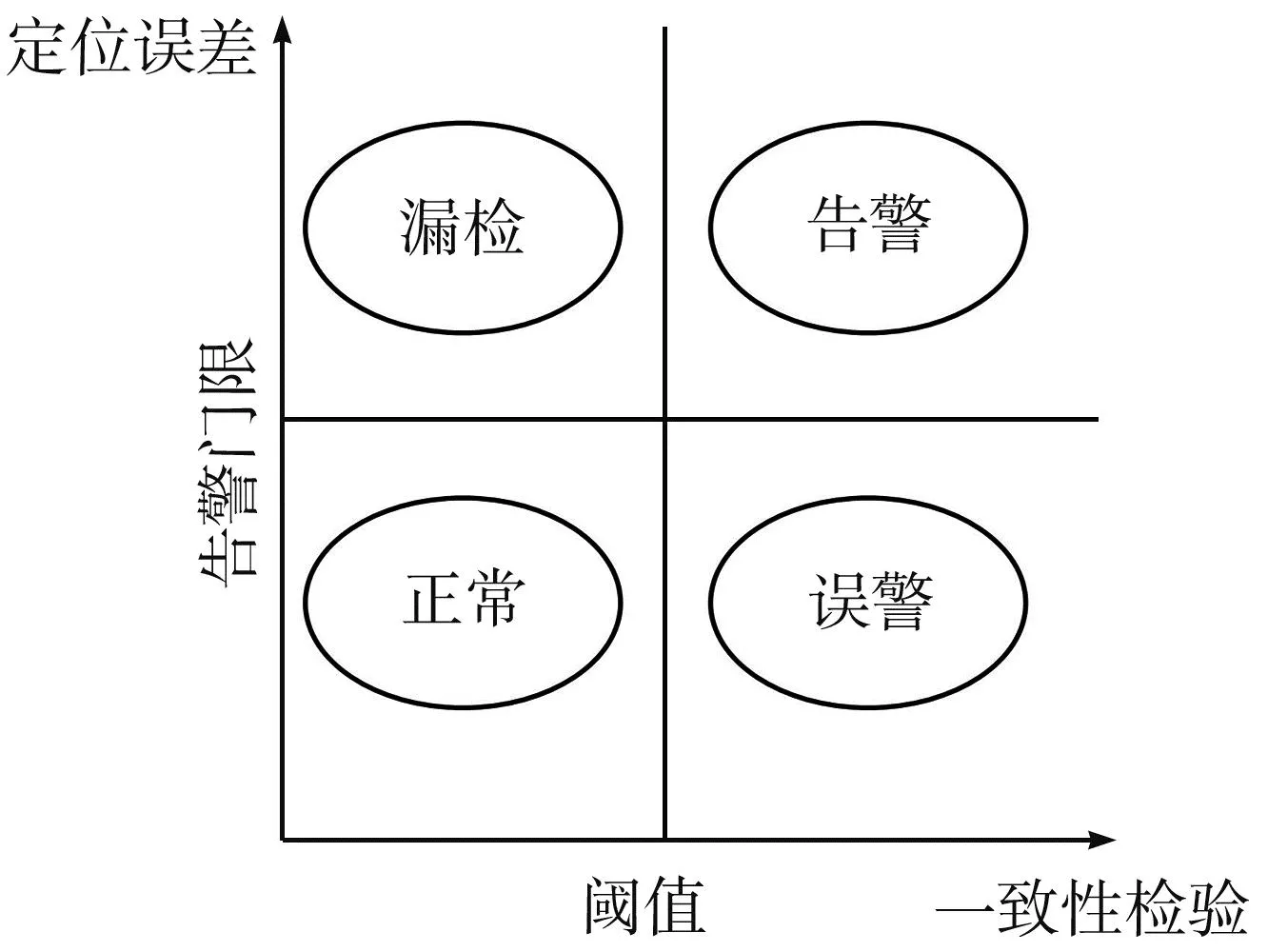
图3 故障检测分布图

当定位误差超过告警门限且一致性检验超过阈值时,就会告警; 仅定位误差超过告警门限,则是漏检; 仅一致性检验超过阈值,则是误警; 两者都没有超过的属于正常。飞机精密进近阶段不仅要保证安全性和可靠性,而且对定位保护限值和告警时间要有更加严格的要求[9]。

2 飞机进近阶段RAIM算法的研究现状

2.1 RAIM算法发展及其分类

RAIM算法流程如图4 所示,图中,n表示可见卫星数,N表示进行故障检测的最小卫星数。首先进行RAIM的可用性判断,再进行故障的检测和排除,最后输出导航结果。RAIM是一种用户终端的自主完好性监测方法,主要研究内容包括两方面,一方面是故障的检测和识别算法[10-16],另一方面是RAIM可用性的判定方法。在自主完好性监测时,不仅要能进行定位解算和保护限值计算等,还要在其出现故障时能做出及时有效的报警。故障处理的目的是在有故障的情况下,仍可以进行导航服务,保证系统的可用性和连续性[17]。

图4 RAIM算法流程图[4]

GPS系统的操控部分本身具有卫星监测故障的功能,但是其故障告警的时间太长,不能满足航空导航中实时性的要求。因此,Lee提出了伪距比较法[18],通过冗余观测数据判断出错误的伪距测量值; Mkalafus提出在用户端进行卫星故障的检测,利用导航解算对存在故障的卫星进行排除[19]; Sturza[20]提出了奇偶矢量法,不仅对观测矩阵进行了QR分解,还在故障检测时将噪声误差也转换到了奇偶空间; Parkinson等[21]提出了最小二乘残差法; Juang[22]和Jeon等[23]采用最小二乘残差法进行了故障的检测和识别,并指出最小奇异值和卫星故障有对应关系。RAIM算法认为保护限值计算与可视卫星的几何分布有一定关系。卫星的几何结构决定了DOP值,卫星几何构型的改变可以提高用户的测量精度。

RAIM算法分为快照式RAIM算法和滤波式RAIM算法。快照式RAIM算法主要有最小二乘残差法、奇偶矢量法和伪距比较法等,这些方法都是基于连续性的RAIM算法,并且都是基于观测噪声服从高斯分布假设前提的。其中,伪距比较法、最小二乘残差法和奇偶矢量法对单故障的假设和服从高斯分布的噪声都有较好的检测效果,并且具有等效性[24]。滤波式RAIM算法主要有卡尔曼滤波算法、扩展卡尔曼滤波算法和粒子滤波算法等,这些算法都是基于离散型的RAIM算法。其中,粒子滤波算法可以解决观测噪声服从非高斯分布情况的故障检测。不论是快照式算法还是滤波式算法,都可以对单卫星或多卫星的故障进行检测。

2.2 快照式RAIM算法

目前,快照式RAIM算法主要以奇偶矢量法和最小二乘法为主,两种方法是等价的,只是表达形式不同。同时,最小二乘残差矢量是由多个矩阵相乘,而奇偶空间矢量是直接将观测矩阵QR分解,再进行相乘,所以在相同条件下,奇偶矢量法计算量小,速度也快,更适用于实际应用。奇偶矢量法的RAIM算法如图5 所示,该方法先通过卫星数和HPL来判断RAIM是否可用,然后通过构建奇偶矢量来计算检测统计量和门限,并根据两者的比较结果来进行故障识别,最后进行导航解算。

图5 奇偶矢量RAIM算法流程图

Zhang等[16]提出的奇偶矢量法只用于非精密进近和航路阶段。陈金平[19]提出改进的奇偶矢量法可以对两颗故障卫星进行检测,在计算量减少90%的同时,识别率能达到90%以上。周飞[25]采用奇偶矢量法对故障模型进行了研究,根据统计量和门限对单故障和多故障进行检测和识别,通过监测信号的完好性来提高定位可信度。王文博等[26]采用奇偶矢量法对BDS/GPS在几何精度因子、故障检测率、故障识别率等方面的性能进行了研究,结果表明BDS/GPS多星座融合导航系统在接收机自主完好性监测性能方面具有明显的优势。代长勇等[27]提出了新的加权奇偶矢量RAIM算法,该算法通过对各系统间测距均方根误差进行归一化处理,大大提高了多系统卫星导航接收机RAIM算法对测距均方根误差较小卫星的敏感度。朱祺等[28]对奇偶矢量法在进近阶段的可用性进行了分析,考虑到相邻时刻的量测噪声具有独立性[29],累加的奇偶矢量法是将相邻时刻的奇偶矢量进行累加优化后作为故障检测量,从而提高了该方法的微小故障检测能力。加权的奇偶矢量法具有更快的故障检测速度,从而明显减少了故障检测的响应时间,显著提高了RAIM的告警时间。综上所述,奇偶矢量法可以检测出微小故障和突变故障,提升检测速度,缩短告警时间,提高定位精度,以及提高精密进近阶段RAIM算法的可用性。

2.3 滤波式RAIM算法

大多数快照式RAIM算法都是利用冗余观测来进行一致性检验和故障排除[30-31],不需要借助外部设备,容易实现,但要求可见卫星不少于5颗,在可视卫星数少或存在多个故障时,无法进行故障检测,并且对于微小缓变故障的检测能力较差,从而导致系统的可靠性和精度降低[32]。微小故障检测功能的不足严重影响了RAIM在精密进近的可用性,因此,相关学者又提出了滤波式RAIM算法,这种算法不仅提高了对微小缓变故障的检测能力,使系统的定位精度更高,而且可以进行多故障检测,使系统更具有稳健性[33]。目前常用的典型滤波算法是卡尔曼滤波(Kalman Filter,KF)算法和粒子滤波(Particle Filter,PF)算法。

2.3.1 卡尔曼滤波算法

滤波式RAIM算法主要利用前一时刻和当前时刻的信息来降低测量噪声水平[34]。Harsha[35]、沙海[36]等在此基础上提出了基于卡尔曼滤波的RAIM算法,提高了故障检测性能,但其前提是需假设观测噪声服从高斯分布,否则会影响RAIM的可用性[37-38]。

在动态数据处理中,卡尔曼滤波理论作为一种重要的最优估计得到了广泛应用。卡尔曼滤波是一种线性的最小方差估计,估计值是观测量的线性函数[39],它的估计误差最小且为无偏估计。卡尔曼滤波用递推的方法减少了计算量,而且是利用状态空间在时域内进行设计,因此适用于多维随机过程。卡尔曼滤波的RAIM算法流程如图6 所示,其先通过K-1时刻的状态量来预测K时刻的状态量和观测量,然后确定方差以计算统计检测量和门限值,再通过两者的比较结果进行故障识别。

图6 基于卡尔曼滤波的RAIM算法流程图

周富相等[40]中基于卡尔曼滤波的RAIM算法能够对多故障进行检测和识别,且可以有效降低漏检率和误警率。吴瑀[41]在扩展卡尔曼滤波(Extended Kalman Filter,EKF)的基础上提出了一种基于EKF的新息累加RAIM算法,分别给出了单卫星和双卫星的故障检测算法,仿真结果表明该算法对阶跃故障和微小故障均有较好的检测效果,可以准确找出卫星故障。杨瑛琳[42]提出了基于容积卡尔曼滤波(Cubature Kalman Filter,CKF)的RAIM方法,针对NPA阶段的RAIM可用性进行了仿真分析,结果表明其可用性得到了明显提升。陈宝远等[43]中提出的改进卡尔曼滤波算法对于检测的稳定性和精度都有一定程度的提高。综上所述,卡尔曼滤波算法可以更好地检测微小故障,提高RAIM算法的可用性,并且具有告警时间短、运算量小的特点,这对于改进精密进近的导航具有重要意义。

2.3.2 粒子滤波算法

EKF无法解决非线性、非高斯系统的状态估计问题[44],而且在飞机进行幅度较大的机动或者信号被干扰及遮挡时,观测误差并不服从高斯分布,这时采用EKF会导致检测精度降低。PF算法结合了蒙特卡洛方法与递推贝叶斯估计,通过粒子加权拟合系统状态的后验分布,适用于非线性、非高斯系统。因此,基于PF的RAIM算法逐渐成为学者研究的重点,但PF本身也存在粒子退化、计算量大等缺点,一般通过选择合理的建议密度函数和优化重采样策略来解决[45]。在国外,Schwiegelshohn[46]、Tran[47]、Daneshyar[48]等都对算法进行了不同程度的改进,以此来改善粒子退化现象; 在国内,王尔申等也利用遗传算法和粒子群优化算法对其进行了改进[49-51],虽然提高了RAIM算法在非高斯下的检测性能,但也增加了算法的复杂程度。PF作为一种非线性滤波方法,在处理实际环境中的非高斯、非线性的滤波估计方面比卡尔曼滤波有极大的优势。基于PF的RAIM算法流程图如图7 所示。

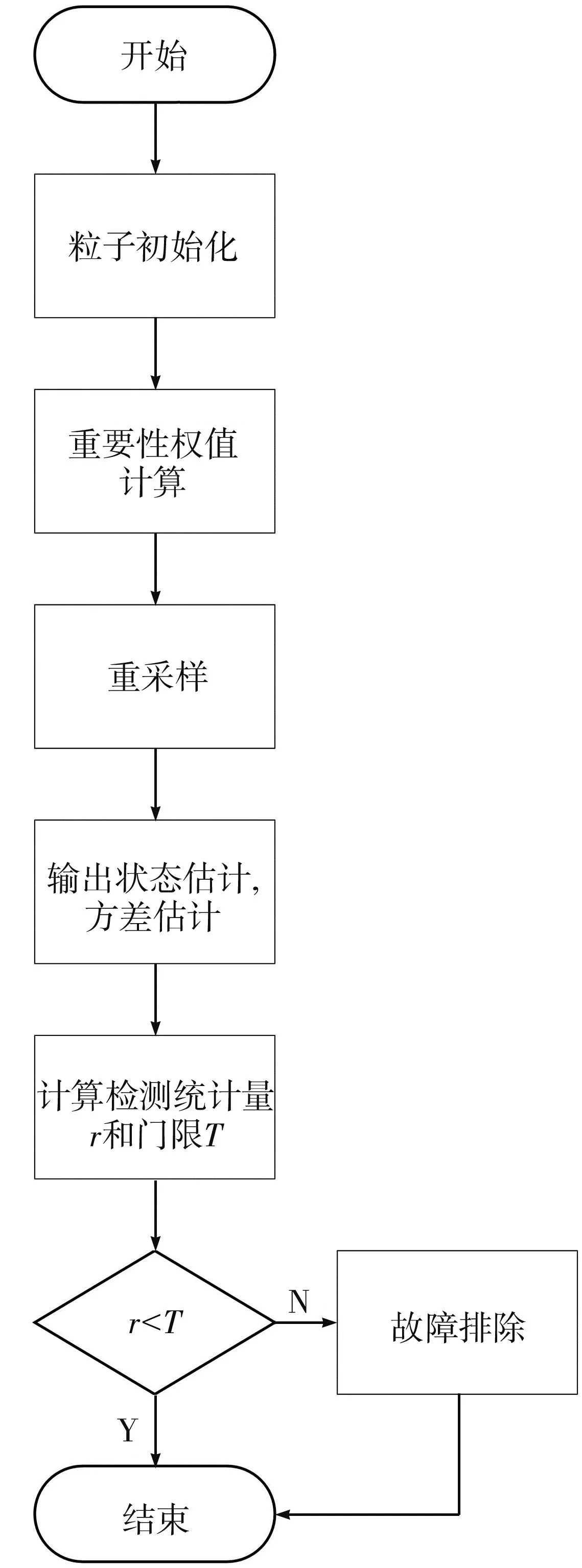
图7 基于粒子滤波的RAIM算法流程图

彭雅奇等[52]提出了基于鲁棒扩展卡尔曼粒子滤波(Robust Extended Kalman Particle Filter,REKPF)的RAIM算法,通过加入鲁棒估计的扩展卡尔曼滤波方法计算粒子的建议密度函数,提高了PF的估计精度,同时结合累加对数似然比来对故障卫星进行检测。仿真结果表明,基于REKPF的RAIM算法不但有效改善了粒子退化现象,而且提高了定位精度。贾超颖[53]将混沌粒子群优化算法(Chaotic Particle Swarm Optimization,CPSO)引入粒子滤波RAIM算法中,提出了基于CPSO的粒子滤波算法,通过建立PF-RAIM算法的状态空间模型,将CPSO与PF算法相结合,优化了粒子采样过程,实验结果表明,基于CPSO-PF的RAIM算法可以有效检测出阶跃偏差,对微小偏差故障也具有更好的检测性能,而且检测故障所需的时间更短,因此对于完好性检测具有很好的可用性和有效性。总之,基于非线性、非高斯的粒子滤波应用范围更广,在精密进近阶段,尤其是在CAT阶段,基于PF的RAIM算法的研究价值更高。

2.4 扩展RAIM算法

由于伪距观测值的噪声水平较大,因此基于伪距的RAIM算法的应用受到了很大限制,CRAIM(Carrier-phase RAIM)算法也就应运而生。CRAIM算法,即基于载波的RAIM算法,目前在飞机进近阶段有着广泛的应用。近年来,CRAIM算法得到了一定的发展,其按照定位模式可分为PTK-CRAIM算法、PPP-CRAIM算法、相对RAIM(RRAIM)算法等。CRAIM算法与RAIM算法比较,也存在着以下问题:1) 如何正确处理双差观测值之间的相关性; 2) 模糊度的确定问题; 3) 保护水平和完好性风险的优化配置问题。

随着GNSS星座的增加以及多频技术的发展,利用接收机自主完好性监测实现垂直导航成为可能,高级接收机完好性监测(Advanced Receiver Autonomous Integrity,ARAIM)因其在垂直导航方面的能力而具有明显的优势。ARAIM技术是指利用双频技术,通过多星座或者卫星接收机的冗余信息实现一致性监测,能够利用尽可能少的地面基础设施实现全球范围内空中无缝导航的目的,是RAIM方法的改进与扩展。ARAIM算法相较于RAIM算法可以在进近阶段为飞机提供垂直方向的完好性监测服务。现有的ARAIM算法主要包括多假设分组法(Multiple Hypothesis Separation Solution,MHSS)、最优加权平均解(Optimally Weighted Average Solution,OWAS)、新颖的完好性优化算法(Novel Integrity Optimized RAIM,NIORAIM)和卡方检验法。

目前,ARAIM的研究主要集中在三个方面:1) 故障检测。各种ARAIM算法中的故障类型多种多样,无法统一,一般把这些故障类型分为单故障、多故障和宽故障。对多故障和宽故障的检测与排除需要大量的研究和探索。2) ISM参数的生成与评估。国内外都在积极探索各星座的空间信号误差特性、先验故障概率、标称偏置等内容,以求尽快确定适用于各星座的ISM参数计算方法和评估标准[54]。3) ARAIM可用性。主要通过最优危险误导信息、误警率和完善ISM参数值来提高ARAIM的可用性[55]。

3 飞机进近阶段RAIM可用性方法的研究现状

3.1 RAIM可用性判定方法

在民航运行中,RAIM可用性预测的是飞机所在的位置,并且根据其位置来选择合理的可见卫星布局,并估计伪距测量误差,以检测RAIM算法的可用性。RAIM可用性算法不同于RAIM算法,RAIM算法是在用户接收机内部构建的,而RAIM可用性算法可以在任何第三方计算机上搭建,方便灵活。在对RAIM可用性判定时,还需要对卫星的可见数和布局情况进行分析[53]。在飞机精密进近阶段,RAIM可用性主要通过水平保护限值(HPL)和垂直保护限值(VPL)来判定[17]。对于接收机来说,每一颗可见卫星都有唯一的特征斜率与之对应,其中特征斜率是指定位误差与检测统计量的比值。几种经典的RAIM可用性判定方法如表2 所示,它们都是对最大斜率概念的延伸[18]。

3.2 单系统与多系统组合的RAIM可用性分析现状

随着全球四大卫星导航系统(GPS、GLONASS、BDS、Galileo)的建设,单系统导航在非精密进近阶段具有较高的可用性,但在精密进近阶段可用性明显不足,因此多系统导航成为了未来发展的趋势。近年来,国内外学者对GPS、GLONASS、BDS、Galileo多系统组合的RAIM进行了大量的研究[60-65]。

1) 单系统可用性:蒋虎等[17]利用GPS、GLONASS实际星历和BDS、Galileo仿真数据对APV-Ⅰ阶段RAIM的可用性进行了仿真分析,结果表明BDS单系统导航能满足亚洲、非洲和欧洲大部分地区的RAIM性能需求。焦卫东等[66]采用BDS和GPS的星历数据,利用加权的方法对APV-Ⅰ阶段RAIM的可用性进行了分析,结果表明,单一的BDS和GPS的可用性都超过了90%,但是不能完全满足其导航性能要求。陈雪[4]采用STK仿真卫星数据,对BDS单系统在LPV-200(决断高度为高于地面200 ft(即60.96 m))飞行阶段的RAIM可用性随用户位置变化的情况进行了仿真分析,结果表明,在西部地区,RAIM可用性不理想。

2) 双系统可用性:Ene等研究了Galileo、GPS双系统组合在垂直方向引导的进近阶段的RAIM可用性[61]。Martineau等对Galileo、GPS组合RAIM的截止高度角、用户等效距离误差、地表格网分辨率等进行了研究[62]。蒋虎等[17]分析了全球范围内不同双系统组合下的RAIM在APV-Ⅱ阶段的可用性,可用性结果差异较大,同时,用户可以在不同的位置选择不同的组合导航方式; 在CAT-Ⅰ阶段,双系统组合导航已经很难满足全球RAIM可用性要求,但BDS系统的加入可以使亚洲、非洲和欧洲部分区域的可用性达到99.0%以上。焦卫东等[66]利用BDS和GPS的星历数据,分别对其电离层模型的延迟进行了修正,还分析了对我国华北、华中和西部地区RAIM可用性的影响。在APV-Ⅰ阶段,基于卫星星座加权方法并在组合情况下,RAIM的可用性达到了100%,满足其性能要求; 在基于卫星类型加权方法的情况下,组合导航垂直方向的RAIM可用性为100%,满足其要求。

3) 三系统可用性:Hewitson等[64]对Galileo、GPS和GLONASS三系统组合RAIM在APV-Ⅰ、APV-Ⅱ阶段的可用性进行了分析。徐君毅等[65]推导了BDS与Galileo、GPS三系统组合导航PL的改善值,计算了精密进近阶段APV-Ⅰ、APV-Ⅱ的VPL在全球的分布。蒋虎等[17]比较了不同的三系统组合,结果表明,在APV-Ⅱ阶段GPS/Galileo/BDS三系统组合导航的RAIM可用性最高,且在全球陆地几乎都能达到99.5%以上,绝大部分区域可达到100%。

4)四系统可用性:蒋虎等[17]得出四系统在CAT-Ⅰ阶段的全球RAIM可用性达到100%。

综上所述,目前大多数研究主要是针对双系统和三系统组合导航,且大部分是对APV-Ⅰ、APV-Ⅱ两个阶段的分析,对于要求更高的CAT阶段几乎没有涉及。但是,随着我国BDS的全球组网,BDS和其他导航系统的组合导航将会发挥更大的作用,将会为精密进近阶段的导航开辟新篇章。

4 总结与展望

我国民航自“十一五”规划以来,基础设施和保障能力有了很大的提升,航空运输的能力也不断提高,航班数量不断增加,对于导航技术的要求也越来越严格,而当今以GNSS作为主要的导航方式,那么对于RAIM的研究就显得十分重要。本文对进近阶段的完好性要求进行了介绍,对RAIM算法的发展现状进行了分析,并按照RAIM算法的发展历程对不同的RAIM算法进行详细总结,最后介绍了三种不同的RAIM可用性判定方法,对单系统和多系统的RAIM在飞机进近阶段的可用性进行了综述,发现RAIM在APV-Ⅰ、APV-Ⅱ这两个阶段的可用性相对较高,但对于更高要求的CAT阶段,可用性明显不足,难以满足规定的要求。目前的RAIM还存在以下几个问题:

1) 实际的系统观测模型是非线性的,且实际观测噪声大都不服从高斯分布,传统的基于高斯分布假设的RAIM方法仅限于大陆航海、洋区航路以及非精密阶段[67],并不能很好地满足精密进近阶段的需求。

2) 从故障的检测识别到排除,冗余的方法对卫星数量有着严格的要求,在遮挡条件下可见卫星数量不足,导致RAIM算法的可用性降低。

3) 对于多星座多故障兼容的ARAIM算法还不够完善,解决其初始化漏检还需要进行深入探讨和研究。

GNSS导航作为一种航空导航方式,目前RAIM还不能完全为其提供满足需求的完好性监测[68],对于RAIM的研究今后将会重点集中在以下几方面:

1) 基于概率论和数理统计的概率方法在RAIM中的应用。用数理统计将RAIM算法转变为概率极限算法,以此来实现故障检测,可以降低误警率,并提供完好的可靠性服务。

2) 多系统组合的RAIM算法会越来越成熟,单系统RAIM算法已然满足不了现在的导航要求,特别是在CAT阶段。使用ARAIM时实际面对的故障模式也会增加,同时,随着可见星数量的增加,计算量大幅增加。因此,如何减少ARAIM的计算量也是急需解决的问题。

3) 对于多星故障问题,一些新算法有更好的故障检测与识别能力,未来对于多星座多故障的研究会得到改善,定位精度也会随之得到提升。

4) 基于外部手段辅助的RAIM检测方法会越来越多。基于外部手段辅助RAIM可以利用更少的可见卫星实现故障检测,定位精度也能满足需求,同时也能实现完好性与系统告警时间的平衡,使GNSS具有更好的导航能力。