基于真实运动轨迹螺旋立铣刀铣削力建模

叶子银, 李 军, 包虎子, 张锦淇, 俞弘宇

长安大学工程机械学院, 陕西 西安 710000

0 引言

铣削是一个周期性断续切削的过程,铣削力大小与未变形切屑厚度呈正相关[1]。因此,铣削过程中,随着刀具的运动,瞬时未变形切屑厚度发生变化,铣削力也相应变化。实践表明,动态变化的铣削力,将使切削过程中刀具和工件发生颤振[2],导致刀具磨损的加剧以及发生让刀或过切的情况,最终影响工件加工质量[3]。在实际加工中,特别是加工薄壁零件时,为降低颤振影响,保证加工质量,往往选择保守的切削参数,这样导致机床和刀具的性能无法充分利用,加工工艺存在较大优化空间。因此,建立铣削力模型并预测铣削力大小,有利于颤振机理的研究及加工工艺的优化。

针对铣削力建模,国内外学者进行了大量研究[4],目前应用最为广泛的铣削力建模法是机械建模法。机械建模法采用微元思想,将铣刀刀刃沿轴向离散成一系列轴向等距微元切削刃,将每个微元切削刃近似看成直角或斜角切削,通过切削力系数与未变形切屑面积计算每个微元切削刃受力,最终迭加每个微元切削刃受力的矢量和得到铣刀受力总和[5]。机械建模法计算铣削力的一个关键点在于未变形切屑面积的计算。未变形切屑面积是切削宽度和未变形切屑厚度的乘积,切削宽度由微元切削刃的离散程度和刀具几何参数决定,是一个确定的量,而未变形切屑厚度由切削参数和刀具参数共同决定,是一个动态变化的量。目前计算未变形切屑厚度大多采用Martellotti[6]提出的传统的未变形切屑厚度计算模型,该模型在每齿进给量远小于刀具半径时可较好地近似。然而,随着微铣削技术的发展及各种复杂薄壁零件的设计,传统模型计算出来的未变形切屑厚度与实际相差较大,从而导致最终计算出的铣削力偏差也较大。为优化未变形切屑厚度计算方法,获得更为精确的铣削力模型。本文基于铣削力机械建模法,将刀刃沿轴向离散成一系列微元,根据微元实际运动轨迹建立每个微元运动轨迹方程,利用建立的轨迹方程分析同一高度下相邻两齿微元运动轨迹的几何关系,计算瞬时未变形切屑厚度,得到刀具与工件接触区域范围,然后带入铣削力模型中计算铣削力,最后分析建立的模型与传统模型计算铣削力的偏差。

1 螺旋立铣刀微元运动模型

1.1 坐标系定义

为表示微元瞬时运动位置,建立如图1所示的坐标系。

图1 螺旋立铣刀微元几何模型

1)刀具坐标系(OT-XTYTZT):ZT轴平行于刀具轴线;YT轴与刀具端面任意刀齿根部相切;XT轴由ZT轴和YT轴构成右手系确定。

2)工件坐标系(OW-XWYWZW):ZW轴与ZT轴平行;YW轴与YT轴反向平行;XW轴与XT轴平行。

1.2 微元在刀具坐标系下的运动模型

假设铣刀半径为R,刀齿数为Nf,与YT轴相切的刀齿为第1齿,规定沿逆时针方向刀齿依次为第2齿至第Nf齿。若第1齿沿顺时针方向旋转角度为θ,刀齿间距角为Øp,铣刀螺旋角为β,铣削深度为ap,刀齿轴向微元份数为q,刀齿微元高度为dz=ap/q,刀齿i上高度为z的第j个微元螺旋滞后角为ψ,则第i个刀齿,第j个微元相对于第1齿的角度位置可表示为:

Ø(i,j)=θ-ψ-(i-1)Øp

(1)

其中,

(2)

(3)

(4)

相对于刀具坐标系原点OT坐标可表示为:

(5)

1.3 微元在工件坐标系下的运动模型

假设刀具沿XW轴方向运动每齿进给量为fz,转速为n,沿YW轴方向间歇进给运动次数为m,间歇进给行距为ae。若初始时刻刀具坐标系原点相对于工件坐标系原点坐标为(X0,Y0),则刀具上任意微元相对于工件坐标系原点坐标可以表示为:

(6)

式中:Vf为沿XW轴方向运动的进给速度;t为刀具运动时间。分别可表示为:

(7)

(8)

2 铣削力建模

2.1 螺旋立铣刀动态铣削力模型

采用机械建模法计算铣削力,刀具微元受力可表示为切向力dFt、径向力dFr和轴向力dFa:

(9)

式中:Ktc、Krc和Kac分别为切向、径向、轴向切削力系数;Kte、Kre和Kae分别为切向、径向、轴向的切削力刃口系数;t(i,j)为未变形切屑厚度;ds为切削刃长度。切削力系数通过铣削力标定试验获得[7],而切削刃长度可表示为ds=dz/cos(β)。

将刀齿微元所受径向、切向、轴向力坐标变换到刀具坐标系下:

(10)

任一时刻,迭加每个微元受力矢量和,得到刀具所受铣削力:

(11)

2.2 未变形切屑厚度计算

传统未变形切屑厚度计算时假设刀具轨迹为圆,如图2所示。根据几何关系推导出未变形切屑厚度表达式为:

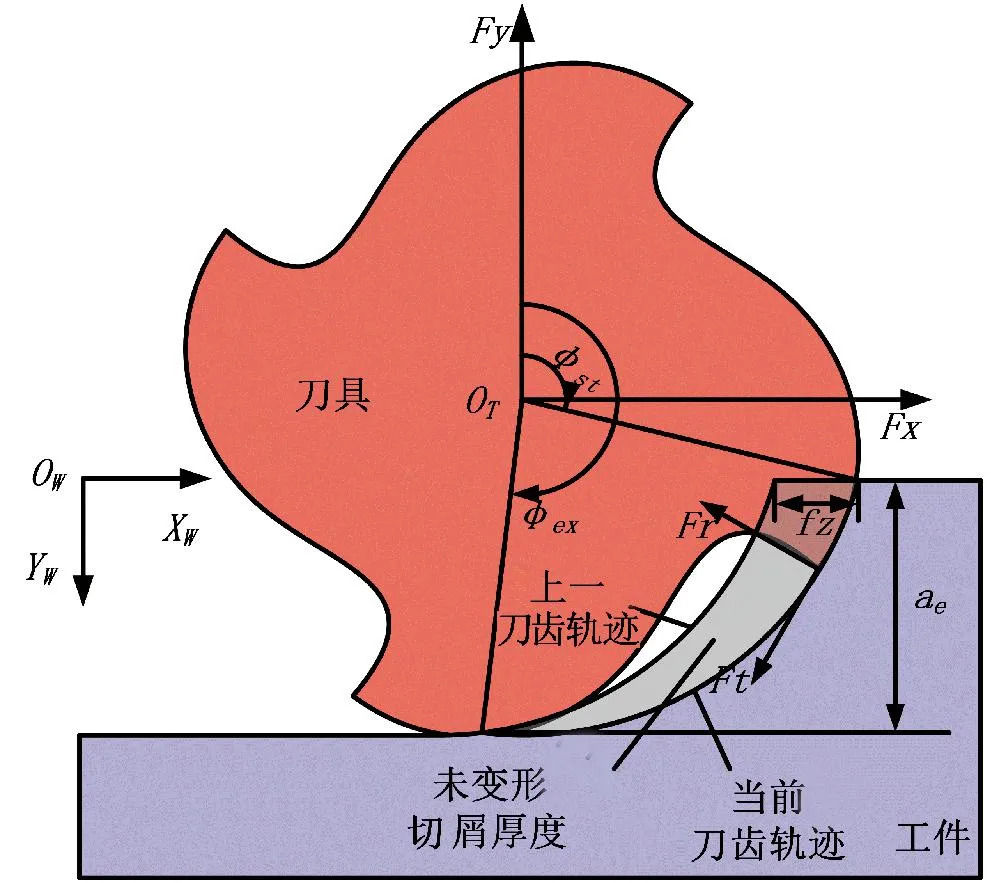
图2 传统未变形切屑厚度

t(i,j)=fzsin(Ø(i,j))

(12)

然而,在实际运动过程中,刀具轨迹并非为圆,而是一条次摆线,如图3所示。假设同一高度上第i-1个刀齿和第i个刀齿的第j个微元从初始时刻分别运动到A点和B点的时刻分别为ta和tb,则点A和点B在工件坐标系的位置为:

图3 真实轨迹未变形切屑厚度

(13)

(14)

刀具轴心在tb时刻相对工件坐标系的位置为:

(15)

根据几何关系可得O4A和O4B共线,建立以下方程。

(XWB(i,j)-XWO4(i,j))YWA-(XWA(i,j)-XWO4(i,j))YWB=0

(16)

联立式(13)～(16),采用Newton迭代法可求解该方程,将求得的解带入下式即可得到目前时刻的未变形切屑厚度。

(17)

2.3 刀具-工件接触区域确定

刀具运动过程中只有在切削区域才会参与切削,才能有铣削力,根据图3刀具轨迹可计算出刀具切削区域的切入角为:

(18)

切出角为:

(19)

3 模型仿真与对比

3.1 未变形切屑厚度仿真

为对比本文建立的模型与传统模型之间偏差,选择刀具半径为5 mm、刀具螺旋角为30°、刀齿数为2的刀具分别在每齿进给量为0.2 mm/r和0.5 mm/r条件下计算2种模型的未变形切屑厚度值,计算结果如图4所示。由图可知,随着每齿进给量的增加,传统模型相较于本文模型计算出的未变形切屑厚度值偏差越来越大,且总体上传统模型计算值偏小。

(a)每齿进给量为0.2 mm/r时

3.2 铣削力仿真

文献[8]对铝合金7050开展了铣削试验,其测得的铣削力数据可用于本文模型的验证。该试验在VMC0850B机床上进行,使用的刀具为公称直径12 mm刀齿数2的肯纳ABDF1200A2AS硬质合金刀具,采用的测力装置为Kistler9257三向测力仪。试验方案为固定主轴转速为4 000 r/min,切削宽度为12 mm,改变切削深度在0.5、1、1.5 mm变化以及进给速度在200、400、600 mm/min变化,组成2因素3水平正交试验。通过对试验测得的铣削力数据进行处理得到各切削力系数分别为:Ktc=1 037.35,Krc=216.01,Kac=-353.53,Kte=32.083,Kre=60.39,Kae=1.65。

基于上述求得的切削力系数,本文选择在切削深度为1.5 mm,进给速度为600 mm/min条件下仿真,结果如图5所示。由图5可知,在铣刀旋转前半周,本文所建模型得到的铣削力相较于传统模型计算出的铣削力更加接近试验值,而旋转后半周,2种模型计算的铣削力都与实际测量值相差较远。这可能是因为后半周切削时刀具颤振、磨损等因素导致实际切削厚度小于理论计算厚度,从而影响最终铣削力试验测量值偏离预测值。

图5 铣削力预测结果对比

4 结论

1)本文根据铣刀实际运动轨迹,建立了一种新的未变形切屑厚度计算模型。该模型与传统未变形切屑厚度计算模型相比,计算的未变形切屑厚度值总体大于传统模型计算的值。

2)采用相关文献铣削试验数据,比较本文所建模型与传统模型预测铣削力曲线,表明本文建立模型预测的铣削力更接近试验值。因此,本文所建模型预测铣削力拥有更高预测精度。